HOW THE ZEBRA GOT ITS STRIPES: THE MATHEMATICS OF PATTERN FORMATION

Undergraduate Mathematics Colloquium

 

10/28/2015

Chris Miles

PATTERNS

QUESTION:

Does a general theory exist describing the formation of patterns from non-patterns?

ALAN TURING

MORPHOGENESIS

  • biological process of organism developing its shape
     
  • all cells start from single precursor
     
  • incredibly complex!

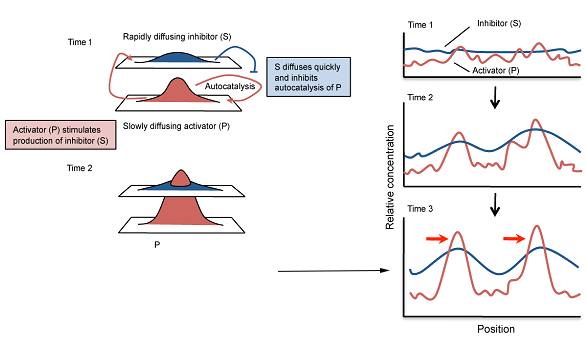
KEY COMPONENTS

local activation
long range inhibition

reaction = stuff interacting

 

 

diffusion = stuff moving around 

Turing instability: diffusion driven

 

without diffusion: no pattern (stable)

diffusion: pattern 

MORPHOGENS

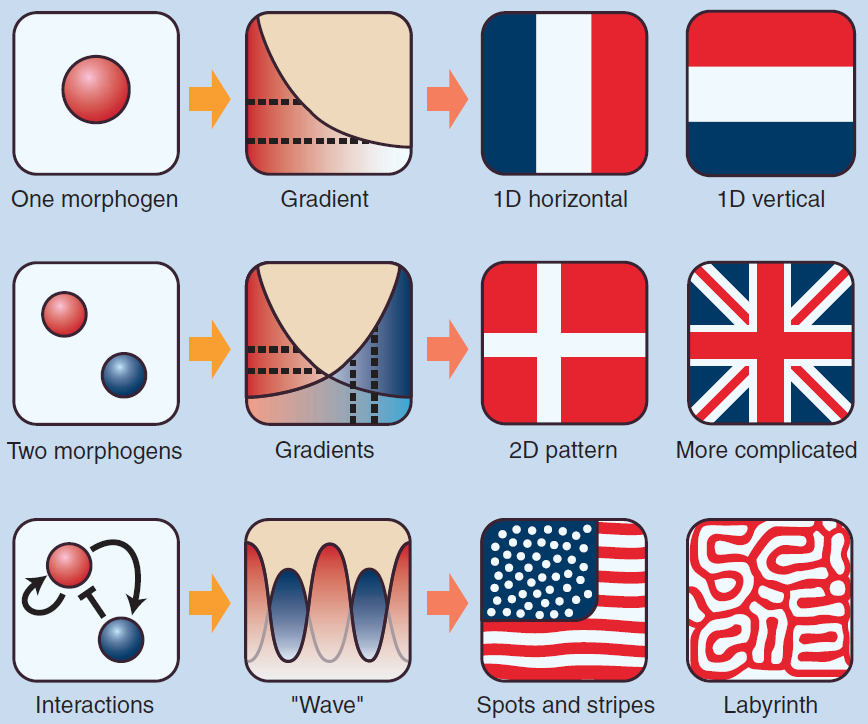
WAVE FORMATION

diffusion driven pattern!

MATHEMATICAL FORMATION

\frac{\partial u}{\partial t} = f(u,v) + D_u \frac{\partial^2 u}{\partial x^2}
∂u∂t=f(u,v)+Du∂2u∂x2\frac{\partial u}{\partial t} = f(u,v) + D_u \frac{\partial^2 u}{\partial x^2}

rate of change of chemical concentration

reactions

diffusion

\frac{\partial v}{\partial t} = g(u,v) + D_u \frac{\partial^2 v}{\partial x^2}
∂v∂t=g(u,v)+Du∂2v∂x2\frac{\partial v}{\partial t} = g(u,v) + D_u \frac{\partial^2 v}{\partial x^2}
u(x,t)
u(x,t)u(x,t)
v(x,t)
v(x,t)v(x,t)

= concentration of morpohgen at position x, time t

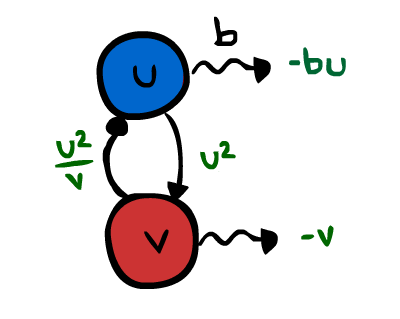
GIERER-MEINHARDT

\frac{\partial u}{\partial t} = \frac{ u^2}{v} - bu + D_u \frac{\partial^2u}{\partial x^2},
∂u∂t=u2v−bu+Du∂2u∂x2, \frac{\partial u}{\partial t} = \frac{ u^2}{v} - bu + D_u \frac{\partial^2u}{\partial x^2},

used to describe sea-shell patterns (1972)

\frac{\partial v}{\partial t} =u^2 - v + D_v \frac{\partial^2v}{\partial x^2}.
∂v∂t=u2−v+Dv∂2v∂x2. \frac{\partial v}{\partial t} =u^2 - v + D_v \frac{\partial^2v}{\partial x^2}.

STEADY STATE

With no diffusion:

\frac{\partial u}{\partial t} = \frac{ u^2}{v} - bu,
∂u∂t=u2v−bu, \frac{\partial u}{\partial t} = \frac{ u^2}{v} - bu,
\frac{\partial v}{\partial t} =u^2 - v.
∂v∂t=u2−v. \frac{\partial v}{\partial t} =u^2 - v.

Steady state:

0= \frac{ u^2}{v} - bu,
0=u2v−bu,0= \frac{ u^2}{v} - bu,
0=u^2 - v.
0=u2−v.0=u^2 - v.
(u_0, v_0) = (1/b, 1/b^2)
(u0,v0)=(1/b,1/b2)(u_0, v_0) = (1/b, 1/b^2)
D_u, D_v =0
Du,Dv=0D_u, D_v =0

LINEARIZATION

(u_0, v_0) = (1/b, 1/b^2)
(u0,v0)=(1/b,1/b2)(u_0, v_0) = (1/b, 1/b^2)

Perturb slightly from our steady state:

u(x,t) = u_0 + \tilde{u},
u(x,t)=u0+u~,u(x,t) = u_0 + \tilde{u},
v(x,t) = v_0 + \tilde{v}
v(x,t)=v0+v~v(x,t) = v_0 + \tilde{v}

Taylor expand around steady state:

f(u,v) = f(u_0, v_0) + \tilde{u}\frac{\partial f(u_0,v_0)}{\partial u} + \tilde{v}\frac{\partial f(u_0,v_0)}{\partial v} + ...
f(u,v)=f(u0,v0)+u~∂f(u0,v0)∂u+v~∂f(u0,v0)∂v+... f(u,v) = f(u_0, v_0) + \tilde{u}\frac{\partial f(u_0,v_0)}{\partial u} + \tilde{v}\frac{\partial f(u_0,v_0)}{\partial v} + ...
\frac{\partial}{\partial t} \binom{\tilde{u}}{ \tilde{v}} = \left(D\frac{\partial}{\partial x^2} + J \right) \binom{\tilde{u}}{\tilde{v}},
∂∂t(u~v~)=(D∂∂x2+J)(u~v~),\frac{\partial}{\partial t} \binom{\tilde{u}}{ \tilde{v}} = \left(D\frac{\partial}{\partial x^2} + J \right) \binom{\tilde{u}}{\tilde{v}},

Only take leading order terms:

J = \left( \begin{array}{cc} \partial f / \partial u & \partial f/ \partial v \\ \partial g/\partial u & \partial g / \partial v \end{array} \right)
J=(∂f/∂u∂f/∂v∂g/∂u∂g/∂v) J = \left( \begin{array}{cc} \partial f / \partial u & \partial f/ \partial v \\ \partial g/\partial u & \partial g / \partial v \end{array} \right)
D = \left( \begin{array}{cc} D_u & 0 \\ 0 & D_v \end{array} \right)
D=(Du00Dv) D = \left( \begin{array}{cc} D_u & 0 \\ 0 & D_v \end{array} \right)

STABLE STEADY STATE

diffusion driven = stable with no diffusion

\left.J\right|_{(1/b, 1/b^2)} = \left. \left(\begin{array}{cc} -b + \frac{2u}{v} & - \frac{u^2}{v^2} \\ 2u & -1 \end{array} \right) \right|_{(1/b, 1/b^2)} = \left(\begin{array}{cc} b & - b^2 \\ \frac{2}{b} & -1 \end{array} \right).
J∣(1/b,1/b2)=(−b+2uv−u2v22u−1)∣(1/b,1/b2)=(b−b22b−1).\left.J\right|_{(1/b, 1/b^2)} = \left. \left(\begin{array}{cc} -b + \frac{2u}{v} & - \frac{u^2}{v^2} \\ 2u & -1 \end{array} \right) \right|_{(1/b, 1/b^2)} = \left(\begin{array}{cc} b & - b^2 \\ \frac{2}{b} & -1 \end{array} \right).
\frac{\partial}{\partial t} \binom{\tilde{u}}{ \tilde{v}} =J \binom{\tilde{u}}{\tilde{v}},
∂∂t(u~v~)=J(u~v~),\frac{\partial}{\partial t} \binom{\tilde{u}}{ \tilde{v}} =J \binom{\tilde{u}}{\tilde{v}},

for Gierer-Meinhardt

result from ODE theory: solutions look like

\binom{\tilde{u}}{\tilde{v}} = e^{\lambda_1 t} a(x)+ e^{\lambda_2 t} b(x)
(u~v~)=eλ1ta(x)+eλ2tb(x)\binom{\tilde{u}}{\tilde{v}} = e^{\lambda_1 t} a(x)+ e^{\lambda_2 t} b(x)

are eigenvalues of 

\lambda_1, \lambda_2
λ1,λ2\lambda_1, \lambda_2
J
JJ
D_u, D_v =0
Du,Dv=0D_u, D_v =0

STABLE STEADY STATE

fact: 

e^{\lambda t} \to 0
eλt→0e^{\lambda t} \to 0
Re (\lambda) < 0
Re(λ)<0Re (\lambda) < 0

if

thus, this boils down to:

tr(J) = b-1 < 0
tr(J)=b−1<0tr(J) = b-1 < 0
det(J) = b >0
det(J)=b>0det(J) = b >0
0 < b < 1
0<b<10 < b < 1

DIFFUSION DRIVEN INSTABILITY

D_u, D_v \neq 0
Du,Dv≠0D_u, D_v \neq 0
u(x,t) = u_0 + \tilde{u},
u(x,t)=u0+u~,u(x,t) = u_0 + \tilde{u},
v(x,t) = v_0 + \tilde{v}
v(x,t)=v0+v~v(x,t) = v_0 + \tilde{v}
\frac{\partial \tilde{u}}{\partial t} = b\tilde{u} - b^2 \tilde{v}+ D_u \frac{\partial^2\tilde{u}}{\partial x^2},
∂u~∂t=bu~−b2v~+Du∂2u~∂x2,\frac{\partial \tilde{u}}{\partial t} = b\tilde{u} - b^2 \tilde{v}+ D_u \frac{\partial^2\tilde{u}}{\partial x^2},
\frac{\partial \tilde{v}}{\partial t} = \frac{2}{b} \tilde{u} - \tilde{v} + D_v \frac{\partial^2\tilde{v}}{\partial x^2}.
∂v~∂t=2bu~−v~+Dv∂2v~∂x2. \frac{\partial \tilde{v}}{\partial t} = \frac{2}{b} \tilde{u} - \tilde{v} + D_v \frac{\partial^2\tilde{v}}{\partial x^2}.
\binom{\tilde{u}}{\tilde{v}} =\binom{ A(t)e^{iqx} }{B(t)e^{iqx}}
(u~v~)=(A(t)eiqxB(t)eiqx) \binom{\tilde{u}}{\tilde{v}} =\binom{ A(t)e^{iqx} }{B(t)e^{iqx}}

Look for solutions of the form:

e^{iqx} = \cos(qx) + i \sin(qx)
eiqx=cos(qx)+isin(qx)e^{iqx} = \cos(qx) + i \sin(qx)

Euler's identity

waves!

\frac{\partial}{\partial t} \binom{\tilde{u}}{\tilde{v}} = \left( \begin{array}{cc} b - q^2D_u & -b^2 \\ \frac{2}{b} & -1-q^2D_v \end{array} \right) \binom{\tilde{u}}{\tilde{v}}
∂∂t(u~v~)=(b−q2Du−b22b−1−q2Dv)(u~v~)\frac{\partial}{\partial t} \binom{\tilde{u}}{\tilde{v}} = \left( \begin{array}{cc} b - q^2D_u & -b^2 \\ \frac{2}{b} & -1-q^2D_v \end{array} \right) \binom{\tilde{u}}{\tilde{v}}

DIFFUSION DRIVEN INSTABILITY

\frac{\partial}{\partial t} \binom{\tilde{u}}{\tilde{v}} = \left( \begin{array}{cc} b - q^2D_u & -b^2 \\ \frac{2}{b} & -1-q^2D_v \end{array} \right) \binom{\tilde{u}}{\tilde{v}}
∂∂t(u~v~)=(b−q2Du−b22b−1−q2Dv)(u~v~)\frac{\partial}{\partial t} \binom{\tilde{u}}{\tilde{v}} = \left( \begin{array}{cc} b - q^2D_u & -b^2 \\ \frac{2}{b} & -1-q^2D_v \end{array} \right) \binom{\tilde{u}}{\tilde{v}}

want INSTABILITY

tr(J) = b-1-q^2(D_u+D_v) <0
tr(J)=b−1−q2(Du+Dv)<0tr(J) = b-1-q^2(D_u+D_v) <0
b<1
b<1b<1
det(J) = (b-D_u q^2)(-1 - D_v q^2) < 0
det(J)=(b−Duq2)(−1−Dvq2)<0det(J) = (b-D_u q^2)(-1 - D_v q^2) < 0

always true since

PATTERN FORMATION

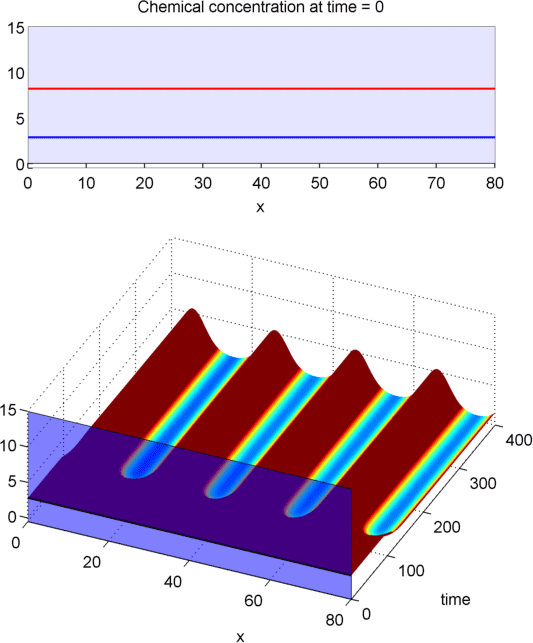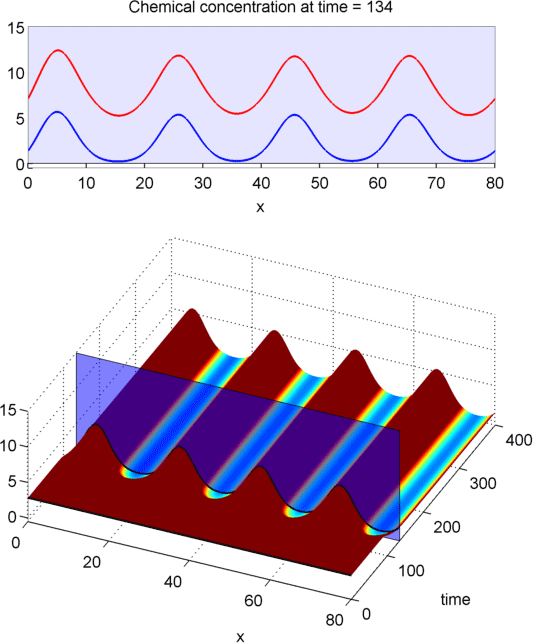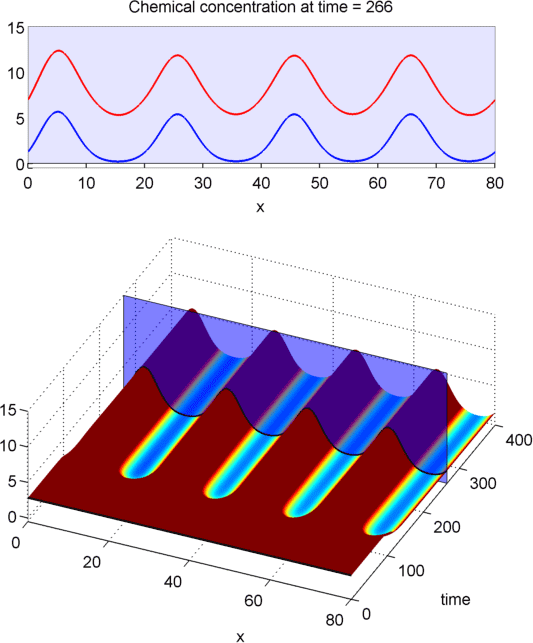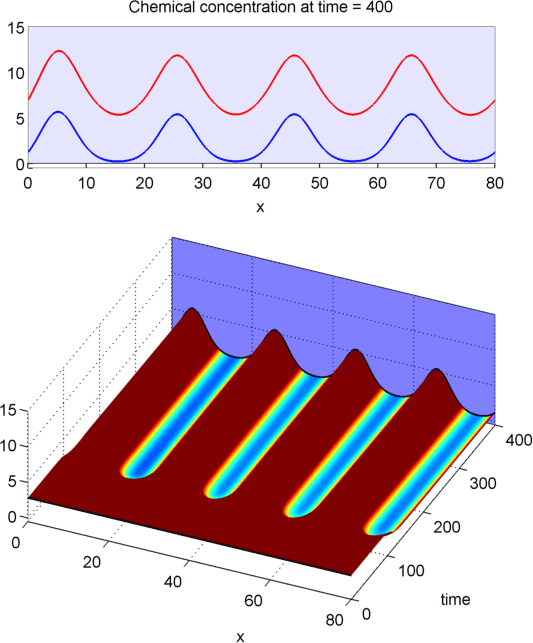
DOMAIN DEPENDENCE

What is q?

If our domain is [0,L], solutions look like:

\sum_{k} A_k e^{\lambda q^2 t} \cos (qx), \qquad q = \frac{n\pi}{L}
∑kAkeλq2tcos(qx),q=nπL\sum_{k} A_k e^{\lambda q^2 t} \cos (qx), \qquad q = \frac{n\pi}{L}

(from Fourier)

critical domain size!

INSUFFICIENT L

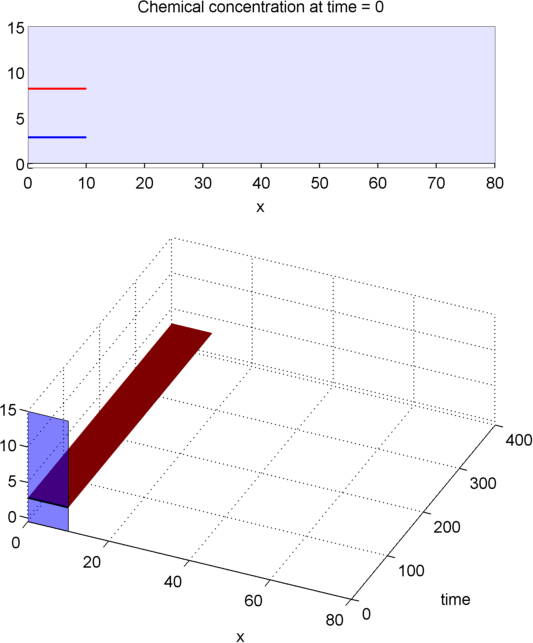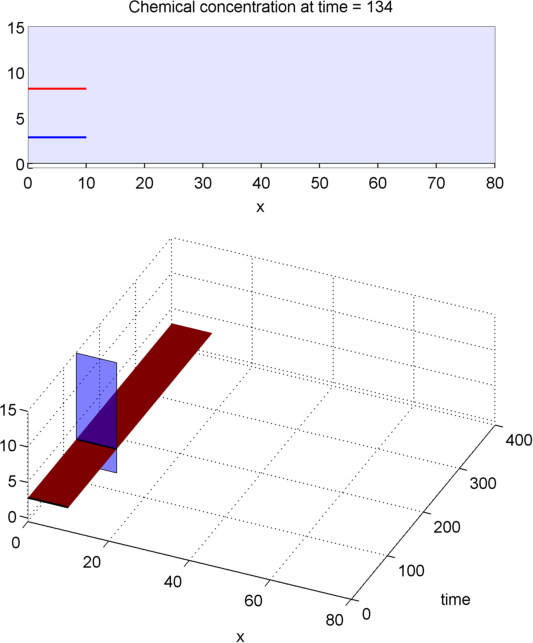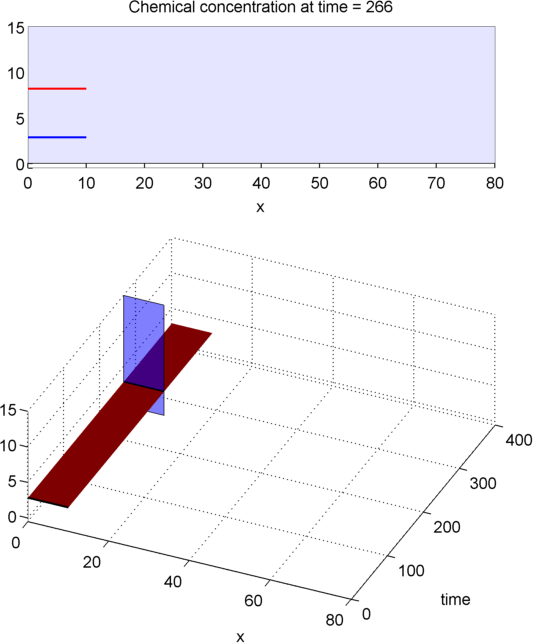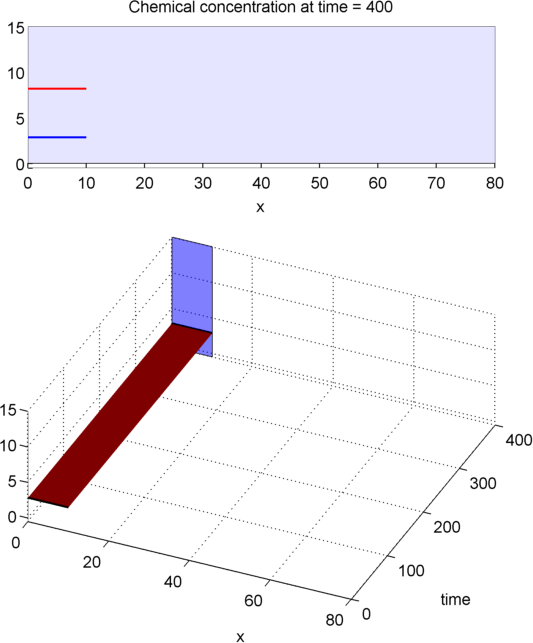
OTHER REACTIONS

\frac{\partial u}{\partial t} = D_u \Delta u - uv^2 +F(1-u),
∂u∂t=DuΔu−uv2+F(1−u), \frac{\partial u}{\partial t} = D_u \Delta u - uv^2 +F(1-u),
\frac{\partial v}{\partial t} = D_v \Delta u +uv^2-(F+c)v.
∂v∂t=DvΔu+uv2−(F+c)v. \frac{\partial v}{\partial t} = D_v \Delta u +uv^2-(F+c)v.

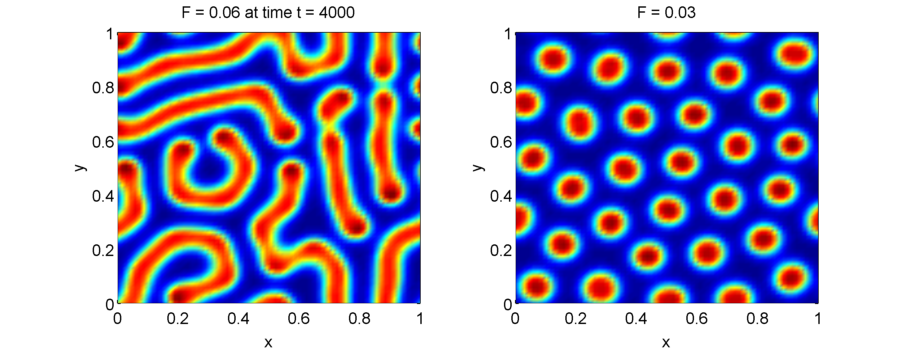
Gray-Scott:

\Delta u = \nabla^2 u = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}
Δu=∇2u=∂2u∂x2+∂2u∂y2\Delta u = \nabla^2 u = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}

OTHER DOMAINS

https://github.com/gollygang/ready

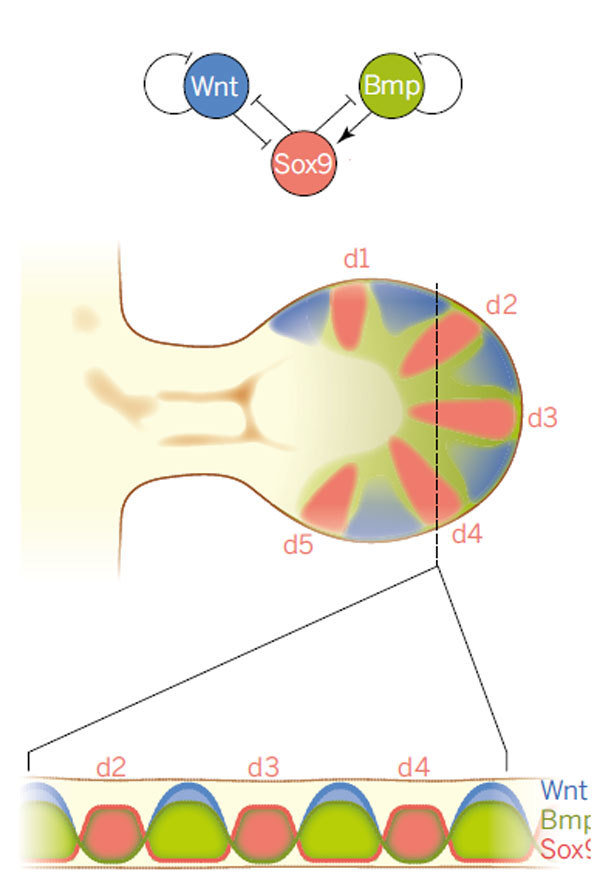
CURRENT RESEARCH

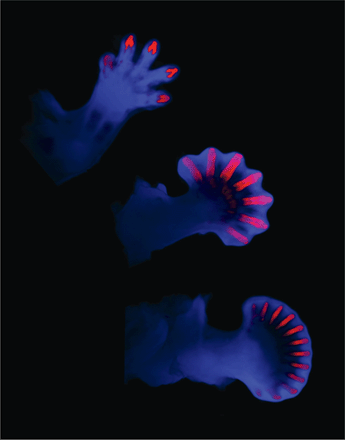
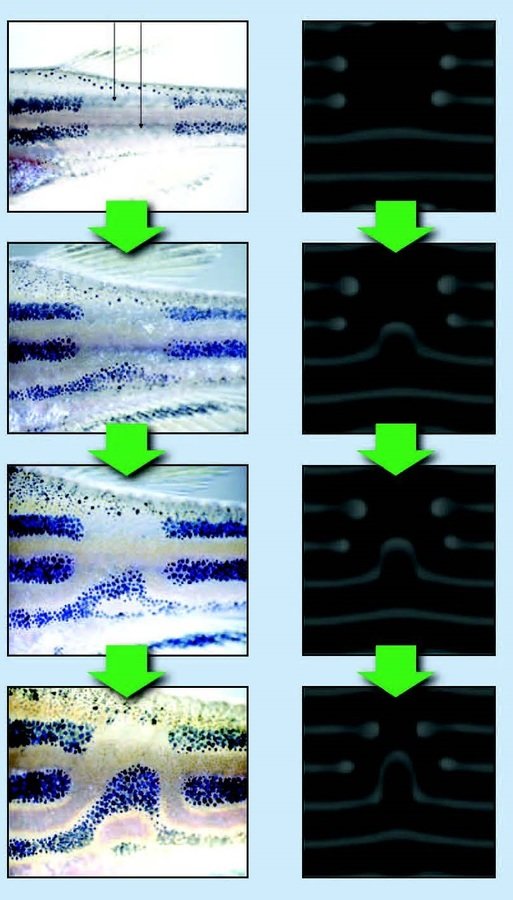
REFERENCES

  1. S. Kondo and T. Miura, “Reaction-diffusion model as a framework for understanding biological pattern formation,” Science, vol. 329, no. 5999, pp. 1616–1620, (2010). 
  2. http://www.theshapeofmath.com/princeton/dynsys
  3.  P.K. Maini, “The impact of Turing's work on pattern formation in biology,” Mathematics Today, 40(4), 140-141 (2004).
  4. “Theoretical aspects of pattern formation and neuronal development”, Hans Meinhardt

this presentation is on my website: http://chrismil.es

HOW THE ZEBRA GOT ITS STRIPES: MATHEMATICAL PATTERN FORMATION

By Chris Miles

Made with Slides.com

HOW THE ZEBRA GOT ITS STRIPES: MATHEMATICAL PATTERN FORMATION

A presentation for the undergraduate mathematics colloquium at the University of Utah on mathematical pattern formation and Turing instabilities.

  • 1,882

More from Chris Miles