Pentominoes,

Exact Covers, and Algorithm X

David Radcliffe

February 9, 2017

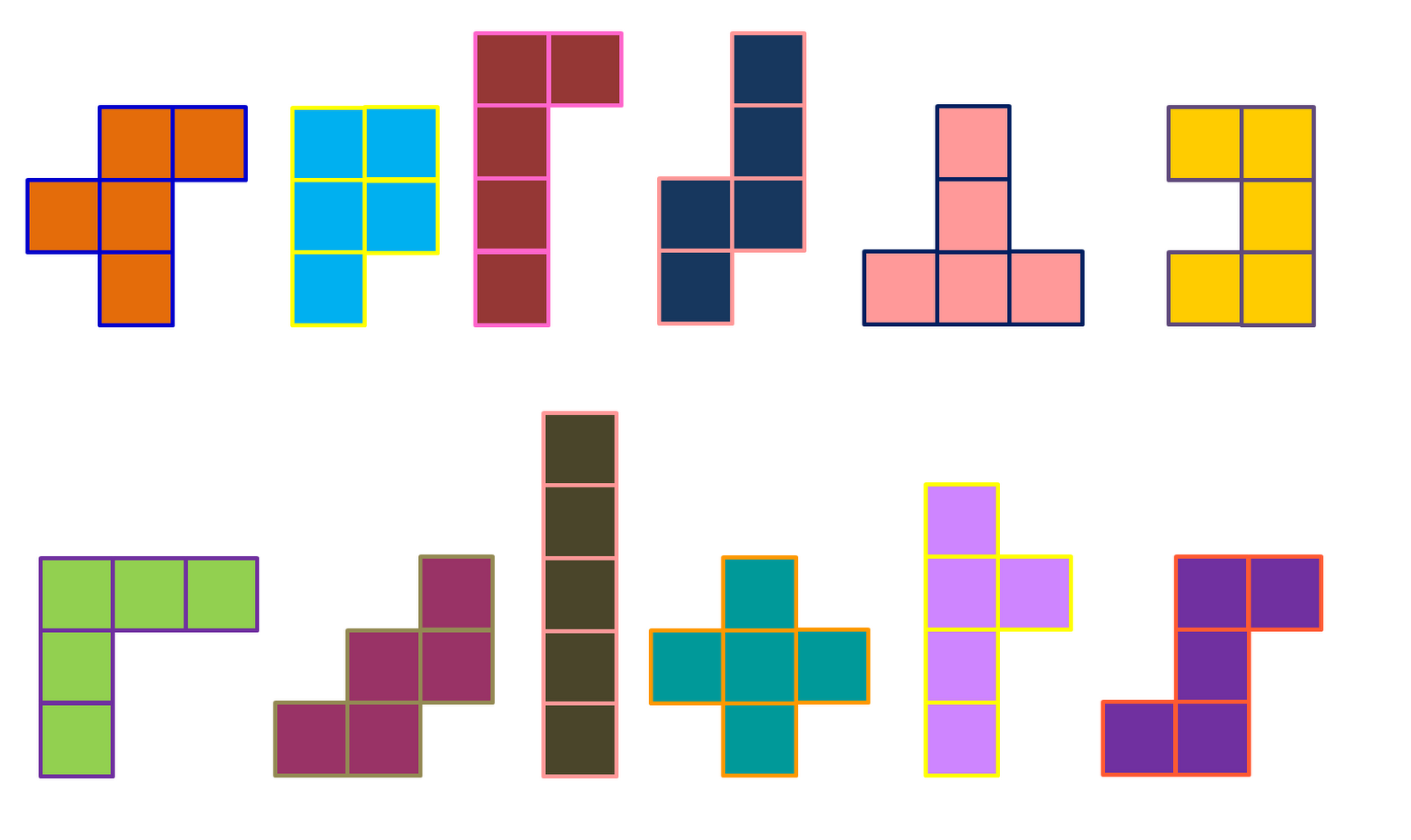
A pentomino is a shape formed by joining five equal squares along their edges. There are 12 different pentominoes.

http://donsteward.blogspot.com/2012/04/pentominoes.html

https://commons.wikimedia.org/wiki/File:Pentomino_sol.svg

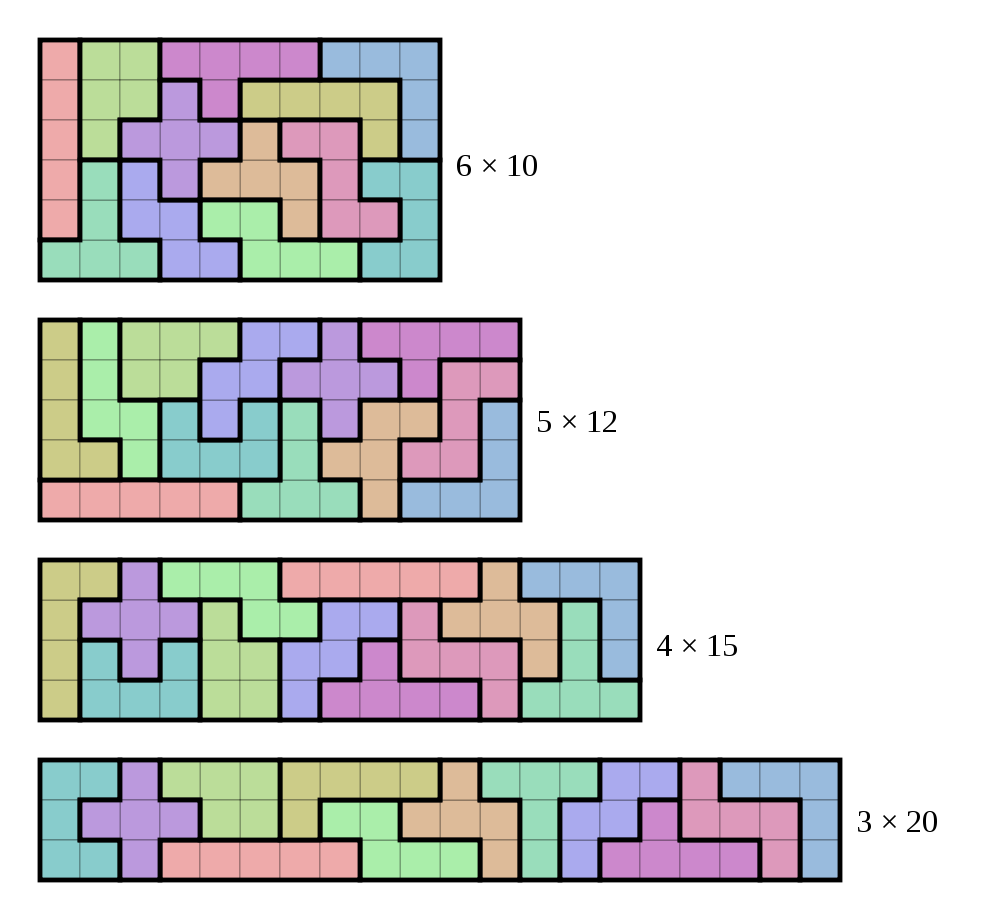
Pentomino Puzzles

How many ways are there to tile an 8x8 square with all 12 pentominoes, if the corners are removed?

(Answer: 2170)

Tiling a clipped square

The Exact Cover Problem

Input:      A matrix of zeros and ones.

Output:  A set of rows such that every column adds to 1.

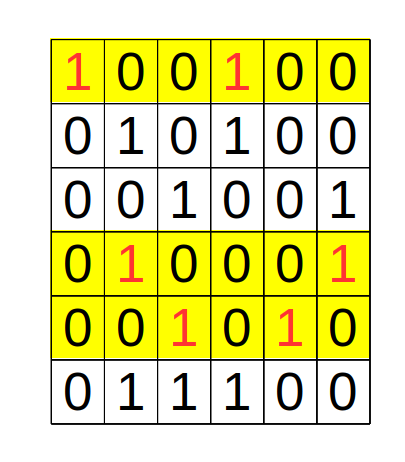
Algorithm X

1.   If the matrix A has no columns, terminate successfully.
2.  Choose a column c with minimal sum.
3.  For each row r having a 1 in column c,
4.          Include r in the partial solution,
5.          Delete all rows that intersect row r,
6.          Delete all columns have a 1 in row r,
7.          Repeat the algorithm recursively on the reduced matrix.

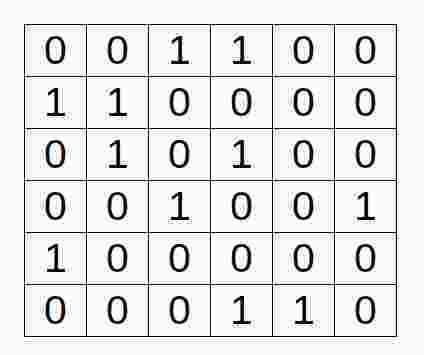
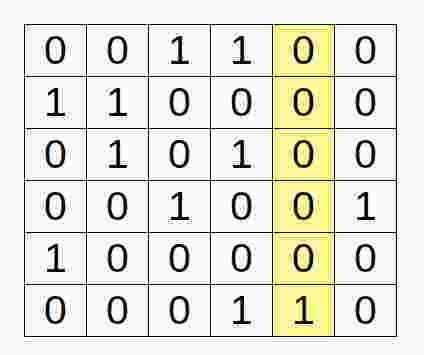
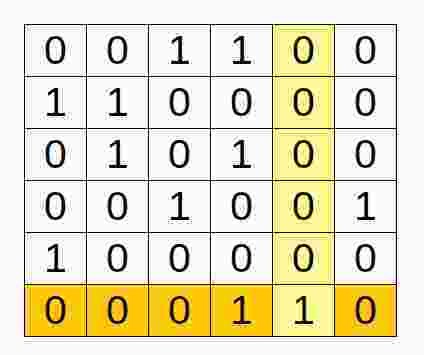
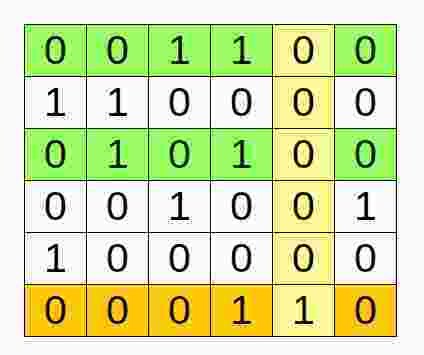
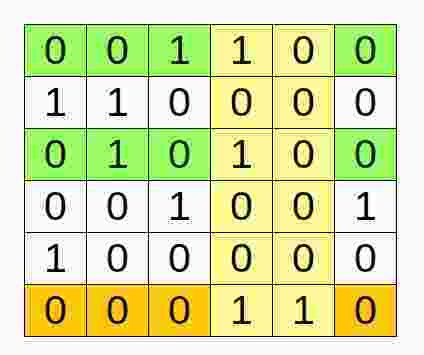
Algorithm X Example

def exact_cover(A):
    # If matrix has no columns, terminate successfully.
    if A.shape[1] == 0:
        yield []                                    
    else:
        # Choose a column c with the fewest 1s.
        c = A.sum(axis=0).argmin()

        # For each row r such that A[r,c] = 1,                  
        for r in A.index[A[c] == 1]:                
            B = A

            # For each column j such that A[r,j] = 1,
            for j in A.columns[A.loc[r] == 1]:

                # Delete each row i such that A[i,j] = 1      
                B = B[B[j] == 0]

                # then delete column j.                  
                del B[j]              
              
            for partial_solution in exact_cover(B):
                # Include r in the partial solution.
                yield [r] + partial_solution        

Python implementation of Algorithm X

Implementing a Pentomino Solver

The Matrix

The first 49 rows of the input matrix.

import pandas as pd
import numpy as np
from knuth import exact_cover

pentominoes = [
    np.array(p) for p in [

        # F
        [[0,1,1],  
         [1,1,0],
         [0,1,0]],
        
        # I
        [[1,1,1,1,1]],
        
        # L
        [[1,1,1,1],
         [0,0,0,1]],
        
        # N
        [[1,1,0,0],
         [0,1,1,1]],
        
        # P
        [[1,1,1],
         [0,1,1]],
        
        # T
        [[1,1,1],
         [0,1,0],
         [0,1,0]],
        
        # U
        [[1,0,1],
         [1,1,1]],
        
        # V
        [[1,0,0],
         [1,0,0],
         [1,1,1]],
        
        # W
        [[1,0,0],
         [1,1,0],
         [0,1,1]],
        
        # X
        [[0,1,0],
         [1,1,1],
         [0,1,0]],
        
        # Y
        [[0,0,1,0],
         [1,1,1,1]],
        
        # Z
        [[1,1,0],
         [0,1,0],
         [0,1,1]]
    ]
]

def all_orientations(A, i):
    """Generate all distinct orientations of the pentominoes,
    including rotations and reflections."""

    # Fixing the orientation of the first (F) pentomino eliminates
    # redundant solutions resulting from rotations or reflections."""
    if i == 0:
        yield A
        return
        
    seen = set()
    # Apply transpose, left/right flip, and up/down flip in all combinations
    # to generate all possible orientiations of a pentomino.
    for A in (A, A.T):
        for A in (A, np.fliplr(A)):
            for A in (A, np.flipud(A)):
                s = str(A)
                if not s in seen:
                    yield A
                    seen.add(s)


def all_positions(A, i):
    """ Find all positions to place the pentominoes. """
    for A in all_orientations(A, i):
        rows, cols = A.shape
        for i in range(9 - rows):
            for j in range(9 - cols):
                M = np.zeros((8, 8), dtype='int')
                M[i:i+rows, j:j+cols] = A
                if M[0,0] == M[0,7] == M[7,0] == M[7,7] == 0:
                    yield np.delete(M.reshape(64), [0, 7, 56, 63])

rows = []
for i, P in enumerate(pentominoes):
    for A in all_positions(P, i):
        A = np.append(A, np.zeros(12, dtype='int'))
        A[60+i] = 1
        rows.append(list(A))

A = pd.DataFrame(rows)
A.to_csv('matrix.csv')
covers = np.array(list(exact_cover(A)), dtype='int')
np.savetxt('exact-covers.csv', covers, delimiter=',', fmt='%d')

Pentomino solver in Python.

Sudoku as an exact cover problem

• 729 rows (ways to write one number in the grid).
• Delete any rows that are contradicted by the hints.
• 324 columns enforce the following conditions:

1. Every square is filled,
2. Every number occurs in every row,
3. Every number occurs in every column,
4. Every number occurs in every 3x3 block.

Note that each row has 4 ones and 320 zeros.

import numpy as np
import pandas as pd
from knuth import exact_cover

p = [int(x) for x in (
    "010009000"
    "743002000"
    "000800102"
    "000000400"
    "000060050"
    "009001007"
    "005000060"
    "001000900"
    "000750801"
)]

p = np.array(p).reshape((9,9))
A = np.zeros((729, 324), dtype=int)

row = 0
index = []
for i in range(9):
    for j in range(9):
        rng = [p[i,j]-1] if p[i,j] else range(9)
        for k in rng:
            A[row, 9*i + k] = 1
            A[row, 81 + 9*j + k] = 1
            A[row, 162 + 27*(i//3) + 9*(j//3) + k] = 1
            A[row, 243 + 9*i + j] = 1
            index.append("%d %d %d" % (i,j,k))
            row += 1
A = pd.DataFrame(A[:row,:], index=index)

solution = next(exact_cover(A))
m = np.zeros((9,9), dtype=int)
for s in solution:
    i, j, k = map(int, s.split())
    m[i, j] = k + 1
print (m)

Sudoku solver in Python