Measuring Sorts

• Number of comparisons
• Number of swaps

Big O of sorts boils down to two main factors:

Measuring Sorts

In order to know that two elements are out of order, we have to compare them

Number of comparisons:

[1, 7, 5]

Comparing reveals that these are not ordered!

Measuring Sorts

Once we've found out of order elements, we have to re-order the elements.

Number of swaps:

[1, 7, 5]

[1, 5, 7]

Bubble Sort

Bubble Sort is an algorithm which always examines adjacent elements, swapping those  which are "out of order"

Bubble Sort

We start at index 0 and compare the item to the right:

[5, 6, 3, 2, 1]

This time, the two elements are already ordered properly

Bubble Sort

So we slide the window one to the right

[5, 6, 3, 2, 1]

Comparing reveals we have to swap!

Bubble Sort

[5, 3, 6, 2, 1]

We swapped the 3 and 6. Then, we continue to slide the comparison window to the right.

Bubble Sort

Following this process will *always* result in the highest element being "bubbled" to the top.

[5, 3, 6, 2, 1]

[5, 3, 2, 6, 1]

[5, 3, 2, 1, 6]

Now - the top element is in it's place. We just repeat the process for the items to the left of 6.

Bubble Sort

Bubble Sort is an algorithm which always examines adjacent elements, swapping those  which are "out of order"

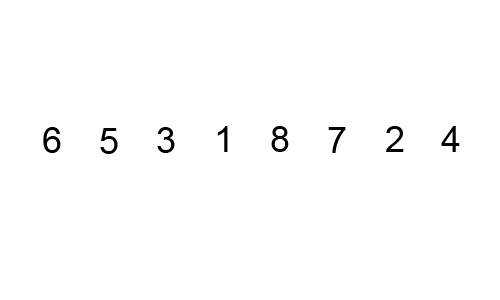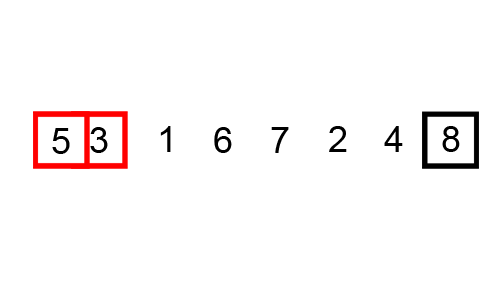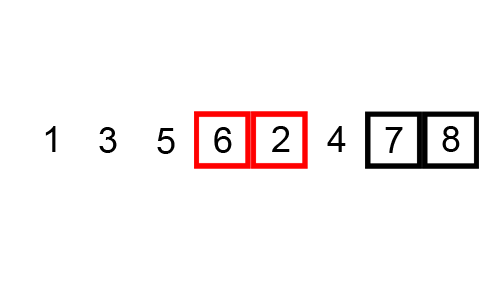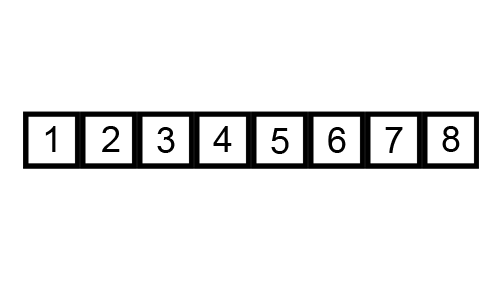
What is the worst case scenario for this algorithm?

How many comparisons per iteration? How many swaps?

How many maximum iterations?

Bubble Sort

Big O

Bubble Sort

Big O

What is the worst case scenario for this algorithm?

When the list is in reverse order.

How many comparisons per iteration? How many swaps?

The first iteration has n. Second has n-1. Third has n-2 ... and so on. Swaps are the same, but you may to fewer swaps in better cases.

How many maximum iterations?

n

Bubble Sort

Big O

So Bubble Sort is

O(n^2)

Selection Sort

Selection sort is an algorithm which "selects" the minimum value in a list, then puts that minimum value where it belongs.

Selection Sort

Each iteration examines every element in the list and finds the min.

[5, 6, 3, 2, 1]

min = ?

Comparing from left to right the comparisons would be:

5 to 6, 5 to 3, 3 to 2, 2 to 1

1 ends up being the min

Selection Sort

When we find the min, we swap it to the place it belongs.

[5, 6, 3, 2, 1]

[1, 6, 3, 2, 5]

min = 1, at index 4

Selection Sort

Now, we repeat the process for all items to the right of 1.

[1, 6, 3, 2, 5]

Selection Sort

Big O

What is the worst case scenario for this algorithm?

It doesn't matter.

How many comparisons per iteration? How many swaps?

Comparisons are always n per iteration.

Swaps are always 1 per iteration

How many maximum iterations?

Always n iterations.

Selection Sort

Big O

What is the worst case scenario for this algorithm?

How many comparisons per iteration? How many swaps?

How many maximum iterations?

Selection Sort

Big O

So Selection sort is

O(n^2)

Insertion Sort

Insertion sort divides the list into two portions: sorted and unsorted.

At each step, insertion sort takes the first "unsorted" value, and puts it in the correct location in the "sorted" section.

Insertion Sort

Step 1, call the first element "sorted"

[5, 4, 3, 2, 1]

Sorted & Unsorted

Insertion Sort

For all the following iterations, select the first item off of the "unsorted" section, and slide it down the sorted section until it fits.

[5, 4, 3, 2, 1]

=> (compare 5 to 4)

[4, 5, 3, 2, 1]

=> (compare 3 to 5, then to 4)

[3, 4, 5, 2, 1]

Insertion Sort

For all the following iterations, select the first item off of the "unsorted" section, and slide it down the sorted section until it fits.

[5, 4, 3, 2, 1]

=> (compare 5 to 4)

[4, 5, 3, 2, 1]

=> (compare 3 to 5, then to 4)

[3, 4, 5, 2, 1]

Insertion Sort

What is the worst case scenario for this algorithm?

How many comparisons per iteration? How many swaps?

How many maximum iterations?

Insertion Sort

What is the worst case scenario for this algorithm?

If the list is in reverse order.

How many comparisons per iteration? How many swaps?

Up to n comparisons per iteration.

1 swap per iteration.

How many maximum iterations?

n

Insertion Sort

So insertion sort is big O(n^2) in the worst case.

Unlike the last two algorithms, insertion sort might do significantly fewer comparisons depending on the input order...

Whats the best case for insertion sort?

Insertion Sort

but what is the complexity for the best case?

The best case is when the list is already sorted. If we have a sorted list, then insertion sort will finish in linear time!

Insertion sort is great on "nearly sorted" data.

Quick Sort

Quick Sort

Step 1 - pick a pivot.

The most basic version of quick sort picks one at random. There are other strategies that can result in better "average case" performance

[15, 7, 1, 4, 6, 3, 0, 9, 12]

Quick Sort

Step 2 - reorder the list so that elements less than our pivot (9) are to the left of it.

[15, 7, 1, 4, 6, 3, 0, 9, 12]

=>

[7, 1, 4, 6, 3, 0, 9, 15, 12]

Now, we have two unsorted sub-lists and single sorted list of size 1.

[7, 1, 4, 6, 3, 0], [9], [15, 12]

Quick Sort

Recursion -- repeat this process on our new lists.

[7, 1, 4, 6, 3, 0], [9], [15, 12]

=>

[1, 3, 0], [4], [7, 6], [9], [12], [15]

=>

[0], [1], [3], [4], [6], [7], [9], [12], [15]

Notice that all the lists of size 1 are sorted.

Quick Sort

Pseudocode:

Text

function quickSort(arr) {
    if (arr.length < 2)
    	return arr
    else 
    	leftArr = []
    	rightArr = []
    	pivot = arr[arr.length - 1]
    	for element in arr
    		if element > pivot
    			rightArr.push(element)
    		else 
    			leftArr.push(element)
    	
    	return quicksort(leftArr) + pivot + quicksort(rightArr)
}

Quick Sort

Big O

What is the worst case scenario for this algorithm?

How many recursive branches per step?

How much work at each recursive branch?

Quick Sort

Big O

What is the worst case scenario for this algorithm?

When we always select the highest or lowest value as the pivot.

How many recursive branches per step?

1

How much work at each recursive branch?

n

So ... O(n^2)

Quick Sort

Big O

What is the best case scenario for this algorithm?

How many recursive branches per step?

How much work at each recursive branch?

Quick Sort

Big O

What is the best case scenario for this algorithm?

When we always select the exact middle as pivot

How many recursive branches per step?

2

How much work at each recursive branch?

n / 2

So ... O(n log n)

Quick Sort

Big O

On average, QuickSort is also n log n.

intuitively this is because always randomly picking the highest or lowest item is exceedingly unlikely.

Some implementations of Quick Sort try to cleverly choose a pivot to reduce the odds of the worst case scenario.

Quick Sort

Wrinkles:

It turns out there are many ways to do this. Here is one way using our first pivot as the example:

[15, 7, 1, 4, 6, 3, 0, 9, 12]

Quick Sort

Pivot Shuffle Step 1: Swap the pivot into the right most index.

[15, 7, 1, 4, 6, 3, 0, 9, 12]

=>

[15, 7, 1, 4, 6, 3, 0, 12, 9]

Quick Sort

Pivot Shuffle Step 2: Keep an index pivotCount which gets updated every time we find a value less than the pivot:

pivotCount = 0

i = 0

[15, 7, 1, 4, 6, 3, 0, 12, 9] // too big

Quick Sort

Pivot Shuffle Step 2: When we find an item less than the pivot, swap the items at i and pivotCount

pivotCount = 0

i = 1

[15, 7, 1, 4, 6, 3, 0, 12, 9] // smaller

Swap 0 and 1

[7,  15, 1, 4, 6, 3, 0, 12, 9] // 7 is now locked

pivotCount++

Quick Sort

Pivot Shuffle Step 2: Repeat this for each element

pivotCount = 1

i = 2

[7,  15, 1, 4, 6, 3, 0, 12, 9] // smaller

1 < 9, so swap items 1 & 2

[7,  1, 15, 4, 6, 3, 0, 12, 9] // 7 & 1 locked

Quick Sort

Pivot Shuffle Step 2: Repeat this for each element

[7,  1, 15, 4, 6, 3, 0, 12, 9] => pivotCount = 2

[7,  1, 4, 15, 6, 3, 0, 12, 9] => pivotCount = 3

[7,  1, 4, 6, 15, 3, 0, 12, 9] => pivotCount = 4

[7,  1, 4, 6, 3, 15, 0, 12, 9] => pivotCount = 5

[7,  1, 4, 6, 3, 0, 15, 12, 9] => pivotCount = 6

15 and 12 do not swap since both are larger than 9

Quick Sort

Pivot Shuffle final step: put the pivot at pivotCount

[7,  1, 4, 6, 3, 0, 15, 12, 9] => pivotCount = 6

we put the pivot where it belongs by swapping

[7,  1, 4, 6, 3, 0, 9, 12, 15 ]

Merge Sort

Merge Sort is an algorithm that starts by "creating" n lists of size 1. Each size 1 list is, by definition sorted.

[15, 7, 1, 4, 6, 3, 0, 9]

=>

[15], [7], [1], [4], [6], [3], [0], [9]

Merge Sort

Once we have these n sorted lists we "merge" them. First we merge our lists of size 1 into lists of size 2. This merge process ensures the lists remain sorted:

[15], [7], [1], [4], [6], [3], [0], [9]

7 < 15, so swap the order when making size 2 list:

[7, 15], [1], [4], [6], [3], [0], [9]

Merge Sort

Repeat this merge until we have only lists of size 2:

[7, 15], [1], [4], [6], [3], [0], [9] =>

[7, 15], [1, 4], [3, 6], [0, 9]

Merge Sort

Now, merge these lists until we have lists of size 4. The process for these merges is:

1. Pick two lists

2. Compare their lowest elements

3. whichever is lowest goes in the new lists lowest slot

[7, 15], [1, 4], [3, 6], [0, 9]

Merge Sort

Now, merge these lists until we have lists of size 4. The process for these merges is:

1. Pick two lists

2. Compare their lowest elements

3. whichever is lowest goes in the new lists lowest slot

[7, 15], [1, 4], [3, 6], [0, 9]

Merge Sort

Now, merge these lists until we have lists of size 4. The process for these merges is:

1. Pick two lists

2. Compare their lowest elements

3. whichever is lowest goes in the new lists lowest slot

[7, 15], [1, 4], [3, 6], [0, 9]

Merge Sort

Now, merge these lists until we have lists of size 4. The process for these merges is:

1. Pick two lists

2. Compare their lowest elements

3. whichever is lowest goes in the new lists lowest slot

[7, 15], [4], [3, 6], [0, 9]

=>

[1]

Merge Sort

Now, merge these lists until we have lists of size 4. The process for these merges is:

Repeat

[7, 15], [4], [3, 6], [0, 9]

=>

[1, 4]

Merge Sort

Now, merge these lists until we have lists of size 4. The process for these merges is:

The lower list is *already sorted* so now that we're out of elements in the second list, add [7, 15] to the merged list

[7, 15], [], [3, 6], [0, 9]

=>

[1, 4, 7, 15]

=>

[1, 4, 7, 15], [3, 6], [0, 9]

Merge Sort

Now, merge these lists until we have lists of size 4. The process for these merges is:

Continue the process on our other lists size 2 and 1

[1, 4, 7, 15], [3, 6], [0, 9]

[0]

[3, 6], [9]

[0, 3]

[6], [9]

[0, 3, 6, 9]

Merge Sort

Finally, merge the size 4 lists to a size 8:

[1, 4, 7, 15], [0, 3, 6, 9] => [0]

[1, 4, 7, 15], [3, 6, 9] => [0, 1]

[4, 7, 15], [3, 6, 9] => [0, 1, 3]

[4, 7, 15], [6, 9] => [0, 1, 3, 4]

[7, 15], [6, 9] => [0, 1, 3, 4, 6]

[7, 15], [9] => [0, 1, 3, 4, 6, 7]

[15], [9] => [0, 1, 3, 4, 6, 7, 9]

[15], [] => [0, 1, 3, 4, 6, 7, 9, 15]

[0, 1, 3, 4, 6, 7, 9, 15]

Merge Sort

What is the worst case scenario for this algorithm?

How many recursive branches per step?

How much work at each recursive branch?

Merge Sort

What is the worst case scenario for this algorithm?

It doesn't matter!

How many recursive branches created in total?

Log n (list sizes double each time)

How much work at each recursive branch?

n - we may compare every element to every element at each list size

Merge Sort

so

log n recursive branches.

n work on each branch.

O(n log n)