Deep Learning

- Crash Course -

UNIFEI - August, 2018

Hello!

Prof. Luiz Eduardo

Hanneli Tavante

<3

Canada

Prof. Maurilio

<3

Deutschland

Questions

  • What is this course? 
    • A: An attempt to bring interesting subjects to the courses
  • Why are the slides in English?
    • I am reusing some material that I prepared before
  • What should I expect?
    • This is the first time we give this course. We will be looking forward to hearing your feedback

Rules

  • Don't skip classes
  • The final assignment is optional
  • We will have AN OPTIONAL LECTURE on Friday
  • Feel free to ask questions
  • Don't feel discouraged with the mathematics
  • Contact us for study group options

[GIF time]

Agenda

  1. Why is deep learning so popular now?
  2. Introduction to Machine Learning
  3. Introduction to Neural Networks
  4. Deep Neural Networks
  5. Training and measuring the performance of the N.N.
  6. Regularization
  7. Creating Deep Learning Projects
  8. CNNs and RNNs
  9. (OPTIONAL): Tensorflow intro

Note: this list can change

Topics

  1. Why is deep learning so popular now?
  2. Introduction to Machine Learning
  3. Introduction to Neural Networks
  4. Deep Neural Networks
  5. Training and measuring the performance of the N.N.
  6. Regularization
  7. Creating Deep Learning Projects
  8. CNNs and RNNs
  9. (OPTIONAL): Tensorflow intro

Note: this list can change

What is the difference between Machine Learning (ML) and Deep Learning (DL)? And AI?

AI

ML

Representation Learning

DL

Why is it so popular?

  • Big companies are using it
  • Business opportunities
  • It is easy to understand the main idea
  • More accessible outside the Academia
  • Lots os commercial applications
  • Large amount of data
  • GPUs and fast computers

Agenda

  1. Why is deep learning so popular now?
  2. Introduction to Machine Learning
  3. Introduction to Neural Networks
  4. Deep Neural Networks
  5. Training and measuring the performance of the N.N.
  6. Regularization
  7. Creating Deep Learning Projects
  8. CNNs and RNNs
  9. (OPTIONAL): Tensorflow intro

~switching presentations~

WHERE ARE THE

NEURAL

NETWORKS??////??

<3

Canada

Agenda

  1. Why is deep learning so popular now?
  2. Introduction to Machine Learning (we are still here)
  3. Introduction to Neural Networks
  4. Deep Neural Networks
  5. Training and measuring the performance of the N.N.
  6. Regularization
  7. Creating Deep Learning Projects
  8. CNNs and RNNs
  9. (OPTIONAL): Tensorflow intro

Example: predict if a given image is the picture of a dog

Our Data and Notation

(x, y) ; x \in \mathbb{R}^n; y \in {0, 1}
(x,y);x∈Rn;y∈0,1(x, y) ; x \in \mathbb{R}^n; y \in {0, 1}

Let us use the Logistic Regression example

Single training example

We will have multiple training examples:

m training examples in a set

{ (x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), ..., (x^{(m)}, y^{(m)})}
(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m)){ (x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), ..., (x^{(m)}, y^{(m)})}

Warning:

( [

x^{(1)}_1
x1(1)x^{(1)}_1

],

x^{(1)}_2
x2(1)x^{(1)}_2
First x vector First y (number)
Second x vector Second y (number)
... ...
x^{(1)}_3
x3(1)x^{(1)}_3
x^{(1)}_4
x4(1)x^{(1)}_4
y^{(1)}
y(1)y^{(1)}

)

Warning:

( [

x^{(1)}_1
x1(1)x^{(1)}_1

],

x^{(1)}_2
x2(1)x^{(1)}_2
First x vector First y (number)
Second x vector Second y (number)
... ...
x^{(1)}_3
x3(1)x^{(1)}_3
x^{(1)}_4
x4(1)x^{(1)}_4
y^{(1)}
y(1)y^{(1)}

)

( [

x^{(2)}_1
x1(2)x^{(2)}_1

],

x^{(2)}_2
x2(2)x^{(2)}_2
x^{(2)}_3
x3(2)x^{(2)}_3
x^{(2)}_4
x4(2)x^{(2)}_4
y^{(2)}
y(2)y^{(2)}

)

Pro tip:

[

x^{(1)}_1
x1(1)x^{(1)}_1
x^{(1)}_2
x2(1)x^{(1)}_2
First x vector First y (number)
Second x vector Second y (number)
... ...
x^{(1)}_3
x3(1)x^{(1)}_3
x^{(1)}_4
x4(1)x^{(1)}_4
x^{(2)}_1
x1(2)x^{(2)}_1

...]

x^{(2)}_2
x2(2)x^{(2)}_2
x^{(2)}_3
x3(2)x^{(2)}_3
x^{(2)}_4
x4(2)x^{(2)}_4

m

n

Pro tip:

[

x^{(1)}_1
x1(1)x^{(1)}_1
x^{(1)}_2
x2(1)x^{(1)}_2
First x vector First y (number)
Second x vector Second y (number)
... ...
x^{(1)}_3
x3(1)x^{(1)}_3
x^{(1)}_4
x4(1)x^{(1)}_4
x^{(2)}_1
x1(2)x^{(2)}_1

...]

x^{(2)}_2
x2(2)x^{(2)}_2
x^{(2)}_3
x3(2)x^{(2)}_3
x^{(2)}_4
x4(2)x^{(2)}_4

m

n

[

y^{(1)}
y(1)y^{(1)}
y^{(2)}
y(2)y^{(2)}

...]

Data:

[salary, location, tech...] Probability y=1
[RGB values] 0.8353213
... ...

In logistic regression, we want to know the probability of y=1 given a vector of x

\hat{y} = P(y=1 | x)
y^=P(y=1∣x)\hat{y} = P(y=1 | x)

(note: we could have more columns for extra features)

Logistic regression

Recap: for logistic regression, what is the equation format?

Tip: Sigmoid, transpose, wx+b

w_1
w1w_1
w_2
w2w_2
w_3
w3w_3
x_1
x1x_1
x_2
x2x_2
x_3
x3x_3

*

Logistic regression

Recap: for logistic regression, what is the equation format?

Tip: Sigmoid, transpose, wx+b

w_1
w1w_1
w_2
w2w_2
w_3
w3w_3
x_1
x1x_1
x_2
x2x_2
x_3
x3x_3

*

+

b

z

Logistic regression

Recap: for logistic regression, what is the equation format?

Tip: Sigmoid, transpose, wx+b

w_1
w1w_1
w_2
w2w_2
w_3
w3w_3
x_1
x1x_1
x_2
x2x_2
x_3
x3x_3

*

+

b

z

\hat{y} = \sigma
y^=σ\hat{y} = \sigma

(

)

\sigma=\frac{1}{1+e^{-z}}
σ=11+e−z\sigma=\frac{1}{1+e^{-z}}

Logistic regression

Recap: given a training set

{ (x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), ..., (x^{(m)}, y^{(m)})}
(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m)){ (x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), ..., (x^{(m)}, y^{(m)})}

You want

\hat{y}^{i} \approx y^i
y^i≈yi\hat{y}^{i} \approx y^i

What do we do now?

loss = -y \log(h(x)) - (1-y)\log(1 - h(x))
loss=−ylog⁡(h(x))−(1−y)log⁡(1−h(x))loss = -y \log(h(x)) - (1-y)\log(1 - h(x))

For each training example

Logistic regression

L(\hat{y}, y) = -y \log(\hat{y}) - (1-y)\log(1 - \hat{y})
L(y^,y)=−ylog⁡(y^)−(1−y)log⁡(1−y^)L(\hat{y}, y) = -y \log(\hat{y}) - (1-y)\log(1 - \hat{y})

For each training example

If y = 1, you want

\hat{y}
y^\hat{y}

large

If y = 0, you want

\hat{y}
y^\hat{y}

small

What do we do now?

Cost function: applies the loss function to the entire training set

J(w, b) = \frac{1}{m} \sum_{i=1}^{m} [L(\hat{y}, y) ]
J(w,b)=1m∑i=1m[L(y^,y)]J(w, b) = \frac{1}{m} \sum_{i=1}^{m} [L(\hat{y}, y) ]

Logistic regression

What do we do now?

Cost function: measures how well your parameters are doing in the training set

J(w, b) = \frac{1}{m} \sum_{i=1}^{m} [L(\hat{y}, y) ]
J(w,b)=1m∑i=1m[L(y^,y)]J(w, b) = \frac{1}{m} \sum_{i=1}^{m} [L(\hat{y}, y) ]

We want to find w and b that minimise J(w, b)

Gradient Descent: it points downhill

It's time for the partial derivatives

Logistic regression

J(w, b) = \frac{1}{m} \sum_{i=1}^{m} [L(\hat{y}, y) ]
J(w,b)=1m∑i=1m[L(y^,y)]J(w, b) = \frac{1}{m} \sum_{i=1}^{m} [L(\hat{y}, y) ]

Gradient Descent: It's time for the partial derivatives

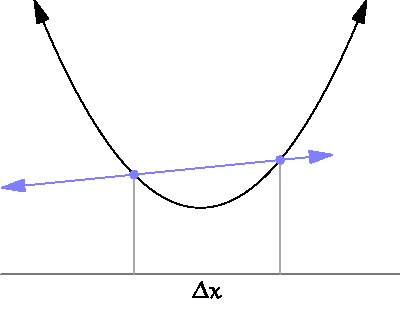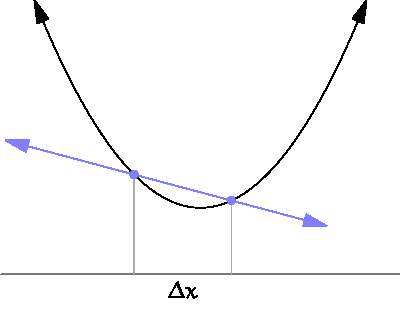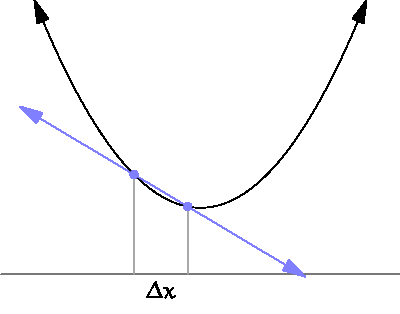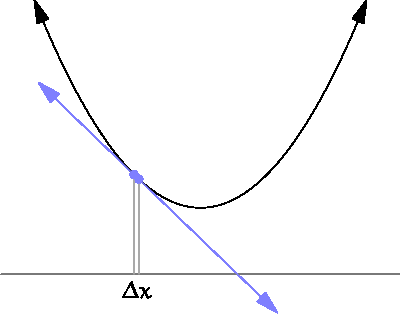
source: https://www.wikihow.com/Take-Derivatives

Logistic regression

J(w, b) = \frac{1}{m} \sum_{i=1}^{m} [L(\hat{y}, y) ]
J(w,b)=1m∑i=1m[L(y^,y)]J(w, b) = \frac{1}{m} \sum_{i=1}^{m} [L(\hat{y}, y) ]

We are looking at the previous step to calculate the derivative

source: https://www.wikihow.com/Take-Derivatives

Whiteboard time - computation graphs and derivatives

Let's put these concepts together

x

w

b

z=w^T+b
z=wT+bz=w^T+b
\hat{y} = a = \sigma(z)
y^=a=σ(z)\hat{y} = a = \sigma(z)
L(\hat{y}, y) = L(a, y)
L(y^,y)=L(a,y)L(\hat{y}, y) = L(a, y)

Forward pass

What is our goal?

Adjust the values of w and b in order to MINIMIZE difference at the loss function

x

w

b

z=w^T+b
z=wT+bz=w^T+b
\hat{y} = a = \sigma(z)
y^=a=σ(z)\hat{y} = a = \sigma(z)
L(\hat{y}, y) = L(a, y)
L(y^,y)=L(a,y)L(\hat{y}, y) = L(a, y)

How do we compute the derivative?

The equations: (whiteboard)

Backwards step

x

w

b

z=w^T+b
z=wT+bz=w^T+b
\hat{y} = a = \sigma(z)
y^=a=σ(z)\hat{y} = a = \sigma(z)
L(\hat{y}, y) = L(a, y)
L(y^,y)=L(a,y)L(\hat{y}, y) = L(a, y)

Good news: this looks like a Neural Network!

Agenda

  1. Why is deep learning so popular now?
  2. Introduction to Machine Learning
  3. Introduction to Neural Networks
  4. Deep Neural Networks
  5. Training and measuring the performance of the N.N.
  6. Regularization
  7. Creating Deep Learning Projects
  8. CNNs and RNNs
  9. (OPTIONAL): Tensorflow intro

Basic structure of a Neural Network

x_1
x1x_1
x_2
x2x_2
x_3
x3x_3

Hidden

Layer

\hat{y}
y^\hat{y}

More details

x_1
x1x_1
x_2
x2x_2
x_3
x3x_3

Hidden Layer

\hat{y}
y^\hat{y}

Hidden Layer

In each hidden unit of each layer, a computation happens. For example:

z=w^T+b
z=wT+bz=w^T+b
a = \sigma(z)
a=σ(z)a = \sigma(z)

Naming convention

x_1
x1x_1
x_2
x2x_2
x_3
x3x_3

Hidden Layer

\hat{y}
y^\hat{y}

Hidden Layer

a^{[1]}
a[1]a^{[1]}
a^{[1]}_1
a1[1]a^{[1]}_1
a^{[1]}_3
a3[1]a^{[1]}_3
a^{[1]}_2
a2[1]a^{[1]}_2
a^{[2]}
a[2]a^{[2]}
a^{[2]}_1
a1[2]a^{[2]}_1
a^{[1]} = [a^{[1]}_1, a^{[1]}_2, a^{[1]}_3]
a[1]=[a1[1],a2[1],a3[1]]a^{[1]} = [a^{[1]}_1, a^{[1]}_2, a^{[1]}_3]
a^{[2]} = \hat{y}
a[2]=y^a^{[2]} = \hat{y}
X = a^{[0 ]}
X=a[0]X = a^{[0 ]}

Key question: Every time we see a, what do we need to compute?

a = \sigma(z)
a=σ(z)a = \sigma(z)

To make it clear

x_1
x1x_1
x_2
x2x_2
x_3
x3x_3

Hidden Layer

\hat{y}
y^\hat{y}

Hidden Layer

z^{[1]}_1=w^{[1]T}_1+b^{[1]}_1
z1[1]=w1[1]T+b1[1]z^{[1]}_1=w^{[1]T}_1+b^{[1]}_1
a^{[1]}_1 = \sigma(z^{[1]}_1)
a1[1]=σ(z1[1])a^{[1]}_1 = \sigma(z^{[1]}_1)
z^{[1]}_2=w^{[1]T}_2+b^{[1]}_2
z2[1]=w2[1]T+b2[1]z^{[1]}_2=w^{[1]T}_2+b^{[1]}_2
a^{[1]}_2 = \sigma(z^{[1]}_2)
a2[1]=σ(z2[1])a^{[1]}_2 = \sigma(z^{[1]}_2)
z^{[1]}_3=w^{[1]T}_3+b^{[1]}_3
z3[1]=w3[1]T+b3[1]z^{[1]}_3=w^{[1]T}_3+b^{[1]}_3
a^{[1]}_3 = \sigma(z^{[1]}_3)
a3[1]=σ(z3[1])a^{[1]}_3 = \sigma(z^{[1]}_3)
z^{[2]}_1=w^{[2]T}_1+b^{[2]}_1
z1[2]=w1[2]T+b1[2]z^{[2]}_1=w^{[2]T}_1+b^{[2]}_1
a^{[2]}_1 = \sigma(z^{[2]}_1)
a1[2]=σ(z1[2])a^{[2]}_1 = \sigma(z^{[2]}_1)

Questions

a = \sigma(z)
a=σ(z)a = \sigma(z)

1. What was the formula for the sigmoid function?

\sigma=\frac{1}{1+e^{-z}}
σ=11+e−z\sigma=\frac{1}{1+e^{-z}}

2. Why do we need the sigmoid function? How does it look like?

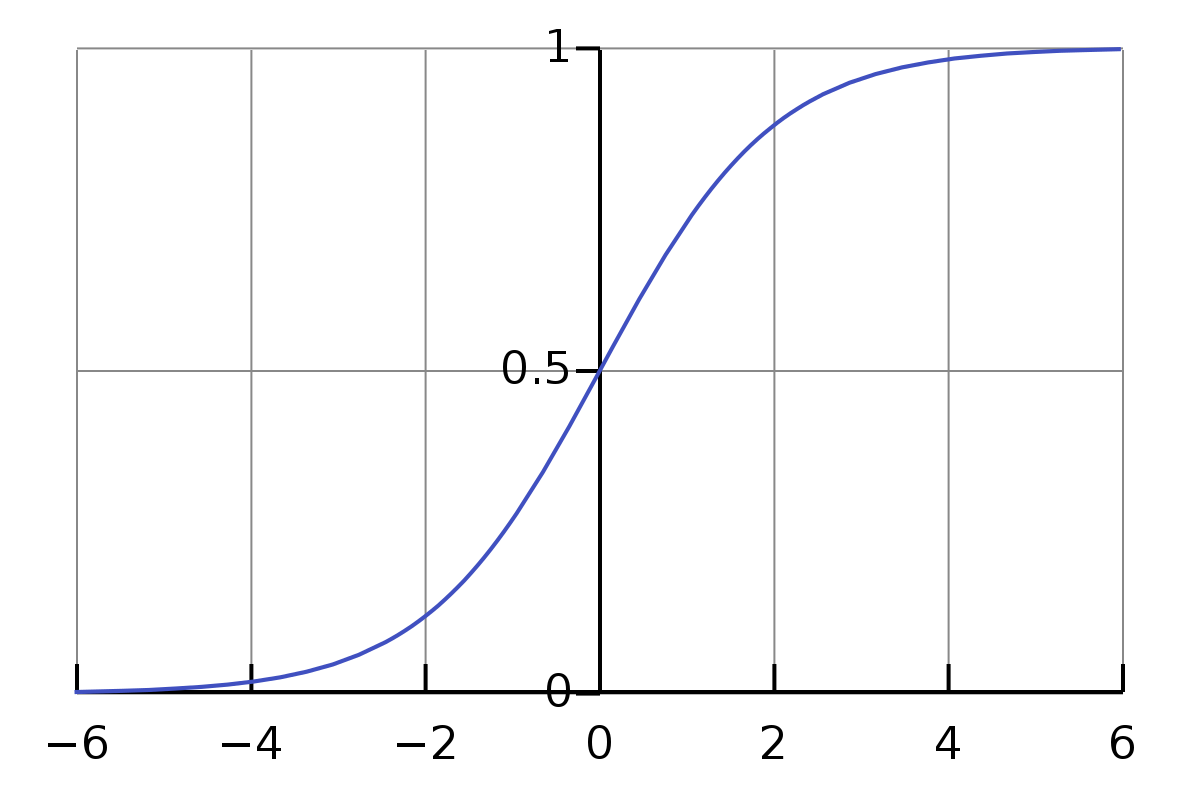
Questions

3. Can we use any other type of function?

The sigmoid function is what we call Activation Function 

Activation Functions

a = \sigma(z)=\frac{1}{1+e^{-z}}
a=σ(z)=11+e−za = \sigma(z)=\frac{1}{1+e^{-z}}
a = tanh(z)
a=tanh(z)a = tanh(z)

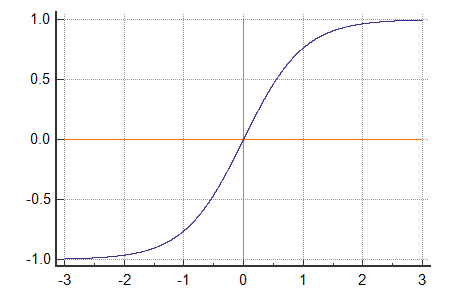
Activation Functions

a = max(0, z)
a=max(0,z)a = max(0, z)

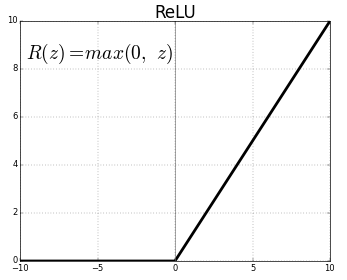
Rectified Linear Unit

(ReLU)

Note: The activation function can vary across the layers

Each of these activation functions has a derivative

[Question: Why do we need to know the derivatives? :) ]

g'(z) = \frac{d}{dz}g(z) = a(1-a)
g′(z)=ddzg(z)=a(1−a)g&#x27;(z) = \frac{d}{dz}g(z) = a(1-a)
a = g(z)
a=g(z)a = g(z)

Note

\sigma | tanh | ReLU = g
σ∣tanh∣ReLU=g\sigma | tanh | ReLU = g
g = \sigma
g=σg = \sigma

GIF Time! Too many things going on

Which parameters do we have until now?

Our Parameters

x_1
x1x_1
x_2
x2x_2
x_3
x3x_3
\hat{y}
y^\hat{y}
z^{[1]}_1=w^{[1]T}+b^{[1]}_1
z1[1]=w[1]T+b1[1]z^{[1]}_1=w^{[1]T}+b^{[1]}_1
a^{[1]}_1 = \sigma(z^{[1]}_1)
a1[1]=σ(z1[1])a^{[1]}_1 = \sigma(z^{[1]}_1)
z^{[1]}_2=w^{[1]T}+b^{[1]}_2
z2[1]=w[1]T+b2[1]z^{[1]}_2=w^{[1]T}+b^{[1]}_2
a^{[1]}_2 = \sigma(z^{[1]}_2)
a2[1]=σ(z2[1])a^{[1]}_2 = \sigma(z^{[1]}_2)
z^{[1]}_3=w^{[1]T}+b^{[1]}_3
z3[1]=w[1]T+b3[1]z^{[1]}_3=w^{[1]T}+b^{[1]}_3
a^{[1]}_3 = \sigma(z^{[1]}_3)
a3[1]=σ(z3[1])a^{[1]}_3 = \sigma(z^{[1]}_3)
z^{[2]}_1=w^{[2]T}+b^{[2]}_1
z1[2]=w[2]T+b1[2]z^{[2]}_1=w^{[2]T}+b^{[2]}_1
a^{[2]}_1 = \sigma(z^{[2]}_1)
a1[2]=σ(z1[2])a^{[2]}_1 = \sigma(z^{[2]}_1)
W^{[1]}
W[1]W^{[1]}
= [w^{[1]}_1, w^{[1]}_2, w^{[1]}_3]
=[w1[1],w2[1],w3[1]]= [w^{[1]}_1, w^{[1]}_2, w^{[1]}_3]

This is a matrix!

Our Parameters

x_1
x1x_1
x_2
x2x_2
x_3
x3x_3
\hat{y}
y^\hat{y}
z^{[1]}_1=w^{[1]T}+b^{[1]}_1
z1[1]=w[1]T+b1[1]z^{[1]}_1=w^{[1]T}+b^{[1]}_1
a^{[1]}_1 = \sigma(z^{[1]}_1)
a1[1]=σ(z1[1])a^{[1]}_1 = \sigma(z^{[1]}_1)
z^{[1]}_2=w^{[1]T}+b^{[1]}_2
z2[1]=w[1]T+b2[1]z^{[1]}_2=w^{[1]T}+b^{[1]}_2
a^{[1]}_2 = \sigma(z^{[1]}_2)
a2[1]=σ(z2[1])a^{[1]}_2 = \sigma(z^{[1]}_2)
z^{[1]}_3=w^{[1]T}+b^{[1]}_3
z3[1]=w[1]T+b3[1]z^{[1]}_3=w^{[1]T}+b^{[1]}_3
a^{[1]}_3 = \sigma(z^{[1]}_3)
a3[1]=σ(z3[1])a^{[1]}_3 = \sigma(z^{[1]}_3)
z^{[2]}_1=w^{[2]T}+b^{[2]}_1
z1[2]=w[2]T+b1[2]z^{[2]}_1=w^{[2]T}+b^{[2]}_1
a^{[2]}_1 = \sigma(z^{[2]}_1)
a1[2]=σ(z1[2])a^{[2]}_1 = \sigma(z^{[2]}_1)
W^{[1]}
W[1]W^{[1]}
b^{[1]}
b[1]b^{[1]}
= [b^{[1]}_1, b^{[1]}_2, b^{[1]}_3]
=[b1[1],b2[1],b3[1]]= [b^{[1]}_1, b^{[1]}_2, b^{[1]}_3]

Is b a vector or a matrix? 

A: It is a vector

Our Parameters

x_1
x1x_1
x_2
x2x_2
x_3
x3x_3
\hat{y}
y^\hat{y}
z^{[1]}_1=w^{[1]T}+b^{[1]}_1
z1[1]=w[1]T+b1[1]z^{[1]}_1=w^{[1]T}+b^{[1]}_1
a^{[1]}_1 = \sigma(z^{[1]}_1)
a1[1]=σ(z1[1])a^{[1]}_1 = \sigma(z^{[1]}_1)
z^{[1]}_2=w^{[1]T}+b^{[1]}_2
z2[1]=w[1]T+b2[1]z^{[1]}_2=w^{[1]T}+b^{[1]}_2
a^{[1]}_2 = \sigma(z^{[1]}_2)
a2[1]=σ(z2[1])a^{[1]}_2 = \sigma(z^{[1]}_2)
z^{[1]}_3=w^{[1]T}+b^{[1]}_3
z3[1]=w[1]T+b3[1]z^{[1]}_3=w^{[1]T}+b^{[1]}_3
a^{[1]}_3 = \sigma(z^{[1]}_3)
a3[1]=σ(z3[1])a^{[1]}_3 = \sigma(z^{[1]}_3)
z^{[2]}_1=w^{[2]T}+b^{[2]}_1
z1[2]=w[2]T+b1[2]z^{[2]}_1=w^{[2]T}+b^{[2]}_1
a^{[2]}_1 = \sigma(z^{[2]}_1)
a1[2]=σ(z1[2])a^{[2]}_1 = \sigma(z^{[2]}_1)
W^{[1]}
W[1]W^{[1]}
b^{[1]}
b[1]b^{[1]}
W^{[2]}
W[2]W^{[2]}
b^{[2]}
b[2]b^{[2]}
J(W^{[1]}, b^{[1]}, W^{[2]}, b^{[2]})
J(W[1],b[1],W[2],b[2])J(W^{[1]}, b^{[1]}, W^{[2]}, b^{[2]})
= \frac{1}{m} \sum
=1m∑= \frac{1}{m} \sum

Our Parameters

x_1
x1x_1
x_2
x2x_2
x_3
x3x_3
\hat{y}
y^\hat{y}
z^{[1]}_1=w^{[1]T}+b^{[1]}_1
z1[1]=w[1]T+b1[1]z^{[1]}_1=w^{[1]T}+b^{[1]}_1
a^{[1]}_1 = \sigma(z^{[1]}_1)
a1[1]=σ(z1[1])a^{[1]}_1 = \sigma(z^{[1]}_1)
z^{[1]}_2=w^{[1]T}+b^{[1]}_2
z2[1]=w[1]T+b2[1]z^{[1]}_2=w^{[1]T}+b^{[1]}_2
a^{[1]}_2 = \sigma(z^{[1]}_2)
a2[1]=σ(z2[1])a^{[1]}_2 = \sigma(z^{[1]}_2)
z^{[1]}_3=w^{[1]T}+b^{[1]}_3
z3[1]=w[1]T+b3[1]z^{[1]}_3=w^{[1]T}+b^{[1]}_3
a^{[1]}_3 = \sigma(z^{[1]}_3)
a3[1]=σ(z3[1])a^{[1]}_3 = \sigma(z^{[1]}_3)
z^{[2]}_1=w^{[2]T}+b^{[2]}_1
z1[2]=w[2]T+b1[2]z^{[2]}_1=w^{[2]T}+b^{[2]}_1
a^{[2]}_1 = \sigma(z^{[2]}_1)
a1[2]=σ(z1[2])a^{[2]}_1 = \sigma(z^{[2]}_1)
W^{[1]}
W[1]W^{[1]}
b^{[1]}
b[1]b^{[1]}
W^{[2]}
W[2]W^{[2]}
b^{[2]}
b[2]b^{[2]}
J(W^{[1]}, b^{[1]}, W^{[2]}, b^{[2]})
J(W[1],b[1],W[2],b[2])J(W^{[1]}, b^{[1]}, W^{[2]}, b^{[2]})
= \frac{1}{m} \sum^{m}_{i=1}
=1m∑i=1m= \frac{1}{m} \sum^{m}_{i=1}

Our Parameters

x_1
x1x_1
x_2
x2x_2
x_3
x3x_3
\hat{y}
y^\hat{y}
z^{[1]}_1=w^{[1]T}+b^{[1]}_1
z1[1]=w[1]T+b1[1]z^{[1]}_1=w^{[1]T}+b^{[1]}_1
a^{[1]}_1 = \sigma(z^{[1]}_1)
a1[1]=σ(z1[1])a^{[1]}_1 = \sigma(z^{[1]}_1)
z^{[1]}_2=w^{[1]T}+b^{[1]}_2
z2[1]=w[1]T+b2[1]z^{[1]}_2=w^{[1]T}+b^{[1]}_2
a^{[1]}_2 = \sigma(z^{[1]}_2)
a2[1]=σ(z2[1])a^{[1]}_2 = \sigma(z^{[1]}_2)
z^{[1]}_3=w^{[1]T}+b^{[1]}_3
z3[1]=w[1]T+b3[1]z^{[1]}_3=w^{[1]T}+b^{[1]}_3
a^{[1]}_3 = \sigma(z^{[1]}_3)
a3[1]=σ(z3[1])a^{[1]}_3 = \sigma(z^{[1]}_3)
z^{[2]}_1=w^{[2]T}+b^{[2]}_1
z1[2]=w[2]T+b1[2]z^{[2]}_1=w^{[2]T}+b^{[2]}_1
a^{[2]}_1 = \sigma(z^{[2]}_1)
a1[2]=σ(z1[2])a^{[2]}_1 = \sigma(z^{[2]}_1)
W^{[1]}
W[1]W^{[1]}
b^{[1]}
b[1]b^{[1]}
W^{[2]}
W[2]W^{[2]}
b^{[2]}
b[2]b^{[2]}
J(W^{[1]}, b^{[1]}, W^{[2]}, b^{[2]})
J(W[1],b[1],W[2],b[2])J(W^{[1]}, b^{[1]}, W^{[2]}, b^{[2]})
= \frac{1}{m} \sum^{m}_{i=1} L(\hat{y}, y)
=1m∑i=1mL(y^,y)= \frac{1}{m} \sum^{m}_{i=1} L(\hat{y}, y)
a^{[2]}
a[2]a^{[2]}

Now we need to calculate the derivatives - we must go backwards

Note: from now on we shall use the vectorized formulas

Summary: Vecorized Forward propagation

X

W

b

z=W^T+b
z=WT+bz=W^T+b
\hat{y} = a = \sigma(z)
y^=a=σ(z)\hat{y} = a = \sigma(z)
L(\hat{y}, y) = L(a, y)
L(y^,y)=L(a,y)L(\hat{y}, y) = L(a, y)

Summary: Vecorized Forward propagation

x_1
x1x_1
x_2
x2x_2
x_3
x3x_3
\hat{y}
y^\hat{y}
z^{[1]}_1=w^{[1]T}+b^{[1]}_1
z1[1]=w[1]T+b1[1]z^{[1]}_1=w^{[1]T}+b^{[1]}_1
a^{[1]}_1 = \sigma(z^{[1]}_1)
a1[1]=σ(z1[1])a^{[1]}_1 = \sigma(z^{[1]}_1)
z^{[1]}_2=w^{[1]T}+b^{[1]}_2
z2[1]=w[1]T+b2[1]z^{[1]}_2=w^{[1]T}+b^{[1]}_2
a^{[1]}_2 = \sigma(z^{[1]}_2)
a2[1]=σ(z2[1])a^{[1]}_2 = \sigma(z^{[1]}_2)
z^{[1]}_3=w^{[1]T}+b^{[1]}_3
z3[1]=w[1]T+b3[1]z^{[1]}_3=w^{[1]T}+b^{[1]}_3
a^{[1]}_3 = \sigma(z^{[1]}_3)
a3[1]=σ(z3[1])a^{[1]}_3 = \sigma(z^{[1]}_3)
z^{[2]}_1=w^{[2]T}+b^{[2]}_1
z1[2]=w[2]T+b1[2]z^{[2]}_1=w^{[2]T}+b^{[2]}_1
a^{[2]}_1 = \sigma(z^{[2]}_1)
a1[2]=σ(z1[2])a^{[2]}_1 = \sigma(z^{[2]}_1)
Z^{[1]} = W^{[1]}X + b^{[1]}
Z[1]=W[1]X+b[1]Z^{[1]} = W^{[1]}X + b^{[1]}
A^{[1]} = g^{[1]}[Z^{[1]}]
A[1]=g[1][Z[1]]A^{[1]} = g^{[1]}[Z^{[1]}]
Z^{[2]} = W^{[2]}A^{[1]} + b^{[2]}
Z[2]=W[2]A[1]+b[2]Z^{[2]} = W^{[2]}A^{[1]} + b^{[2]}
A^{[2]} = g^{[2]}[Z^{[2]}]
A[2]=g[2][Z[2]]A^{[2]} = g^{[2]}[Z^{[2]}]

Summary: Vecorized backward propagation

x

w

b

z=w^T+b
z=wT+bz=w^T+b
\hat{y} = a = \sigma(z)
y^=a=σ(z)\hat{y} = a = \sigma(z)
L(\hat{y}, y) = L(a, y)
L(y^,y)=L(a,y)L(\hat{y}, y) = L(a, y)

Summary: Vecorized backward propagation

x_1
x1x_1
x_2
x2x_2
x_3
x3x_3
\hat{y}
y^\hat{y}
z^{[1]}_1=w^{[1]T}+b^{[1]}_1
z1[1]=w[1]T+b1[1]z^{[1]}_1=w^{[1]T}+b^{[1]}_1
a^{[1]}_1 = \sigma(z^{[1]}_1)
a1[1]=σ(z1[1])a^{[1]}_1 = \sigma(z^{[1]}_1)
z^{[1]}_2=w^{[1]T}+b^{[1]}_2
z2[1]=w[1]T+b2[1]z^{[1]}_2=w^{[1]T}+b^{[1]}_2
a^{[1]}_2 = \sigma(z^{[1]}_2)
a2[1]=σ(z2[1])a^{[1]}_2 = \sigma(z^{[1]}_2)
z^{[1]}_3=w^{[1]T}+b^{[1]}_3
z3[1]=w[1]T+b3[1]z^{[1]}_3=w^{[1]T}+b^{[1]}_3
a^{[1]}_3 = \sigma(z^{[1]}_3)
a3[1]=σ(z3[1])a^{[1]}_3 = \sigma(z^{[1]}_3)
z^{[2]}_1=w^{[2]T}+b^{[2]}_1
z1[2]=w[2]T+b1[2]z^{[2]}_1=w^{[2]T}+b^{[2]}_1
a^{[2]}_1 = \sigma(z^{[2]}_1)
a1[2]=σ(z1[2])a^{[2]}_1 = \sigma(z^{[2]}_1)
dZ^{[2]} = A^{[2]} - Y
dZ[2]=A[2]−YdZ^{[2]} = A^{[2]} - Y
dW^{[2]} = \frac{1}{m}dZ^{[2]}A^{[1]T}
dW[2]=1mdZ[2]A[1]TdW^{[2]} = \frac{1}{m}dZ^{[2]}A^{[1]T}
db^{[2]} \approx \frac{1}{m}dZ^{[2]}
db[2]≈1mdZ[2]db^{[2]} \approx \frac{1}{m}dZ^{[2]}
dZ^{[1]} = W^{[2]T}dZ^{[2]}*g^{[1]}(Z{[1]})
dZ[1]=W[2]TdZ[2]∗g[1](Z[1])dZ^{[1]} = W^{[2]T}dZ^{[2]}*g^{[1]}(Z{[1]})
dW^{[1]} = \frac{1}{m}dZ^{[1]}X^{T}
dW[1]=1mdZ[1]XTdW^{[1]} = \frac{1}{m}dZ^{[1]}X^{T}
db^{[1]} \approx \frac{1}{m}dZ^{[1]}
db[1]≈1mdZ[1]db^{[1]} \approx \frac{1}{m}dZ^{[1]}

Last tip: randomly initialize the values of W and b.

<3

Canada

\alpha ?
α?\alpha ?

Will the gradient always work?

What's the best activation function?

How many hidden layers should I have?

Agenda

  1. Why is deep learning so popular now?
  2. Introduction to Machine Learning
  3. Introduction to Neural Networks
  4. Deep Neural Networks
  5. Training and measuring the performance of the N.N.
  6. Regularization
  7. Creating Deep Learning Projects
  8. CNNs and RNNs
  9. (OPTIONAL): Tensorflow intro
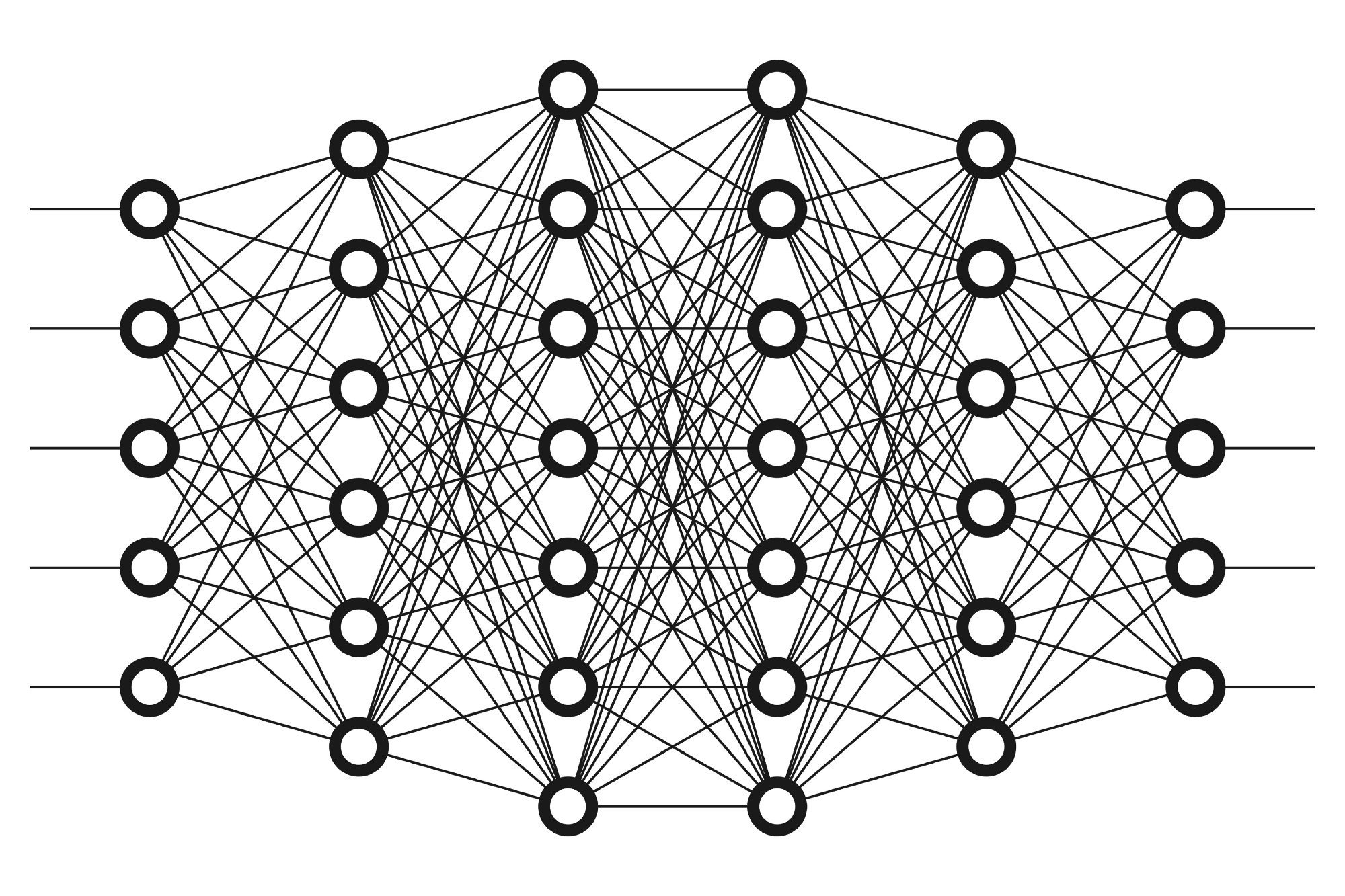
Source: https://medium.freecodecamp.org/want-to-know-how-deep-learning-works-heres-a-quick-guide-for-everyone-1aedeca88076
x_1
x1x_1
x_2
x2x_2
x_3
x3x_3
x_4
x4x_4
x_5
x5x_5
\hat{y}
y^\hat{y}

6 Layers; L=6

n^{[l]}
n[l]n^{[l]}

=number of units in a layer L

n^{[1]}=6
n[1]=6n^{[1]}=6
n^{[2]}=7
n[2]=7n^{[2]}=7
n^{[3]}=7
n[3]=7n^{[3]}=7
n^{[4]}=6
n[4]=6n^{[4]}=6
n^{[5]}=5
n[5]=5n^{[5]}=5
n^{[6]}=1
n[6]=1n^{[6]}=1
n^{[0]}=5
n[0]=5n^{[0]}=5

What should we compute in each of these layers L?

1. Forward step: Z and A

General idea

Z^{[l]} = W^{[l]}A^{[l-1]} + b^{[l]}
Z[l]=W[l]A[l−1]+b[l]Z^{[l]} = W^{[l]}A^{[l-1]} + b^{[l]}
A^{[l]} = g^{[l]}(Z^{[l]})
A[l]=g[l](Z[l])A^{[l]} = g^{[l]}(Z^{[l]})

Input:

A^{[l-1]}
A[l−1]A^{[l-1]}

Output:

A^{[l]}
A[l]A^{[l]}

Z works like a cache

2. Backpropagation: derivatives

General idea

Input:

dA^{[l]}
dA[l]dA^{[l]}

Output:

dA^{[l-1]}, dW{[l]}
dA[l−1],dW[l]dA^{[l-1]}, dW{[l]}
db{[l]}
db[l]db{[l]}

Basic building block

In a layer l,

Forward

Backprop

A^{[l-1]}
A[l−1]A^{[l-1]}
A^{[l]}
A[l]A^{[l]}
W^{[l]}
W[l]W^{[l]}
b^{[l]}
b[l]b^{[l]}
cache Z^{[l]}
cacheZ[l]cache Z^{[l]}
dA^{[l]}
dA[l]dA^{[l]}
dA^{[l-1]}
dA[l−1]dA^{[l-1]}
dZ^{[l]}
dZ[l]dZ^{[l]}
dW^{[l]} , db^{[l]}
dW[l],db[l]dW^{[l]} , db^{[l]}

<3

Canada

My predictions are awful. HELP

Agenda

  1. Why is deep learning so popular now?
  2. Introduction to Machine Learning
  3. Introduction to Neural Networks
  4. Deep Neural Networks
  5. Training and measuring the performance of the N.N.
  6. Regularization
  7. Creating Deep Learning Projects
  8. CNNs and RNNs
  9. (OPTIONAL): Tensorflow intro

When should I stop training? 

Select a fraction of your data set to check which model performs best.

Once you find the best model, make a final test (unbiased estimate)

Data

Training set

C.V. = Cross Validation set (select the best model)

C.V.

T = Test set (unbiased estimate)

T

Problem

h(x) = \theta_0 + \theta_1x
h(x)=θ0+θ1xh(x) = \theta_0 + \theta_1x

Does it look good?

Underfitting

h(x) = \theta_0 + \theta_1x
h(x)=θ0+θ1xh(x) = \theta_0 + \theta_1x

The predicted output is not even fitting the training data!

Problem

h(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4
h(x)=θ0+θ1x+θ2x2+θ3x3+θ4x4h(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4

Does it look good?

Overfitting

h(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4
h(x)=θ0+θ1x+θ2x2+θ3x3+θ4x4h(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4

The model fits everything

[Over, Under]fitting are problems related to the capacity

Capacity: Ability to fit a wide variety of functions

Overfitting

Underfitting

[Over, Under]fitting are problems related to the capacity

Capacity: Ability to fit a wide variety of functions

High variance

High Bias

How can we properly identify bias and variance problems?

A: check the error rates of the training and C.V. sets

Training set error 1%
C.V. Error 11%

High variance problem

Training set error 15%
C.V. Error 16%

High bias problem

(not even fitting the training set properly!)

Training set error 15%
C.V. Error 36%

High bias problem AND high variance problem

How can we control the capacity?

Are you fitting the data of the training set?

No

High bias

Bigger network (more hidden layers and units)

Train more

Different N.N. architecture

Yes

Is your C.V. error low?

No

High variance

More data

Regularization

Different N.N. architecture

Yes

DONE!

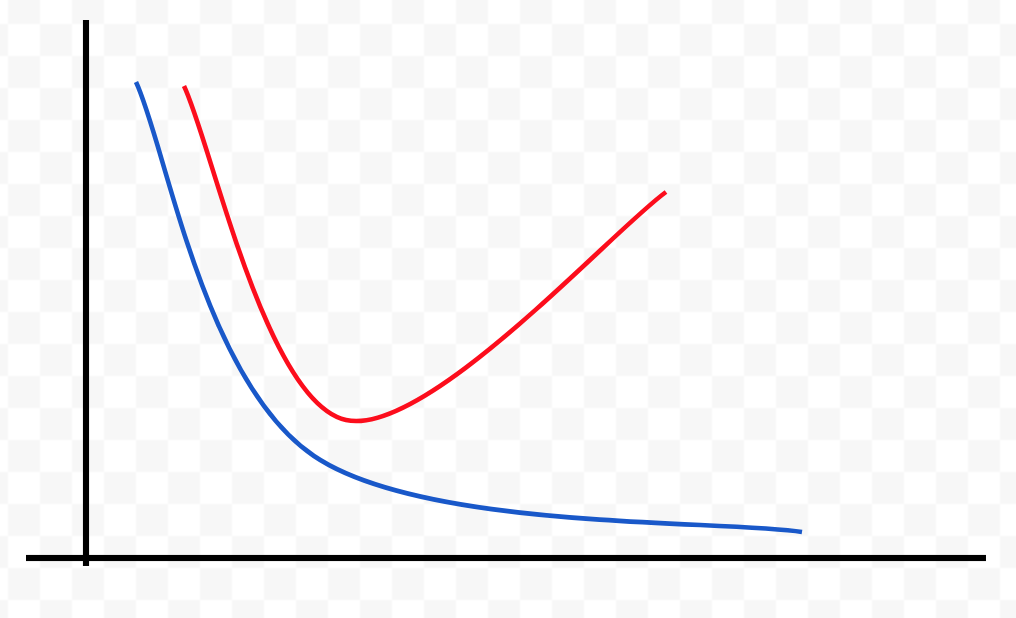
Error

Capacity

J(θ) test error

J(θ) train error

Error

Capacity

J(θ) cv error

J(θ) train error

Bias problem (underfitting)

J(θ) train error is high

J(θ) train ≈ J(θ) cv

J(θ) train error is low

J(θ) cv >> J(θ) train

Variance problem (overfitting)

Error

Capacity

J(θ) test error

J(θ) train error

Stop here!

Let's talk about overfitting

Why does it happen?

You end up having a very complex N.N., with the elements of the matrix W being too large. 

x_1
x1x_1
x_2
x2x_2
x_3
x3x_3
\hat{y}
y^\hat{y}

w: HIIIIIIIIIIIIIIIIII

w: HELOOO

w: WOAHHH

w: !!111!!!

W's with a strong presence in every layer can cause overfitting. How can we solve that?

x_1
x1x_1
x_2
x2x_2
x_3
x3x_3
\hat{y}
y^\hat{y}

w: HIIIIIIIIIIIIIIIIII

w: HELOOO

w: WOAHHH

w: !!111!!!

\lambda
λ\lambda

SHH
HHHHHH

Who is 

\lambda ?
λ?\lambda ?

Agenda

  1. Why is deep learning so popular now?
  2. Introduction to Machine Learning
  3. Introduction to Neural Networks
  4. Deep Neural Networks
  5. Training and measuring the performance of the N.N.
  6. Regularization
  7. Creating Deep Learning Projects
  8. CNNs and RNNs
  9. (OPTIONAL): Tensorflow intro

Regularization paramter

\lambda
λ\lambda

It penalizes the W matrix for being too large.

\lambda
λ\lambda

In terms of mathematics, how does it happen? 

\lambda
λ\lambda
W^{[l]}
W[l]W^{[l]}
\lambda
λ\lambda
W^{[l]}
W[l]W^{[l]}

Norm

Norm

||W^{[l]}||^2
∣∣W[l]∣∣2||W^{[l]}||^2

L2-Norm (Euclidean)

||W^{[l]}||
∣∣W[l]∣∣||W^{[l]}||

L1-Norm

{||W^{[l]}||}{^2}{_F}
∣∣W[l]∣∣2F{||W^{[l]}||}{^2}{_F}

Forbenius Norm

Final combo (L2-norm)

J(W^{[1]}, b^{[1]}, ..., W^{[l]}, b^{[l]}) =
J(W[1],b[1],...,W[l],b[l])=J(W^{[1]}, b^{[1]}, ..., W^{[l]}, b^{[l]}) =
\frac{1}{m} \sum^{m}_{i=1} L(\hat{y}, y)
1m∑i=1mL(y^,y) \frac{1}{m} \sum^{m}_{i=1} L(\hat{y}, y)
+\frac{\lambda}{2m}
+λ2m+\frac{\lambda}{2m}
||W^{[l]}||^2
∣∣W[l]∣∣2||W^{[l]}||^2
||W^{[l]}||^2 = \sum^{N_x}_{j=1} wj^2 = w^tw
∣∣W[l]∣∣2=∑j=1Nxwj2=wtw||W^{[l]}||^2 = \sum^{N_x}_{j=1} wj^2 = w^tw

<3

Canada

Are there other ways to perform regularization, without calculating a norm?

More slides here (Part II):

https://slides.com/hannelitavante-hannelita/deep-learning-unifei-ii#/

Deep Learning UNIFEI

By Hanneli Tavante (hannelita)

Deep Learning UNIFEI

  • 2,415

More from Hanneli Tavante (hannelita)