Montréal - October, 2017
Ideal Theory
in Rings
E. Noether, interpreted by @hannelita

TOO MANY QUESTIONS!!11
- What are ideals?
- What are rings?
- Who is E. Noether?
- Can we apply this weir mathematics to programming?
- Who are you?
Hi! I'm Hanneli (@hannelita)
- Computer Engineer
- Programming
- Electronics
- Math <3 <3
- Physics
- Lego
- Meetups
- Animals
- Coffee
- Pokémon
- GIFs
Disclaimer
- Tons of theory
- Mostly about Abstract Algebra...
- ... And many ppl are not familiar with this area
- I'll explain all the components we will need
- We'll see how to apply these concepts in programming
- TL;DR we will see some concepts that are not in the paper
- We won't cover 100% of the 51 pages of E. Noether's paper :')
- We will try to keep it simple, without much formalism from Mathematics [sorry!]
- GIFs will help us
The structure of this presentation
- Intro to Abstract Algebra
- Developing Abstract Algebra
- E. Noether
- The paper
- Applications
- Back to the paper
- References
A brief intro to Abstract Algebra
Groups



Groups
1. A set with an operation (any operation). Let's assume +.
2. This operation (+) is associative
3. For every element of this set (let's say a), there's a special element such that
(this special element is called identity element)
4. For element a in the set, there will be an inverse of a, denoted by
Groups
Formal notation: <G, +>
"Groups are abundant in nature" (PINTER, Charles).
Ex: the set of integers with respect to addition
Formal notation: <ℤ, +>
Ex: the set of integers with respect to multiplication
Formal notation: <ℤ, *>
Groups
Let's talk about *
The set of integers with respect to multiplication
Commutative property for the multiplication
It does not always happen!
If it does, we call the group a commutative group or abelian group
Groups
If it does, we call the group a commutative group or abelian group

Groups
If it does, we call the group a commutative group or abelian group

[Sub]Groups
If there is a subset S of a group G such that:
- The product of every element of S is in S (closed with respect to multiplication)
- S is closed with respect to inverses
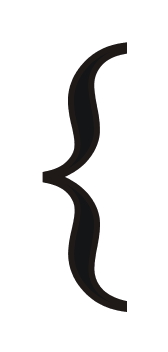
Or
- S is closed with respect to addition
- S is closed with respect to negatives
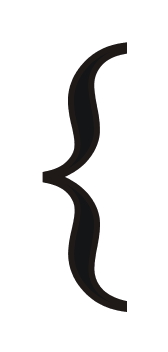
S is a subgroup of G
S is itself a Group!
This is too abstract (pun intended)
What can we classify as groups?
Interesting Groups
Imagine a group of... Functions
Group of all functions ℝ -> ℝ
Group of all continuous functions ℝ -> ℝ
Functions
A
B
a
b
c
x
y
z
Functions
A
B
a
b
c
x
y
z
f =
a b c
x y z
(
)
Bijective Function
f: A -> B
Domain
Image
Functions
Bijective Function
No remaining elements in the image
Only one arrow from one element in A to one in element in B
One-to-One function
Bijective functions have inverses
Important if we want to represent them as groups!
Functions
Bijective Function
No remaining elements in the image
Only one arrow from one element in A to one in element in B
One-to-One function
Bijective functions have inverses
Important if we want to represent them as groups!
Interesting Groups
Imagine a group of... a bijective function f: A->A
It rearranges the elements of A
Permutations of A
Examples: Set of the symmetries of a Square is a permutation group
Interesting Groups
Imagine a group of... a bijective function f: A->A
It rearranges the elements of A
Permutations of A
Examples: Set of the symmetries of a Square is a permutation group
a
b
d
c
a b c d
Interesting Groups
Imagine a group of... a bijective function f: A->A
It rearranges the elements of A
Permutations of A
Examples: Set of the symmetries of a Square is a permutation group
a
b
d
c
a b c d
Interesting Groups
Imagine a group of... a bijective function f: A->A
It rearranges the elements of A
Permutations of A
Examples: Set of the symmetries of a Square is a permutation group
d
a
c
b
a b c d
d a b c
Interesting Groups
Imagine a group of... a bijective function f: A->A
It rearranges the elements of A
Permutations of A
Examples: Set of the symmetries of a Square is a permutation group
a
b
d
c
a b c d
a d c b
Interesting Groups
Permutations are interesting
Interesting Groups
Permutations are interesting
f =
1 2 3 4 5 6 7 8 9
3 1 6 9 8 2 4 5 7
(
)
Interesting Groups
Permutations are interesting
f =
1 2 3 4 5 6 7 8 9
3 1 6 9 8 2 4 5 7
(
)
f =
1
3
6
2
Interesting Groups
Permutations are interesting
f =
1 2 3 4 5 6 7 8 9
3 1 6 9 8 2 4 5 7
(
)
f =
1
3
6
2
9
7
4
Interesting Groups
Permutations are interesting
f =
1 2 3 4 5 6 7 8 9
3 1 6 9 8 2 4 5 7
(
)
f =
1
3
6
2
9
7
4
8
5
Interesting Groups
Permutations are interesting
f =
1 2 3 4 5 6 7 8 9
3 1 6 9 8 2 4 5 7
(
)
f =
1
3
6
2
9
7
4
8
5
Cycles
GIF TIME

One important skill in programming is the ability to recognise the same structure in different scenarios
Two groups can be isomorphic!
There is a one-to-one correspondence which transforms one into another.
Another important skill is classifying
Another important skill is classifying
A1
A2
A3
A1, A2 and A3 are classes of a Partition of A
Two classes must be disjoint
The Union of these classes is the set A
If two classes are not disjoint, they are equal
Another important skill is classifying
A1
A2
A3
A1 ~ Ax
Ax
Ay
Az
A2 ~ Ay
A3 ~ Az
Equivalence Relation
We can have different partitions of the same set
Let's go back to groups
Even numbers are a subgroup of ℤ
- S is closed with respect to addition
- S is closed with respect to negatives
What about the odd numbers?
Zero is not part of the odd numbers 😱
The odd numbers are the even numbers shifted by one
odd = 2ℤ + 1
This is what we call...
Cosets
We have a group G and a subgroup H. For any element a in G,
aH denotes the set of all the products a*h; a remains fixed and h ranged all over H
For the previous example, we have H = <2ℤ,+>
Question: is aH == Ha ?
(Can we measure 'how commutative' a group is?)
hint:
(conjugate of a)
What happens if there's a function f that transforms one group (H) into another (G), but f is not a one-to-one correspondence?
f is a Homomorphism from H to G
Example:
What happens if there's a function f that transforms one group (H) into another (G), but f is not a one-to-one correspondence?
f is a Homomorphism from H to G
Example:
| + | e | o |
|---|---|---|
| e | e | o |
| o | o | e |
Parity group P
P is a homomorphic image of ℤ
P keeps one aspect of ℤ (odd of even)
Is there a way to construct all the homomorphic images of a group G?
Yes!
There's a particular type of subgroup, that
is closed with respect to products, inverses and conjugates
We call it normal subgroup of G (let's call it H)
The set that consists of all the cosets of H (let's call it G/H) is a homomorphic image of G.
GIF time!

We've been talking about groups for a while. It's time for a new character:
Rings
Similar to a group, but with two operations

Rings
Usually, the two operations are addition and multiplication
Every ring is a group
Properties of rings:
- a ring A with addition alone is an abelian group
- multiplication is associative
- multiplication is distributive over addition
Rings
Definition: Given the rings A and B, B absorbs products in A if we multiply an element i B by an element in A and the result is in B.
When a ring B is part of a larger ring A, B is a subring of A if B is closed with respect to addition, multiplication and negatives.
Rings
When multiplication is also commutative, we call it
A commutative ring
A ring does not necessarily have an identity element for multiplication
If there's one, we call it unity of A
And this is what we need to know to meet the next character:
Fields
(I'm sure we will survive to the formal definition)
A commutative ring,
with unity,
in which every nonzero element is invertible
Q, ℝ, C are examples of fields
Fields
Definition: A nonzero element is called divisor of zero if there's an element b in the ring such that the product a*b or b*a is equal to zero
Is ℤ a field?
Not really.
Property: A nonzero element a has an inverse such that
Fields
Definition: When there are no divisors of zero,
This is what we call cancellation property
So please give a warm welcome to...
=>
Fields
Integral domain
Commutative ring,
with unity,
having the cancellation property
And now, finally, the missing character:
Ideals
A nonempty subset B of a ring A
and B absorbs products in A
B is closed with respect to addition and negatives
Ideals are like normal subgroups for rings
Ideals

Normal subgroup: is closed with respect to products, inverses and conjugates
Ideals

Do you remember why we defined the normal subgroups?
Ideals

Because of the quotients. And guess what, if we had group quotients, then we have:
Ideals

Quotient rings!
Ideals
Ideals play an important role in abstract algebra; we can understand many properties of groups and fields just by analysing the ideals.
Mind-blowing questions
Abstraction is an important skill for programming
We saw many concepts in this talk
Concepts about... abstractions and generalisations
Who came up with these concepts?
1880 - 1930: E. Steinitz, David Hilbert, R. Dedekind, E. Artin, L. Kronecker, E. Kummer,
Emmy Noether
Emmy Noether (1882 - 1935)
Erlangen, Germany - 1907 she completes her studies in Mathematics
In 1915, D. Hilbert and F. Klein invite Noether to Göttingen
She did many works using Hilbert's name - women were not allowed to teach in some areas
She obtained a permission to teach in 1919 and stayed in Göttingen until 1933
"Ideal Theory in Rings" came in 1921
Now, the paper!
We already saw some definitions during the previous slides :)
It's mainly about ideals and rings
There are 12 sections. Let's go through them
Note: some definitions in the paper became obsolete
Keep alive: this will be a bit abstract (pun intended)
1. Ring, ideal, finiteness requirement
Definition of commutative ring,
integral domain,
and quotients
Ideals are always denoted by capital letters
Theorem of finite chain - infinite set of ideals, in which each ideal is divisible for the following one
2. Representation of an ideal as the least common multiple of finitely many irreducible ideals
Least common multiple of a ideals B1, B2,...,B2 is itself an ideal
Decomposing an ideal
There are reducible ideals (can be expressed as the least common multiple of proper divisors) and irreducible ideals
3. Equality of the number of components in two different decompositions into irreducible ideals
The equality between ideals relies on the properties of reducibility
If the components of an ideal are collected into groups and if we obtain the least common multiple, then the resulting representation is reduced.
And then we can compare the ideals
4. Primary ideals. Uniqueness of the prime ideals belonging to two different decompositions into irreducible ideals.
Q is a proper ideal of a commutative ring A if
x*y is an element of Q
x or n^y are also elements of Q
Something interesting happens when the ring A contains all the multiples of a prime (and Q will be a prime ideal):
Prime ideals are also primary ideals
Primary ideals are irreducible
5. Representation of an ideal as the least common multiple of maximal primary ideals. Uniqueness of the associated prime ideals.
A prime ideal is irreducible
We can think of an ideal B containing primary ideals (It's a loop!)
But B itself won't be a primary ideal
6. Unique representation of an ideal as the least common multiple of relatively prime irreducible ideals.
Two ideals I, J of a commutative ring R
are relatively prime (or coprime)
if A+B=R
Every ideal can be uniquely expressed as the least common multiple of finitely many mutually relatively prime and relatively prime irreducible ideals
GIF time

Where can I apply that? -.-
Abstract algebra and Generic Programming
We can identify pieces of our code as elements of abstract algebra
Very simple example:
class BankAccount
withdraw and deposit
Are withdraw and deposit commutative?
balance = 500.00; withdraws 600.00; deposits 1000.00;
Abstract algebra and Generic Programming
We can identify pieces of our code as elements of abstract algebra
Very simple example:
class BankAccount
withdraw and deposit
Are withdraw and deposit commutative?
balance = 500.00; withdraws 600.00; deposits 1000.00;
The balance will be negative for a moment
Abstract algebra and Generic Programming
We can identify pieces of our code as elements of abstract algebra
Very simple example:
class BankAccount
withdraw and deposit
Are withdraw and deposit commutative?
balance = 500.00; deposits 1000.00; withdraws 600.00;
Abstract algebra and Generic Programming
We can also do a better refactor if we apply the concepts of abstract algebra
Imagine that you have similar functions, accepting different parameters but performing similar operations
Maybe we can generalize the function
(we can interpret this as a group or ring)
The properties of ideals are a good example of elements of abstract algebra that help us with abstractions in programming
Abstract algebra and Generic Programming
"From Mathematics to Generic Programming"; A. STEPANOV and D. ROSE
Free slides of the classes
Now back to the paper :)
7 + 8. Uniqueness of the isolated ideals + Unique representation of an ideal as the product of coprime irreducible ideals
E. Noether makes a distinction between relatively primes and coprimes, but nowadays we treat both as similar structures
Every ideal can be uniquely expressed as the product of finitely many pairwise coprime ans coprime irreducible ideals
Note: think of coprime irreducible ideas as functions that cannot be more generalised. They reached a form where you can't decompose them anymore
9. Development of the study of modules. Equality of the number of components in decompositions into irreducible modules
Let's meet another character:
Modules
A Ring and a Set walk into a bar
Each of them has a pair of operations
One of the operations takes an element of the ring and an element of the module and returns an element of the module
The underlying set of the module and its operation form a group
(page 37)
10. Special case of the polynomial ring
We can interpret polynomials within rings
Do you remember your school time? 'Polynomial factorisation', 'Irreducible polynomial fractions'
Ch. 10 shows some properties of polynomials rings
In programming, we could interpret a chain of actions/method calls as a polynomial
And use the ideas of abstract algebra
11+12. Examples of number theory and the theory of differential expressions + Example from elementary divisor theory
Applying abstract algebra in other areas of mathematics
Final Example - Functional Programming and Abstract Algebra
You have a set of batteries, and you know their voltage (example: 9V, 12V, 24V)
You don't have any instrument to measure the voltage in a certain time
You want to obtain a certain voltage in one of the batteries and you are allowed to transfer the charges from one to another
Example


9V
12V
One of the batteries must end up with 6V. What should we do?
Initial state - both discharged (B1: 0V; B2: 0V)
B1
B2
Fully charge B1 (B1: 9V; B2: 0V)
Transfer the charge of B1 to B2 (B1: 0V; B2: 9V)
Fully charge B1 (B1: 9V; B2: 9V)
Transfer the charge of B1 to B2 (B1: 6V; B2: 12V)
Some code with states
trait Transfer {
def change(state: State): State
}
case class Empty(battery: Int) extends Transfer {
def change(state: State) = state updated (battery, 0)
}
case class FullCharge(battery: Int) extends Transfer {
def change(state: State) = state updated (battery, voltages(battery))
}
case class Charge(from: Int, to: Int) extends Transfer {
def change(state: State) = {
val charge = state(from) min (voltages(to) - state(to))
state updated (from, state(from) - charge)
updated (to, state(to) + charge)
}
}We can think of a group
val transfers =
( for ( b <- batteries ) yield Empty(b)) ++
(for (b <- batteries) yield FullCharge(b)) ++
(for (from <- batteries; to <- batteries if from != to)
yield Charge(from, to))Operation: charge
Identity element: 0
Inverse: Discharge
We can think of a coset
val transfers =
( for ( b <- batteries ) yield Empty(b)) ++
(for (b <- batteries) yield FullCharge(b)) ++
(for (from <- batteries; to <- batteries if from != to)
yield Charge(from, to))B1: n*3V
B2: n*3V
We can think of a ring
The final answer is Vector
We can multiply an add the elements of this vector

Other applications of Abstract Algebra
Computational Complexity, Cryptography, Graph Theory, Computational Group Theory
Final considerations
I hope this presentation helped you to understand some concepts of Abstract Algebra
Also, I hope you all know one of the works of a great mathematician of the 19th century, Emmy Noether
And I hope you have enjoyed the GIFs!
There's a connection between this area and programming - and we have much work to do
References
Charles Pinter; "A book of Abstract Algebra"
A. Stepanov and D. Rose; "From Mathematics to Generic Programming"
Lectures from KTH institute
Interesting threads from MathExchange
Thank you :)
Questions?
hannelita@gmail.com
@hannelita

Ideal Theory in Rings
By Hanneli Tavante (hannelita)
Ideal Theory in Rings
- 1,709



