A Gentle Introduction to Recursion Schemes
Jean-Remi Desjardins - LambdaConf 2016
Outline
- Motivate it
- How it works
- Examples
- How to use it
Recursion Schemes

Outline
- Motivate it
- How it works
- Examples
- How to use it
- Filesystems
- Compilers
- JSON
- etc
Recursive Data Types
- while loops 💩
- ad hoc recursion 🙂
- recursion schemes 💪
How do we reason, transform, process recursive data?
define recursive algorithms once and for all
Recursion Schemes
define your recursive data types in fixed point style
case class CompositeTree[A](leftChild: A, rightChild: A)Benefits of Recursion Schemes
- define recursive algorithms only once
- decouple how a function recurses over data from what the function actually does
- avoid general recursion
- more concise and DRY code
Drawback:
- Arguably uglier data types
Example
Modeling a tournament
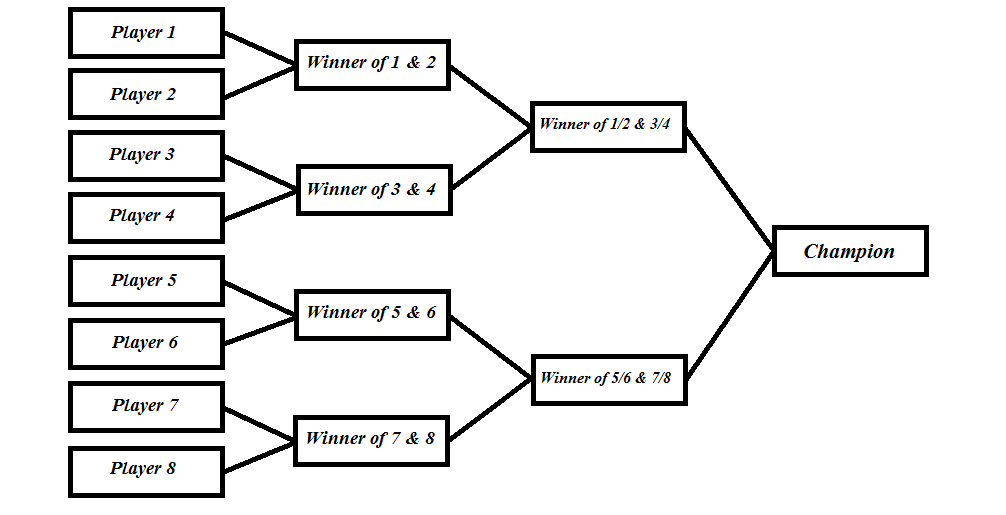
Initial Model
final class Participant(value: String) extends AnyVal
sealed trait Draw
case class FutureMatch(left: Draw, right: Draw) extends Draw
case class Match(left: Participant, right: Participant) extends Draw
Match
FutureMatch
Initial Model
final class Participant(value: String) extends AnyVal
sealed trait Draw
case class FutureMatch(left: Draw, right: Draw) extends Draw
case class Match(left: Participant, right: Participant) extends Drawdef size(d: Draw): Int = {
d match {
case Match(_,_) => 2
case FutureMatch(left, right) => size(left) + size(right)
}
}Fix Point Style
final class Participant(value: String) extends AnyVal
type Draw = Fix[DrawF]
sealed trait DrawF[A]
case class FutureMatchF[A](left: A, right: A) extends DrawF[A]
case class MatchF[A](left: Participant, right: Participant) extends DrawF[A]
Match
FutureMatch
Fix Point Style
def size(d: Draw): Int = {
d.cata {
case MatchF(_,_) => 2
case FutureMatchF(left, right) => left + right
}
}final class Participant(value: String) extends AnyVal
type Draw = Fix[DrawF]
sealed trait DrawF[A]
case class FutureMatchF[A](left: A, right: A) extends DrawF[A]
case class MatchF[A](left: Participant, right: Participant) extends DrawF[A]Initial model
sealed trait Draw
case class FutureMatch(left: Draw, right: Draw) extends Draw
case class Match(left: Participant, right: Participant) extends Draw// The participant in the draw with the best chance of winning the tournament
def bestChanceOfWinning(d: Draw): Task[Participant] = {
def bestChanceOfWinningR(d: Draw): Task[(Participant,Float)] =
d match {
case Match(left, right) => chanceOfWining(left, right).map(chance =>
if (chance > 0.5) (left, chance) else (right, (1 - chance))
)
case FutureMatch(left, right) =>
for {
left <- bestChanceOfWinningR(left)
(leftPart, leftChance) = left
right <- bestChanceOfWinningR(right)
(rightPart, rightChance) = right
chance <- chanceOfWining(leftPart, rightPart)
} yield {
val leftNewChance = leftChance * chance
val rightNewChance = rightChance * (1 - chance)
if (leftNewChance > rightNewChance) (leftPart, leftNewChance)
else (rightPart, rightNewChance)
}
}
bestChanceOfWinningR(d)._1
}def probabilityOfWin(candidate: Participant, over: Participant): Task[Float]Fixed Point Style
// The participant in the draw with the best chance of winning the tournament
def bestChanceOfWinning(d: Draw) =
d.cataM{
case MatchF(left, right) =>
chanceOfWining(left, right).map( chance =>
if (chance > 0.5) (left, chance) else (right, (1 - chance))
)
case FutureMatchF((leftPart, leftChance), (rightPart, rightChance)) =>
chanceOfWining(leftPart, rightPart).map { chance =>
val leftNewChance = leftChance * chance
val rightNewChance = rightChance * (1 - chance)
if (leftNewChance > rightNewChance) (leftPart, leftNewChance)
else (rightPart, rightNewChance)
}
}._1def probabilityOfWin(candidate: Participant, over: Participant): Task[Float]type Draw = Fix[DrawF]
sealed trait DrawF[A]
case class FutureMatchF[A](left: A, right: A) extends DrawF[A]
case class MatchF[A](left: Participant, right: Participant) extends DrawF[A]Comparison
def bestChanceOfWinning(d: Draw) =
d.cataM{
case FutureMatchF((leftPart, leftChance), (rightPart, rightChance)) =>
chanceOfWining(leftPart, rightPart).map { chance =>
val leftNewChance = leftChance * chance
val rightNewChance = rightChance * (1 - chance)
if (leftNewChance > rightNewChance) (leftPart, leftNewChance)
else (rightPart, rightNewChance)
}
}._1def bestChanceOfWinning(d: Draw): Task[Participant] = {
def bestChanceOfWinningR(d: Draw): Task[(Participant,Float)] =
d match {
case FutureMatch(left, right) =>
for {
left <- bestChanceOfWinningR(left)
(leftPart, leftChance) = left
right <- bestChanceOfWinningR(right)
(rightPart, rightChance) = right
chance <- chanceOfWining(leftPart, rightPart)
} yield {
val leftNewChance = leftChance * chance
val rightNewChance = rightChance * (1 - chance)
if (leftNewChance > rightNewChance) (leftPart, leftNewChance)
else (rightPart, rightNewChance)
}
}
bestChanceOfWinningR(d)._1
}One More Example -Unfolds
Initial Model - unfold
sealed trait Draw
case class FutureMatch(left: Draw, right: Draw) extends Draw
case class Match(left: Participant, right: Participant) extends Draw a match {
case xs if xs.size < 2 => None
case x1 :: x2 :: Nil => Some(Match(x1, x2))
case xs =>
val (left,right) = xs.split(xs.size / 2)
(fromList(left) ⊛ fromList(right))(FutureMatch)
}def fromList(a: List[Participant]): Option[Draw] =Fixed point style - unfold
Fix[DrawF].anaM(a){
case xs if xs.size < 2 => None
case x1 :: x2 :: Nil => Some(MatchF(x1,x2))
case xs =>
val (left,right) = xs.split(xs.size / 2)
Some(FutureMatchF(left,right))
}def fromList(a: List[Participant]): Option[Draw] =type Draw = Fix[DrawF]
sealed trait DrawF[A]
case class FutureMatchF[A](left: A, right: A) extends DrawF[A]
case class MatchF[A](left: Participant, right: Participant) extends DrawF[A]unfold comparison
def fromList(a: List[Participant]): Option[Draw] =
Fix[DrawF].anaM(a){
case xs if xs.size < 2 => None
case x1 :: x2 :: Nil => Some(MatchF(x1,x2))
case xs =>
val (left,right) = xs.split(xs.size / 2)
Some(FutureMatchF(left,right))
}def fromList(a: List[Participant]): Option[Draw] =
a match {
case xs if xs.size < 2 => None
case x1 :: x2 :: Nil => Some(Match(x1, x2))
case xs =>
val (left,right) = xs.split(xs.size / 2)
(fromList(left) ⊛ fromList(right))(FutureMatch)
}Intuition
sealed trait DrawF[A]
case class FutureMatchF[A](left: A, right: A) extends DrawF[A]
case class MatchF[A](left: Participant, right: Participant) extends DrawF[A]FutureMatch[Int] = FutureMatch(3,4)
FutureMatch[String] = FutureMatch("Bob", "Dylan")val draw: FutureMatch[Draw[Draw[Draw[...]]]] // How to model a recursive draw?Outline
- Motivate it
- How it works
- Examples
- How to use it
How it works
val draw: FutureMatch[Draw[Draw[Draw[...]]]] // How to model a recursive draw?final case class Fix[F[_]](unFix: F[Fix[F]]) {
def cata...
def cataM...
def ana...
def anaM...
...
}type Draw = Fix[DrawF]Theory:
- Fix is the Y combinator
- Fix[Draw] is the fixed point of the Draw functor
How it works
val draw: Fix[DrawF]
val futureMatch: FutureMatchF[Fix[DrawF]] = draw.unfix
val leftSide: Fix[DrawF] = futureMatch.left
val result: FutureMatchF[Fix[DrawF]] = leftSide.unfix
val result1: Fix[DrawF] = result.left
val result2: MatchF[Fix[Draw]] = result1.unfix
val leftParticipant: Participant = result2.leftAn instance of Functor is required
def cata[F[_]: Functor, A](t: T[F])(f: F[A] => A): A =
f(project(t) ∘ (cata(_)(f)))Outline
- Motivate it
- How it works
- Examples
- How to use it
AST Example (stolen from SumTypeOfWay)
data Expr
= Index Expr Expr
| Call Expr [Expr]
| Unary String Expr
| Binary Expr String Expr
| Paren Expr
| Literal Lit
deriving (Show, Eq)-- this would turn the expression
-- (((anArray[(10)])))
-- into
-- anArray[10]
flatten :: Expr -> Expr
flatten (Literal i) = Literal i
flatten (Paren e) = flatten e
flatten (Index e i) = Index (flatten e) (flatten i)
flatten (Call e args) = Call (flatten e) (map flatten args)
flatten (Unary op arg) = Unary op (flatten arg)
flatten (Binary l op r) = Binary (flatten l) op (flatten r)Fixed point stye
data Expr a
= Index a a
| Call [a]
| Unary String a
| Binary a String a
| Paren a
| Literal Lit
deriving (Show, Eq, Functor)-- this would turn the expression
-- (((anArray[(10)])))
-- into
-- anArray[10]
flatten :: Term Expr -> Term Expr
flatten (In (Paren e)) = e -- remove all Parens
flatten other = other -- do nothing otherwiseExample in Quasar
// final case class InvokeF[A](func: Func, values: List[A]) extends LogicalPlan[A]
def simpleEvaluation(lp: Fix[LogicalPlan]): FileSystemErrT[InMemoryFs, Vector[Data]] = {
val optLp = Optimizer.optimize(lp)
EitherT[InMemoryFs, FileSystemError, Vector[Data]](State.gets { mem =>
import quasar.LogicalPlan._
import quasar.std.StdLib.set.{Drop, Take}
import quasar.std.StdLib.identity.Squash
optLp.para[FileSystemError \/ Vector[Data]] {
case ReadF(path) =>
// Documentation on `QueryFile` guarantees absolute paths, so calling `mkAbsolute`
val aPath = mkAbsolute(rootDir, path)
fileL(aPath).get(mem).toRightDisjunction(pathErr(pathNotFound(aPath)))
case InvokeF(Drop, (_,src) :: (Fix(ConstantF(Data.Int(skip))),_) :: Nil) =>
src.flatMap(s => skip.safeToInt.map(s.drop).toRightDisjunction(unsupported(optLp)))
case InvokeF(Take, (_,src) :: (Fix(ConstantF(Data.Int(limit))),_) :: Nil) =>
src.flatMap(s => limit.safeToInt.map(s.take).toRightDisjunction(unsupported(optLp)))
case InvokeF(Squash,(_,src) :: Nil) => src
case ConstantF(data) => Vector(data).right
case other =>
queryResponsesL
.get(mem)
.mapKeys(Optimizer.optimize)
.get(Fix(other.map(_._1)))
.toRightDisjunction(unsupported(optLp))
}
})
}Example in Quasar
def para[F[_]: Functor, A](t: Fix[F])(f: F[(Fix[F], A)] => A): AOutline
- Motivate it
- How it works
- Examples
- How to use it
All the Recursions
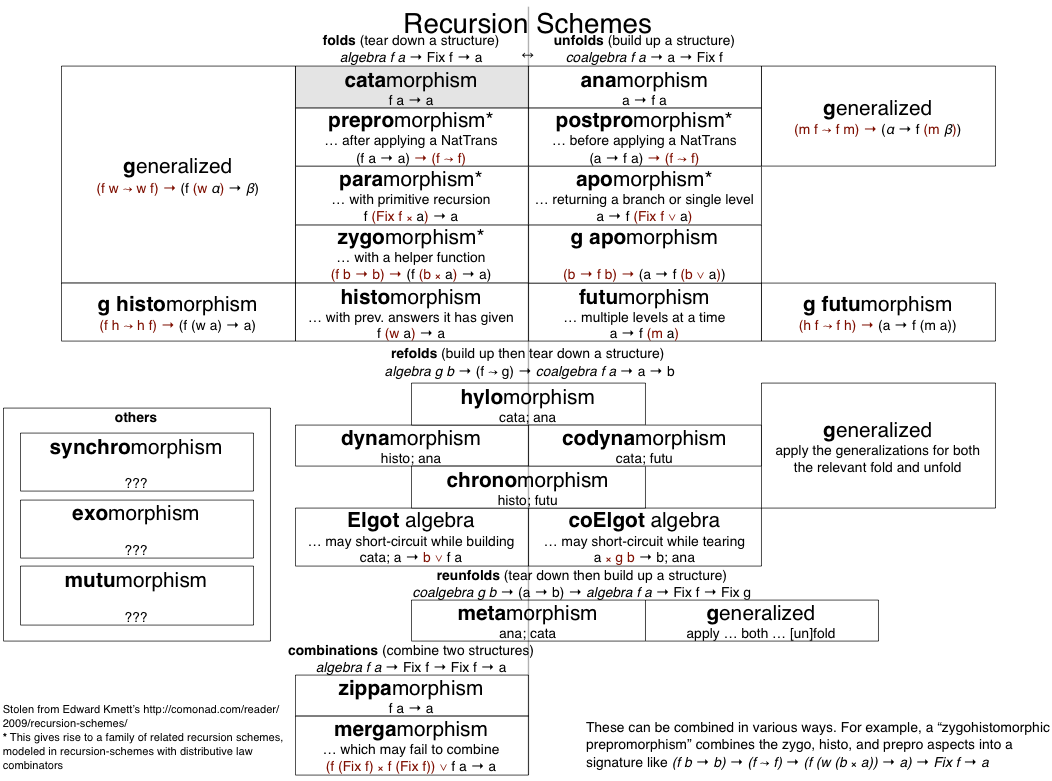
Matryoshka
libraryDependencies += "com.slamdata" %% "matryoshka-core" % "0.11.1"
Recursion Schemes (Haskell)

Acknowledgment
- Patrick Thomson - http://blog.sumtypeofway.com/an-introduction-to-recursion-schemes/
A Gentle Introduction to Recursion Schemes
By Jean-Rémi Desjardins
A Gentle Introduction to Recursion Schemes
Recursion Schemes, popularized by the notorious paper Functional Programming with Bananas, Lenses, Envelopes and Barbed Wire, is an very elegant technique for expressing recursive algorithms on arbitrarily nested data structures. This talk will offer a gentle introduction to the subject. We will begin by motivating its use and then follow through with some intuition for the concepts and finally walktrough some concrete examples. Only basic familiarity with functional programming abstractions will be assumed. The audience can expect to leave with a burning desire to write all their recursive data types in fixed point style.
- 1,255



