La loi binomiale
1. Répétition d’expériences identiques et indépendantes
1.1 Définition
-
Il y a répétition d’expériences identiques lorsque la même expérience aléatoire est répétée plusieurs fois, dans les mêmes conditions.
-
Des expériences aléatoires sont indépendantes si l’issue de l’une, quelconque, de ces expériences ne dépend pas de l’issue des autres expériences.
Exemple :
Une urne contient 4 boules rouges, 3 boules vertes et 2 boules noires. On tire successivement deux boules avec remise.
Il y a répétition de deux expériences identiques et indépendantes.
Remarque :
Si le tirage avait été sans remise, les expériences n’auraient été ni identiques (pas le même nombre de boules pour le deuxième tirage), ni indépendantes (la répartition des boules du deuxième tirage dépend de la couleur de la première boule tirée).
1.2 Modélisation d’une répétition
On utilise un arbre pondéré pour représenter cette répétition. Sur chaque branche, on indique la probabilité de l’issue correspondante.
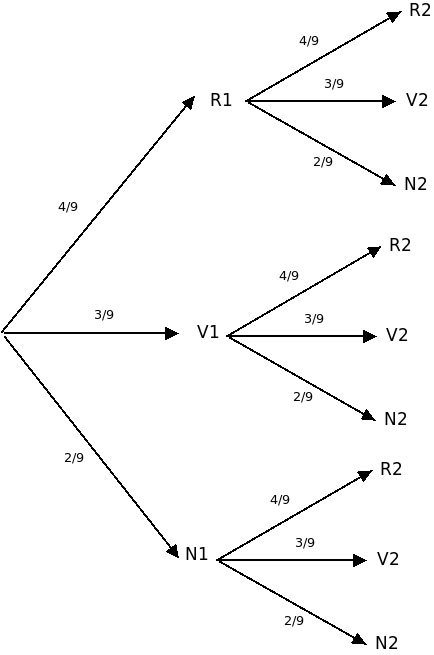
Propriété :
- La probabilité d’un événement sur l’arbre est obtenue en multipliant les probabilités portées sur ses branches.
- La probabilité d’un événement correspondant à plusieurs chemins est obtenue en ajoutant les probabilités de chaque chemin.
Exemple : On reprend l’exemple précédent.
- La probabilité de tirer une boule verte puis une boule rouge est :
- La probabilité de tirer deux boules de même couleur est :

2. Loi de Bernoulli
Définitions :
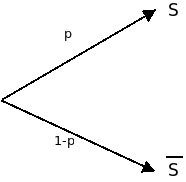
On appelle épreuve de Bernoulli toute épreuve à deux issues possibles : un succès (noté ) ou un échec (noté ).
La loi de Bernoulli est la loi de probabilité de la variable aléatoire (notée ici Y) prenant la valeur 1 si l’issue est un succès, et 0 si l’issue est un échec.
On note p, la probabilité d'un succès.
La variable aléatoire Y suit la loi de Bernoulli de paramètre p.
On note :
p = p (S) = p (Y = 1)
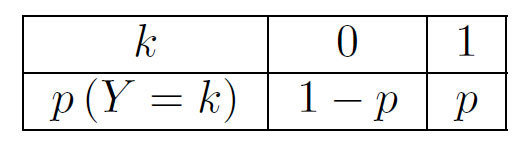
Exemple :
On lance un dé équilibré à six faces, les faces étant numérotées de 1 à 6. On considère qu’il y a un succès lorsque le résultat du lancer est un 6, un échec sinon.
Il s’agit d’une épreuve de Bernoulli de paramètre
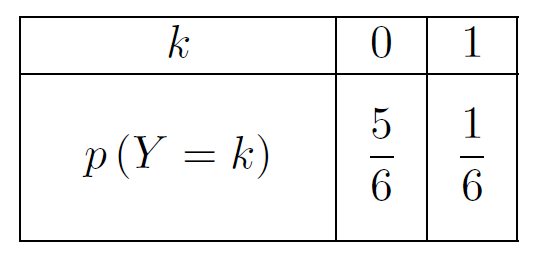
La variable aléatoire Y suit la loi de Bernoulli de paramètre
Propriété :
Soit Y une variable aléatoire suivant la loi de Bernoulli de paramètre p.
E (Y) = p et V (Y) = p(1 − p)
Démonstration :
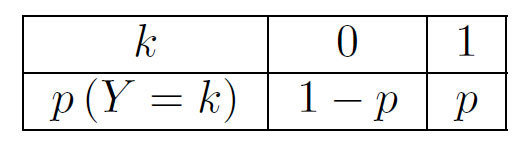
V (Y) = (1 − p) × (0 − E (Y))² + p × (1 − E(Y))²
= (1 − p) × p² + p × (1 − p)²
= p(1 − p) [p + 1 − p]
= p (1 − p)
3. Schéma de Bernoulli – Loi binomiale
3.1 Un exemple pour comprendre
On considère l’expérience aléatoire consistant à lancer trois fois de suite un dé à 6 faces non truqué.
La variable aléatoire X représente le nombre de fois où le numéro 6 est sorti au cours de ces 3 lancers.
On peut modéliser cette expérience par une répétition indépendante de l’épreuve de Bernoulli de l’exemple du 2. On obtient l’arbre pondéré suivant :
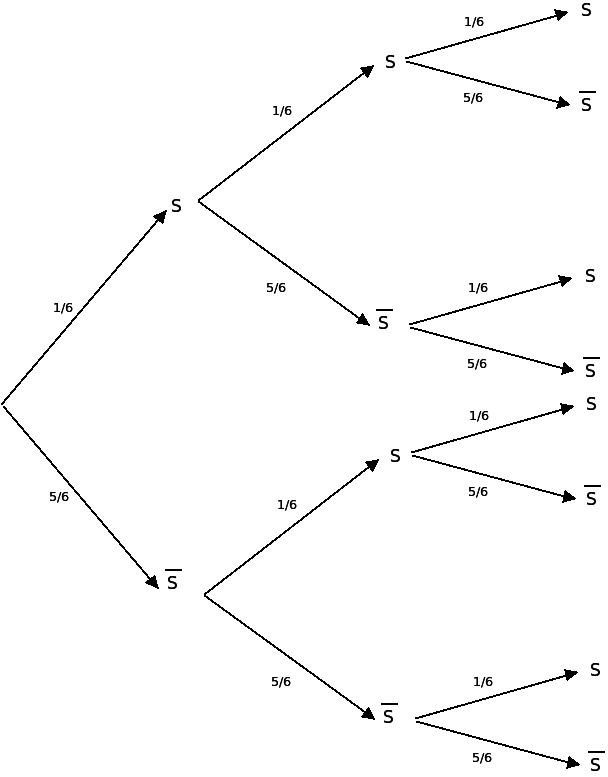
La variable aléatoire X peut prendre les valeurs 0, 1, 2 ou 3.
- X = 0 correspond à l’événement
- X = 1 correspond à l’événement
- X = 2 correspond à l’événement
- X = 3 correspond à l’événement
3.2 Schéma de Bernoulli – Loi binomiale
Définitions :
On appelle schéma de Bernoulli d’ordre n l’expérience consistant à répéter n fois de manière indépendante la même épreuve de Bernoulli de paramètre p.
On dit aussi que la variable aléatoire X suit la loi binomiale de paramètres n et p.
La loi binomiale de paramètres n et p est la loi de probabilité de la variable aléatoire X prenant comme valeurs le nombre de succès (S) obtenus au cours des n épreuves du schéma de Bernoulli.
Remarque :
Dans l’exemple du 3.1, on a donc un schéma de Bernoulli d’ordre 3.
La variable aléatoire X suit la loi binomiale de paramètres 3 et
Définition :
Le nombre de chemins de l’arbre pondéré associé à un schéma de Bernoulli d’ordre n conduisant à k succès pour n répétitions
est noté : (lire lit "k parmi n")
Les nombres entiers sont appelés coefficients binomiaux.
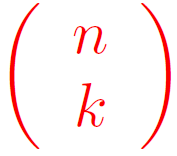
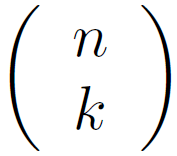
Remarque :
Grâce au 3.1, on a déjà trouvé que :
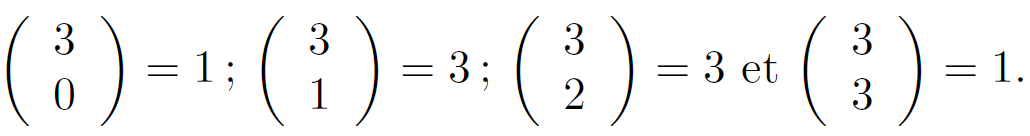
Propriété :
Soit X une variable aléatoire suivant la loi binomiale de paramètres n et p.
- Les valeurs de X sont {0 ; 1 ; 2 ; . . . ; n}.
- Pour tout k {0 ; 1 ; 2 ; . . . ; n} :
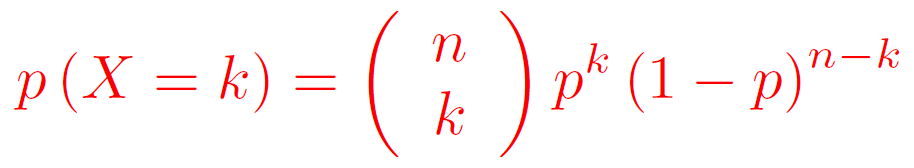
3.3 Espérance, variance, écart-type
Propriété : (admis)
Soit X une variable aléatoire suivant la loi binomiale de paramètres n et p.
Son espérance est :
Sa variance est :
Son écart-type est :
Loi binomiale & calculatrice.
Exemples d'utilisation de la calculatrice pour :
-
Afficher des coefficients binomiaux
-
Calculer des probabilités selon une loi binomiale
TP 23 page 334 (Transmath)
CASIO
TI

CASIO
TI

NUMWORKS
Dans tous les menus tapez paste
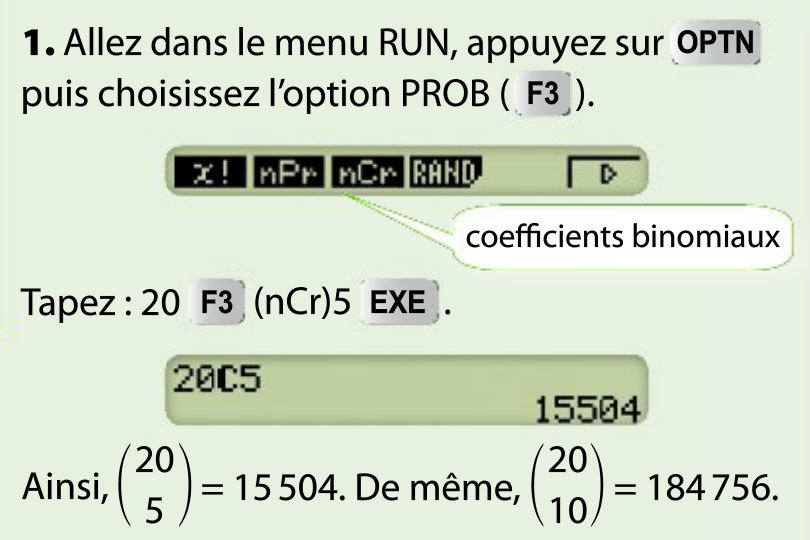
1. COEFFICIENTS BINOMIAUX

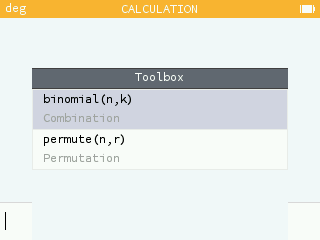
Le nombre de chemins menant à 5 succès dans un schéma de Bernoulli d'ordre n = 20 ( représenté par un arbre à 20 niveaux) est égal à 15504. Le nombre de chemins menant à 10 succès dans le même schéma est égal à 184756.

ou
2. PROBABILITÉS
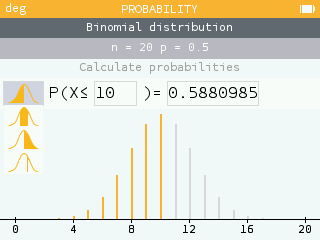
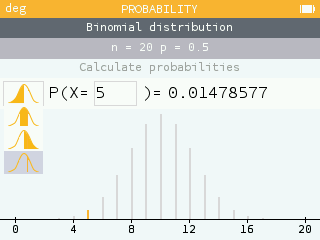

Une prise de commande est une épreuve de Bernoulli de paramètre p = 0,1.
Il y a une répétition de 8 épreuves de Bernoulli identiques et indépendantes donc c'est un schéma de Bernoulli d'ordre 8. X la variable aléatoire qui indique le nombre de commandes par jour suit donc la loi binomiale de paramètres n = 8 et p = 0,1.

a)
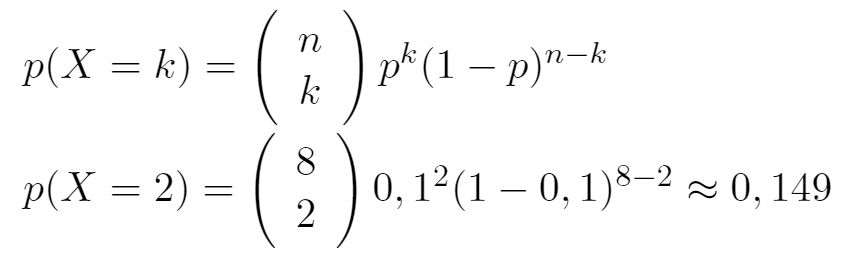
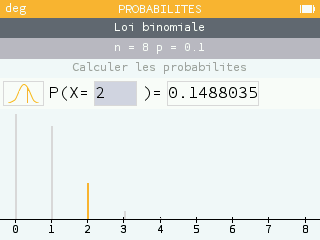
b)
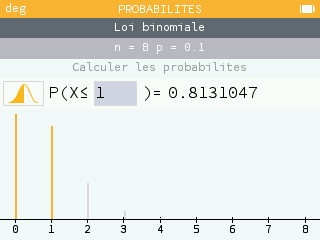
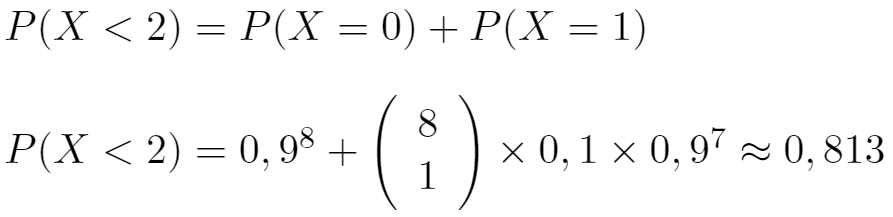

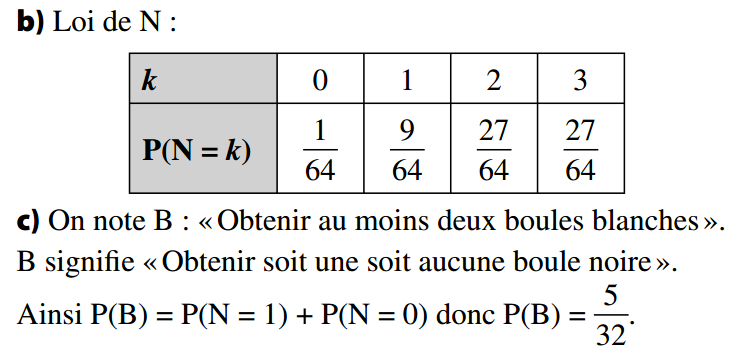
On note a le nombre de boules blanches.
L’urne contient a boules blanches et 3a boules noires.
D’où la probabilité de tirer une boule noire :

Un tirage est une épreuve de Bernoulli de paramètre p = 0,75.
Il y a une répétition de 3 tirages avec remise donc identiques et indépendants. L'expérience est un schéma de Bernoulli d'ordre 3. N la variable aléatoire qui indique le nombre de boules noires obtenues suit donc la loi binomiale de paramètres n = 3 et p = 0,75.

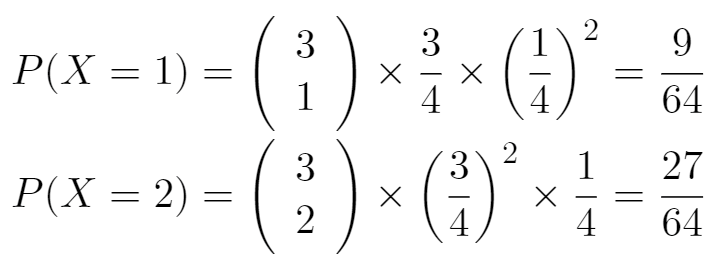







Le triangle de Pascal
Il permet de retrouver les premiers coefficients binomiaux :
1
1 2 1
}
Début du triangle
Ensuite on additionne selon cette règle :
b
c
1 3 3 1
+
+
1 4 6 4 1
1 5 10 10 5 1...
1 1
+
+
+
+
a
+
3.4 Compléments sur les coefficients binomiaux
Le triangle de Pascal
1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1...
1 1
0 1 2 3 4 5
k
0
1
2
3
4
5
n
"2 parmi 3 égal 3" : Il y a 3 chemins menant à 2 succès pour 3 répétitions.
Lecture des coefficients binomiaux :
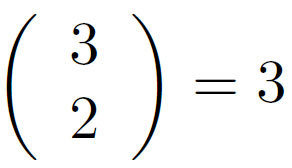
(k succès)
(n répétitions)
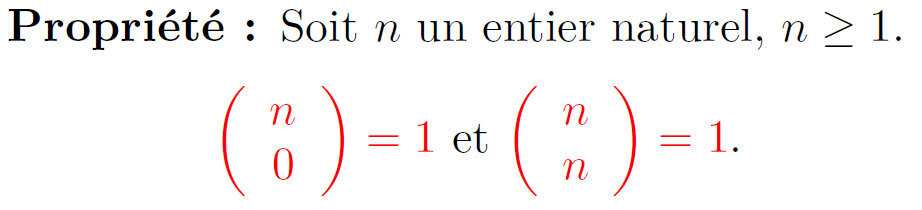
1 5 10 10 5 1
0 1 2 3 4 5
k
5
n
Exemples :


- Il n'existe qu'un chemin menant à 0 succès pour 5 répétitions
- Il n'existe qu'un chemin menant à 5 succès pour 5 répétitions

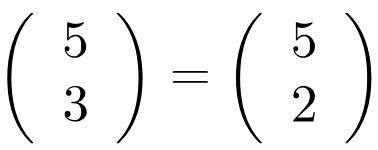
1 5 10 10 5 1
0 1 2 3 4 5
k
5
n
Exemple :
Démonstration :
Comme n − k succès correspondent à k échecs, il y a autant de chemins menant à k succès qu’à n − k succès.
Pour n= 5 et k = 2 :
Démonstration :
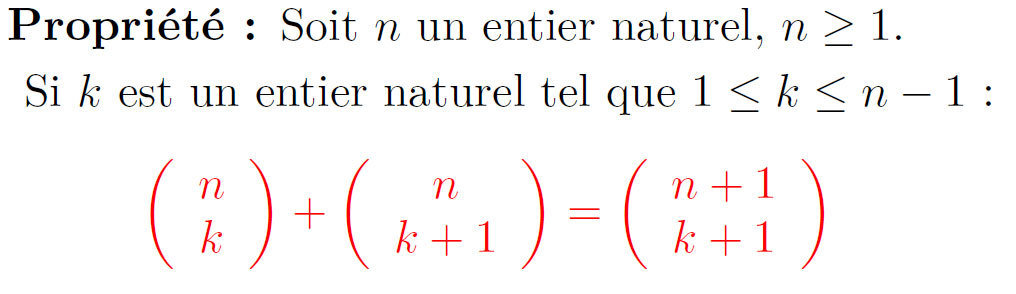

Remarque :
C'est cette propriété qui permet de compléter le triangle de Pascal.
b
c
a
n
k
n + 1
k + 1
Démonstration :
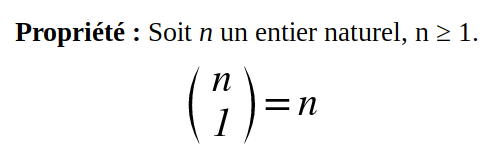
Il y a n chemins menant à un succès parmi n répétitions.
Exercices sur la loi binomiale








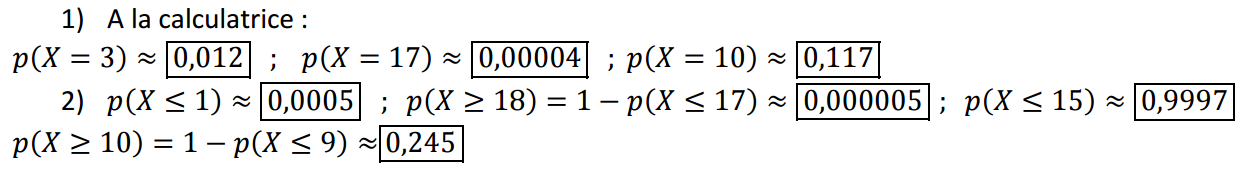
Exercices sur les coefficients binomiaux



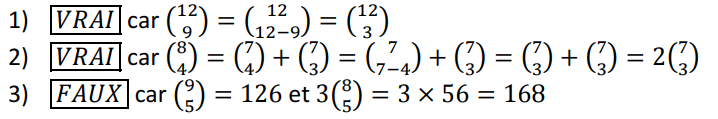
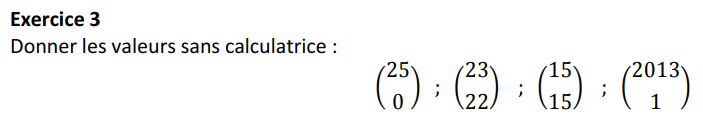
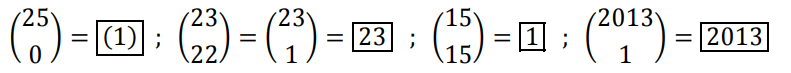




Représentation graphique de la loi binomiale
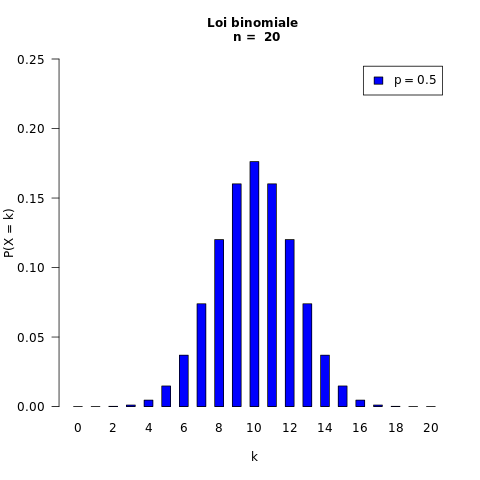
Exemple :
20 répétitions : n = 20
probabilité du succès : p = 0,5
La probabilité d'obtenir 8 succès pour 20 répétitions
est environ 0,12
le nombre de succès
En abscisse :
la probabilité
En ordonnée :
d'obtenir ce nombre de succès
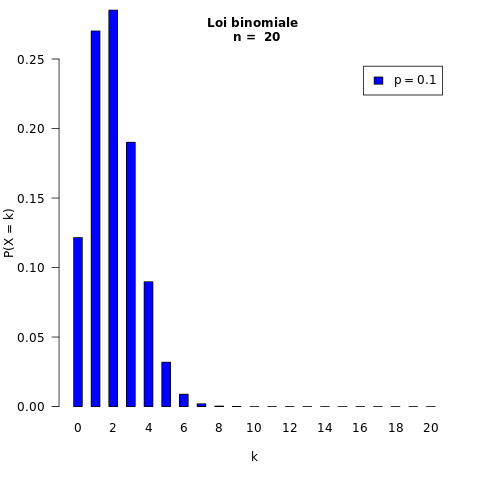
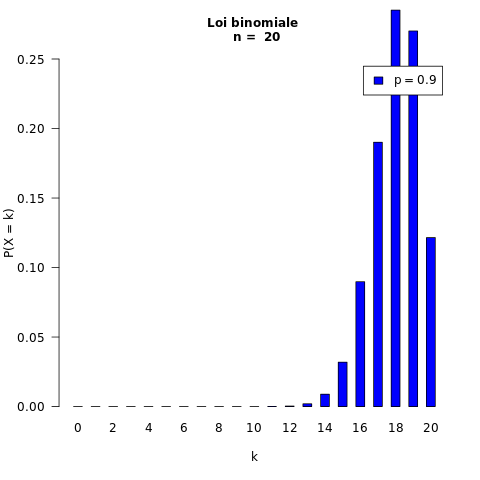
On fait varier p :
Exemples :
20 répétitions : n = 20
probabilité du succès : p = 0,1
20 répétitions : n = 20
probabilité du succès : p = 0,9


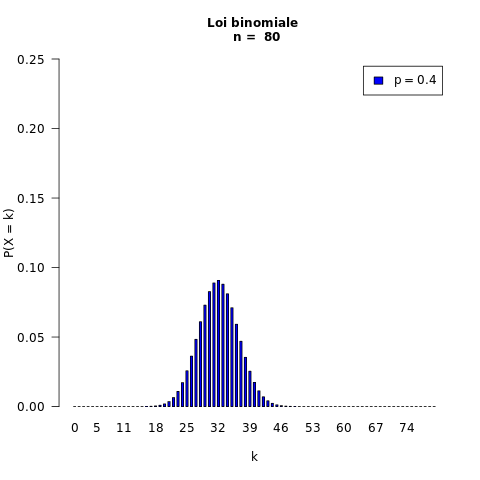
On fait varier n :
Exemples :
80 répétitions : n = 80
probabilité du succès : p = 0,4
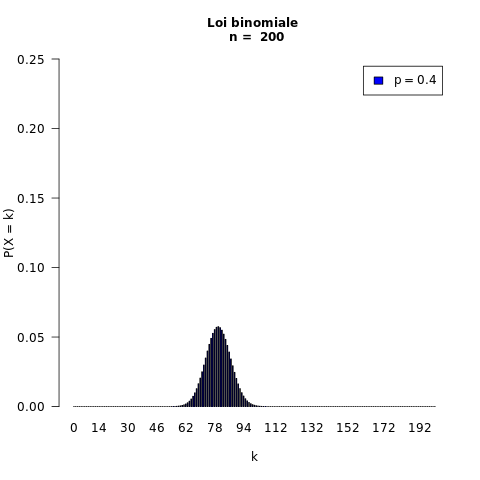
200 répétitions : n = 200
probabilité du succès : p = 0,4
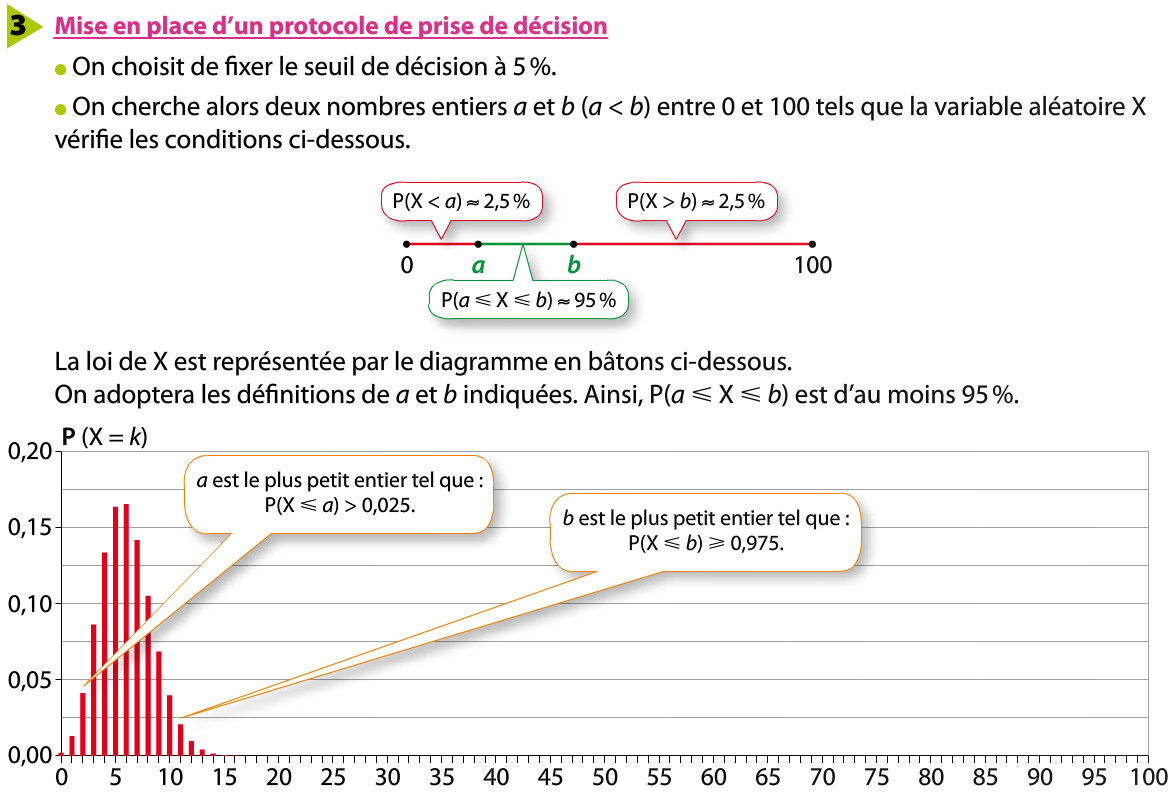
Act3 p 317 : Échantillonnage et prise de décision

Le médecin peut répondre par la négative. La fréquence observée laisse penser que la proportion d'habitants du Pays basque appartenant au groupe O- est plus importante que celle de la population globale française.


La probabilité d'avoir 19 personnes O- dans l'échantillon est très faible. On peut penser que l'hypothèse p = 0,06 est fausse.

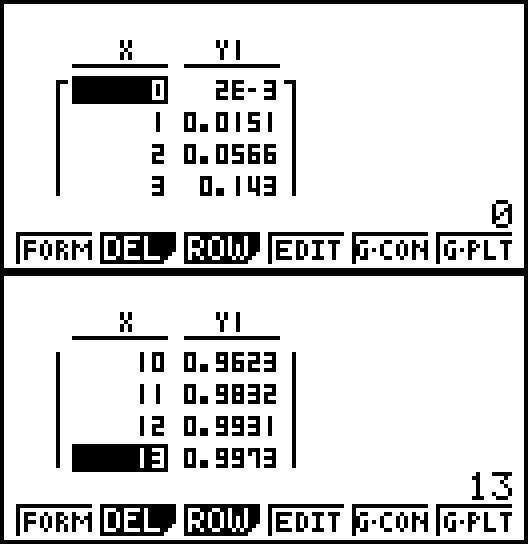
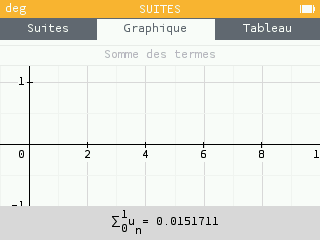
Sur NUMWORKS : Dans le menu suite entrer
puis Graphique OK Somme des termes
Sélectionner le premier terme : 0
Sélectionner le dernier terme : 0
Appuyer sur la flèche retour.
Sélectionner le dernier terme : 1
et ainsi de suite...
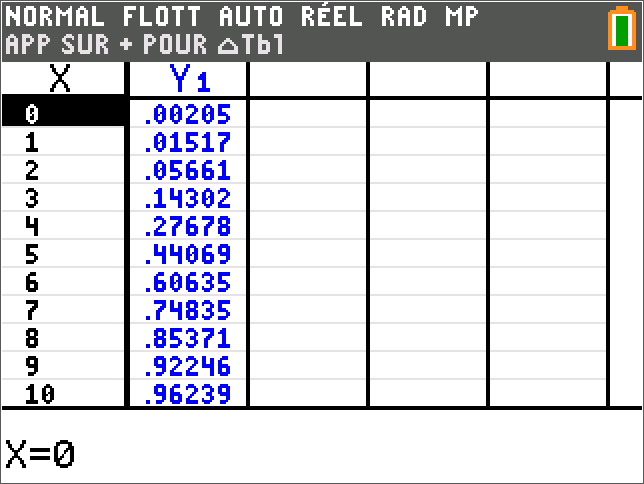
Sur CASIO : Dans le menu TABLE entrer Y=BinomialCD(X,100,.06)
Sur TI : Appuyer sur f(x) puis entrer Y=binomFRép(100,.06,X)

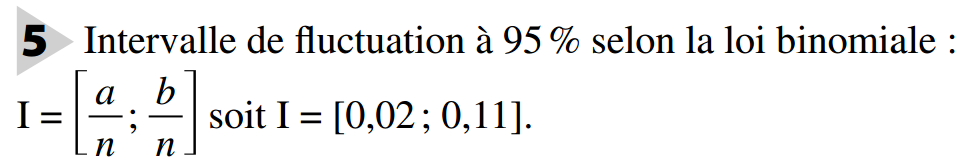


4. Intervalle de fluctuation et prise de décision
4.1 Quelques rappels de Seconde
Définitions :
- On appelle échantillon de taille n la série statistique formée des résultats obtenus lorsqu’on répète n fois une expérience dans les mêmes conditions.
- La distribution de fréquences associée à l’échantillon est le tableau des fréquences issues de cette échantillon.
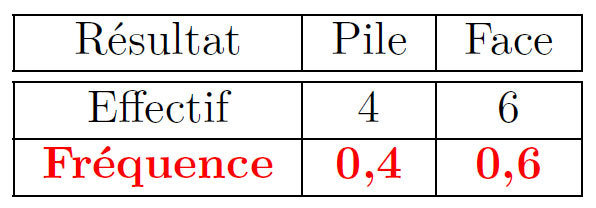
Exemple : On lance dix fois de suite une pièce bien équilibrée.
On obtient P (Pile), F (Face), F, F, P, P, F, P,F, F.
- Il s’agit d’un échantillon de taille 10 (on a répété l’expérience 10 fois).
- La distribution des fréquences est :
Remarques :
- Les distributions de fréquences varient d’un échantillon à l’autre pour la même expérience. C’est ce qu’on appelle la fluctuation d’échantillonnage.
- Même pour des échantillon de même taille, la distribution de fréquences peut varier.
- Lorsque la taille de l’échantillon augmente, les distributions de fréquences ont tendance à se stabiliser.
Plus précisément, on a la propriété suivante, vue en classe de Seconde :
Propriété : (admise)
Soit un caractère dont la proportion dans une population donnée est p.
alors 95 % des échantillons de taille n auront une distribution de fréquences dans laquelle la fréquence du caractère sera dans l’intervalle :
Cet intervalle est appelé intervalle de fluctuation au seuil de 95 %.
4.2 Intervalle de fluctuation à 95 % selon la loi binomiale
Définition :
Soit un caractère dont la proportion dans une population donnée est p.
L’intervalle de fluctuation à 95 % d’une fréquence, pour un échantillon de taille n, selon la loi binomiale de paramètres n et p est :
avec
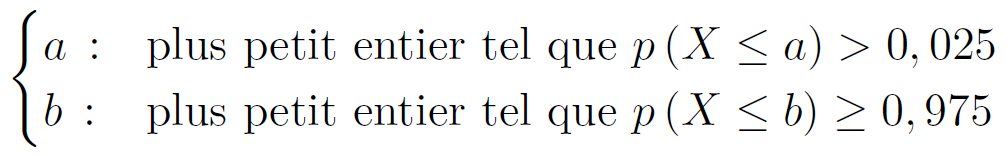
Remarque :
On admettra que si , cet intervalle de fluctuation est sensiblement le même que celui étudié en seconde.
4.3 Prise de décision à partir d’un échantillon
On considère une population dans laquelle on suppose que la proportion d’un caractère est p.
On observe la fréquence f de ce caractère dans un échantillon de taille n et on considère l’hypothèse « la proportion de ce caractère dans la population est p ».
On a alors la règle de décision suivante :
on considère que l’hypothèse n’est pas remise en question et on l'accepte au seuil de risque de 5 % ;
on rejette l’hypothèse au seuil de risque de 5 %.

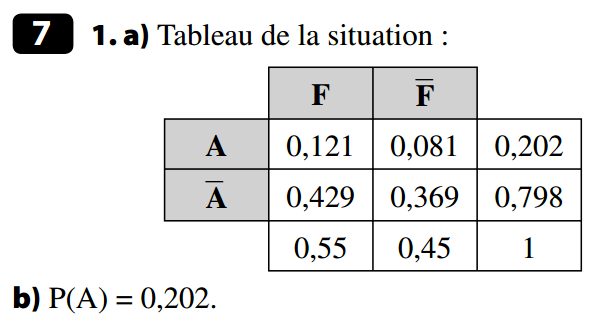
Les contrôles des 256 automobilistes se font de façon identique et indépendante. La probabilité qu'un automobiliste soit en infraction est égale à 0,5. Le contrôle de police est donc un schéma de Bernoulli de paramètres n = 256 et p = 0,5. Ainsi I suit la loi binomiale B(256 ; 0,5).
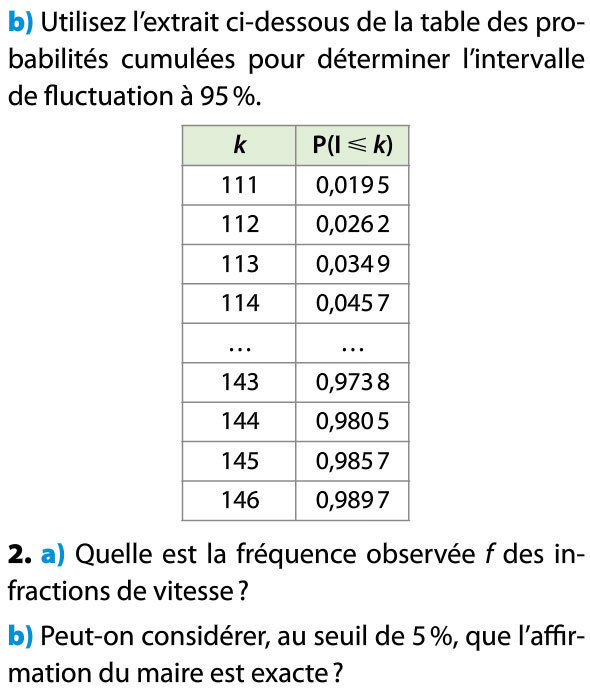
donc on peut considérer, au seuil de 5% (c'est à dire avec un risque de 5% de se tromper) que l'affirmation du maire est exacte.

a) Les contrôles des 200 bouteilles se font de façon identique et indépendante. La probabilité qu'une bouteille soit défectueuse est égale à 0,05. Le contrôle de la production est donc un schéma de Bernoulli de paramètres n = 200 et p = 0,05. Ainsi X la variable aléatoire qui donne le nombre de bouteilles défectueuses suit la loi binomiale B(200 ; 0,05).
b)
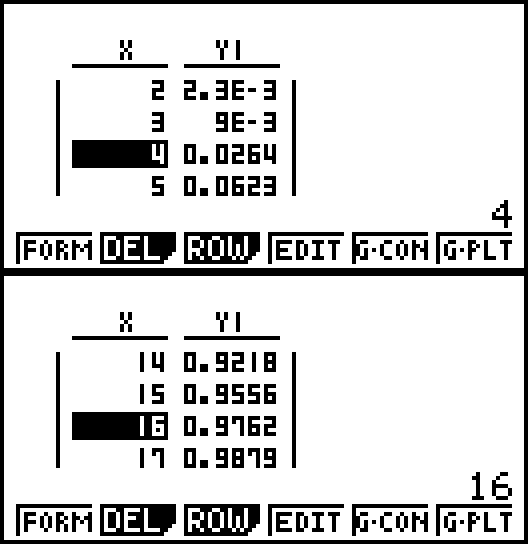

donc on peut considérer, au seuil de 5%, que la chaîne ne fonctionne pas correctement.
C'est la probabilité que X prenne une valeur dans la zone de rejet. Ainsi il y une probabilité d'environ 3,3% de rejeter l'hypothèse
"la chaîne fonctionne correctement" alors qu'elle est vraie.

a) Les contrôles des 428 modems se font de façon identique et indépendante. La probabilité qu'un modem soit défectueux est égale à 0,16. L'enquête est donc un schéma de Bernoulli de paramètres n = 428 et p = 0,16. Ainsi Y la variable aléatoire qui correspond au nombre de modems défectueux suit la loi binomiale B(428 ; 0,16).
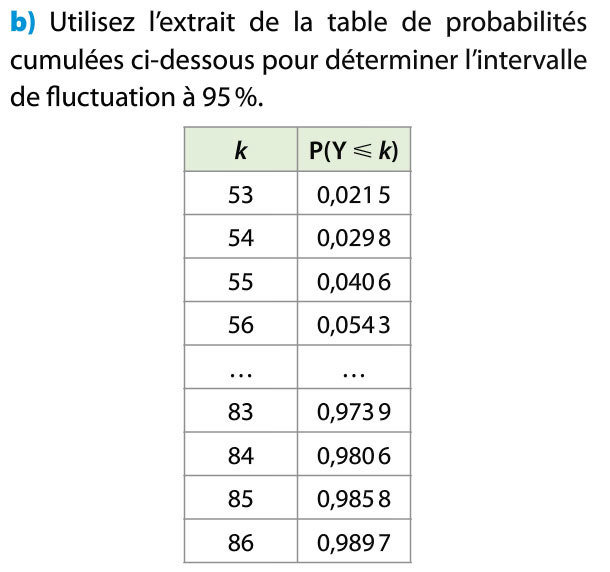

On rejette, au seuil de 5%, l’hypothèse p = 0,16. L’association de consommateurs infirme les indications du fournisseur d’accès.
c) Il s’agit de déterminer la probabilité que la fréquence soit dans la zone de rejet.
Il y a environ 4% de chance de commettre une erreur lors de la prise de décision.
1S : Loi Binomiale
By Jean-Marc Kraëber
1S : Loi Binomiale
Lycée Saint-Exupery
- 4,295



