RoundingSat

recent work on
pseudo-Boolean solving

Jo Devriendt †, Jan Elffers †, Ambros Gleixner ‡, Jakob Nordström *
† KTH Royal Institute of Technology, Sweden

‡ Zuse Institut Berlin, Germany

* University of Copenhagen, Denmark

jhmde@kth.se

  1. PB solvers & learning
  2. Leveraging LP solving for PB solving

Talk in two parts

Pseudo-Boolean background

  • Pseudo-Boolean (PB) constraint:
    • Bounded weighted sum of literals:

       
    • Note:
    • Equivalent to 0-1 integer linear programming constraint
  • PB formula: conjunction of PB constraints
  • PB solvers decide satisfiability of PB formula
  • PB generalizes SAT
x \vee \neg y \vee z \Leftrightarrow x+\overline{y}+z \geq 1
x+2\overline{y}+3z+4\overline{w} \geq 5
\overline{x} = 1-x
  • State-of-the-art PB systems:
    MiniSat+, Sat4J, Open-WBO, NaPS, RoundingSat
    • Most translate to SAT
  • MIP systems also have strong (Optimization) PB performance

Why pseudo-Boolean?

Strong learning!

  • Conflict-Driven Conflict Learning (CDCL) SAT solvers learn implied clause from each conflict
    • Study of resolution proof system characterizes SAT solver performance
  • RoundingSat (and Sat4J) learn implied PB constraint from each conflict
    • Study of cutting plane (CP) proof system characterizes RoundingSat performance
  • CP polynomially simulates resolution
    • PB solvers can be exponentially stronger than SAT solvers on same instance

On learning

What is a proof system?

  • Language to write statements
  • Syntactical inference rules

Informally

  • Propositional clauses

     
  • Resolution rule
\frac{C \vee p \;\;\;\; D \vee \neg p}{C \vee D}
C \equiv a \vee \neg b \vee c

Resolution proof system

Resolution proof system

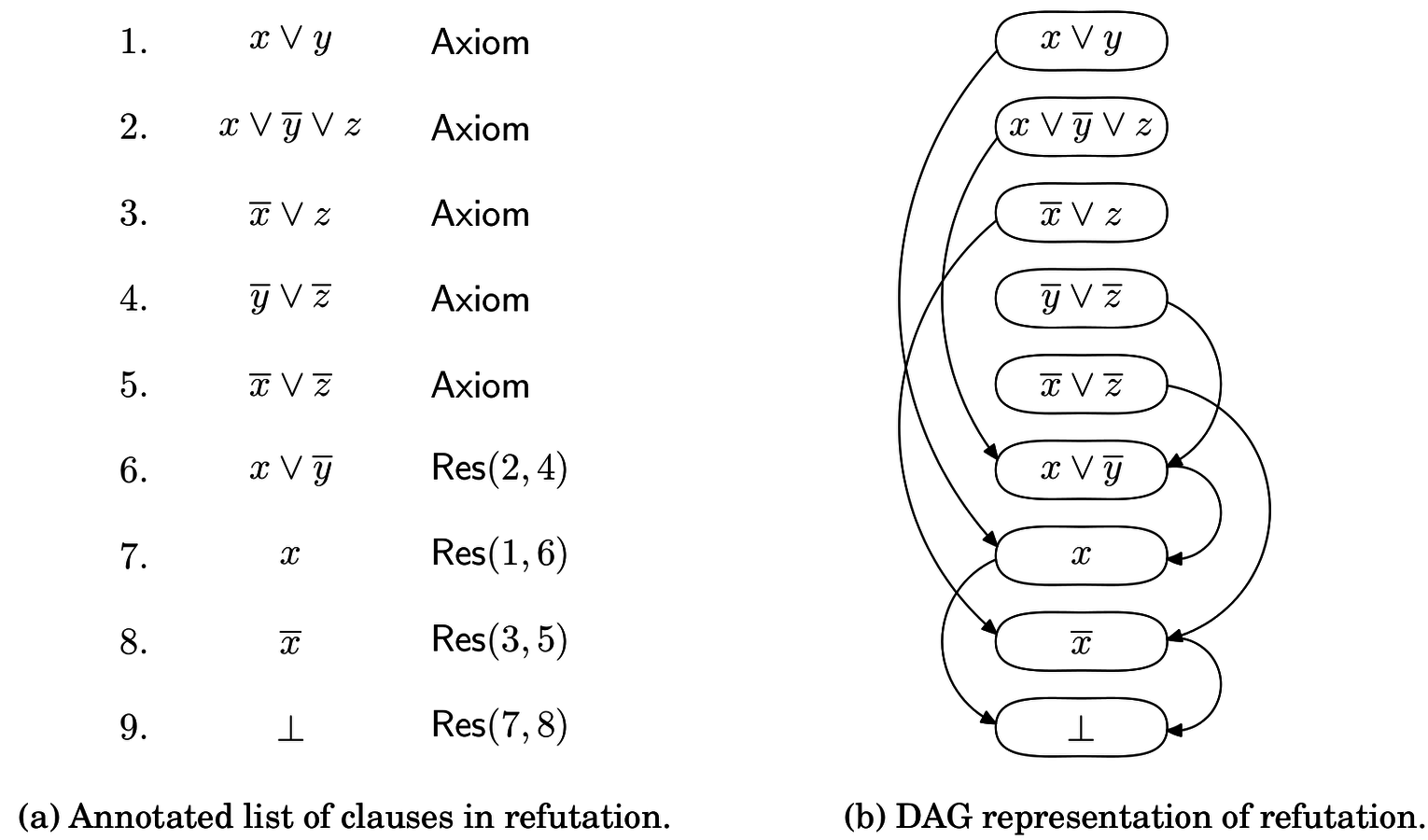
Cutting plane proof system

  • Linear inequalities:

     
  • Inference rules:
a_1x_1+a_2x_2+a_3x_3 \geq A \;\;\;\; a_i,A \in \mathbb{Z}, x_i \mapsto \mathbb{Z}

Cutting plane proof system

  1.     -2x +    y ≥ 0     (axiom)
  2.        x + -2y ≥ -2    (axiom)
  3.      2x +    y ≥ 2      (axiom)
  4.      2x + -4y ≥ -4    (2*2)
  5.              -3y ≥ -4    (1+4)
  6.                -y ≥ -1    (rounding of 5)
  7.      2x          ≥ 1     (3+6)
  8.        x          ≥ 1     (rounding of 7)
  9.     -2x          ≥ -1    (1+6)
  10.       -x          ≥ 0     (rounding of 9)
  11.                 0 ≥ 1     (8+10)
\forall x\colon \#\{y~|~InHole(x,y) \} \geq 1 \\ \forall y\colon \#\{x~|~InHole(x,y) \} \leq 1
  • E.g., consider:



     
    • Cardinality constraints
    • MX is UNSAT if domain of x > domain of y
  • IDP* will timeout for domain size > 20
    • IDP uses clausal learning (resolution)
  • RoundingSat will find solution easily
    • RoundingSat uses PB learning (cutting planes)
  • *Symmetry is not always the answer

On learning

On learning

  • CP > resolution, so RoundingSat > IDP?
    • RoundingSat does canceling addition CP
      • On CNF inputs, equivalent to resolution
    • Existence of a short proof does not imply efficient deduction of a short proof
      • E.g., for rationally infeasible instances
  • Only two practical "CDCL" proof systems
    • resolution
    • canceling addition CP for PB
  • Not obvious to generalize to integer setting
    • see IntSat work

currently, PB solvers learn best

RoundingSat's idea

  • From every conflict, generate PB constraint
  • Obvious idea: canceling addition instead of resolving
x+2y+2z \geq 3 \\ -3z+2w+v \geq 0 \\ \models \\ 3x+6y+4w+2v \geq 9
\text{decisions: }\{\overline{x},\overline{v}\}
  • Problem: does not preserve falsification
  • Solution: divide and round reason constraint to be "tight"
x+y+z \geq 2 \\ -3z+2w+v \geq 0 \\ \models \\ 3x+3y+2w+v \geq 6

Rational infeasibility

  • PB formula can be rationally infeasible
    • no assignment to interval [0,1] satisfies the formula, e.g.:


       
  • Rational infeasibility implies UNSAT
  • CNF formula is rationally infeasible
    • iff unit propagation leads to conflict
  • Otherwise, trivial rational solution: assign 0.5 to all non-propagated variables
    • All clauses not satisfied by unit propagation have at least 2 unassigned literals
    • Such clauses are satisfied by 0.5-assignment
x+y+z \geq 2 \\ \overline{x}+\overline{y}+\overline{z} \geq 2

For CNF, deciding rational infeasibility is trivial

  • Deciding rational infeasibility of PB formulas is easy in theory:
    • Algorithmic complexity class: P [K1979]
    • Proof-theoretic complexity: short CP [CCT87] proofs exist [F1902]
  • Linear programming (LP) solvers efficiently decide rational feasibility
  • In practice, many PB solvers struggle on rationally infeasible formulas [EGNV18]
    • Even PB solvers that natively build cutting plane proofs, e.g.,  RoundingSat and Sat4J

Goal of our work:
use LP solver to check rational feasibility during PB search

Rational infeasibility

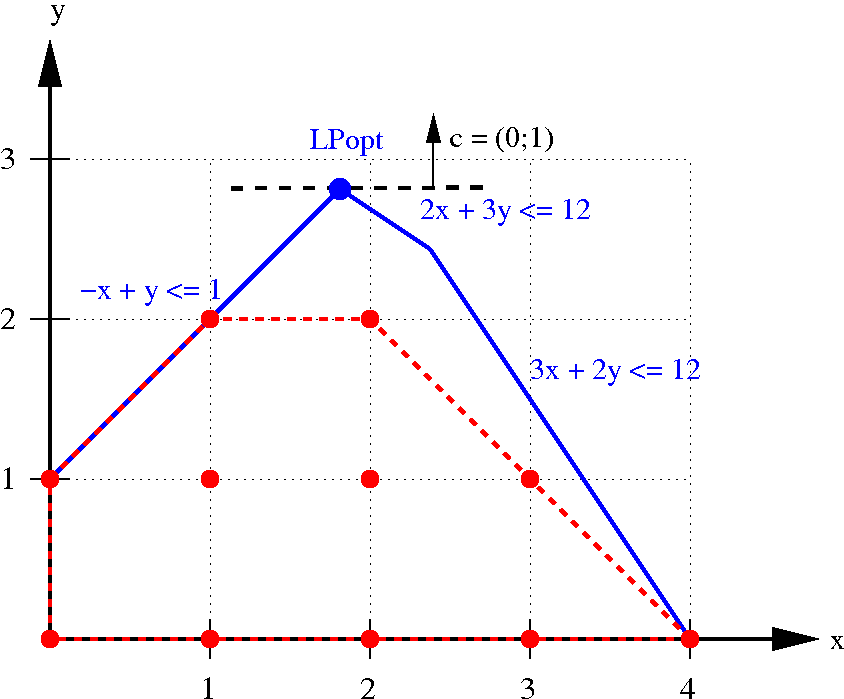
Linear Programming (LP) solver

  • Input:
    • conjunction of linear constraints
    • variable bounds
    • objective function
  • Output: either
    • SAT: optimal rational solution
    • UNSAT: Farkas multipliers
      • defines violated positive linear combination of input constraints

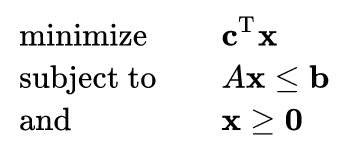
PB search loop

Propagation

Conflict?

Learn PB constraint

Backjump

Decide unassigned variable

yes

no

PB search loop

with LP solver call

Propagation

Conflict?

Backjump

Decide unassigned variable

no

Rational infeasibility?

Query LP solver

yes

no

Learn PB constraint

Extract Farkas multipliers

yes

Learn Farkas constraint

  • LP solvers are slow compared to PB search loop
    • Limit calls to LP solver
    • Limit LP solver running time
    • Deterministic measure: compare #conflicts in PB solver to #pivots in LP solver
  • Learned constraint must be implied by input formula
    • LP solver uses inexact floating point arithmetic
    • Recalculate Farkas constraint with exact arithmetic
    • Verify Farkas constraint is still conflicting

Two technical hurdles

  • PB solver RoundingSat [EN18]
    • Native cutting plane proofs
    • Performed well in past PB competitions
  • LP solver SoPlex [ZIB]
    • SCIP's native LP solver
    • Fast
    • Open source

Working implementation

Experiments!

  • 5 solver configurations
    • RoundingSat
    • RoundingSat+SoPlex
    • SCIP
    • Sat4J
    • Sat4J-CP
  • 3000s on 16GiB machines
  • 4 benchmark families:
    • PB12
    • PB16
    • MIPLIB
    • PROOF

Performance experiment

Performance experiment

Performance experiment

Performance experiment

  • RoundingSat+SoPlex never really worse than RoundingSat
    • small LP overhead at worst, huge speedups at best
    • Not only more solved UNSAT instances (+16%), but also more solved SAT instances (+14%)
  • RoundingSat+SoPlex and SCIP trade places
  • SoPlex does not like PB12

Performance experiment

Conflict depth experiment

Conflict depth experiment

  • Conflict depth for rational infeasibility check and unit propagation are similar
  • Technique detects rational infeasibility also in deep search nodes

Learned constraint addition experiment

Learned constraint addition experiment

  • Adding learned constraints to LP solver does not lead to more solved instances
    • Also no improvement in number of conflicts needed
  • Hypothesis 1: no objective function to guide "tight" variant
  • Hypothesis 2: rational solution at deep search nodes is not useful
  • Other hypotheses?

Current work

  • Optimization
  • LP cut generation

[K1979] A polynomial algorithm for linear programming - 1979 - Khachiyan

[CCT87] On the Complexity of Cutting-Plane Proofs - Cook, Coullard, Turán

[F1902]  Über die Theorie der Einfachen Ungleichungen - 1902 - Farkas

[EGNV18] Using combinatorial benchmarks to probe the reasoning power of pseudo-Boolean solvers - 2018 - Elffers, Giráldez-Cru, Nordström, Vinyals

[EN18] Divide and conquer: Towards faster pseudo-boolean solving - 2018 - Elffers, Nordström

[ZIB] SoPlex - soplex.zib.de

References

How about rational variables?

  • Mixed Integer Programming (MIP)
    • constraints have both discrete and continuous variables
  • Integrate in CDCL-like system throught SMT-style theory reasoning
  • Potential advanced approach:
    1. split theory in integral         and continuous      
      s.t.
    2. decide
    3. call rational system to extend         to                       or learn falsified constraint. E.g. (exact) LP solver
  • Note: for model counting or deduction,         is representative of model class containing
T_\mathbb{Z}
T_\mathbb{Q}
T_\mathbb{Q} \models T_\mathbb{Z}
M_\mathbb{Z}
M_\mathbb{Z} \models T_\mathbb{Z}
M_\mathbb{Q} \models T_\mathbb{Q}
M_\mathbb{Z}
M_\mathbb{Q}

RoundingSat 2019: recent work on PB solving

By Jo Devriendt

RoundingSat 2019: recent work on PB solving

  • 974

More from Jo Devriendt