Collective Cell Migration &

Cell-Cell Communication

 

Julien Varennes and Prof. Andrew Mugler

Collective Cell Migration

  • A variety of different cells use inter-cellular communication in order to coordinate behavior.
  • Groups of cells may use inter-cellular communication in order to better sense their environment.
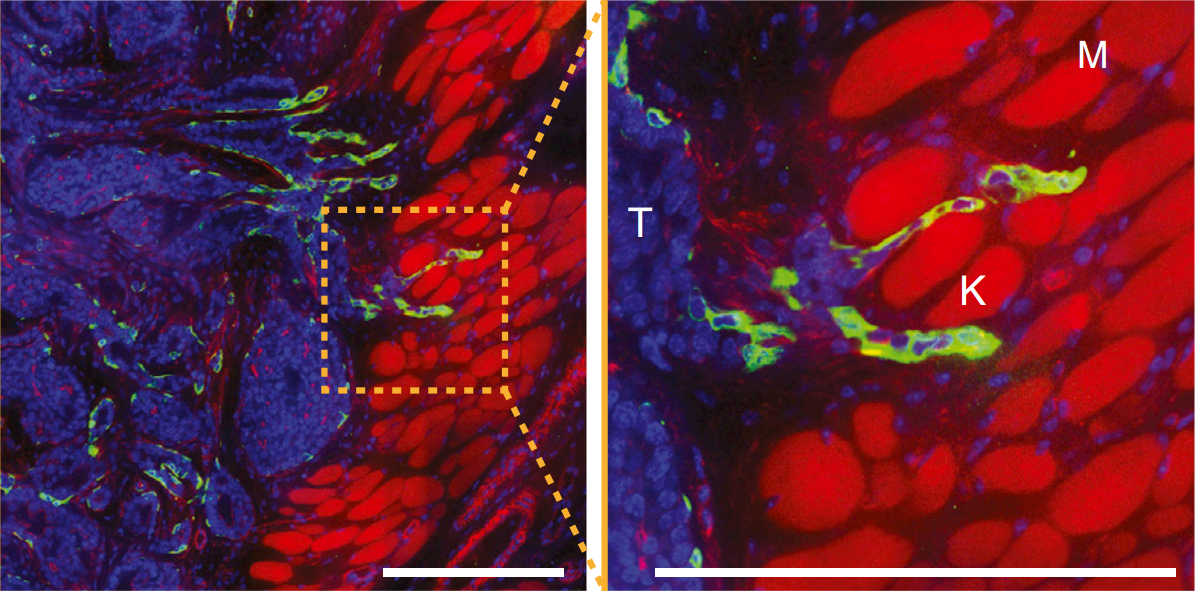
  • Tumors exploit this trait during the invasion of tumor cells into the surrounding tissue.
200 \mu m
200μm200 \mu m

Tumor

Collective Cell Migration

  • In the case of breast cancer, it has been observed that invasion occurs in the form of cell clusters.
  • Recently, it has been shown that multicellular clusters can sense their environment with a higher precision than single cells.

Is there an optimal group size for most efficient collective cell migration? 

Model Basics

  • Cells migrate in groups.
    • Cell's interact with their surroundings via adhesive energies.
      • Cell-cell adhesion
      • Cell-ECM adhesion

Model Basics

  • Cells have a desired (resting) size
  • Cell movement may be biased via cell polarization.
    • Each cell has a polarization vector.

Cell-Cell Communication Model

  • We use a minimal adaptive model based on local excitation and global inhibition (LEGI).
    • S is the signaling molecule
    • X is the local reporter, Y is the global reporter
    • R is the downstream read-out
S \rightarrow S+X+Y
S→S+X+YS \rightarrow S+X+Y
X \rightarrow R
X→RX \rightarrow R
Y \dashv R
Y⊣RY \dashv R

Cell-Cell Communication Model

Reactions in each cell

s_k \rightarrow s_k + x_k: \ \kappa
sk→sk+xk: κs_k \rightarrow s_k + x_k: \ \kappa
s_k \rightarrow s_k + y_k: \ \kappa
sk→sk+yk: κs_k \rightarrow s_k + y_k: \ \kappa
x_k \rightarrow \emptyset: \ \mu
xk→∅: μx_k \rightarrow \emptyset: \ \mu
y_k \rightarrow \emptyset: \ \mu
yk→∅: μy_k \rightarrow \emptyset: \ \mu
y_k \rightleftharpoons y_{k\pm1}: \ \gamma_{k,k\pm1}
yk⇌yk±1: γk,k±1y_k \rightleftharpoons y_{k\pm1}: \ \gamma_{k,k\pm1}
R_k = x_k - y_k
Rk=xk−ykR_k = x_k - y_k
S \rightarrow S+X+Y
S→S+X+YS \rightarrow S+X+Y
X \rightarrow R
X→RX \rightarrow R
Y \dashv R
Y⊣RY \dashv R

How does communication influence cell migration?

  • We assume that cells that are in contact are repelled from one another.
    • This affects the dynamics via the cell's polarization.
\vec{p}_k \equiv \text{cell polarization,} \ \ \vec{q}_k \equiv \text{cell repulsion}
p⃗k≡cell polarization,  q⃗k≡cell repulsion\vec{p}_k \equiv \text{cell polarization,} \ \ \vec{q}_k \equiv \text{cell repulsion}
\frac{d\vec{p}_k}{dt} = -\frac{1}{\tau} \vec{p}_k + \epsilon R_k \ \vec{q}_k
dp⃗kdt=−1τp⃗k+ϵRk q⃗k\frac{d\vec{p}_k}{dt} = -\frac{1}{\tau} \vec{p}_k + \epsilon R_k \ \vec{q}_k

polarization

repulsion

Implementation: Cellular Potts Model

Cell behavior is simulated using CPM.

u = \sum_{i,j} J_{i,j} + \lambda \sum_{i=1}^N (V_T-V_i)^2
u=∑i,jJi,j+λ∑i=1N(VT−Vi)2u = \sum_{i,j} J_{i,j} + \lambda \sum_{i=1}^N (V_T-V_i)^2
\alpha
α\alpha
\beta
β\beta
\sigma_i \in 1, 2, 3, ...
σi∈1,2,3,...\sigma_i \in 1, 2, 3, ...
\sigma_i = 0
σi=0\sigma_i = 0

For individual cells:

For ECM:

Implementation: Cellular Potts Model

A change in the spin value of a pixel is accpeted with the following probabiliy.

w = \sum_{k = \sigma_a, \sigma_b} \frac{\Delta\vec{x}_{k(a \to b)} \cdot \vec{p}_k}{ |\Delta\vec{x}_{k(a \to b)}|}
w=∑k=σa,σbΔx⃗k(a→b)⋅p⃗k∣Δx⃗k(a→b)∣w = \sum_{k = \sigma_a, \sigma_b} \frac{\Delta\vec{x}_{k(a \to b)} \cdot \vec{p}_k}{ |\Delta\vec{x}_{k(a \to b)}|}
u = \sum_{i,j} J_{i,j} + \lambda \sum_{i=1}^N (V_T-V_i)^2
u=∑i,jJi,j+λ∑i=1N(VT−Vi)2u = \sum_{i,j} J_{i,j} + \lambda \sum_{i=1}^N (V_T-V_i)^2

Chemical Concentration

Collective Cell Migration

By Julien Varennes

Made with Slides.com

Collective Cell Migration

  • 1,578

More from Julien Varennes