An initial investigation of the performance of GPU-based swept time-space decomposition

Daniel Magee

Kyle E. Niemeyer

 

School of Mechanical, Industrial, & Manufacturing Engineering

Oregon State University

 

January 11 - AIAA SciTech 2017 - Grapevine, TX

Why ?

https://www.nasa.gov/mission_pages/juno/launch/#.WHVhIhvQfIU

https://www.youtube.com/watch?v=Ti5zUD08w5s

http://www.wikiwand.com/ro/Airbus_Beluga

Why GPU?

Heterogeneous clusters are becoming more common

GPGPUs offer significant parallelism in a workstation

https://www.olcf.ornl.gov/2013/06/12/titan-completes-acceptance-testing/

Heat Equation

\frac{\partial T}{\partial t} = \alpha \nabla^2 T \;
∂T∂t=α∇2T\frac{\partial T}{\partial t} = \alpha \nabla^2 T \;
T_i^{m+1} = \text{Fo} (T_{i+1}^m + T_{i-1}^m) + (1-2 \text{Fo}) T_i^m \;
Tim+1=Fo(Ti+1m+Ti−1m)+(1−2Fo)TimT_i^{m+1} = \text{Fo} (T_{i+1}^m + T_{i-1}^m) + (1-2 \text{Fo}) T_i^m \;

Important aspects:

  • First order in time
  • Three-point stencil
  • Insulated boundary conditions

Test cases

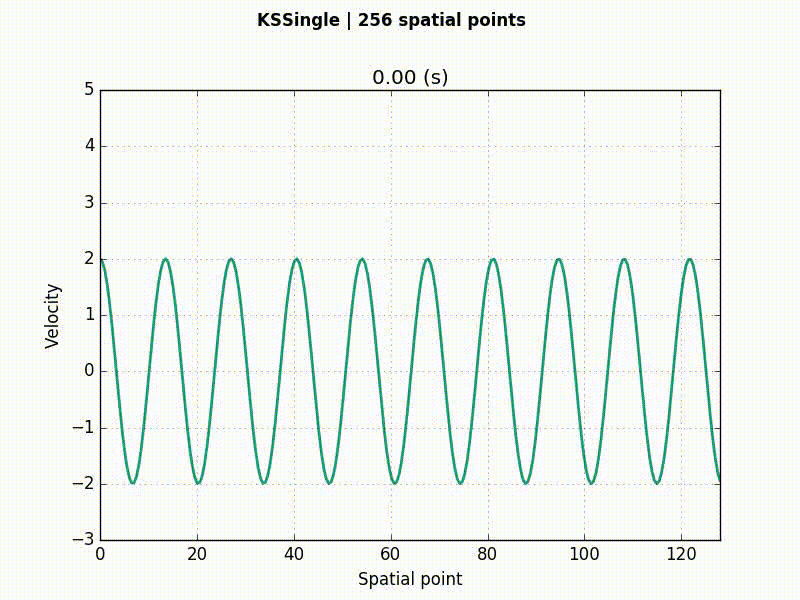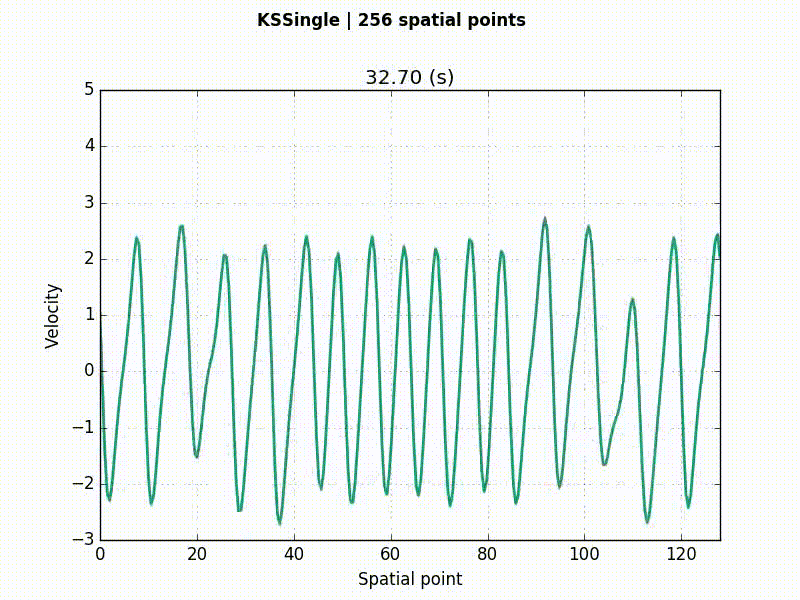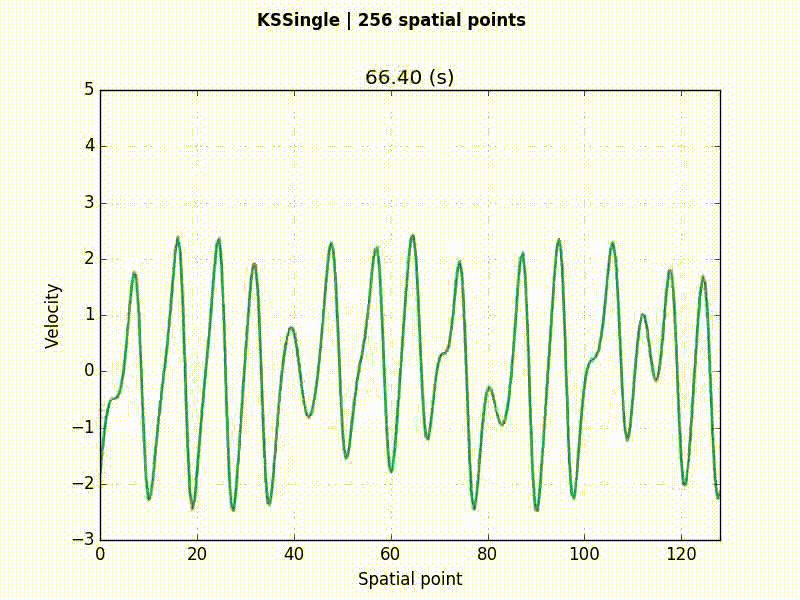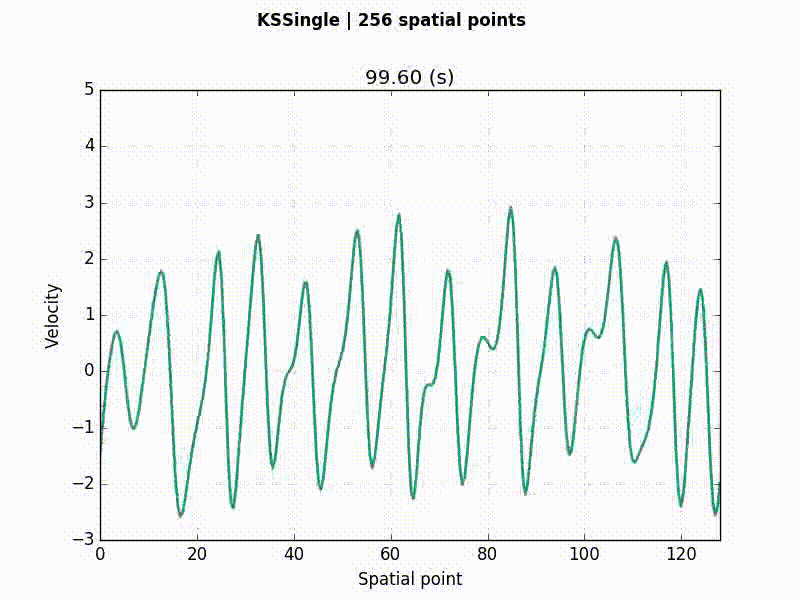
Kuramoto–Sivashinsky (KS) equation

u_t = -(uu_x + u_{xx} + u_{xxxx}) = -\left( \frac{1}{2} u_x^2 + u_{xx} + u_{xxxx} \right) \;
ut=−(uux+uxx+uxxxx)=−(12ux2+uxx+uxxxx)u_t = -(uu_x + u_{xx} + u_{xxxx}) = -\left( \frac{1}{2} u_x^2 + u_{xx} + u_{xxxx} \right) \;
\frac{u_i^{m+1}-u_i^m}{\Delta t} = -\left( \frac{(u_{i+1}^m)^2 - (u_{i-1}^m)^2}{4\Delta x} + \frac{u_{i+1}^m + u_{i-1}^m + 2u_i^m}{\Delta x^2} + \frac{u_{i+2}^m - 4u_{i+1}^m + 6u_i^m - 4u_{i-1}^m + u_{i-2}^m}{\Delta x^4} \right) \;
uim+1−uimΔt=−((ui+1m)2−(ui−1m)24Δx+ui+1m+ui−1m+2uimΔx2+ui+2m−4ui+1m+6uim−4ui−1m+ui−2mΔx4)\frac{u_i^{m+1}-u_i^m}{\Delta t} = -\left( \frac{(u_{i+1}^m)^2 - (u_{i-1}^m)^2}{4\Delta x} + \frac{u_{i+1}^m + u_{i-1}^m + 2u_i^m}{\Delta x^2} + \frac{u_{i+2}^m - 4u_{i+1}^m + 6u_i^m - 4u_{i-1}^m + u_{i-2}^m}{\Delta x^4} \right) \;

Important aspects:

  • Second order in time (RK2)
  • Five-point stencil
  • Periodic boundary conditions.

Overview

  • The swept rule as a response to barriers in parallel programming.
  • GPU architecture
  • Swept schemes on GPU
  • Performance results
  • Swept Rule introduced by Alhubail and Wang

"The swept rule for breaking the latency barrier in time advancing PDEs", Journal of Computational Physics, 2015

The problem:

t

x

How to effectively decompose the space-time domain for parallel processing?

"Shared" memory systems

t

x

Distributed memory systems

t

x

Ghost Region

Latency Bandwidth
Analogy Fixed cost Variable cost
Best Case 700 ns ~ .1 ns per double

The cost of distributed communication

Node

0

Node

1

"The swept rule for breaking the latency barrier in time advancing PDEs", Journal of Computational Physics, 2015

Do as much work as possible on the data in the fastest memory before writing to the slowest memory.

t

x

General Principle

A very brief introduction to the GPU

Block

Streaming Multiprocessor (SM)

Warp

Thread

Physical

Abstract

32 threads

Memory hierarchy

Global

Shared

Register

All threads 

Block

Warp

Accessible to

Lifetime

Application

Kernel

Kernel

Slowest

Fastest

Heat example

Advance n (node length) timesteps with 2 communications

Swept Rule Procedure

Triangle storage dilemma

(n/2+1) \times n/2 \times \text{size}
(n/2+1)×n/2×size(n/2+1) \times n/2 \times \text{size}

To save every point requires:

129 \times 128 \times 8 = 132 \text{kB}
129×128×8=132kB129 \times 128 \times 8 = 132 \text{kB}

If n=256 at double precision

t

x

t

x

Data folding solution

Now a triangle with base 256 can be stored in two rows of 256.

256 \times 2 \times 8 = 4 \text{kB}
256×2×8=4kB256 \times 2 \times 8 = 4 \text{kB}

Extended stencil & second order

  • Higher order derivatives require larger stencils in time or space
  • Fourth derivative requires either a five-point stencil or an intermediate flux computation

This value is required for 

this calculation

KS example

Solution

Extend stencil in space not time.

 

Flatter triangle with no intermediate spatial steps is able to be folded as in previous example.

SharedGPU:

  • Used for Heat and KS
  • Node -> Block
  • Shared memory working array

Organizing the Swept Rule

Hybrid:

  • Heat only
  • Passes split node to CPU 

Register:

  • KS only
  • Node -> Warp
  • Registers for working array

A note on "Classic" version


__global__ void classicKS(const REAL *ks_in, REAL *ks_out, bool finally)
{
    int gid = blockDim.x * blockIdx.x + threadIdx.x; //Global Thread ID
    int lastidx = ((blockDim.x*gridDim.x)-1); 
    int gidz[5];

    #pragma unroll
    //indices of previous values
    for (int k=-2; k<3; k++) gidz[k+2] = (gid+k) & lastidx; 

    if (finally) 
    {
	ks_out[gid] += finalStep(ks_in, gidz);
    }
    else 
    {
	ks_out[gid] = predictorStep(ks_in, gidz);
    }
}

  • Problem sizes 2048–1,048,576 by powers of 2

  • Block sizes 32–1024 by powers of 2

  • Double precision

  • Results are the best block size for each scenario.

Testing:

Results

GPU: Nvidia Tesla K40c

745 MHz | 15 SM

CPU: Intel Xeon 2630-E5

2.4 GHz | 8 cores | 16 threads

Equipment:

Heat

K–S

Parallel CPU with MPI vs GPU

K–S equation

"The swept rule for breaking the latency barrier in time advancing PDEs", Journal of Computational Physics, 2015

MPI program from Alhubail and Wang:

Conclusions

  • The swept rule improves on the classic finite difference decomposition by 6x for smaller problem sizes and 2x for larger problem sizes for both test cases.
  • Using only the GPU and storing the working array in shared memory was the most effective swept rule version.
  • Parallel finite difference codes on workstations can be sped up by several orders of magnitude using even naive GPU kernels.

Future work

  • Applying this work to heterogeneous cluster architecture using CUDA aware MPI.
  • Explore the effect of block-size on performance. 
  • Extend to 2-D.

Acknowledgements

Questions?

code available at

github.com/Niemeyer-Research-Group/1DsweptCUDA

SciTech Prez

By mageed

Made with Slides.com

SciTech Prez

Presentation for AIAA SciTech conference January 2017 in Grapevine, Texas.

  • 1,400