Subset Sum

by Mithun Selvaratnam

Given a target sum and an array of positive integers, return true if any combination of numbers in the array can add to the target.

 Each number in the array may only be used once. Return false if the numbers cannot be used to add to the target sum.

Question

Examples

subsetSum(9, [1,10,5,3]); // true, 1 + 5 + 3
subsetSum(19, [1,10,5,3]); // true, add all 4
subsetSum(17, [1,10,5,3]); // false

subsetSum(2, [1,10,5,3]); // false
subsetSum(10, [1,10,5,3]); // true, since 10 + 0 = 10

Iterative Solution

Construct an array of all possible sums:

• initialize sum array with 0 // [0]
• iterate through input array
• iterate through sum array, checking if current element + sum equals our target
• if the new sum is less than the target, store it in the sum array

example: subsetSum(17, [1, 10, 5, 3])

=> set of possible sums: [0]

=> add 1 to each possible sum

=> set of possible sums: [0, 1]

=> add 10 to each possible sum

=> set of possible sums: [0, 1, 10, 11]

=> add 5 to each possible sum

=> set of possible sums: [0, 1, 10, 11, 5, 6, 15, 16]

Code

function subsetSum(target, arr){
  let sums = [0];
  for (let i = 0; i < arr.length; i++){
    let sumsCopy = [...sums]; // create a new array to iterate through; 
                              // iterating through the array that we're 
                              // mutating will lead to some weird behavior
    for (let j = 0; j < sumsCopy.length; j++){
      let newSum = sumsCopy[j] + arr[i];
      if (newSum === target) return true;
      else if (newSum < target) sums.push(newSum);
    }
  }
  return false;
}

Time complexity: 2^n 

The sums array grows by a factor of 2 for each step

The last arr element has to iterate through 2^(n-1) sums

Recursive Solution

We can also approach this problem recursively.

For each element of the array, we are only concerned with whether

(1) using it to construct a sum will reach the target

(2) skipping it and adding a different set of numbers will reach the target

So for each element, let's make a recursive call that checks those two things.

k dude but how??

1) To include the element in our potential sum, subtract the element from the target

2) To skip the number, keep the target the same, but still increment the index

const whenExcluded = subsetSum(target, nums, idx + 1);

const whenIncluded = subsetSum(target - num, nums, idx + 1);

// return whether either possibility came back true
return whenExcluded || whenIncluded;

Code

// initialize the index to 0
function subsetSum (target, nums, idx = 0) {
  // if we've hit 0 we're done!
  if (target === 0) return true;
  // stop trying and return false if the target is negative OR 
  // if we've reached the end of the array
  if (target < 0 || idx === nums.length) return false;
  const num = nums[idx];
  // capture the boolean result for the possibility of *excluding* 
  // the current number from the sum
  // recursively try with the same target, but continue onto the next index
  const whenExcluded = subsetSum(target, nums, idx + 1);
  // capture the boolean result for the possibility of *including* 
  // the current number in the sum
  // recursively try with the target minus this number and continue onto the next index
  const whenIncluded = subsetSum(target - num, nums, idx + 1);
  // return whether either possibility came back true
  return whenExcluded || whenIncluded;
}

Each target passed to 'whenIncluded' can be thought of as a subtarget

Visualization

This function makes two calls each time the recursive case executes (like recursive factorial) - a tree is the best way to visualize it

Time complexity: O(2^n)  :(

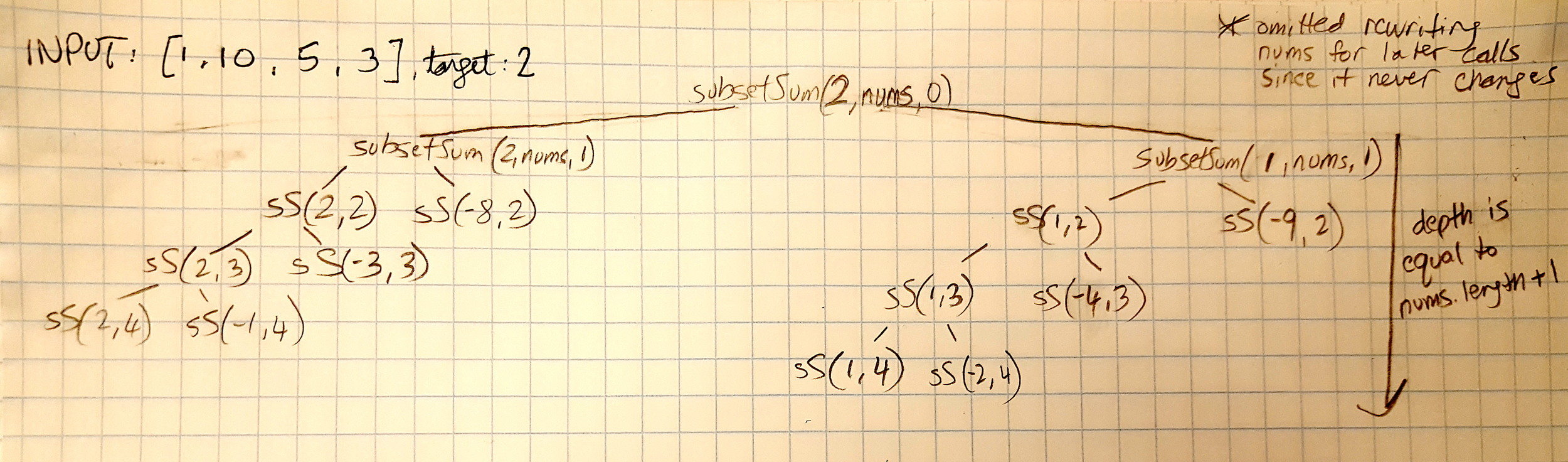
Optimize

Consider the following input array:

[1, 10, 5, 3, 2, 4]

There are multiple ways to reach the partial sum of 5 by adding these numbers (5 + 0, 3 + 2, 4 + 1)

Our recursive function will process all the recursive calls for the subtarget n - 5 EVERY time it runs into these combinations, even though the result will always be the same

Memoize it!

With a little memoization, we can cut down on that extra work, by storing the results of each subtarget

function subsetSum (target, nums, idx = 0, memo = {}) {
  // if we've seen this target and already solved for it, return the answer right away
  if (memo.hasOwnProperty(target)) return memo[target];

  if (target === 0) return true;

  if (target < 0 || idx === nums.length) return false;
  const num = nums[idx];
  const whenExcluded = subsetSum(target, nums, idx + 1, memo);
  const whenIncluded = subsetSum(target - num, nums, idx + 1, memo);

  // determine whether either possibility came back true
  const result = whenExcluded || whenIncluded;
  // cache this answer, associating it with this particular target
  memo[target] = result;
  return result;
}

Time complexity: still 2^n, but better than before

Worst case: target unreachable and no repeated operations