Designing Design Systems
by Oleg Nizhnikov from Evolution gaming
Designing Design Systems
A gentle intro to applied category theory
by Oleg Nizhnikov from Evolution gaming
Designing Design Systems
A gentle intro to applied category theory
for tired developers
by Oleg Nizhnikov from Evolution gaming
Change of perspective
Boxes and Arrows
System Design
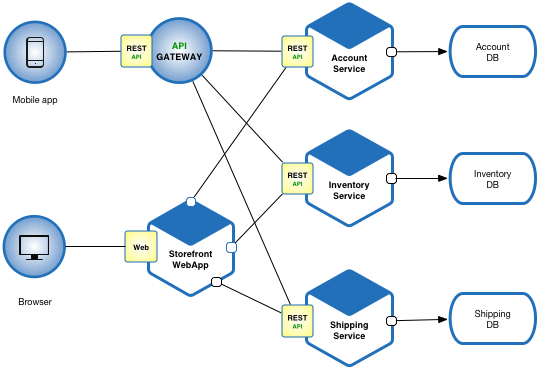
taken from microservices.io/patterns/microservices
Modules
Business processes
Industry
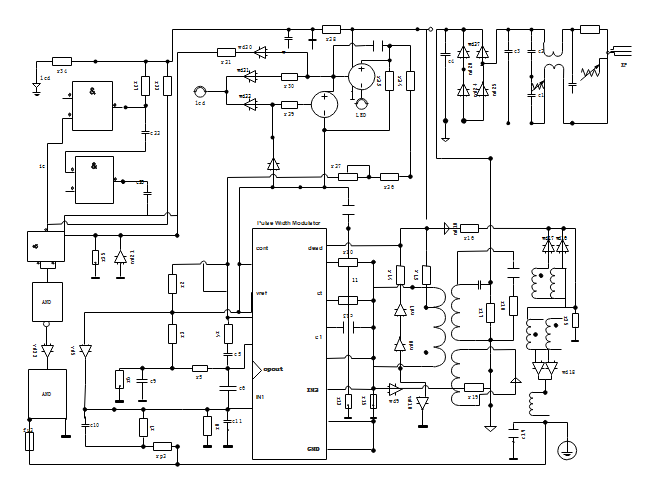
Electical circuits
Monoidal Category
Box
Box
Input
Output
Morphism
Domain
Codomain
Category
Box
Input
Output
Monoidal Category
Box A
Input A
Output A
Horizontal Composition
Box B
Output B
Input B
Box A
Input A
Horizontal Composition
Box B
Output B
Wiring
Box B•A
Box A
Input A
Output A
Vertical Composition
Box B
Output B
Input B
Box A
Vertical Composition
Box B
Box A ⊗ B
id-Box
Identity
Braiding \ Symmetry
Box B
X-box
Box A
General Composition
Box B
Box A % B
Box A
General Composition
Box B
Directed Acyclic Graph
A
B
C
D
E
Composed Graph
A
B
C
D
E
Functor
Box
Input
Output
Injections
Box A
Green Input
Injections
Orange Input
Purple Output
Cian Output
Green Output
Box A
Green Input
Monoidal Functor
Orange Input
Purple Output
Cian Output
Green Output

Box F(A)
F(Green)
F(Orange)
F(Purple)
F(Cian)
F(Green)
Box A
Composition Preservation
Box B


Box F(A)
Box F(B)
Box A
Composition Preservation
Box B


Box F(B) • F(A)
Box A
Composition Preservation
Box B

Box F(B • A)
Composition Preservation

Box F(Id)
Composition Preservation
Box Id
Symmetry Preservation
Box B

F(X)-Box
Symmetry Preservation
Box B
X-Box
Vertical Composition Preservation
Box A
Box B


F(A) ⊗ F(B)
Vertical Composition Preservation
Box A
Box B

F(A ⊗ B)
General composition preservation
A
B
C
D
E





General composition preservation
A
B
C
D
E

Natural transformation
Box A
Between Functors
Box B


F(A)
G(B)
Box A
Natural link Between Functors
Box B


F(A)
G(B)
ζ: F ⟶ G
Box A
Natural link Between Functors
Box B


F(B • A)
G(id)
ζ: F ⟶ G
Box A
Natural link Between Functors
Box B


F(A)
G(B)
ζ: F ⟶ G
Box A
Natural link Between Functors
Box B


F(id)
G(B • A)
ζ: F ⟶ G
Box A
Natural link Between Functors
Box B


F(A)
G(B)
ζ: F ⟶ G
Example
Example
Universe 1:
Scala Functions and Serializable Types
Example
Universe 2:
Microservices
Universe 1:
Scala Functions and Serializable Types
Example
Universe 2:
Microservices
Deploy
as
JSON
REST
service
Universe 1:
Scala Functions and Serializable Types
Example
Universe 2:
Microservices
Deploy
as
JSON
REST
service
Deploy
as
Protobuf
batch
service
Universe 1:
Scala Functions and Serializable Types
Example
Deploy
as
JSON
REST
service
Deploy
as
Protobuf
batch
service
Poll JSON REST service
continiusly
collecting batches
Universe 2:
Microservices
Universe 1:
Scala Functions and Serializable Types
What serverless ACT framework could do ?
- Automatically detect connections between deployed functions in batches or in RESTs, fusing them into single service
- Automatically move functions from REST part to batch mode if this considered more effective
- Scale microservices according to downstream requirements
What can we bind?
- Pure functions
- Async effectful functions
- Probabalistic functions
- Reactive streams
- REST-services
- Batch & Stream processing
- Event-sourced services
- Views and aggregations
- Distributed transactions
- Deployments
- Sandboxes
- Visualizations
- Telemetry & Control
There's much more
- Compact closed categories - one way of enabling cycles
- Multiple monoidal products - more ways to compose
- Cartesian and cocartesian categories - for automatic fan-out and fan-in
- Higher dimensional categories for multilevel analysis and composition
- Enrichments for measurements and additional operations on elements
- Universal and couniversal structures
- Monoid- , comonoid- and other algebraic objects
Optics
Optic
To-Box
From-Box
in X
out X
out Y
in Y
Middle State M
Optic horizontal composition
To-Box A
From-Box A
in X
out X
out Y
in Y
Middle State M
To-Box B
From-Box B
in Y
out Y
out Z
in Z
Middle State N
Optic horizontal composition
To-Box A
From-Box A
in X
out X
Y
Middle State M
To-Box B
From-Box B
Y
out Z
in Z
Middle State N
Optic vertical composition
To-Box A
From-Box A
in X
out X
out Y
in Y
Middle State M
To-Box B
From-Box B
in U
out U
out V
in V
Middle State N
Optic vertical composition
To-Box A
From-Box A
in X
out X
out Y
in Y
Middle State M
To-Box B
From-Box B
in U
out U
out V
in V
Middle State N
Optic: example
Apply operation
Undo operation
request
source request
response
source response
Additional data
initial state
result state
initial state
result state
SAGA Optics
Create Order
Book items
Create payment method
Pay
Deliver
Validate address
Pack
Monoidal Categories
Linear types
Monoidal Categories
Box A
Input X
Output Y
def A(x: X): YBox
in U
Monoidal Category
Box A
in V
out X
out Y
out Z
def A(u: U, v: V): (X, Y, Z)in U
Monoidal Category
Box A
in V
def A(u: U, v: V): ()Box A
General Composition
Box B
Box С
def C(s: S, t: T, u: U): (X, Y) =
val (x, v, w) = A(s, t)
val y = B(w, v, u)
return (x, y)S
T
U
X
W
V
Y
General Composition
def paymentSaga(
orderData: OrderData,
paymentInfo: PayInfo,
address: Address
) : DeliveryFinished = {
val order = createOrder(orderData)
val booked = bookItems(order)
val payM = createPayMethod(paymentInfo)
val paidItems = pay(booked, payM)
val packedOrder = pack(paidItems)
val validAddress = validateAddress
deliver(packedOrder, validAddress)
}Create Order
Book items
Create payment method
Pay
Deliver
Validate address
Pack
Compile to (and from) categories
- We can represent any directed acyclic graph as a code
- We can compile any code into a directed acyclic graph
- We can work and reuse "open" graphs
- We can (type) check connectios in graphs
- We can check composability via the "exactly one use" rule
- We can represent functors and natural transformations as "generic" constructs
- We can compile normal scala code using macros into code-defined structures, representing universes
We can make

the language for ACT

deck
By Oleg Nizhnik
deck
- 368


