Coupling hydrodynamics and radiation calculations for star-jet interactions in agn
v. bosch-ramon, X. paredes-fortuny, D. khangulyan and M. perucho
La Plata, 7th October 2015
V. M. DE LA CITA
contribution of stars and their winds to
agn high-energy emission.
- We study a single star-jet interaction under different conditions: magnetic field and observational angle.
- We get luminosities that can contribute significantly to the high energy emission of AGN jets interacting with stars .
- The result confirms the first estimates by Bosch-Ramon 2015 and proposes a source of inverse Compton and synchrotron emission in AGN jets.
Bednarek & Protheroe 1997; Barkov et al. 2010, 2012; Khangulyan et al. 2013;
Bosch-Ramon et al. 2012; Araudo et al. 2013; Bosch-Ramon 2015;
Bednarek & Banasinski 2015
physical scenario
The impact of stars and its atmospheres on the AGN jets has been studied previously by other authors.
A number of problems must be addressed: the type of star populations, the impact of the stars in the jet dynamics...
We perform hydrodinamic simulations ot the regions close to the star, and then we compute its non-thermal emission.
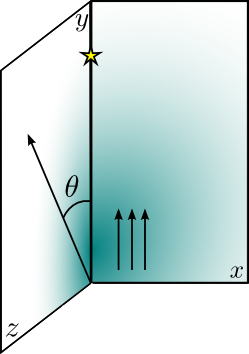
We fix our coordinate system with the y axis in the line connecting the base of the jet and the star. The shock is formed where the ram pressures of the two winds are balanced.
Our workframe
\vec{v}_\text{stellar wind} = 2000 \text{ km s}^{-1}
\dot{M}_\star = 10^{-9} M_\odot \text{yr}^{-1}
The stellar wind is uniform with the thrust of a high mass star with low mass rate (a thrust also typical for red giants) with the following data:
The jet has a luminosity of:
and a wind Lorentz factor of:
L_\text{jet} \sim 10^{44}\text{ erg s}^{-1}
\Gamma = 10
for a 1 pc radius
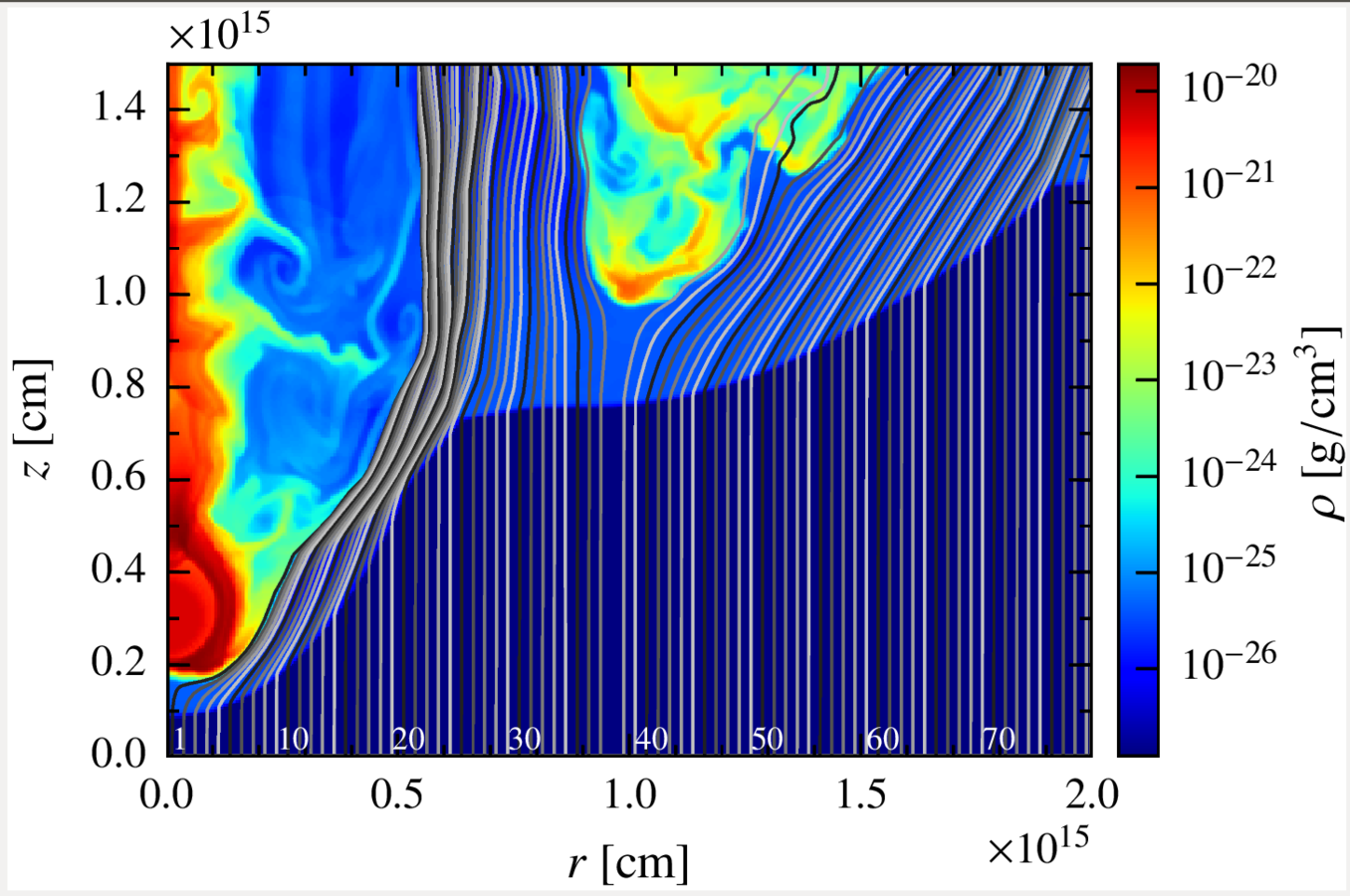
Going into details. hidrodynamic setup.
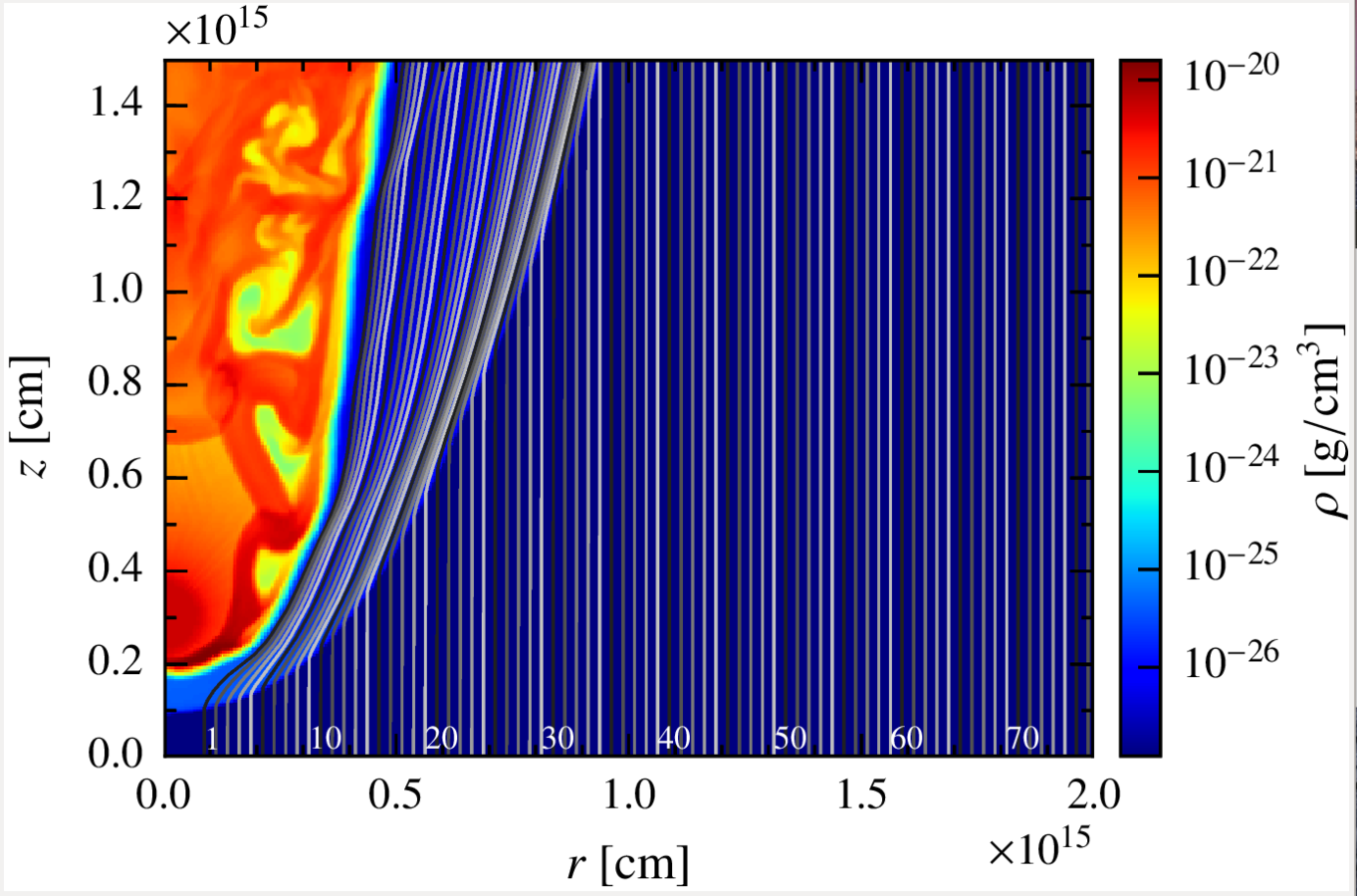
The fluid is divided in 77 lines with 200 cells each, describing an axisymmetric 2D space of:
r\in[0,2\times10^{15}\text{ cm}]
y\in[0,1.5\times10^{15}\text{ cm}]
y_\star = 3\times 10^{14} \text{ cm}
Star
Jet thrust
Although the RHD simulation is 2D, we take this information and scramble the different lines around the y axis, giving each cell a random azimuthal angle phi, so the result is more similar to the 3D real scenario.
Going into details. 3d emitter.
physical scenario. A single star
Inner parsec of Centaurus A
Müller, C. et al. 2014
Going into details. Physical assumptions i.
We follow a prescription for particle acceleration in strong shocks. The acceleration timescale goes like ~1/v² as proposed in previous works (e.g. Drury 1983)
We inject non-thermal particles when a shock takes place:
Internal energy goes up
and
fluid velocity goes down
Where and how do we inject non-thermal particles
Q(E) \propto E^{-2} \times (e^{-E_{min}/E})^5 \times e^{-E/E_{max}}
t'_\text{acc}=\eta E'qB'c, \text{with}
\eta = 2\pi (c/v)^2
Going into details. Physical assumptions ii.
Magnetic field perpendicular to the fluid line
\dfrac{B_0^{\prime 2}}{4\pi} = \chi_B (\rho_0h_0c^2)
B_k^\prime = B_0^\prime \Big( \dfrac{\rho_k v_0\Gamma_0}{\rho_0 v_k \Gamma_k}\Big)^{1/2}
\chi_B = 10^{-4}, 1
Definition of the magnetic field at the beginning of the line:
Evolution of the B field in the different cells k:
(Low, high magnetic field)
Fraction of matter energy flux that goes to magnetic energy
Photon field:
T_{\star} = 3\times 10^3 \text{ K}
L_{\star} = 3\times 10^{36} \text{erg s}^{-1}
Going into details. some notes on the code.
- We let the particles evolve until they reach a steady state so we can consider the medium stationary, in other words, every loss time (e.g. synchrotron) or cell-crossing time is much shorter than the dynamical time on large scales.
- All the computation is done in the (relativistic) frame of the fluid, so every relevant quantity has to be transformed, including the angles between fluid, gamma photons and target photons velocities.
- Once we have the electron distribution, we compute the inverse Compton (IC) and synchrotron radiation, taking into account the Doppler boosting.
\delta = 1/\Gamma(1-\beta\cos{\theta_\text{obs}})
\epsilon L(\epsilon)= \delta^4\epsilon'L(\epsilon')
where
Going into details. Observer angle.
To sample all the possibilities, we take four angles: 0º (with the jet bulk velocity pointing at the observer), 45º, 90º (when the observer is placed in the z axis) and 135º.
The observer will be placed beyond the star forming an angle theta with the vertical axis.
Star
Jet thrust
\theta = 0^\circ, 45^\circ, 90^\circ, 135^\circ
Results. Low magnetic field, steady state.
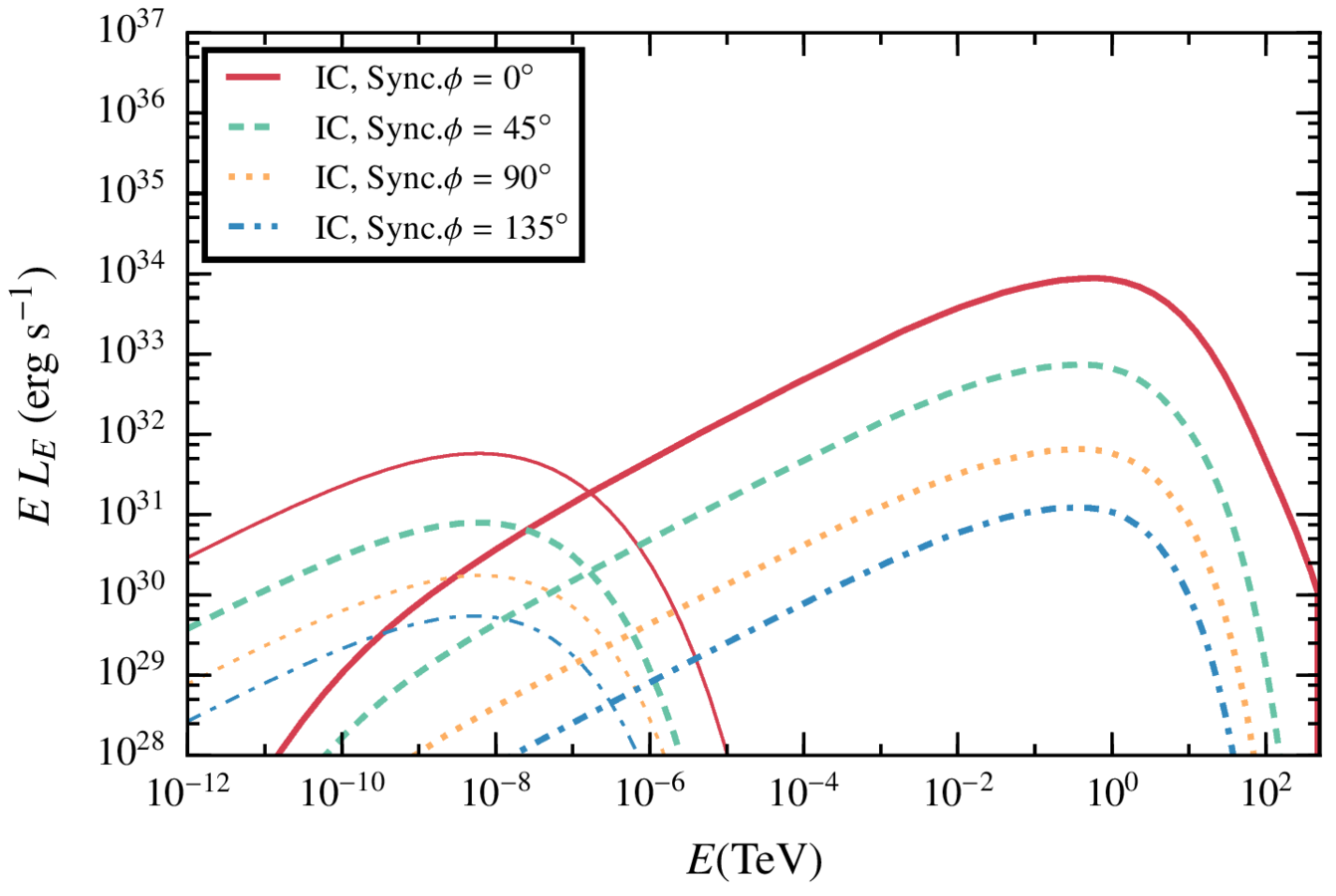
In the case of a low magnetic field, the IC radiation dominates the spectrum.
The difference between the four angles come from the doppler boosting, more important for smaller angles given that most of the cells have a strong y- component of the velocity
\chi_B = 10^{-4}
Results. high magnetic field, steady state.
In this case the synchrotron dominates the spectrum, while the IC is very similar.
\chi_B = 1
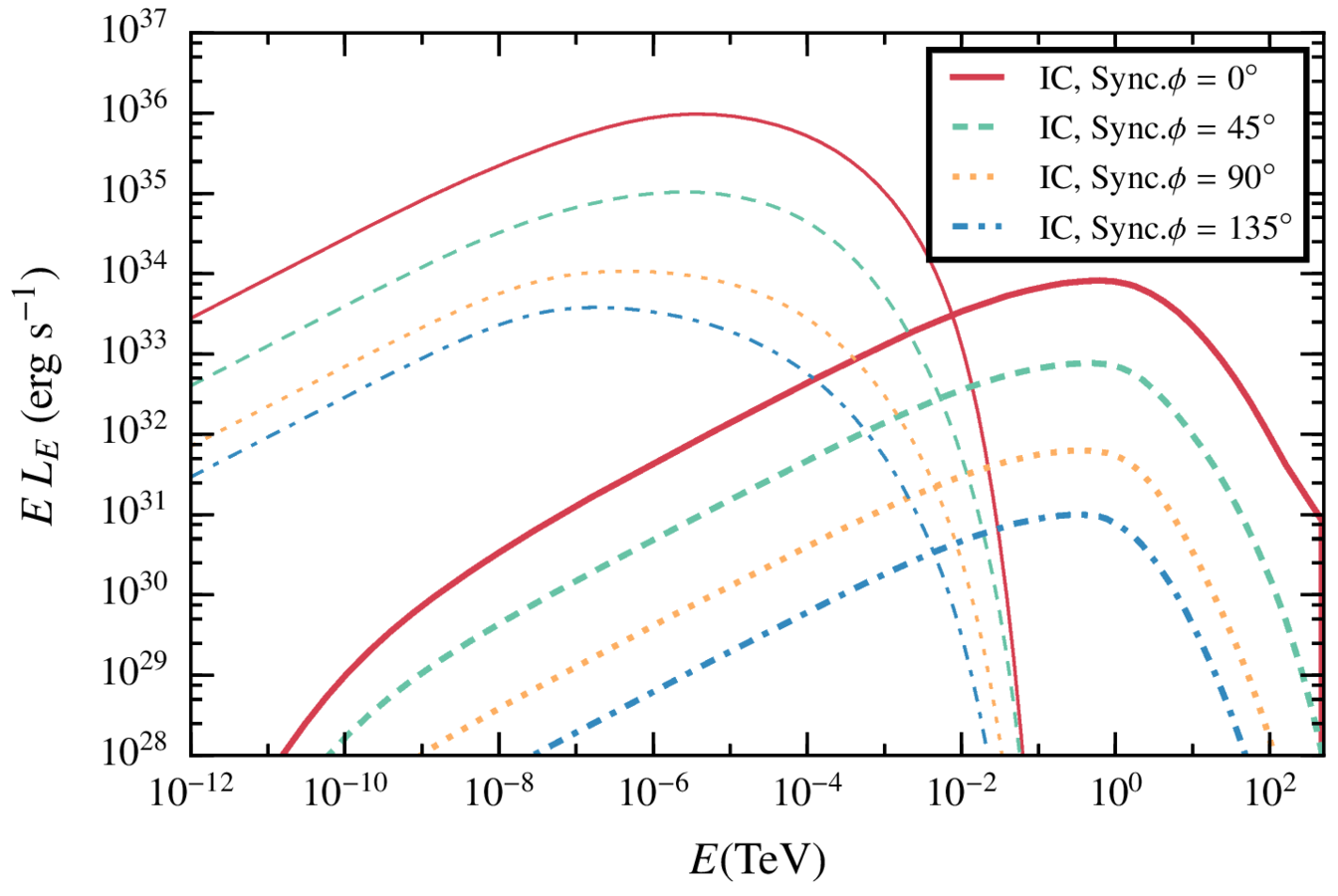
Synchrotron emission can play an important role at GeV energies even with not-so-extreme magnetic fields.
Results. perturbed state.
In some cases, the instabilities can eventually lead to a perturbed state of the shock, increasing the effective area of the emitter.
Results. perturbed state with with different B fields and angles
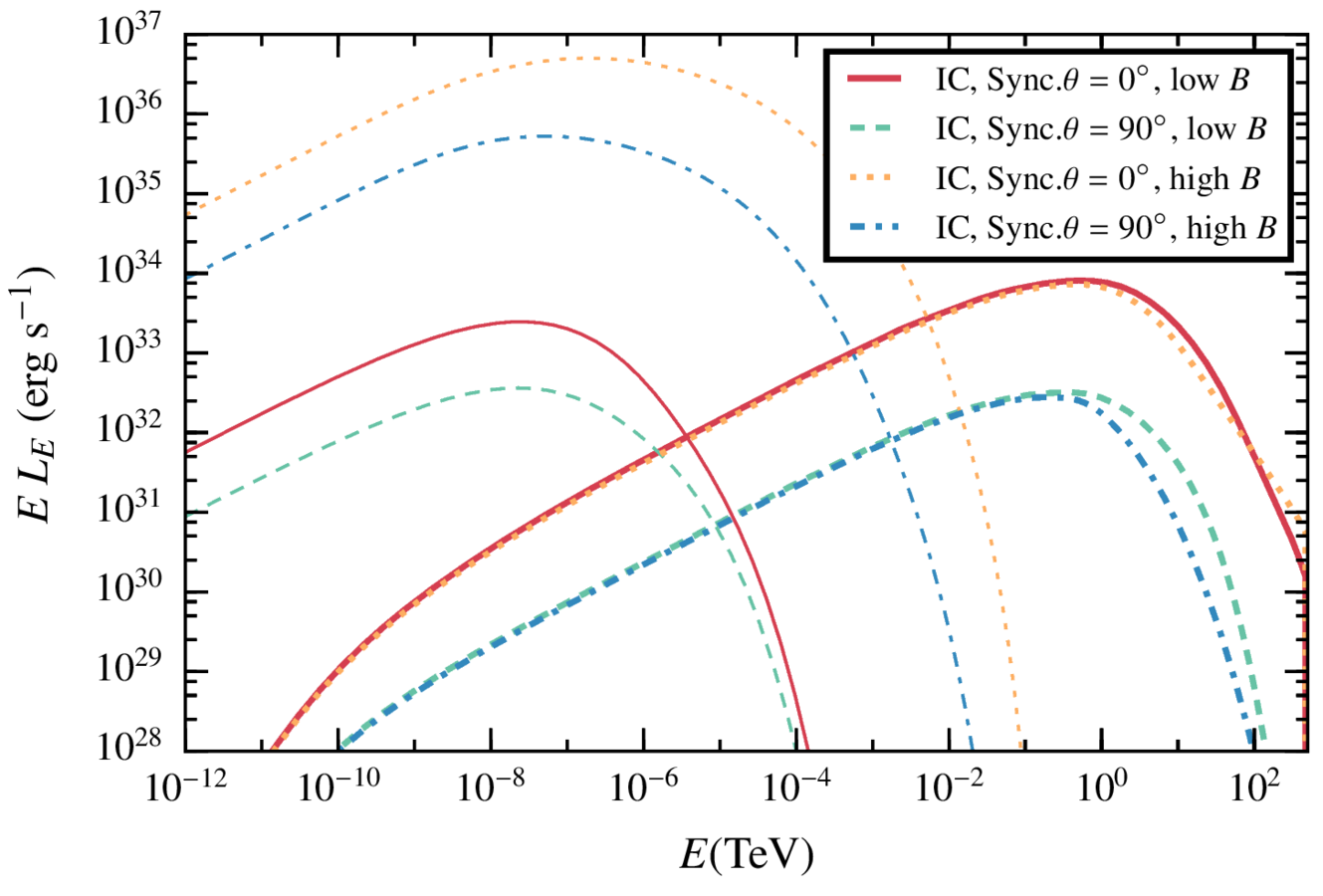
When the instabilities lead to a perturbed state of the shock, a transient increment of the synchrotron luminosity is expected.
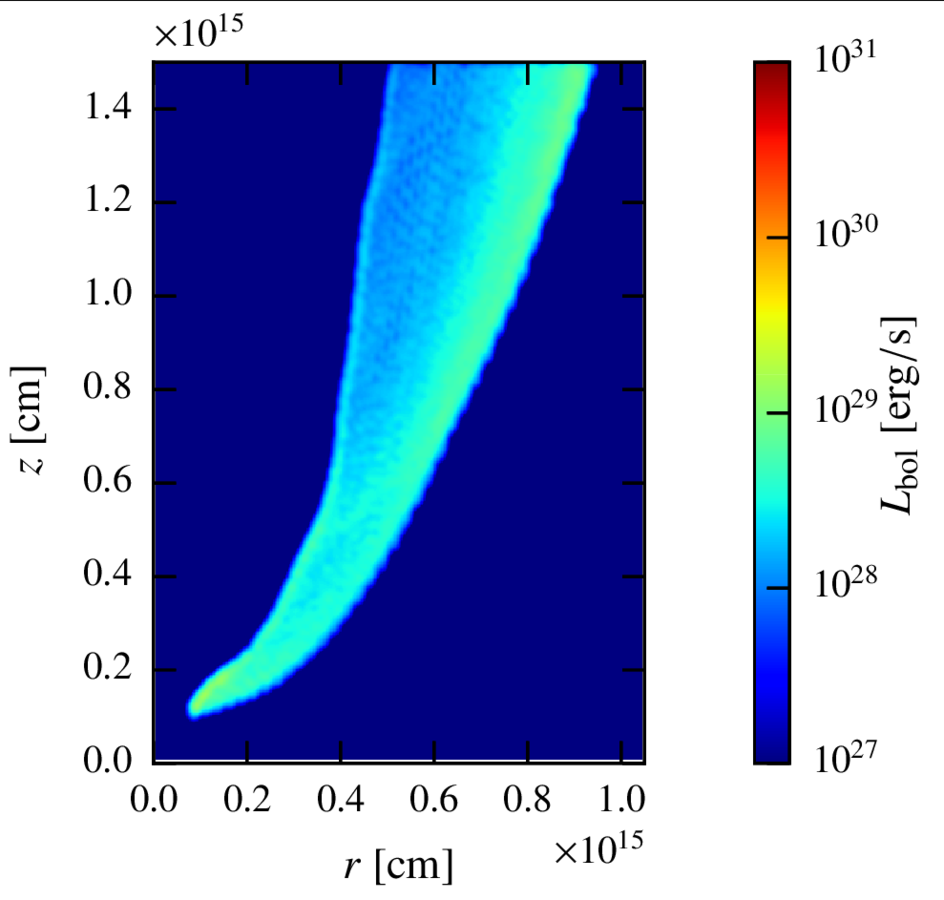
Maps. Steady state.
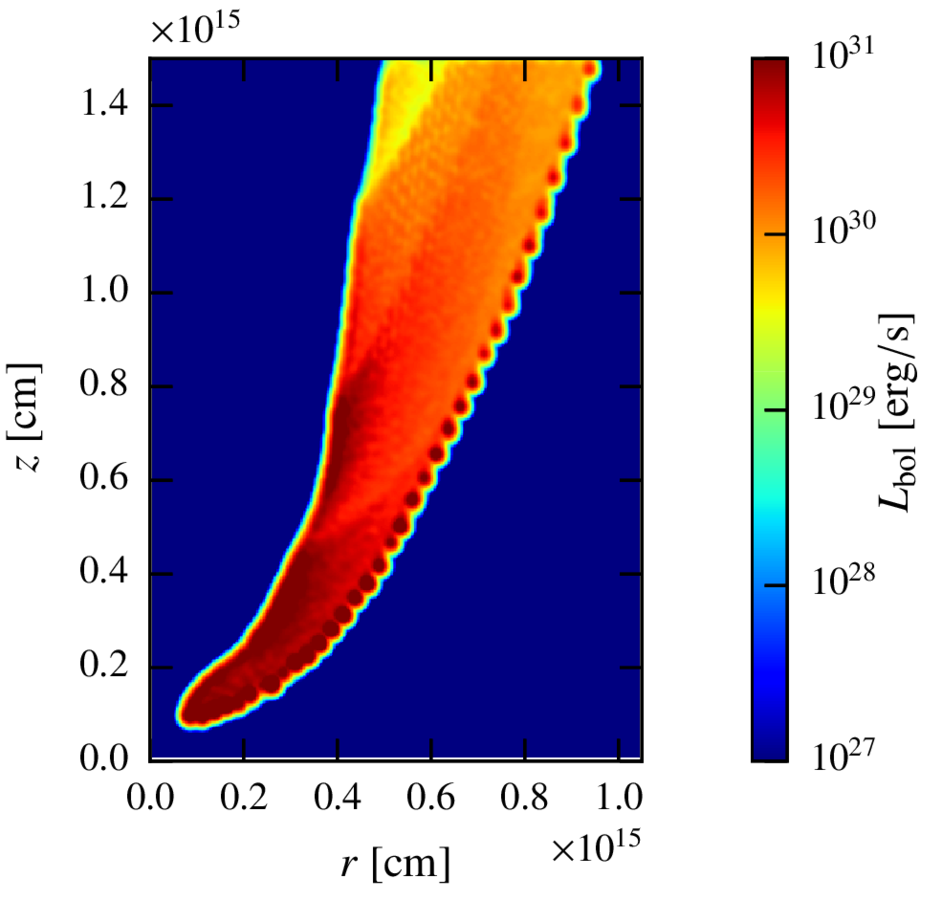
Inverse compton
The total observer luminosity in this case is:
r < r_{CD}
\chi_B = 10^{-4},\,\,\theta = 0^\circ
Whereas the luminosity of the region with
L_{IC}=5 \times 10^{34} \text{erg s}^{-1}
is ~100 times smaller, so the effective size of the emitter is much larger than the CD region.
Maps. Steady state.
synchrotron
The total observer luminosity in this case is:
For the synchrotron, the emission is even more equally distributed through the shock, because it does not depend on the external photon field.
L_{sync}=2.5 \times 10^{32} \text{erg s}^{-1}
\chi_B = 10^{-4},\,\,\theta = 0^\circ
Maps. perturbed state.
Inverse compton
synchrotron
\chi_B = 10^{-4},\,\,\theta = 0^\circ
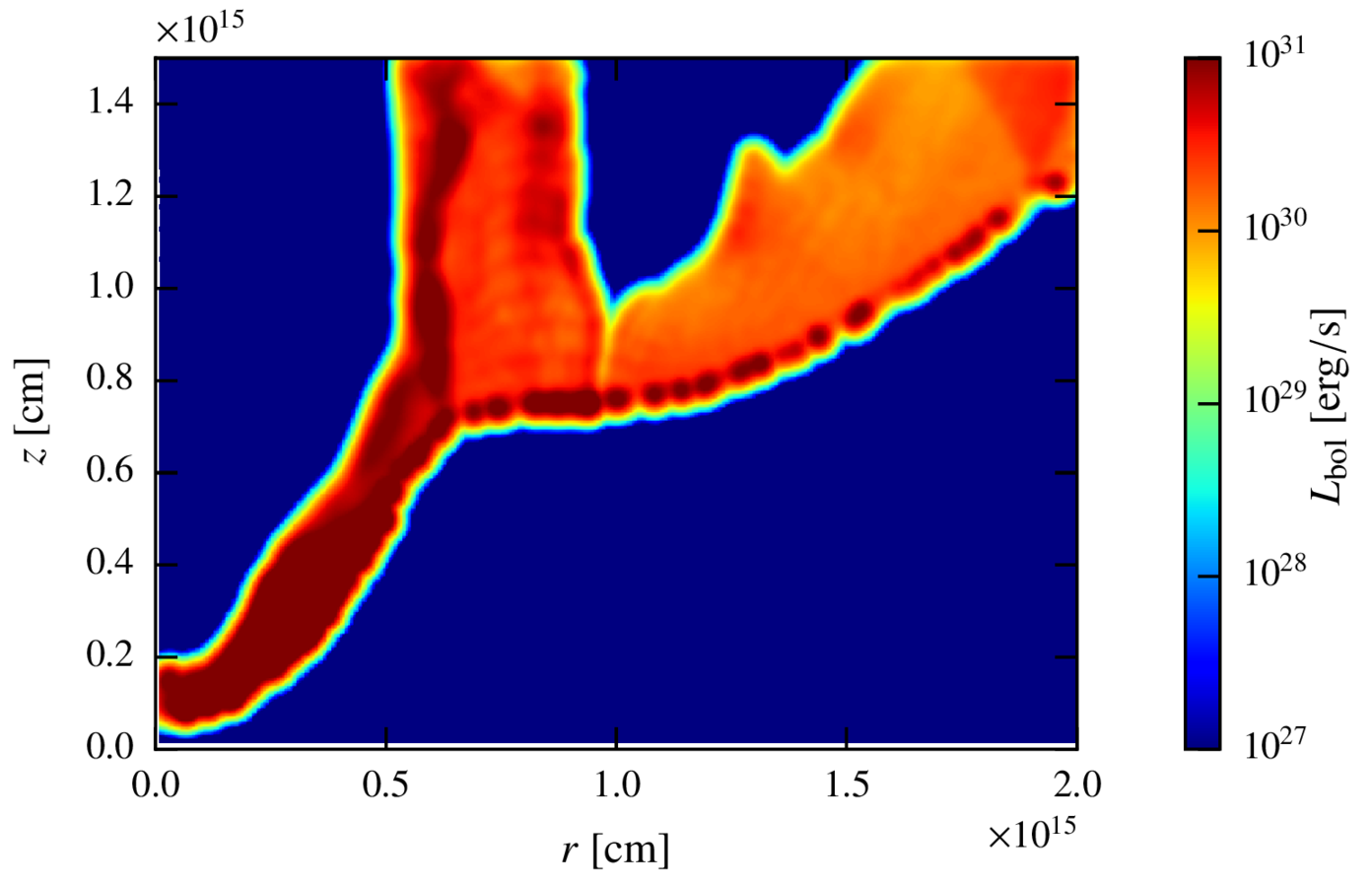
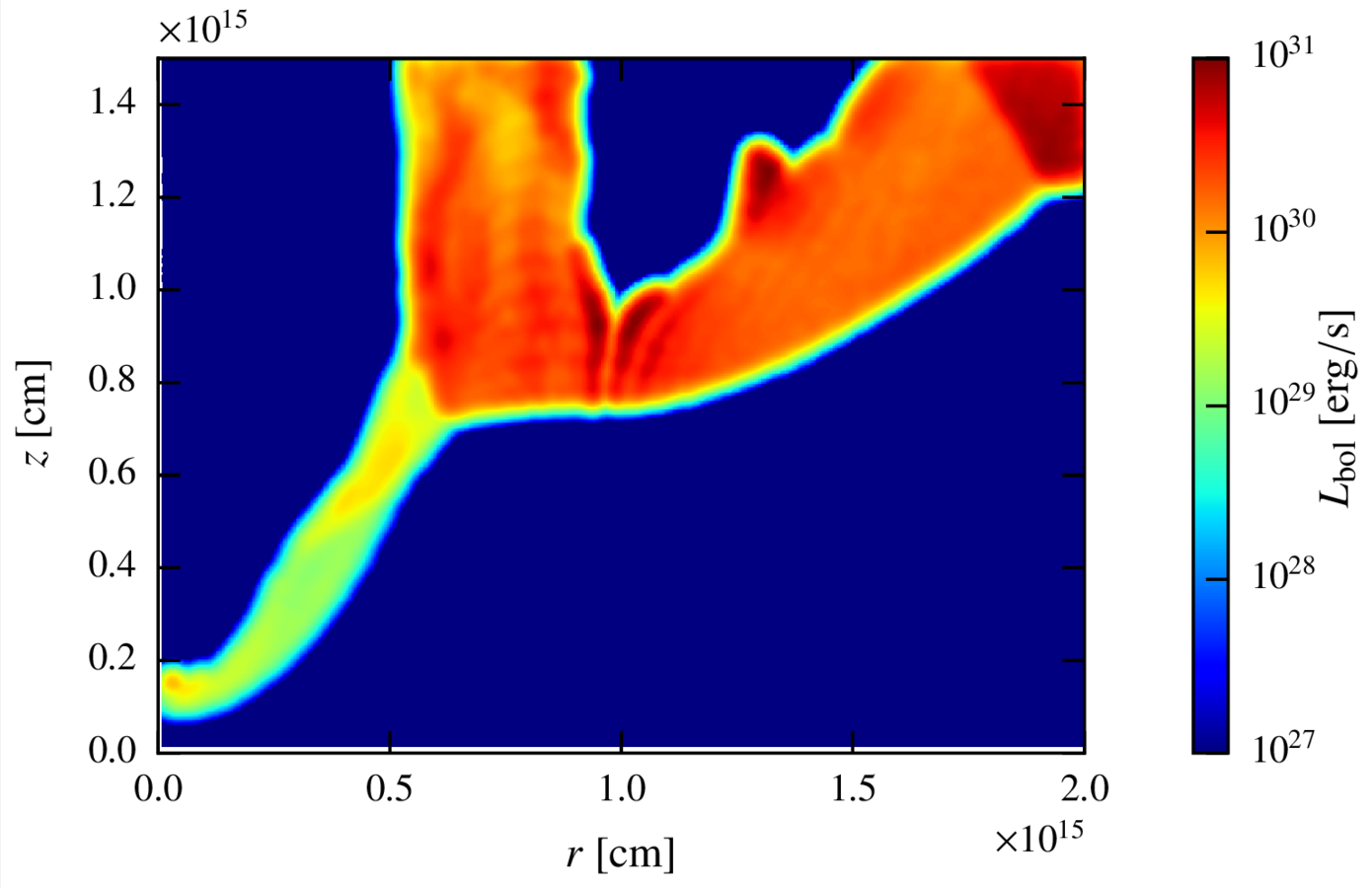
Discussion. Scalability of the results
\chi_B = 10^{-4},\,\,\phi = 0^\circ
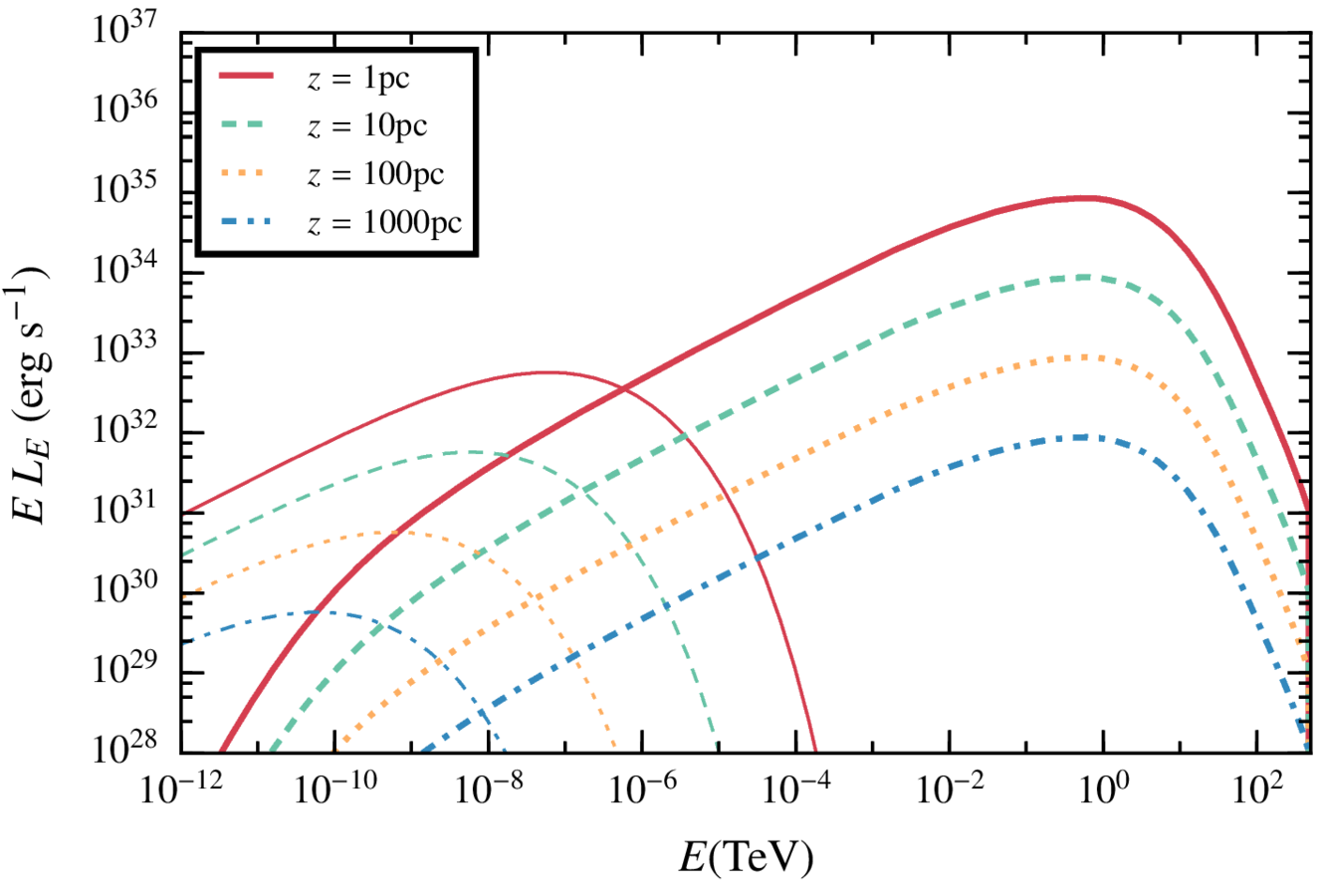
Our hydrodinamical simulation place the star at a jet height of z = 10pc, but the results can be easily scaled with z.
L_\text{rad}\propto 1/z
If the losses are dominated by escape:
Discussion. Conclusions.
- The effective radius of the emitter is much bigger than the contact discotinuity radius.
- Emission levels strongly depend on the viewer angle due to Doppler boosting.
- The non-thermal luminosity for a single star points towards potentially detectable luminosities for typical populations crossing AGN jets.
Thank You.
Backup slide. Fixing the line ending.
Given that the two winds can mix through the fluid lines, we have had to cut the lines at a certain point. To do so, we can impose that the amount of material that crosses the section do not get larger than a certain threshold:
\text{if: } S\rho v\Gamma > 2\times S_0\rho_0v_0\,\rightarrow\, \text{end of the line}
Backup slide. Injected Luminosity.
The injected non-thermal particles have a lumisosity given by a fraction of the generated internal energy per second in the cell.
L_{inj} = \chi_{NT} \times \dot{U}'_k =
With the pre-factor varying between 0 and 1 and the +/- subindexes refering to the right/left boundaries, respectively.
= \chi_{NT} v_k\Gamma_k^2\times \left(S_+\Gamma_+^2h_+\rho_+c^2\left(1 +\dfrac{v_+^2}{c^2}\right) - S_-\Gamma_-^2h_-\rho_-c^2\left(1 +\dfrac{v_-^2}{c^2}\right)\right)
HEPRO 2015
By otnoesmusica
HEPRO 2015
Coupling hydrodynamics and radiation calculations for star-jet interactions in AGN
