POJĘCIE ZŁOŻONOŚCI OBLICZENIOWEJ

określają miarę ilości zasobów komputerowych potrzebnych do wykonania danego algorytmu

• złożoność pesymistyczna - liczba zasobów komputerowych potrzebna przy wprowadzeniu "najgorszych" danych wejściowych,
• złożoność oczekiwana - liczba zasobów komp. potrzebnych przy wprowadzaniu "typowych" danych wejściowych.

PODZIAŁ ZE WZGLĘDU NA RODZAJE ZASOBÓW KOMPUTEROWYCH 

• Złożoność czasowa - mówi o tym, ile potrzebujemy instrukcji do rozwiązania problemu. Wyrażana jest liczbą tzw.  operacji dominujących, czyli takich, które mają bezpośredni wpływ na czas wykonywania algorytmu, np. dodawanie, odejmowanie, porównanie, zamiana. 
• Złożoność pamięciowa - określa, ile pamięci potrzeba do realizacji danej metody.

Złożoność czasowa i pamięciowa zależy od ilości wprowadzanych danych.

KLASY ZŁOŻONOŚCI

są to klasy funkcji algorytmów, które określają zależność czasu w realizacji obliczeń od rozmiaru danych wejściowych (dane pesymistyczne)

PRZYKŁADOWE KLASY ZŁOŻONOŚCI ALGORYTMÓW

a) złożoność stała - O(1), wykonywana jest stała liczba operacji oraz zużywana jest stała liczba komórek pamięci bez względu na rozmiar danych

b) złożoność logarytmiczna - O(logn)

c) złożoność liniowa - O(n), liniowa zależność czasu wykonania od ilości danych 

d) złożoność liniowo-logarytmiczna - O(n*logn)

e) złożoność kwadratowa - O(n^2), czas wykonania rośnie z kwadratem liczby przetwarzanych elementów

f) złożoność wykładnicza - O(2^n)

g) złożoność silnii - O(n!)

h) itd., itp. wszelkie, możliwe kombinacje powyższych

PORÓWNANIE KLAS ZŁOŻONOŚCI

Przy złożoności O(2*n), dla przykładowego zbioru danych wejściowych A={1,2,3,5,7,8} (czyli n=6), potrzebujemy 12 operacji, aby algorytm został wykonany.  

Nieważne, czy nasza złożoność wynosi 10000*O(n), czy 0.00001*O(n), i tak mówimy o złożoności liniowej.

O(n*logn) - to klasa algorytmów sortowania, które używamy.

Przykładowa inna złożoność to np. n*log(log(log(n))).

Informacje wstępne

    Przykład

Załóżmy, że pewien programista ma posortować 1000 plików [n]. Zna tylko algorytm o złożoności O(n^2). Dla ustalenia uwagi jego komputer ma procesor przetwarzający informację z częstotliwością 1GHz (to daje miliard operacji na sekundę [s]). Zatem w naszym przypadku:

O(n^2)              n = 1000 = 10^3          s = 10^9

Po podstawieniu danych otrzymamy:

O[(10^3)^2] = 10^6

Dzieląc to przez szybkość komputera otrzymamy czas równy:

T = 10^6/10^9 = 10^-3 s czyli 1 ms.

Stosunkowo dobry czas.

A co jeśli nasz informatyk będzie musiał posortować milion, lub nawet miliard plików, pracując ciągle na tym samym komputerze? Zatem:

a)O(n^2)               n = 10^6               s = 10^9

b)O(n^2)              n = 10^9               s = 10^9

Po podstawieniu otrzymamy:

a) O[(10^6)^2] = 10^12    T = 10^12/10^9 = 10^3 s (~ 15 min)

b) O[(10^9)^2] = 10^18    T = 10^18/10^9 = 10^9 s (~30 lat)

Przypadek a) jest jeszcze do zaakceptowania, ale z trudem.  Przypadek b) będzie trwać zdecydowanie za długo.Co możemy zrobić aby przyspieszyć ten proces?

Nasz informatyk dowiedział się, że można zastosować algorytmy o mniejszej złożoności.

           a)O[n*log10(n)]

           b)O(n)

Zobaczmy zatem jak będzie wyglądać czas wysyłania oferty dla miliona i miliarda wiadomości:

a)      O[10^6*log10(10^6)] = 10^6*6               T=6*10^6/10^9=6*10^-3 (6ms)

         O[10^9*log10(10^9)] = 10^9*9               T=9*10^9/10^9=1 (9 s)

b)       O(10^6) = 10^6                                         T=10^6/10^9=10^-3 (1ms)

           O(10^9) = 10^9                                         T=10^9/10^9=1 (1s)

Wybór właściwego algorytmu dla zadania jest kluczowy!

Zastosowanie właściwego algorytmu jest w stanie zredukować czas przetwarzania o całe rzędy wielkości. W naszym przypadku z kilkudziesięciu lat do kilku sekund.

WŁAŚCIWOŚCI NOTACJI "duże O"

W prostych przypadkach arytmetyka na notacji "duże O" (analogicznie dla notacji "małe o") jest intuicyjna, np.:

W ogólności zaś należy być bardzo ostrożnym gdyż np. uproszczenie  

do            nie jest zdefiniowane. Wynika to z nieliniowości logarytmów.

PRZYKŁADY - notacja "duże O"

                                                   zapis w zależności od wymaganej

dokładności oszacowań:

<=>

STANDARDOWE SZACOWANIE

– funkcja          jest ograniczona, np.:

                              – funkcja          jest ograniczona przez funkcję

logarytmiczną

                        – funkcja          jest ograniczona przez funkcję

liniową

                            – funkcja           jest ograniczona przez funkcję potęgową lub wielomian

                     – funkcja            jest ograniczona przez funkcję 

wykładniczą

 – funkcja          jest ograniczona przez silnię

SORTOWANIE BĄBELKOWE

ang. bubble sort

Za pomocą tego algorytmu sprawdzamy całą tablicę od końca. Jeżeli trafimy na parę elementów, w której większy poprzedza mniejszy, to zamieniamy je miejscami i znów zaczynamy przeszukiwać tę tablicę od końca.

Czynność jest powtarzana do czasu, gdy podczas sprawdzania całej tablicy nie zajdzie ani jedna zamiana elementów.

Algorytm nosi nazwę bąbelkowy, gdyż najmniejsze liczby "wypływają" z dołu tablicy na jej szczyt.

SORTOWANIE BĄBELKOWE

ang. bubble sort

Klasa złożoności O(n^2).

Sprawdzane są elementy już posortowane, dlatego też sporą wadą tego algorytmu są tzw. puste przebiegi.

Możemy go poprawić zapamiętując za każdym razem indeks tablicy, od którego liczby są już uporządkowane. Oczywiście przyspieszy to konkretną implementację algorytmu, ale w ogólności i tak nie zmieni to klasy algorytmu O(n^2-n) = O(n^2).

PRZYKŁADOWY ZAPIS ALGORYTMU SORTOWANIA BĄBELKOWEGO

#include <iostream>
#include <vector>

using namespace std;

void bubble_sort(vector<int> & v);

int main(){
    vector<int> v = {342,5356,234,567,72,4326,423,536,324};
    bubble_sort(v);

    for (auto elem : v) {
	cout << elem << " ";
    }
    return 0;
}

PRZYKŁADOWY ZAPIS ALGORYTMU SORTOWANIA BĄBELKOWEGO

void bubble_sort(vector<int> & v){
    bool byla_zamiana;

    while(byla_zamiana){

        byla_zamiana = false;
        
        for(int i = 1; i<v.size(); i++){
            
            if(v[i] < v[i - 1]){
                int zmienna_pomocnicza = v[i];
                v[i] = v[i-1];
                v[i-1] = zmienna_pomocnicza;

                byla_zamiana = true;
            }
        }
    }
}

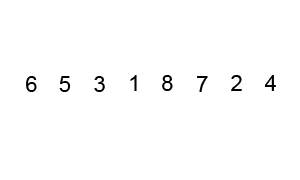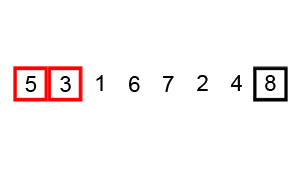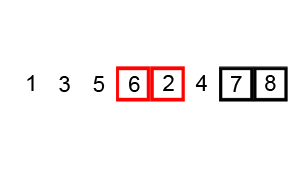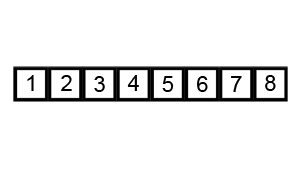
Obrazek z Wikipedia Creative Commons Attribution-ShareAlike License

SORTOWANIE PRZEZ WSTAWIANIE

ang. insertion sort

Idea działania tego algorytmu opiera się na podziale ciągu na dwie części: pierwsza jest posortowana, druga jeszcze nie. Wybieramy kolejną liczbę z drugiej części i wstawiamy ją do pierwszej. Ponieważ jest ona posortowana to szukamy dla naszej liczby takiego miejsca, aby liczba na lewo była niewiększa, a liczba na prawo niemniejsza. 

Zasada działania tego algorytmu jest często porównywana do porządkowania kart w wachlarz podczas gry.

SORTOWANIE PRZEZ WSTAWIANIE

ang. insertion sort

Złożoność tego algorytmu również jest kwadratowa O(n^2) -> wstawanie liczby do posortowanej tablicy wymaga czasu O(n), lecz w przypadku częściowo posortowanego ciągu możemy otrzymać złożoność liniową O(n) algorytmu.

Algorytm ten jest o wiele lepszy niż sortowanie bąbelkowe, ale w dalszym ciągu charakteryzuje się dość wysokim kosztem, co eliminuje go w praktyce z sortowania dużych tablic.

PRZYKŁADOWY ZAPIS ALGORYTMU SORTOWANIA PRZEZ WSTAWIANIE

void insertion_sort(std::vector<int> & v) {
	for (int i = 1;i<v.size();i++) {

		int wstawiany = v[i]; // aktualny element zapisujemy obok
		int j = i; // wszystkie na lewo od i są już posortowane

		for (;j> 0 && wstawiany < v[j - 1] ; j--) {
			v[j] = v[j - 1]; // przesuwamy - w ten sposób robimy miejsce dla 
							// aktualnie sortowanego elementu
		}
		v[j] = wstawiany;
		
	}
}

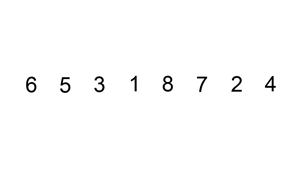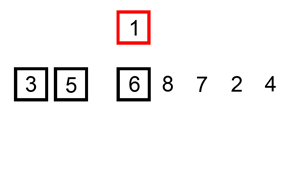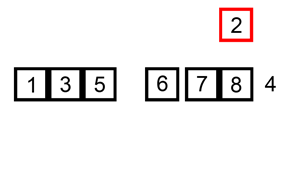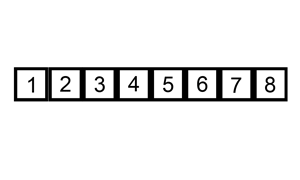
Obrazek z Wikipedia Creative Commons Attribution-ShareAlike License

SORTOWANIE SZYBKIE

ang. quicksort

Zostało wynalezione w 1962 roku przez Charles'a Anthony'ego Richard'a Hoare'a. Działa w oparciu o zasadę "dziel i zwyciężaj" (ang. divide and conquer).

Tony Hoare (ur. 11.01.1934 w Kolombo, Sri Lanka) - brytyjski informatyk, który w roku 1980 otrzymał nagrodę Turinga (odpowiednik Nobla w Informatyce), jako dowód uznania za wkład w rozwój języków programowania.

1. DZIEL -> dzielimy nasz zbiór danych na dwa podzbiory, które są niezależnie sortowane. Najważniejszy jest wybór piwotu, czyli miejsca podziału tablicy. Jest to tzw. element rozgraniczający, którym może być dowolny wyraz.

2. ZWYCIĘŻAJ ->

i. Przeglądamy tablicę od lewego końca, aż znajdziemy element większy niż rozgraniczający.

ii. Przeglądamy tablicę od prawego końca aż znajdziemy element mniejszy od rozgraniczającego.

iii. Zamieniamy te elementy miejscami i teraz powtarzamy algorytm sortowania osobno dla dwóch partycji dochodząc do tablic jednoelementowych.

wartości <=piwot       wartości >=piwot      PIWOT

                                                lewa partycja           prawa partycja

3. POŁĄCZ -> połączenie otrzymanych częściowych rozwiązań w rozwiązanie globalne.

"DZIEL I ZWYCIĘŻAJ!"

- Algorytm ten uważany jest za najszybszy dla danych losowych.

- Jest to algorytm niestabilny, dlatego też cechy elementów, które w trakcie sortowania nie były brane pod uwagę mogą zmienić swoją kolejność po sortowaniu.

- Algorytm ten w najgorszym przypadku ma złożoność kwadratową O(n^2), ale mimo to jest bardzo często stosowany ze względu na swoją niską liniowo-logarytmiczną złożoność (O(n*ln(n) ) w średnim przypadku.

SORTOWANIE SZYBKIE cd.

ang. quicksort

GRAFICZNE PRZEDSTAWIENIE ALGORYTMU

SORTOWANIA

SZYBKIEGO

GRAFICZNE PRZEDSTAWIENIE ALGORYTMU SORTOWANIA SZYBKIEGO nr 2

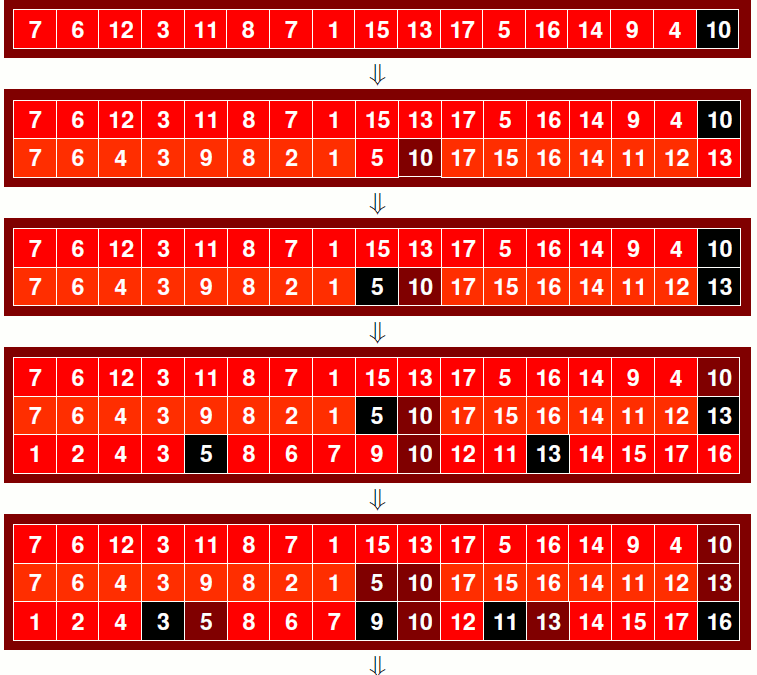
GRAFICZNE PRZEDSTAWIENIE ALGORYTMU SORTOWANIA SZYBKIEGO nr 2 cd.

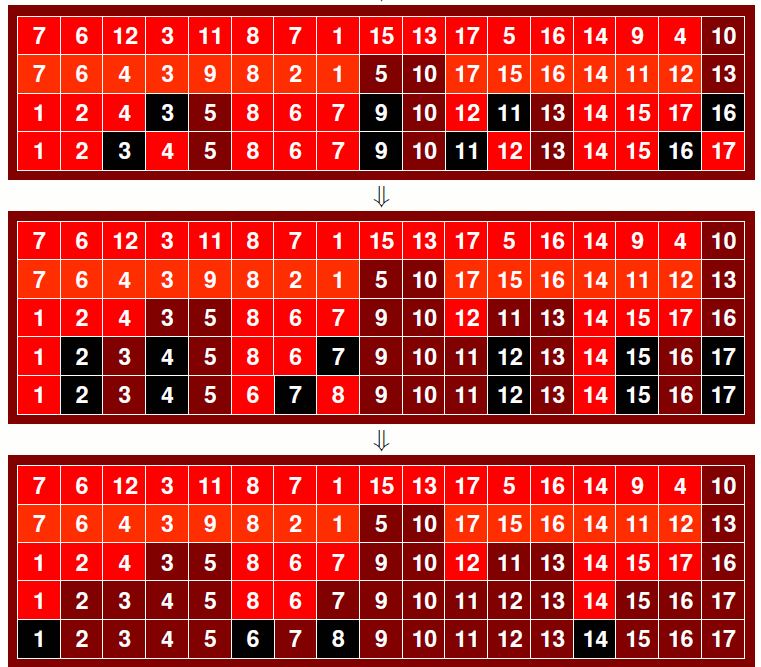
#include <iostream>
#include <vector>

using namespace std;

void quicksort(vector<int> & v);

int main(){
    vector<int> v = {342,5356,234,567,72,4326,423,536,324};
    quicksort(v);

    for (auto elem : v) {
	cout << elem << " ";
    }
    return 0;
}

#include <iostream>
#include <vector>

using namespace std;

void quicksort(vector<int> & v);
void quicksort(vector<int> & v,int left,int right);

int main(){
    vector<int> v = {342,5356,234,567,72,4326,423,536,324};
    quicksort(v);

    for (auto elem : v) {
	cout << elem << " ";
    }
    return 0;
}

void quicksort(vector<int> & v) {
	quicksort(v, 0, v.size() - 1);
}

#include <iostream>
#include <vector>

using namespace std;

void quicksort(vector<int> & v);
void quicksort(vector<int> & v,int left,int right);
int partition(vector<int> & v, int left, int right);

int main(){
    vector<int> v = {342,5356,234,567,72,4326,423,536,324};
    quicksort(v);

    for (auto elem : v) {
	cout << elem << " ";
    }
    return 0;
}

void quicksort(vector<int> & v) {
    quicksort(v, 0, v.size() - 1);
}

void quicksort(vector<int> & v, int left, int right) {

    // dzielimy wektor na dwie części, pivot to indeks podziału
    int pivot = partition(v, left, right); 
    quicksort(v, left, pivot);
    quicksort(v, pivot + 1, right);
}

#include <iostream>
#include <vector>

using namespace std;

void quicksort(vector<int> & v);
void quicksort(vector<int> & v,int left,int right);
int partition(vector<int> & v, int left, int right);

int main(){
    vector<int> v = {342,5356,234,567,72,4326,423,536,324};
    quicksort(v);

    for (auto elem : v) {
	cout << elem << " ";
    }
    return 0;
}

void quicksort(vector<int> & v) {
    quicksort(v, 0, v.size() - 1);
}

void quicksort(vector<int> & v, int left, int right) {
    if (left < right) { // warunek stopu algorytmu, już nie ma co dzielić
        // dzielimy wektor na dwie części, pivot to indeks podziału
	int pivot = partition(v, left, right); 
	quicksort(v, left, pivot);
	quicksort(v, pivot + 1, right);
    }
}

// dzielimy wektor na dwie części, w pierwszej wszystkie liczby są <= x, w drugiej >x
int partition(vector<int> & v, int left, int right){
    //...
}

// dzielimy wektor na dwie części, w pierwszej wszystkie liczby są <= x, w drugiej >x
int partition(vector<int> & v, int left, int right) {
    // obieramy piwot (element podziału) jako pierwszy element wektora
    // może być dowolny inny, ale jakiś musimy przyjąć
    int pivot = v[left];

    // przesuń elementy mniejsze od pivota na lewo, większe na prawo
}

// dzielimy wektor na dwie części, w pierwszej wszystkie liczby są <= x, w drugiej >x
int partition(vector<int> & v, int left, int right) {
    // obieramy piwot (element podziału) jako pierwszy element wektora
    // może być dowolny inny, ale jakiś musimy przyjąć
    int pivot = v[left];
    
    int i = left, j = right; // i, j = indeksy w wektorze do zamieniania
    
    // przesuń elementy mniejsze od pivota na lewo, większe na prawo
    // ...
}

// dzielimy wektor na dwie części, w pierwszej wszystkie liczby są <= x, w drugiej >x
int partition(vector<int> & v, int left, int right) {
    // obieramy piwot (element podziału) jako pierwszy element wektora
    // może być dowolny inny, ale jakiś musimy przyjąć
    int pivot = v[left];
    
    int i = left, j = right; // i, j = indeksy w wektorze do zamieniania
    
    while (true) { // pętla nieskończona - wychodzimy z niej tylko przez return j
        // dopóki elementy z prawego końca wektora są większe od pivota jest ok
        while (v[j] > pivot) {j--;}
        // dopóki elementy z lewego końca wektora są mniejsze od pivota jest ok
        while (v[i] < pivot) {i++;}
    
        // ...
    }
}

// dzielimy wektor na dwie części, w pierwszej wszystkie liczby są <= x, w drugiej >x
int partition(vector<int> & v, int left, int right) {
    // obieramy piwot (element podziału) jako pierwszy element wektora
    // może być dowolny inny, ale jakiś musimy przyjąć
    int pivot = v[left];
    
    int i = left, j = right; // i, j = indeksy w wektorze do zamieniania
    
    while (true) { // pętla nieskończona - wychodzimy z niej tylko przez return j
        // dopóki elementy z prawego końca wektora są większe od pivota jest ok
        while (v[j] > pivot) {j--;}
        // dopóki elementy z lewego końca wektora są mniejsze od pivota jest ok
        while (v[i] < pivot) {i++;}
    
        // elementy za indeksami i oraz j są po złej stronie, zamieniamy je miejscami
        if (i<j) { 
            // zamień miejscami 

            // ...
        }
    }
}

// dzielimy wektor na dwie części, w pierwszej wszystkie liczby są <= x, w drugiej >x
int partition(vector<int> & v, int left, int right) {
    // obieramy piwot (element podziału) jako pierwszy element wektora
    // może być dowolny inny, ale jakiś musimy przyjąć
    int pivot = v[left];
    
    int i = left, j = right; // i, j = indeksy w wektorze do zamieniania
    
    while (true) { // pętla nieskończona - wychodzimy z niej tylko przez return j
        // dopóki elementy z prawego końca wektora są większe od pivota jest ok
        while (v[j] > pivot) {j--;}
        // dopóki elementy z lewego końca wektora są mniejsze od pivota jest ok
        while (v[i] < pivot) {i++;}
    
        // elementy za indeksami i oraz j są po złej stronie, zamieniamy je miejscami
        if (i<j) { 
            int w = v[i];
            v[i] = v[j];
            v[j] = w;

            // ....
        }
    }
}

// dzielimy wektor na dwie części, w pierwszej wszystkie liczby są <= x, w drugiej >x
int partition(vector<int> & v, int left, int right) {
    // obieramy piwot (element podziału) jako pierwszy element wektora
    // może być dowolny inny, ale jakiś musimy przyjąć
    int pivot = v[left];
    
    int i = left, j = right; // i, j = indeksy w wektorze do zamieniania
    
    while (true) { // pętla nieskończona - wychodzimy z niej tylko przez return j
        // dopóki elementy z prawego końca wektora są większe od pivota jest ok
        while (v[j] > pivot) {j--;}
        // dopóki elementy z lewego końca wektora są mniejsze od pivota jest ok
        while (v[i] < pivot) {i++;}
    
        // elementy za indeksami i oraz j są po złej stronie, zamieniamy je miejscami
        if (i<j) { 
            int w = v[i];
            v[i] = v[j];
            v[j] = w;

            i++; // idź dalej
            j--;
        }
        // ...
    }
}

// dzielimy wektor na dwie części, w pierwszej wszystkie liczby są <= x, w drugiej >x
int partition(vector<int> & v, int left, int right) {
    // obieramy piwot (element podziału) jako pierwszy element wektora
    // może być dowolny inny, ale jakiś musimy przyjąć
    int pivot = v[left];
    
    int i = left, j = right; // i, j = indeksy w wektorze do zamieniania
    
    while (true) { // pętla nieskończona - wychodzimy z niej tylko przez return j
        // dopóki elementy z prawego końca wektora są większe od pivota jest ok
        while (v[j] > pivot) {j--;}
        // dopóki elementy z lewego końca wektora są mniejsze od pivota jest ok
        while (v[i] < pivot) {i++;}
    
        // elementy za indeksami i oraz j są po złej stronie, zamieniamy je miejscami
        if (i<j) { 
            int w = v[i];
            v[i] = v[j];
            v[j] = w;

            i++; // idź dalej
            j--;
        }
        else { // wszystkie elementy większe po prawej, mniejsze po lewej
               // kończymy, zwracamy miejsce podziału
	    return j;
	}
    }
}