Intro To

By Casey Allred

@sbditto85

Who am I?

• PHP Developer
• Haskell Hobbyist/Developer
• Father of two beautiful girls

Outline

• Compare to typical OOP language 'X'
• Functions!
• Types and Type Classes
• Lists
• Functor, Applicative, and Monads
• Monad Transformers
• Tools

Side note

How many of us know everything about electricity?

Haskell vs OOP

What's the same?

• Turing Complete

What's Different

• Everything Else

Why do I care about differences?

• Because you have to approach problems differently
• Need to forget typical OOP approaches
• Need to forget OOP jargon and learn FP jargon
• You will struggle

Functions!

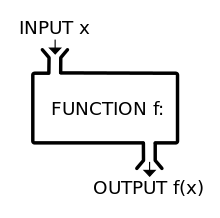
Functions

• "Bread and butter" of Haskell
• Behave like math function f(x) = x + 2 (stateless)
• Parameters separated by spaces
• Curried by default
• Can take or return other functions
• No Objects, so Data and Functions are separate
• Operators (+, -, ==, <$>) are functions too!

Hello World

module Main where

main :: IO ()
main = putStrLn "Hello World"

Hello World (Compared)

module Main where

main :: IO ()
main = putStrLn "Hello World"

//CPP from https://en.wikibooks.org/wiki/C%2B%2B_Programming/Examples/Hello_world

#include <iostream>
 
int main()
{
  std::cout 
    << "Hello World!" 
    << std::endl;
  return 0;
}

Addition

module Main where

main :: IO ()
main = print (addInt 3 4)

addInt :: Int -> Int -> Int
addInt x y = x + y

addThree :: Int -> Int
addThree = addInt 3

Addition

module Main where

main :: IO ()
main = print (addInt 3 4)

addInt :: Int -> Int -> Int
addInt x y = x + y

--To call a function
x `addInt` y   -- is infix
addInt x y     -- is prefix

x + y          -- is infix
(+) x y        -- is prefix

Addition (Compared)

addInt :: Int -> Int -> Int

addInt x y = x + y

int addInt(int x, int y) {

    return x + y;

}

Fibonacci

The formula for the Fibonacci sequence is:

Fn = F(n-1) + F(n-2)

with F(0) = 0 and F(1) = 1

Fibonacci

module Main where

main :: IO ()
main = print (fibN 10)

fibN 0 = 0
fibN 1 = 1
fibN n = fibN (n-1) + fibN (n-2)


-- Output: 55

Fibonacci

module Main where

main :: IO ()
main = print (fibN 10)

fibN :: (Eq a, Num a) => a -> a
fibN 0 = 0
fibN 1 = 1
fibN n = fibN (n-1) + fibN (n-2)

Fibonacci

module Main where

main :: IO ()
main = print (fibN 10)

fibN i =
    (head . drop i) fibs

fibs = 
    0 : 1 : zipWith (+) fibs (tail fibs)

Function Composition

• In math you would do: 
• executes right to left
• types must line up

funOne :: Int -> String

funTwo :: String -> Bool

combined :: Int -> Bool
combined x = (funTwo . funOne) x

Factorial

module Main where

main :: IO ()
main = print (factorial 5)

factorial 1 = 1
factorial n = n * factorial (n - 1)

{-
OUTPUT: 120
-}

factorial 1 = 1

factorial n = n * factorial (n-1)

Factorial

module Main where

main :: IO ()
main = print (factorial 5)

factorial n = product [1..n]

{-
OUTPUT: 120
-}

Factorial

module Main where

main :: IO ()
main = print (factorial 5)


factorial :: (Enum a, Num a) => a -> a
factorial n = product [1..n]

{-
OUTPUT: 120
-}

FizzBuzz

module Main where

import Control.Monad
import Lib

main :: IO ()
main = forM_ fizzBuzz putStrLn

module Lib
    ( fizzBuzz
    ) where

fizzBuzz :: [ String ]
fizzBuzz =
  map fizzInt [1..100]
  where
    fizzInt :: Int -> String
    fizzInt i =
      case (i `mod` 3 == 0, i `mod` 5 == 0) of
         (True, True) -> "FizzBuzz"
         (True, False) -> "Fizz"
         (False, True) -> "Buzz"
         (False, False) -> show i

Divisible by 3 put "Fizz"

Divisible by 5 put "Buzz"

Otherwise put the number

FizzBuzz

module Main where

import Control.Monad
import Lib

main :: IO ()
main = forM_ fizzBuzz putStrLn

module Lib
    ( fizzBuzz
    , fizzInt
    ) where

fizzBuzz :: [ String ]
fizzBuzz =
  map fizzInt [1..100]
  where
    fizzInt :: Int -> String
    fizzInt i
      | i `mod` 3 == 0 && i `mod` 5 == 0 = "fizzbuzz"
      | i `mod` 5 == 0 = "buzz"
      | i `mod` 3 == 0 = "fizz"
      | otherwise = show i

FizzBuzz

module Main where

import Control.Monad
import Lib

main :: IO ()
main = forM_ fizzBuzz putStrLn

module Lib
    ( fizzBuzz
    , fizzInt
    ) where

fizzBuzz :: [ String ]
fizzBuzz =
  map fizzInt [1..100]
  
fizzInt :: Int -> String
fizzInt i
  | isMod3 && isMod5 = "fizzbuzz"
  | isMod5 = "buzz"
  | isMod3 = "fizz"
  | otherwise = show i
  where
    isMod3 :: Bool
    isMod3 = i `mod` 3 == 0
    
    isMod5 :: Bool
    isMod5 = i `mod` 5 == 0

Lambda Functions

• Anonymous functions
• Can be written inline
• Like other functions can be assigned to a name

addInt :: Int -> Int -> Int
addInt x y = x + y             -- addInt 1 2 == 3

lambdaAdd :: Int -> Int -> Int
lambdaAdd = \x y -> x + y      -- lambdaAdd 1 2 == 3

map (\i -> i + 1) [1..4]       -- [2, 3, 4, 5]
map (+1) [1..4]                -- [2, 3, 4, 5]

Types and Type Classes

Built in Types

• Int, Integer
• Float, Double
• Char
• Bool
• String == [Char]

Creating Your Own Types

• type - for creating an alias
• data - for creating a new type

type (alias)

type String = [ Char ]

type PeoplesNames = [ String ]

type Person = ( String, String, Int )

data

data Bool = True | False

data WeekDays = Monday | Tuesday | Wednesday | Thursday | Friday


data Person = Person String String Int

data Worker = Employee String String Int | Manager String String Int

getFirstName (Employee firstName _ _) = firstName

data Employee = Employee { getFirstName :: String
                         , getLastName :: String
                         , getAge :: Int
                         }

emp = Employee "Jonny" "Jon" 40

getFirstName emp        -- "Jonny"

Type Parameters

data Maybe a = Just a | Nothing

data [a] = a : [a] | []
data List a = Cons a (List a) | Empty

Type Parameters

data Maybe a = Just a | Nothing


a = Just "hello"   -- Maybe String

b = Just 5         -- Maybe Int

c = Nothing        -- Maybe a

Type Classes

• Like interfaces
• Allow us to keep functionality and data separate
• Useful for polymorphism

myFunc :: (Num a) => a -> a -> a
myFunc x y = x + y

Common Type Classes

• Eq = can they be compared equal
• Ord = can they be compared > or < etc
• Show = can  it be turned into a String
• Read = can it be converted from a String
• Enum = can it be enumerated
• Bounded = does it have a min and max
• Num = is it a number
• Intergral = is it a whole number
• Floating = is it a real number

The Num Type Class

class Num a where
  (+) :: a -> a -> a
  (-) :: a -> a -> a
  (*) :: a -> a -> a
  negate :: a -> a
  abs :: a -> a
{-*SNIP*-}

The Eq Type Class

class Eq a where  
    (==) :: a -> a -> Bool  
    (/=) :: a -> a -> Bool  
    x == y = not (x /= y)  
    x /= y = not (x == y) 

data TrafficLight = Red | Yellow | Green 

instance Eq TrafficLight where  
    Red == Red = True  
    Green == Green = True  
    Yellow == Yellow = True  
    _ == _ = False  

The Eq Type Class

areEq :: (Eq a) => a -> a-> Bool
areEq first second = first == second

Deriving Type Classes

When creating a type, if its composed of types that already implement a Type Class, you can then just derive that Type Class for your new type.

data Employee = Employee { getFirstName :: String
                         , getLastName :: String
                         , getAge :: Int
                         } deriving ( Show, Eq )

Lists

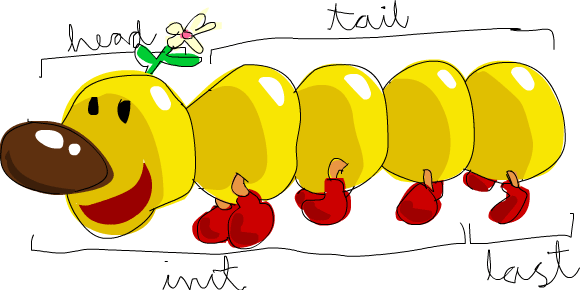
Lists

• Singly linked list
• Can be infinite
• Can be used like an array but be careful

data List a = a :    [a]      | []
data List a = Cons a (List a) | EmptyList

[1, 2, 3, 4, 5]

1 : 2 : 3 : 4 : 5 : []

Cons 1 (Cons 2 (Cons 3 ( Cons 4 (Cons 5 EmtpyList))))

Infinite Lists

• Possible due to Haskell being lazy
• Only computed up to what is used
• Can get stuck in an 'infinite loop'

infinteList = [1..]

oddInfiniteList = [1,3..]

finiteList = take 10 infiniteList

otherFiniteList = (take 10) . (drop 5) oddInfiniteList

Map

• Like a foreach that applies a function to each value
• Don't care how it works, just do it

list = [1, 2, 3, 4]



newList = map (+1) list

int arr[] = {1, 2, 3, 4};
int newArr[] = {0, 0, 0, 0};
int size = 4;
  
for(int i = 0; i < size; i++) {
    newArr[i] = arr[i] + 1;
}

Filter

• Like a foreach that only adds a value if a condition is true
• Don't care how it works, just do it

list = [1, 2, 3, 4]


newList = filter (<3) list

vector<int> arr = {1, 2, 3, 4};
vector<int> newArr;
  
for(int i = 0; i < arr.size; i++) {
    if(arr[i] < 3) {
        newArr.push(arr[i]);
    }
}

List Comprehension

myList = [x     | x <- [1..10] ]        --[1,2,3,4,5,6,7,8,9,10]

myList = [x + 1 | x <- [1..10] ]        --[2,3,4,5,6,7,8,9,10,11]

myList = [x     | x <- [1..10], x < 3]  --[1,2]

myList = [x + 1 | x <- [1..10], x < 3]  --[2,3]

Functor, Applicative, and Monads

Functor

class Functor f where
  fmap :: (a -> b) -> f a -> f b

Apply a function to a computational context

Common Functors

• Maybe
• []
• IO

Functor

myFunc :: Int -> Bool

mayExistInt :: Maybe Int

-- How do I use myFunc with mayExistInt?

result = fmap myFunc mayExistInt
result = myFunc <$> mayExistInt

-- which will result in
result :: Maybe Bool

Why do we care?

Ok, what about multiple params?

Applicative

class Functor f => Applicative f where
  pure :: a -> f a
  (<*>) :: f (a -> b) -> f a -> f b

Apply a function in a context to a context

Common Applicatives

• Maybe
• []
• IO

Applicative

myFunc :: Int -> String -> Bool

mayExistInt :: Maybe Int

mayExistString :: Maybe String

-- How do I use myFunc with mayExistInt and mayExistString?

result = fmap myFunc mayExistInt <*> mayExistString
result = myFunc <$> mayExistInt <*> mayExistString

-- which will result in
result :: Maybe Bool

Why do we care?

Monads

What if I have a value in a context but the function takes a normal value and return a value in a context?

class Applicative m => Monad m where
  (>>=) :: m a -> (a -> m b) -> m b
  return :: a -> m a

  -- Applicative
  pure :: a -> m a

Monads

What do you think the following program does?

module Main where

main :: IO ()
main = do
  hello <- return "hello"
  world <- return "world"
  print (hello ++ world)

Common Monads

• Maybe
• []
• IO

Monads

myFunc :: Int -> Maybe Bool

mayExistInt :: Maybe Int

-- How do I use myFunc with mayExistInt?

result = mayExistInt >>= myFunc

result = do
            i <- mayExistInt
            myFunc i 

-- which will result in
result :: Maybe Bool

Why do we care?

Monads

instance Monad Maybe where
  (>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
  (>>=)    (Just a)   f              = f a
  (>>=)    Nothing    _              = Nothing
  

mayExistInt >>= myFunc

-- if mayExistInt == Nothing :
Nothing

-- if mayExistInt == Just x then f == myFunc and a == x :
myFunc x :: Maybe Bool

Whats happening behind the Maybe >>= curtain?

Monads

getLine  :: IO String -- from the prelude
myFunc   :: String -> IO Bool
myFunc2  :: Bool   -> IO String
putStrLn :: String -> IO () -- from the prelude

result = do inputString <- getLine
            myBool <- myFunc inputString
            computeString <- myFunc2 myBool
            putStrLn computeString 

-- which will result in
result :: IO () --and the appropriate IO actions

Why do we care?

Monad Transformers

Monad Transformers

• This is one way we get "real" programs
• Instead of nesting we stack them like legos
• Then we just require something has the ability to do a context not the context itself
• i.e. requiring MonadIO instead of IO

Tools

GHC/GHCI

• Compiler (GHC)
• REPL (GHCI)
  • Read
  • Eval
  • Print
  • Loop

stack

• www.haskellstack.org
• build tool
• package manager
• project manager
• Setup a new project
  • stack new my-project
  • cd my-project
  • stack setup
  • stack build
  • stack exec my-project-exe

Searching for libs/functions

• https://www.haskell.org/hoogle/
  • Generic search
  • Can search by function parameters
• https://www.stackage.org/snapshots
  • Pick a stack snapshot
  • Search just like you would for Hoogle