Our automated future of mobility

Challenges in prediction and control

Sebastian Hörl

Kyko 2018

Magdeburg, 26 May 2018

The "street" in 1900

The "street" today

Rochester, NY ...

... 1950 ...

... and today

The street of tomorrow?

Autonomous Mobility
Mobility as a Service
Mobility on Demand
Electrification
Aerial Mobility

The street of tomorrow?

Autonomous Mobility
Mobility as a Service
Mobility on Demand
Electrification
Aerial Mobility

How do we predict the impacts?

How do we control the system?

The impact of control?

User optimum vs. system optimum

20 min

5 min

Braess' Paradoxon

User optimum vs. system optimum

20 min

5 min

Braess' Paradoxon

User optimum vs. system optimum

16 min

7 min

9 min

Braess' Paradoxon

User optimum vs. system optimum

16 min

7 min

9 min

Braess' Paradoxon

+ x EUR ?

Signal control

Flow Maximization

Flow Imbalance

Waiting times

Dedicated bus lanes

Signal control

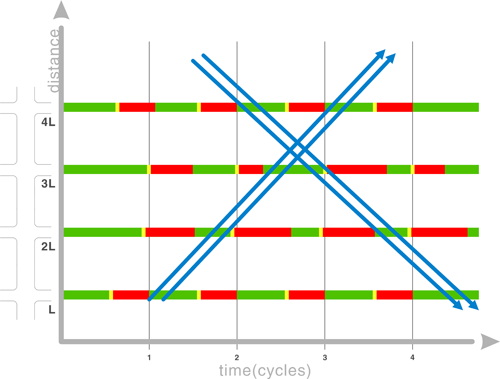
"Green waves"

Scheduling

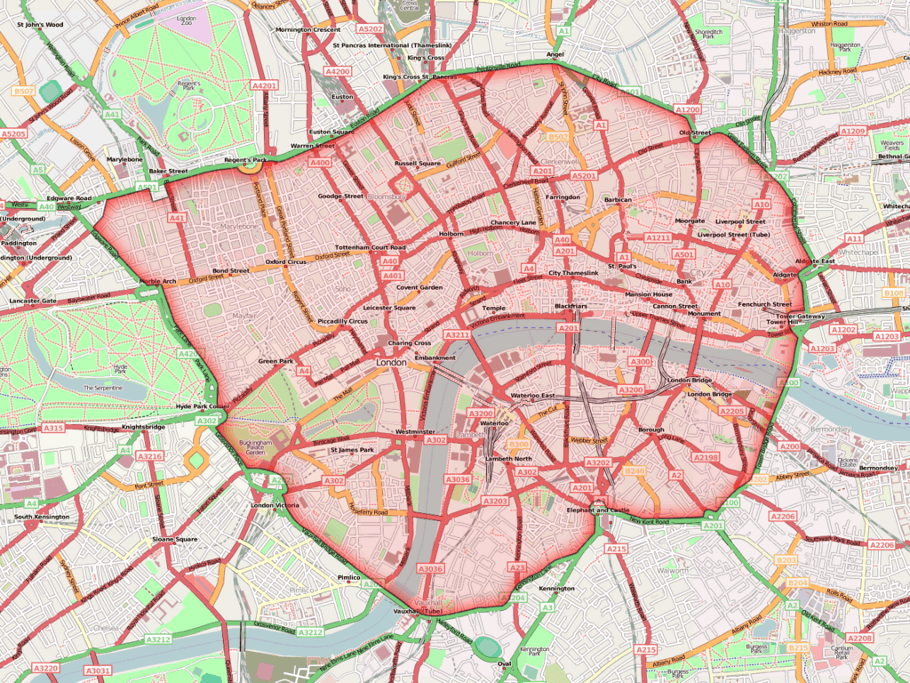
Mobility pricing: London

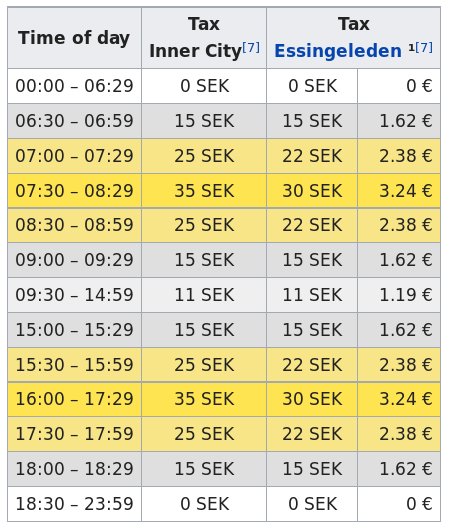
Mobility pricing: Stockholm

Problem: Real-world experiments

Solution: Simulations

MATSim

Home

Work

Shop

Home

until 8am

9am to 6pm

6:15m to 6:30pm

from 6:45pm

walk

public

transport

walk

MATSim

Network simulation

Scoring of the plans

Selection and modification

Scenario

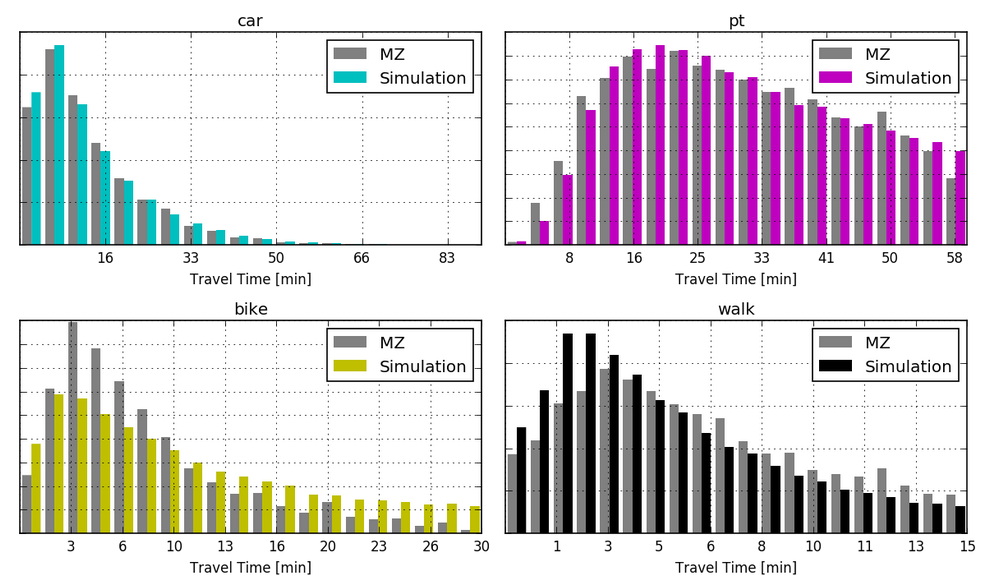
Scenario calibration

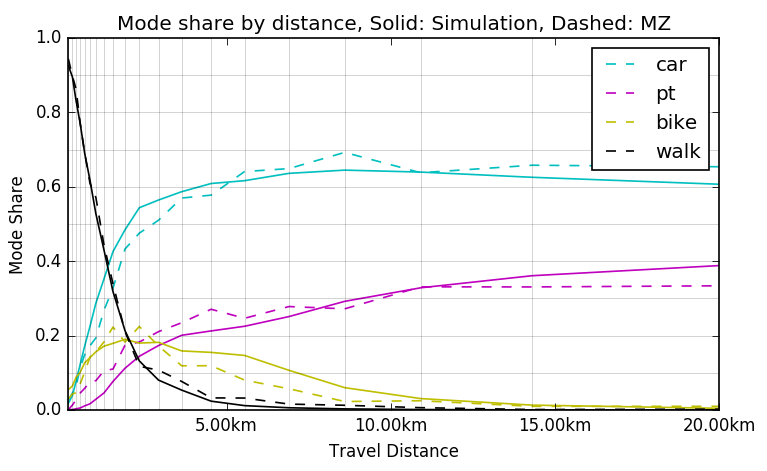
Current research at IVT
Self-driving vehicles

Self-driving vehicles

Access to Mobility

Effective Capacities

Costs

Individualization

Empty distance

Travels

Net effect?

Self-driving vehicles

A_i = \sum_j o_j \cdot f(c_{ij})

Current research

Cost calculator

Model choice model

Simulation (MATSim)
- Scenario
- New components, integration

Cost Calculator

Fleets of autonomous vehicles
Private autonomous vehicles
Comparison with conventional vehicles

Cost Calculator

0.67 CHF

per passenger kilometer

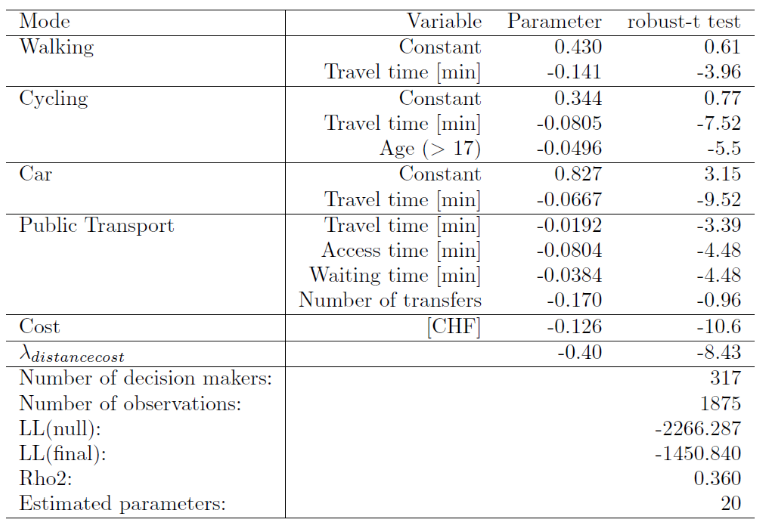
Mode Choice Model

Stated preference survey
- 400 respondents
Attitudes towards different AV services
- Shared AV
- Pooled AV
- AV feed for public transport
Work done by Felix Becker

Mode Choice Model

P(m) = \frac{\exp(V_m)}{\sum_{m'} \exp(V_{m'})}

Simulation of AVs

AV taxi services
Simple dispatching heuristic
(Bischoff & Maciejewski)
Multiple operators
Dynamic demand responses

Idle

Pickup

Drive

Dropoff

Drive

Case study: dispatching strategies

Maximum demand case
Freeflow conditions
Four dispatching strategies
- Load-balancing heuristic
- Global Eucledian Bipartite Matching
- Feedforward Fluidic Rebalancing
- daptive Uniform Rebalancing