Quantifying risk for nuclear components constructed with known manufacturing tolerances
Tritium production is of critical importance to prospective DT fusion power plants.
Tritium is not found in sufficient quantities on Earth and therefore fusion power plants will have to be self sufficient.
for every D+T Fusion reaction the breeder blankets must produce at least 1.1 tritium atoms to account for losses in the system.
The requirement for tritium
Importance of simulating tritium production accurately
Under estimating the tritium production could result excessive storage requirements. Due to the diffusivity of tritium this could also result in challenges for monitoring the tritium inventory and keeping within the tritium release limits.
Mature blanket designs such as the HCLL and HCPB achieve Tritium Breeding Ratio (TBR) values around 1.2 to 1.3 .
Tritium consumption for a 3GW (thermal) power plant is approximately 200g. Over estimating the tritium production by 1% could lead to fuel shortage of 2g per day ($60,000 per day).
Uncertainties currently considered
Research has previously been carried out on the topic of uncertainties in tritium production.
- Uncertainty due to nuclear data [1]
- Uncertainties due to material changes during irradiation [2]
- Uncertainties due to over simplification of geometry [3]
[1] F. Thomas et al, Quantifying TBR uncertainty due to lead nuclear data in HCLL blanket modelling by the Total Monte-Carlo, Fusion Engineering and Design, 2017
[2] J.Shimwell et al, Spatially and temporally varying tritium generation in solid-type breeder blankets, Fusion Engineering and Design, 2015, http://dx.doi.org/10.1016/j.fusengdes.2015.04.018
[3]L. El-Guebaly et al, Toward the. Ultimate Goal of Tritium Self-Sufficiency, Fusion Engineering and Design, 2009, http://dx.doi.org/10.1016/j.fusengdes.2008.12.098
Aims of the pilot project
Quantifying the uncertainty arising from variation in the physical dimensions of breeder blanket components will allow designers to specify acceptable tolerances to future manufacturers.
This proposal seeks to establish a relationship between manufacturing tolerances and uncertainty in tritium production.
Research plan
Generate models with geometry variation
Simulate tritium production response
Generate manufacturing tolerance distributions
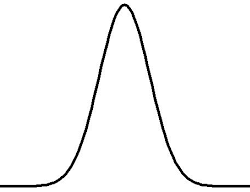
tolerance (mm)
Probability
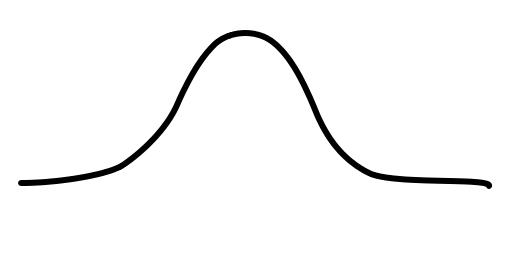
tolerance (mm)
Probability
Find risk associated with tolerances and make a recommendation for acceptable tolerance distributions.
Mean =10mm, v1=11mm, v2=8mm, v3=12mm ... tritium production = 1.001
Mean =10mm, v1=13mm, v2=9mm, v3=11mm ... tritium production = 1.004
Research plan
Generate 3D CAD models of tritium breeder blankets with geometry that represents a range of different manufacturing tolerances.
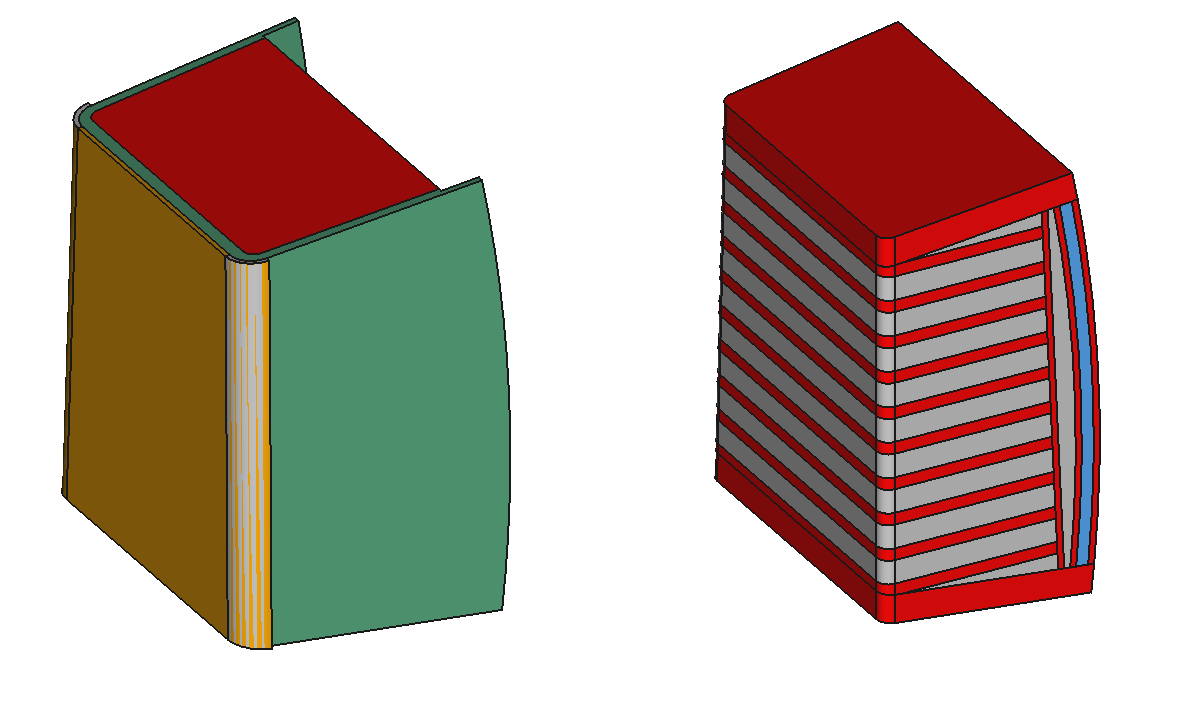
*diagram shows simplified geometry, models generated will contain more dividing plates


Research plan
Simulate tritium production
This involves converting the CAD to geometry suitable for neutronics modelling.
Options include:
Constructive Solid Geometry and MCNP
Constructive Solid Geometry and Serpent
Unstructured mesh geometry and MCNP
Surface mesh geometry (STL) and Serpent



Research plan
Quantifying the uncertainty arising from variation in the physical dimensions of breeder blanket components will allow designers to specify acceptable tolerances to future manufacturers.
The simulation input parameters along with the simulation results are used as the inputs for uncertainty quantification.
Variance
param1
param2
...
Tritium
1
11
9.5
...
1.001
1
12
9
...
1.002
1.5
13
8
...
1.003
1.5
14
10
...
1.009
Expectations
*diagram shows simplified geometry without the first wall and rear components

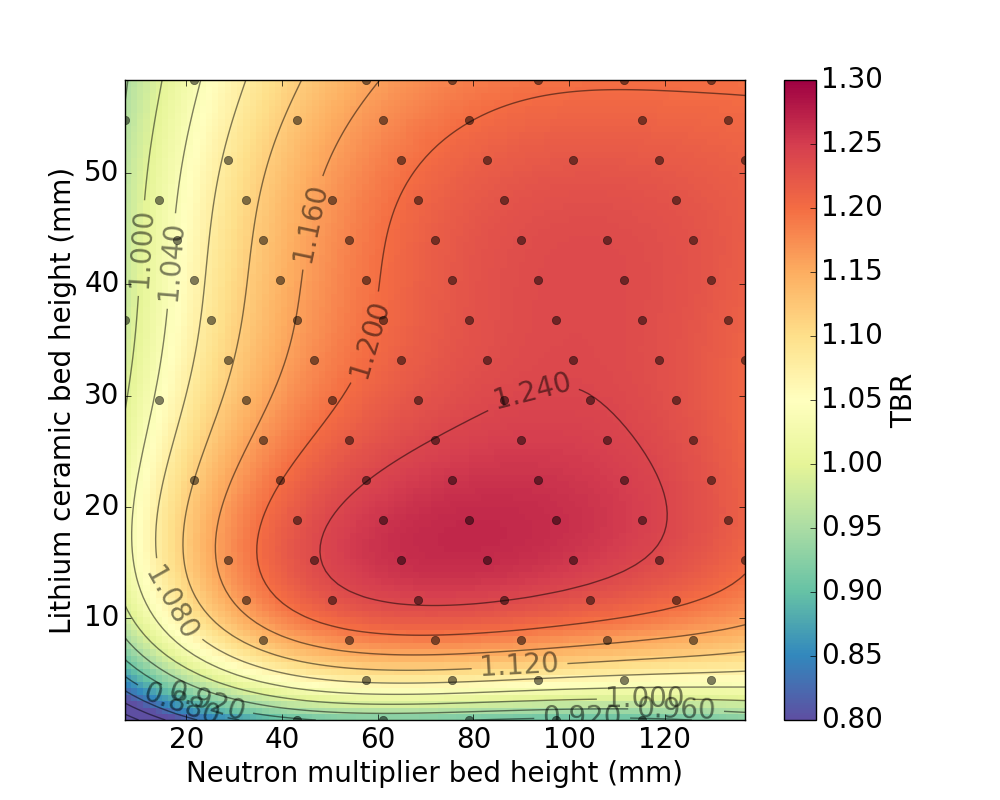
There is an optimal ratio of lithium ceramic to neutron multiplier.
Variation of the cooling plates' dimensions will change the volume available for pebble beds and make it difficult to ensure the optimal ratio is maintained.
The current HCPB design for a lithium bed is 11.6mm in height. Variation in the bed height will have an effect on TBR and the volumetric heating.
Length along contour line
Constant TBR
High Risk
Result
Lower Risk
TBR
A more informed choice can be made when selecting designs.
Design points with equal performance lie on the same performance contour line but differ in terms of associated uncertainty / risk.
Risk
Quantifying risk
By Jonathan Shimwell
Quantifying risk
- 463


