Agenda
Overview
Technical Details
Our Team



Overview


Simple task
Nuclei segmentation
Overview












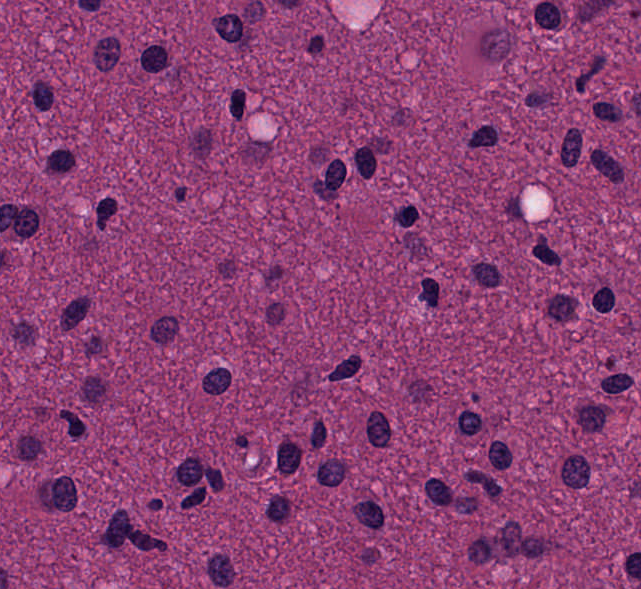



















Train
Test
Input images sample variability
Overview



Differing Saliency
- some nucleus can be easily seen
- some are barely distinguishable
- some have homogenous structure
- some have nucleous in the center
Overview


Varying shape and size
- some are elliptical
- some are oblong
- some are large
- some are very small


Overview



Varying level of nuclei attachment
- some images are very dense
- some are sparse
- some have large groups of glued nuclei
Pipeline
Input image
Preprocessing
Morphological pooling
Watershed ensemble generation
Thresholding
Morphological ensemble generation
Technical Details
Watershed pooling
Segmented mask
Preprocessing


Hematoxylin


Eosin
Background
Technical Details
Color deconvolution
Pipeline
Preprocessing


Hematoxylin


Eosin
Background

Hematoxylin Channel Extraction
Technical Details
Color deconvolution
Pipeline
Preprocessing
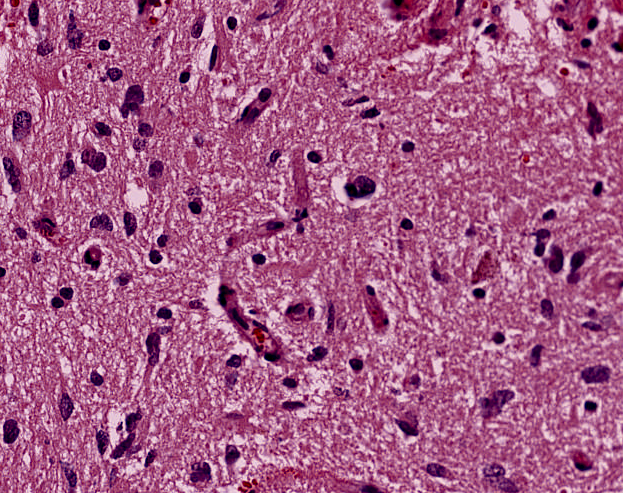
Reinhard's Color Normalization
References:
- Reinhard, E., Adhikhmin, M., Gooch, B., Shirley, P.: Color transfer between images. IEEE Computer Graphics and Applications 21(5) (2001) 34–41
- Wang, Y., nd L. Wu, S.C., Tsai, S., Sun, Y.: A color-based approach for automated segmentation in tumor tissue classification. In: Proc. Conf. of the IEEE Engineering in Medicine and Biology Society. (2007) 6577–6580

Target image
Technical Details

Pipeline
Preprocessing

Hematoxylin Channel Extraction



Reinhard's Color Normalization
Target image
Technical Details
Pipeline
Thresholding


Possible algorithms:
- K-means clustering
-
Fuzzy c-means clustering
-
Gaussian mixture models
2. With spatial information
1. No spatial information
- Spatial information Fuzzy c-means clustering
-
Fast spatial distance weighted Fuzzy c-means clustering
-
Dictionary model
References:
- Zeng, Huang, Kang and Sang. Image segmentation using spectral clustering of Gaussian mixture models. Neurocomputing 144:346–356, 2014.
- Guo, Liu, Wu, Hong and Zhang. A New Spatial Fuzzy C-Means for Spatial Clustering. WSEAS Transactions on Computers 14:369-381, 2015.
- Dahl and Larsen. Learning Dictionaries of Discriminative Image Patches. In: Proc. British Machine Vision Conference. p.77, 2011.
- Hamed Shamsi and Hadi Seyedarabi, Member, IACSITA Modified Fuzzy C-Means Clustering with Spatial Information for Image Segmentation,International Journal of Computer Theory and Engineering, Vol. 4, No. 5, 2012.
Technical Details
Pipeline
Thresholding
K-means clustering
Parameters:
- number of color clusters
- number of most most intensive clusters to be classified as nuclei
Models
- k-means(3,1)
- k-means(4,2)
- k-means(6,3)






input
color clusters
1
6
5
4
3
2
Technical Details
Pipeline

Thresholding







input
color clusters
top 3
most intensive clusters sum
1
6
5
4
3
2
4+5+6
K-means clustering
Parameters:
- number of color clusters
- number of most most intensive clusters to be classified as nuclei
Models
- k-means(3,1)
- k-means(4,2)
- k-means(6,3)
Technical Details
Pipeline

Thresholding
Gaussian Mixture Model
Parameters:
- number of color clusters
- number of most most intensive clusters to be classified as nuclei
- which of the distribution parameters (means, covariances,weights) should be updated
- which covariance option (diagonal,full,tied,spherical) should be used
Models
- GMM(3,1,{means,covariances},diagonal)
- GMM(6,3,{covariances},diagonal)
- GMM(6,3,{covariances},tied)
References:
- Zeng, Huang, Kang and Sang. Image segmentation using spectral clustering of Gaussian mixture models. Neurocomputing 144:346–356, 2014.
Technical Details
Pipeline
Thresholding
Spatial distance weighted fuzzy c-means clustering
Parameters:
- number of color clusters
- number of most most intensive clusters to be classified as nuclei
- fuzziness parameter
- spatial information importance
- number of neighbours
Models
- SDWFCM(3,1,2,0.9,8)
- SDWFCM(3,1,2,0.9,24)
- SDWFCM(3,2,2,0.9,24)
cluster center
spatial distance weighted funcion
weighted distance
membership probabilty
objective function
References:
- Hamed Shamsi and Hadi Seyedarabi, Member, IACSITA Modified Fuzzy C-Means Clustering with Spatial Information for Image Segmentation,International Journal of Computer Theory and Engineering, Vol. 4, No. 5, 2012.
Technical Details
Pipeline
Thresholding
Dictionary model
References:
- Dahl and Larsen. Learning Dictionaries of Discriminative Image Patches. In: Proc. British Machine Vision Conference. p.77, 2011.
Technical Details
Learning:
- seeding dictionaries of texture and label patches
- iterative clustering of patches according to label similarity
Segmentation:
- assigning the idealized label of the most similar cluster centroid


Pipeline
Thresholding
Parameters:
- patch size
- label similarity threshold
- percentage of seeding and for training
- number of training iterations
- adjustment coefficient for centroids of texture clusters
Models
- DM(1,0.4,0.01,0.1,5,0.05,0.5)
- DM(1,0.5,0.01,0.1,20,0.05,0.0)
- DM(2,0.6,0.01,0.1,5,0.05,0.0)
- DM(3,0.6,0.01,0.1,5,0.15,0.5)
References:
- Dahl and Larsen. Learning Dictionaries of Discriminative Image Patches. In: Proc. British Machine Vision Conference. p.77, 2011.
Technical Details
Dictionary model
Pipeline
Thresholding



Reality is far from perfect:
- leftover artifacts
- hollow shapes
- glued nuclei groups
Technical Details
Pipeline
Thresholding
Operations:
- dilation and erosion
- reconstruction by erosion
- closing and opening
- fill binary holes
Morphological Transformations
Technical Details


Pipeline
Thresholding
Operations:
- dilation and erosion
- reconstruction by erosion
- closing and opening
- fill binary holes
Morphological Transformations
Problems:
- Sample diversity
- Diversity within one image
- "one size fits all" structuring element does not exist
Technical Details


Pipeline


Morphological ensemble generation








k-means(3,1)
k-means(4,2)
SDWFCM(3,2,2,0.9,24)
1
2
r
Morphological ensemble
Technical Details
Pipeline









k-means(3,1)
k-means(4,2)
SDWFCM(3,2,2,0.9,24)
1
2
r

Morphological ensemble
Morphological pooling
probabilty map
Technical Details
Pipeline









k-means(3,1)
k-means(4,2)
SDWFCM(3,2,2,0.9,24)
1
2
r


Morphological ensemble
k-means clustering
Morphological pooling
probabilty map
Technical Details
Pipeline
nuclei detachment
Watershed ensemble generation


Watershed algorithm
- local maxima search space
- minimal distance between markers
- other
Technical Details
Pipeline
nuclei detachment
Watershed ensemble generation


Watershed algorithm
- local maxima search space
- minimal distance between markers
- other
Problems:
- Sample diversity
- Diversity within one image
- "one size fits all" parameter set does not exist
Technical Details
Pipeline
Watershed ensemble generation




watershed realizations
thresholding output
Technical Details
Pipeline
Watershed ensemble generation




watershed realizations



thresholding output
edge realizations
Technical Details
Pipeline
Watershed pooling




probability map
thresholding output

edge realizations
Technical Details
Pipeline
Watershed pooling




probability map
thresholding output

modified thresholding output

overimpose
edge realizations
Technical Details
Pipeline
Watershed pooling




probability map
thresholding output

modified thresholding output

final segmentation mask

watershed
overimpose
edge realizations
Technical Details
Pipeline
Our Team
Grzegorz Żurek
R&D Stermedia
Wroclaw University of Technology




Jakub Czakon
R&D Stermedia
Piotr Giedziun
R&D Stermedia
Ph.D Witold Dyrka
R&D Stermedia
Wroclaw University of Technology

Piotr Krajewski
CIO Stermedia

Michał Błach
R&D Stermedia
Wroclaw University of Technology



MD Łukasz Fuławka
Patomorphology resident
Lower Silesian Oncology Center

Contact us
info@stermedia.pl
jakub.czakon@stermedia.pl
grzegorz.zurek@stermedia.pl
We are looking forward to collaborating with you
Thank you for attention
Segmentation Algorithm
By Stermedia Sp. z o.o.
Segmentation Algorithm
presentation for MICCAI 2015
- 3,454


