Complex Adaptive Systems

Introduction to Computational Models of Social Life

John H. Miller; Scott E. Page

reviewed by Talha Oz

March 2014

Miller

John H. Miller

B.A in economics, B.S. in finance ’82 Colorado
Ph.D. in economics Michigan ’88
Postdoc Santa Fe Institute ’90 (‘03 Research Professor)
Prof. CMU Social & Decision Sciences ’90-’95-’00

Synopsis

Concepts of CAS

emergence, self-organized criticality, automata, networks, diversity, adaptation, and feedback

How CAS can be explored

using methods ranging from mathematics to computational models of adaptive agents

Key tools and ideas that have emerged in the CAS field since the mid-1990s

introduction

Complexity. Interactions of components
Adaptivity. Intelligence of components
CAS. So many such components

Back. Adam Smith in the Wealth of Nations (1776)
Last decade. Tools & techniques => theories

Complexity in Social Worlds

The Standing Ovation Problem

Economics graduate students

si(q) = q + εi if T1< si(q) then stand up
if α>T2 then everyone stands up.

Friendship, location

Heterogeneity & Feedback vs Averaging

Negative. Bees huddling and fanning. Stability thanks to genetic diversity. (Demo)
Positive. Attack of the killer bees. Varying response threshold [1,100]

Tiebout Model (chili demo)

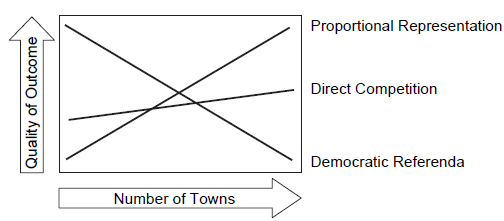
Issue-by-issue
Party based

Winning party takes all
Blend by weighted votes

Preliminaries

Models as maps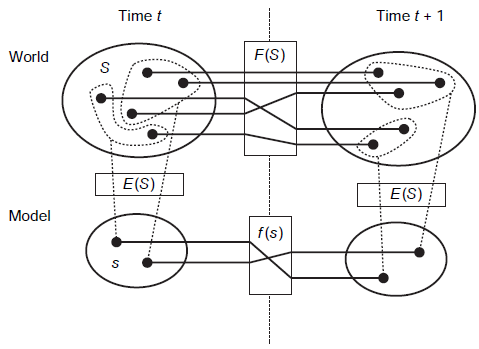

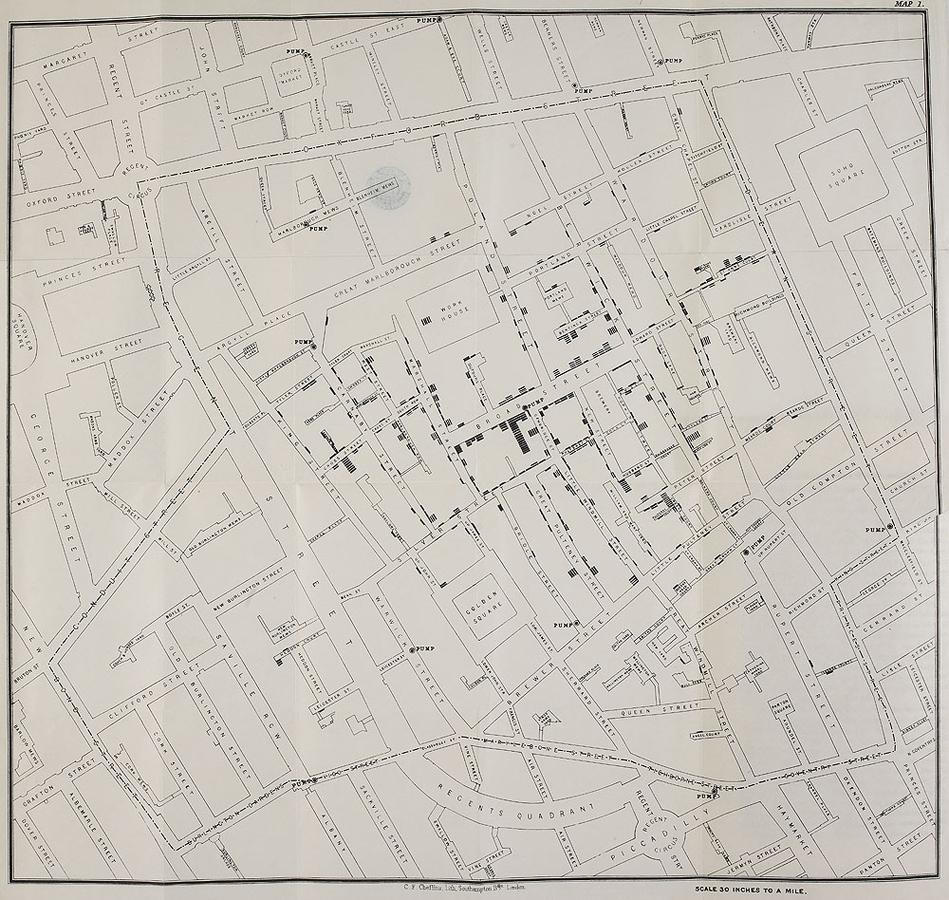
Snow's cholera map

On emergence

Computation as theory

Theoretical tools

detailed verbal descriptions such as Smith's (1776) invisible hand
mathematical analysis like Arrow's (1951) possibility theorem
thought experiments including Hotelling's (1929) railroad line
mathematical models derived from a set of first principles (econ.)
employ different tools for better theories. For supply and demand:

thought experiments using Walrasian auctioneers,
axiomatic derivations of optimal bidding behavior,
computational models of adaptive agents, and
experiments with human subjects.

cont'd

Computation as a theory (theoretical tool)

abstractions maintain a close association with the real-world agents of interest
uncovering the implications of these abstractions requires a sequential set of computations (not computers!) involving these abstractions

Neoclassical economics

individuals optimize their behavior
given mathematical constraints, underlying agents in the real system are subsumed into a single object (a representative agent)
incorporate driving forces (such as system seeks an equilibrium)
computation is used in the models for solving numerical methods

computation as theory - II

Agent-based objects (computation as a theoretical model)

abstractions are not constrained by the limits of mathematics
collection of agents solved by their interactions using computations

Good models vs simulation

simple entities and interactions vs complicated
implications robust to large class of changes vs less robust
surprising results that motivates new predictions vs less surprising
easily communicated to others vs may not be that easy

Objections to Computation as Theory

Q: answers are built in to the model, cannot learn anything new !

all tools build in answers. Clarity is key here. hidden or black-box features are bad
a model is bounded by initial framework but it can allow for new theoretical insights

Q: computational models are brittle !

crashes are not unique to computational models
can be prevented by better designs

Q: computational models are hard to understand !

due to lack of commonly accepted means for communication. UML, ODD.

Cont'd

Q: computations lack discipline !

lack of constraints is indeed a great advantage. Mathematical models become unsolvable when practitioners break away from limited set of assumptions.
a discipline similar to the one required for lab-experiments is being formed: Is the experiment elegant? Are there confounds? Can it be easily reproduced? Is it robust to differences in experimental techniques? Do the reported results hold up to additional scrutiny?
flexibility. mathematical models solved by a set of solution techniques and verification mechanisms. Given the newness of many computational approaches it will take some time to agreed-upon standards for verification and validation

CONT'd

Q: They are only approximations to specific circumstances !

Giving exact answer might not be that important; relying on approximations may be perfectly acceptable in some cases.
Generalizability is tied to the way model created, not the medium. Bad mathematical models may not be extended beyond their initial structure too.

Why Agent-Based Objects?

Flexibility versus Precision

Verbal to mathematical tools

Process Oriented

How agents interact, when, with whom
What information an agent has access to

Adaptive Agents

Rationally bounded. Learning Algorithms

Inherently Dynamic

In natural systems, equilibria = death

Heterogeneous Agents and Asymmetry

Heterogeneity and asymmetry accommodated easily

Scalability

Mathematical models for a few (duopolies) or many (perfect competition) agents

CONT'D

Repeatable and Recoverable

Initial state can be recovered; experiments can be repeated precisely

Constructive (analogy: proof by construction vs proof by contradiction)

Generative approach is a distinct and powerful way to do social science

Low Cost (create. Repeat)
Economic E. coli (E. coni?)

Further Investigation of cas on models

Forest Fire Model, Abbott’s Flatland, Cellular Automata, Social Cellular Automata, Majority Rules, The Edge of Chaos, A Roving Agent, Segregation, The Beach Problem, City Formation, Networks, Self-Organized Criticality and Power Laws, Agent Behavior, Adaptation, A Taxonomy of 2 × 2 Games, Games Theory: One Agent, Many Games, Evolving Communication, The Full Monty, ...