Kalman filter
History
- Named by Rudolf E. Kálmán (*1930 Hungary)
- First described in 1958-1961
- Trajectory estimation for Apollo (NASA)
- Navigation of nuclear ballistic missile submarines (US Navy)
- Navigation systems of cruise missiles
- Navigation systems of modern spacecrafts (Space Shuttle 2011)
- Attitude control and navigation systems of the International Space Station (ISS)
G-H Filter
G-H Filter
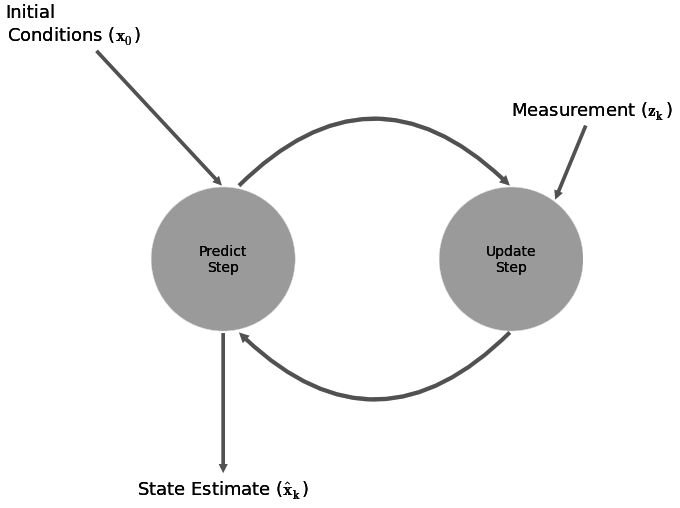
G-H Filter
estimates = [measurement]
predictions = []
for m in measurements:
# prediction step
prediction = prediction + behavior_model*time_step
behavior_model=behavior_model
predictions.append(prediction)
# update step
residual = m - prediction
behavior_model = behavior_model + H * (residual/time_step)
prediction = prediction + G * residual
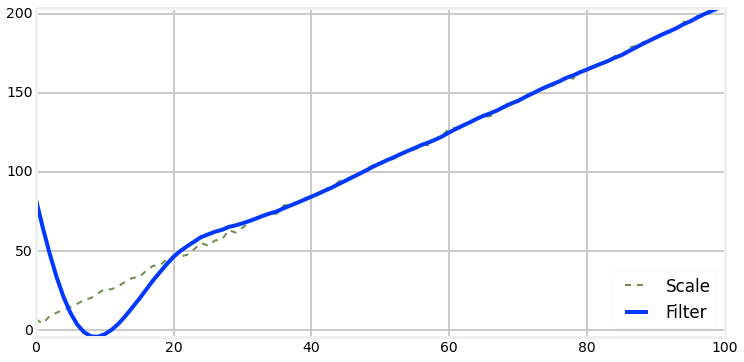
estimates.append(prediction)Bad initial condition
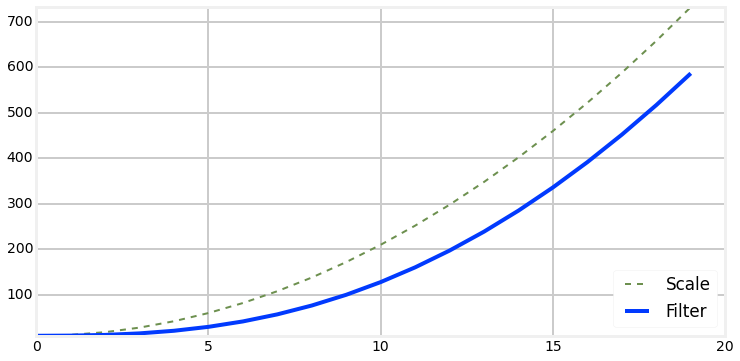
Acceleration
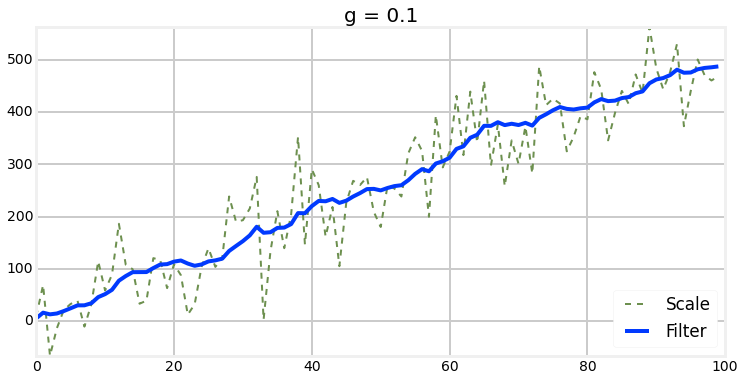
Choosing of G
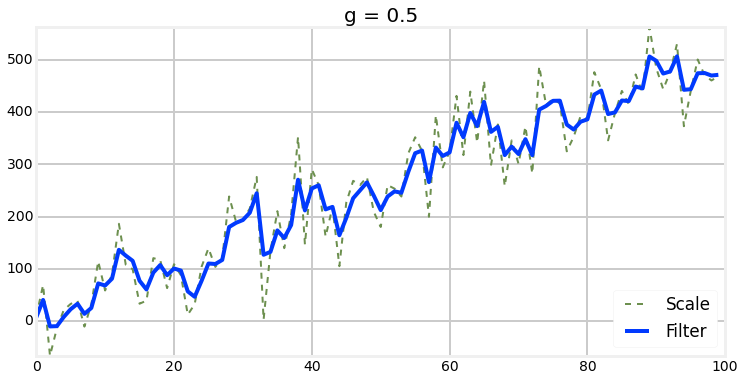
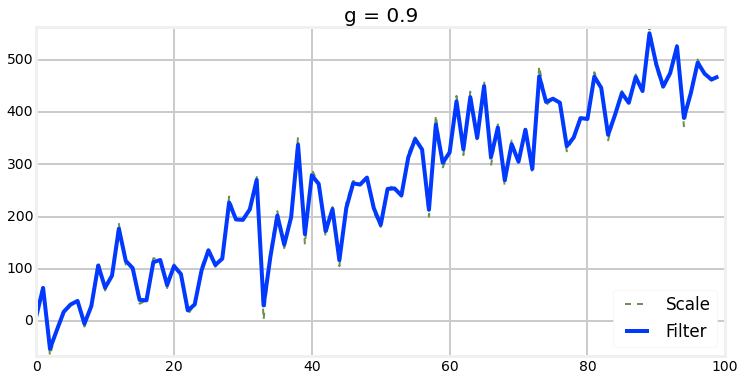
Choosing of H
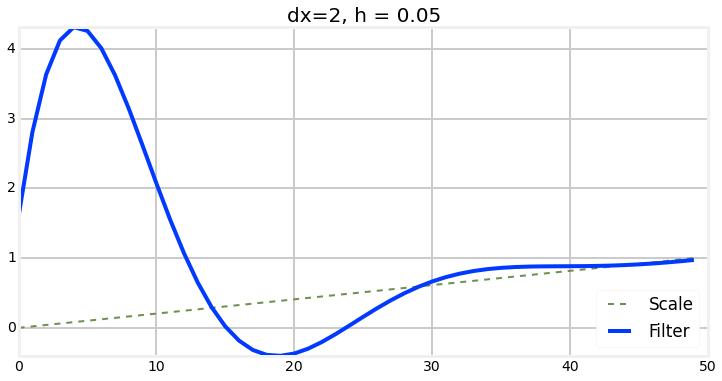
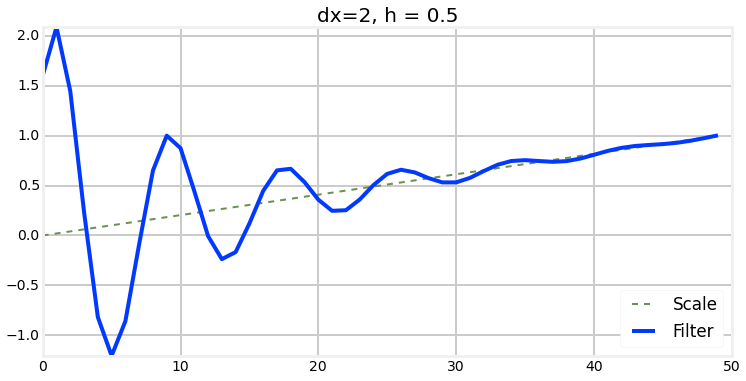
Kalman filter
Main idea
- Assume imperfect sensor measurements.
- We need Object motion model.
- Our measurements contains measurement noise
- Process noise describes imperfect object motion model

Kalman filter
How to describe measurement?
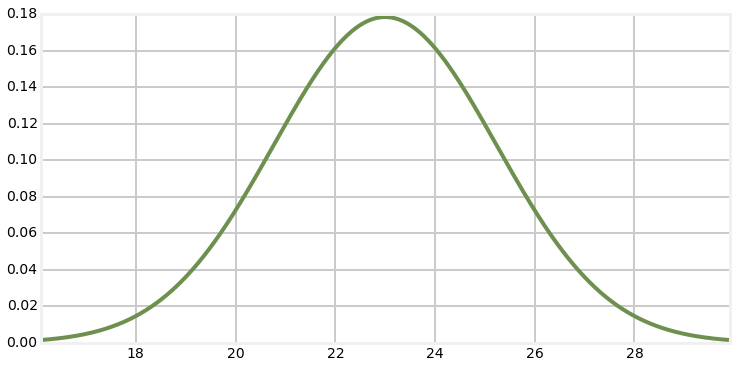
X ~ N
Kalman filter - 1D
Initial conditions
- First expected values can be random
- Describe confidence with big variance
Prediction step
- Sum of gaussians
Kalman filter - 1D
Correction step
- Multiplication of gaussians
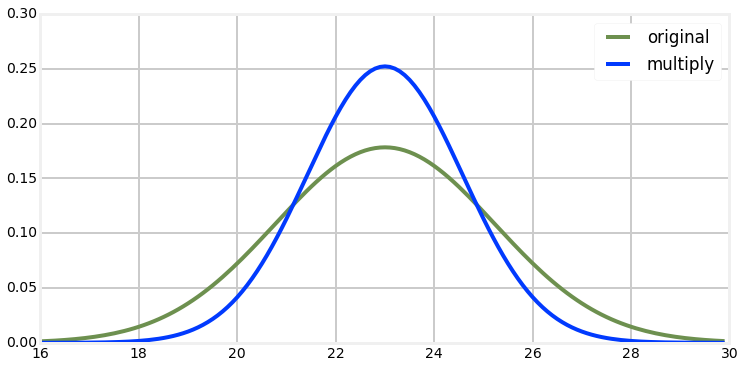
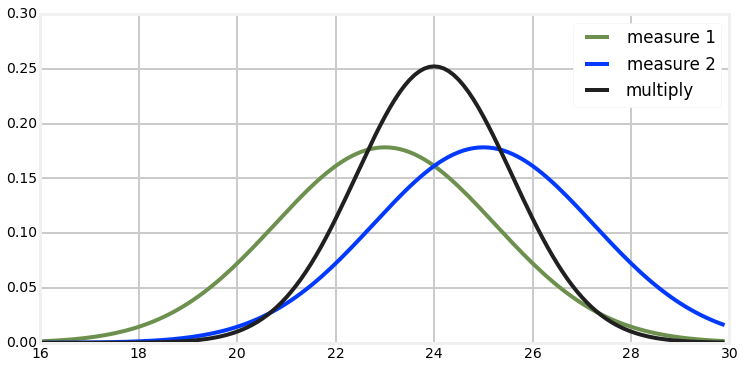
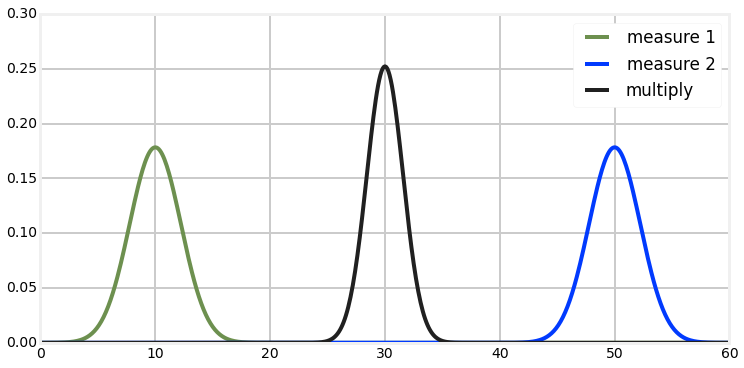
Kalman filter - 1D
Example for understanding
Kalman filter - 1D
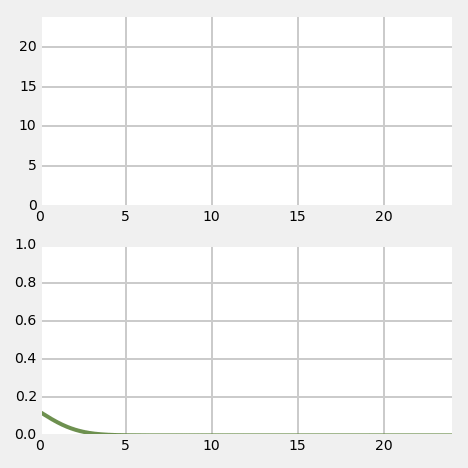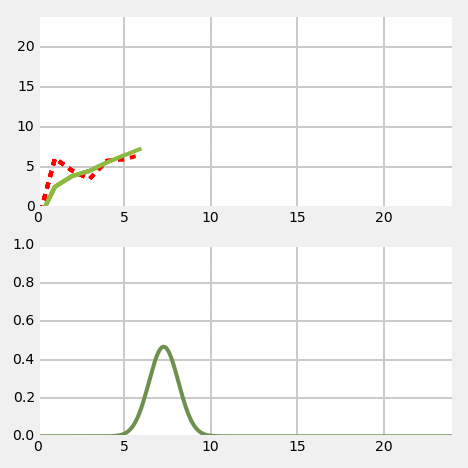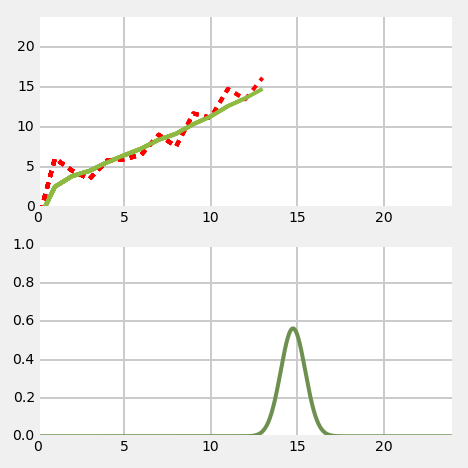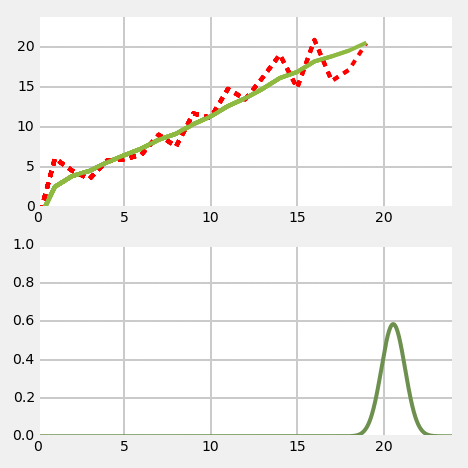
Kalman filter - 1D
Relationship to G-H filter
Kalman filter - 1D

Kalman filter - 1D
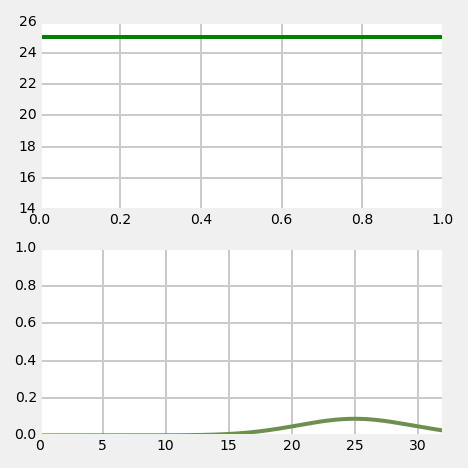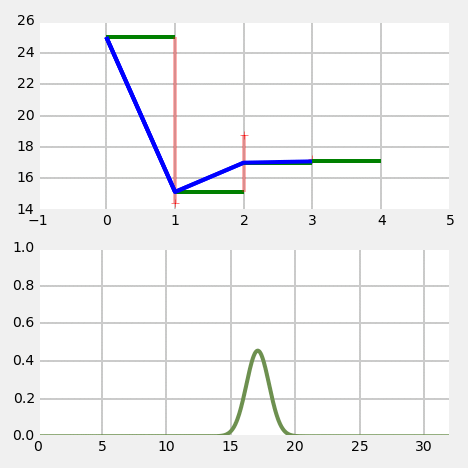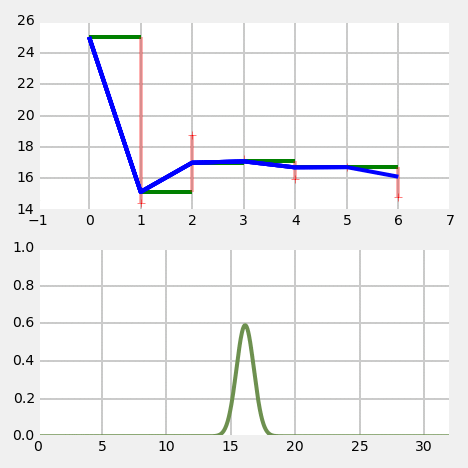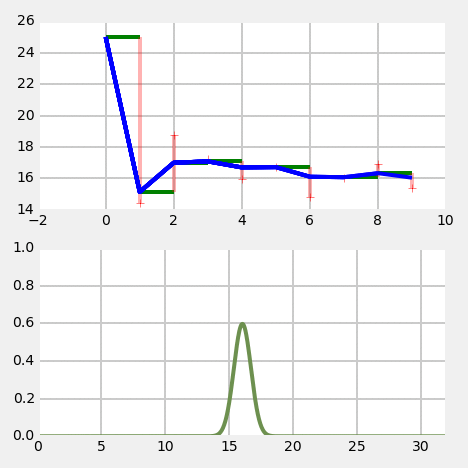
Kalman filter - 1D
Extreme amount of noise
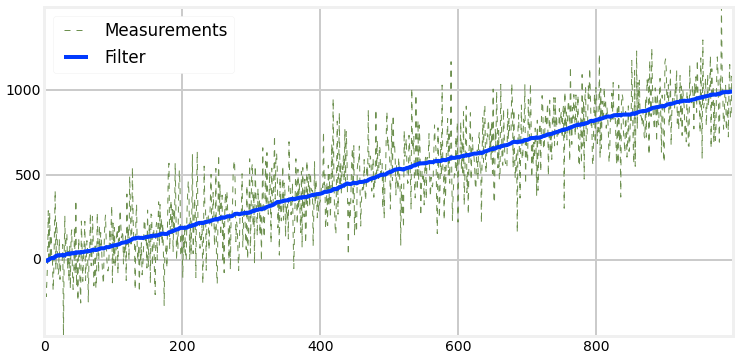
Kalman filter - 1D
Bad Initial Estimate
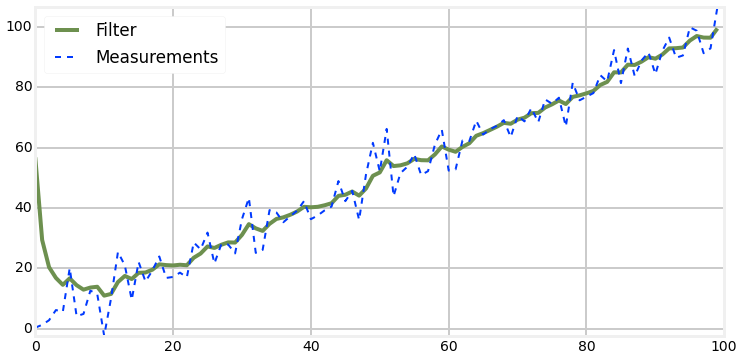
Kalman filter - 1D
Nonlinear Systems
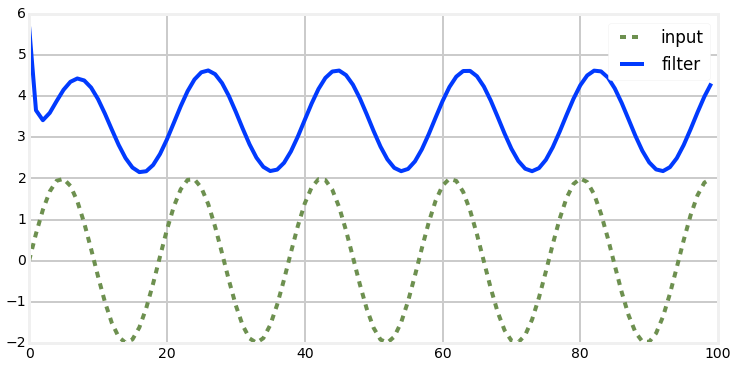
Terrible!
Kalman filter - 1D
Noisy Nonlinear Systems
Terrible!
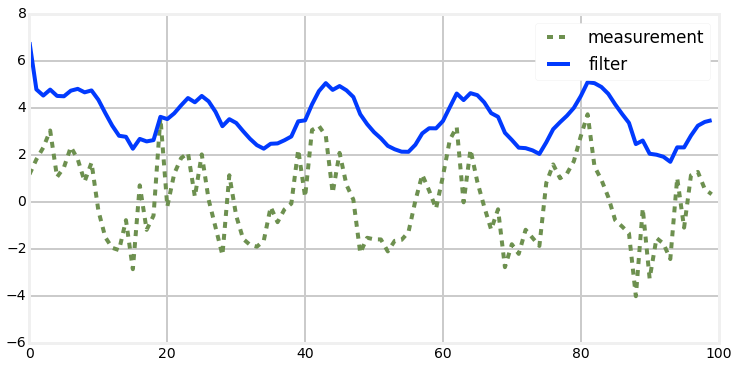
Multivariate Kalman filter
What is different?
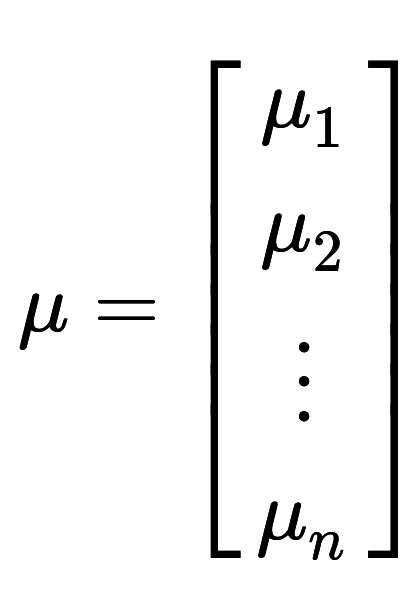
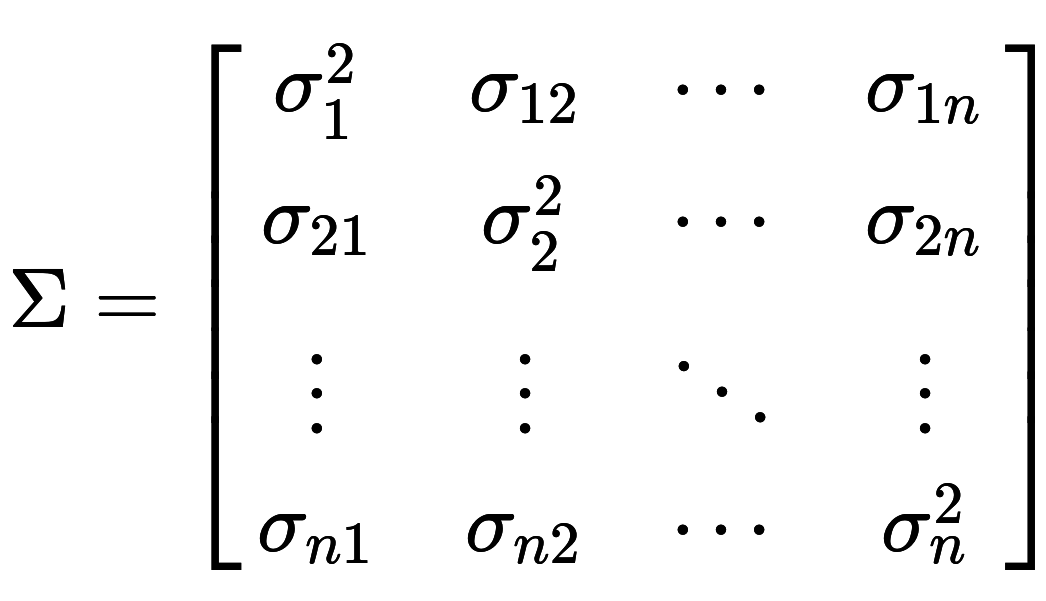
Multivariate Kalman filter
What is different?
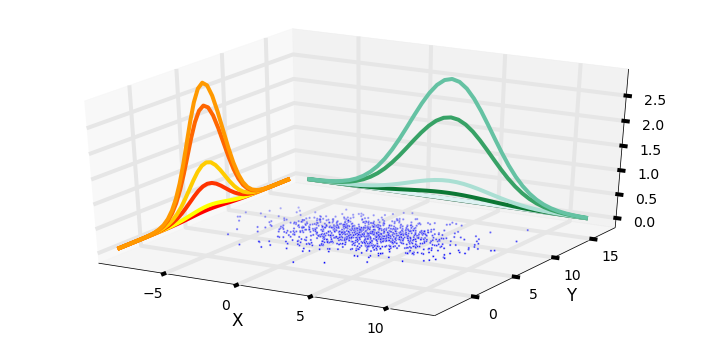
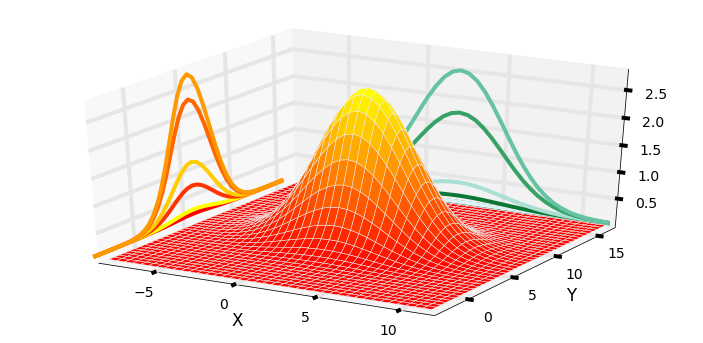
Multivariate Kalman filter
The superposition of the two covariances is where all the magic happens.
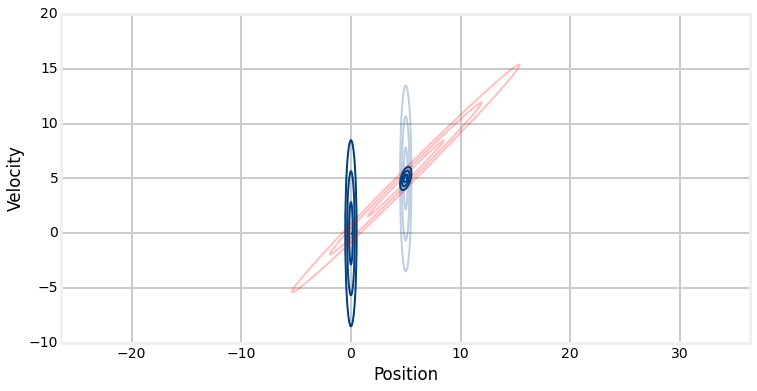
Velocity is unobserved variable
Multivariate Kalman filter
Algorithm
Prediction step
Update step
Legend
-
x - state
-
P - uncertainty covariance
-
Q - process uncertainty
-
u - motion vector
-
B - control transition matrix
-
F - state transition matrix
-
H - measurement function
-
R - state uncertainty
-
S - measurement space
-
K - kalman gain
Multivariate Kalman filter
Algorithm
Prediction step
Update step
Innovation or measurement residual
Innovation (or residual) covariance
Map system uncertainty into optimal kalman gain
Updated (a posteriori) state estimate
Predicted (a priori) state estimate
Predicted (a priori) estimate covariance
Updated (a posteriori) estimate covariance
Multivariate Kalman filter
Algorithm
-
predict the next value for x
-
adjust covariance for x for uncertainty caused by prediction
-
get measurement for x
-
compute residual as: "x - x_prediction"
-
compute kalman gain based on noise levels
-
compute new position as "residual * kalman gain"
-
compute covariance for x to account for additional information the measurement provides
Multivariate Kalman filter
Algorithm
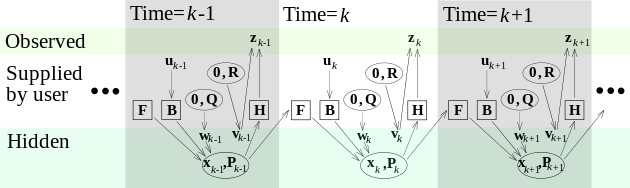
Kalman filter - step by step
1. Initialization
- initialize state x and covariance matrix P
2. Design transition function
- encode object motion model to transition function matrix
- e.g.:
3. Design the Motion Function
- Design control input and state function
- Optional (u = 0)
Kalman filter - step by step
4. Design the Measurement Function
- Design measurement function in matrix form
- Residual need to be from same measurement space, otherwise it's nonsense
5. Design the Measurement Noise Matrix
- The measurement noise matrix models the noise of sensors as a covariance matrix.
- e.g. White noise
6. Design the Process Noise Matrix
- quite demanging, out of scope this presentation
Plots
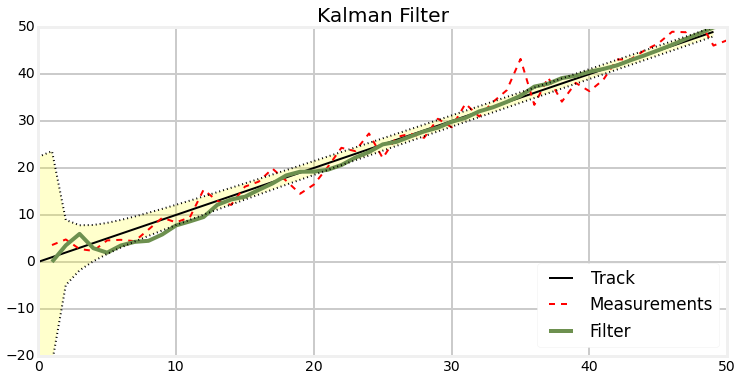
Plots
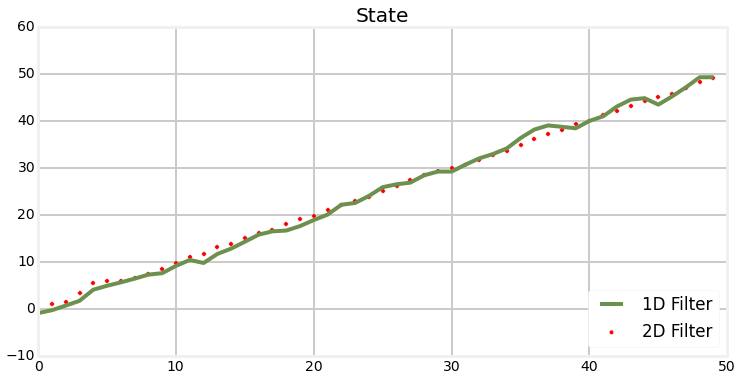
1D vs 2D
Plots
Process noise
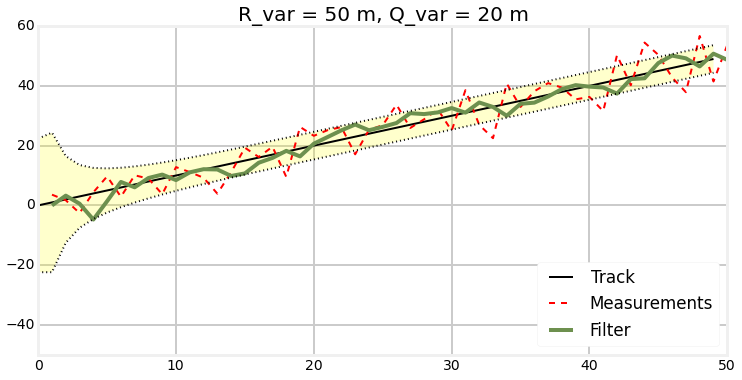
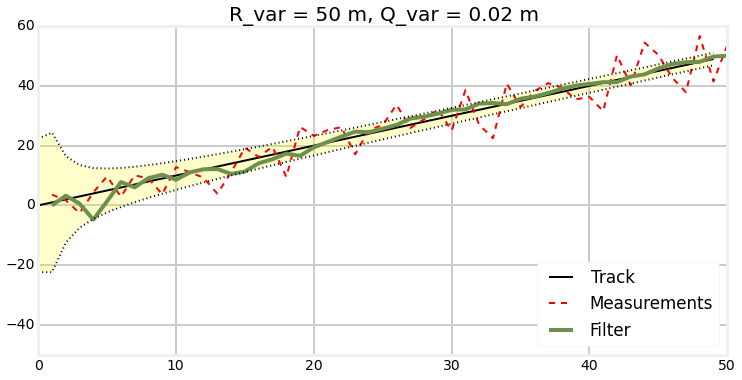
Plots
Measurement noise and bad init
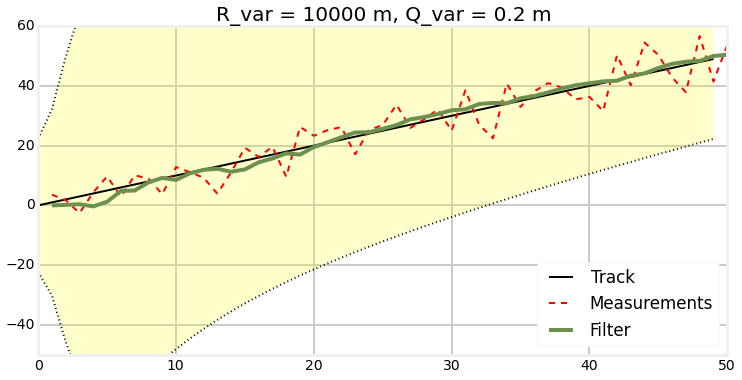
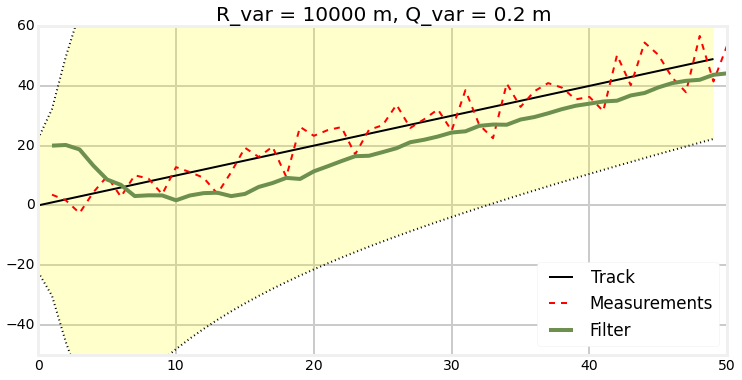
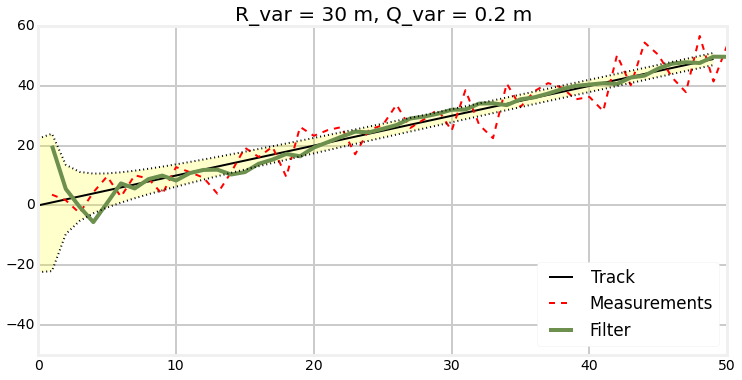
Plots
Progress
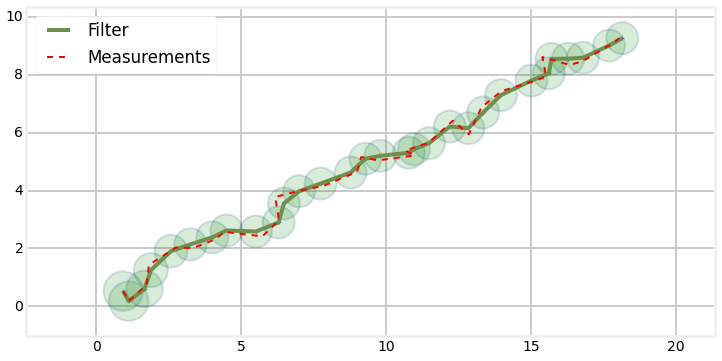
Plots
Animated progress
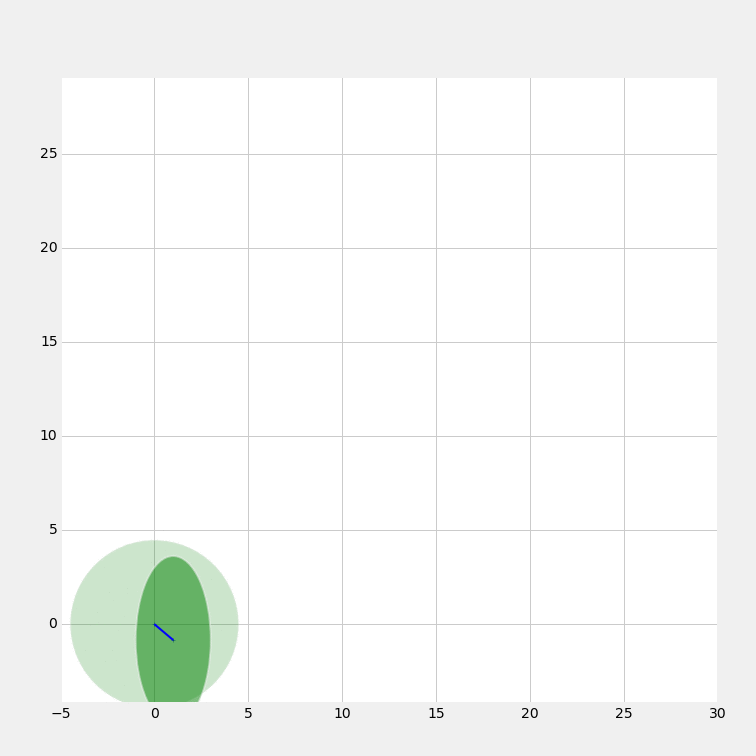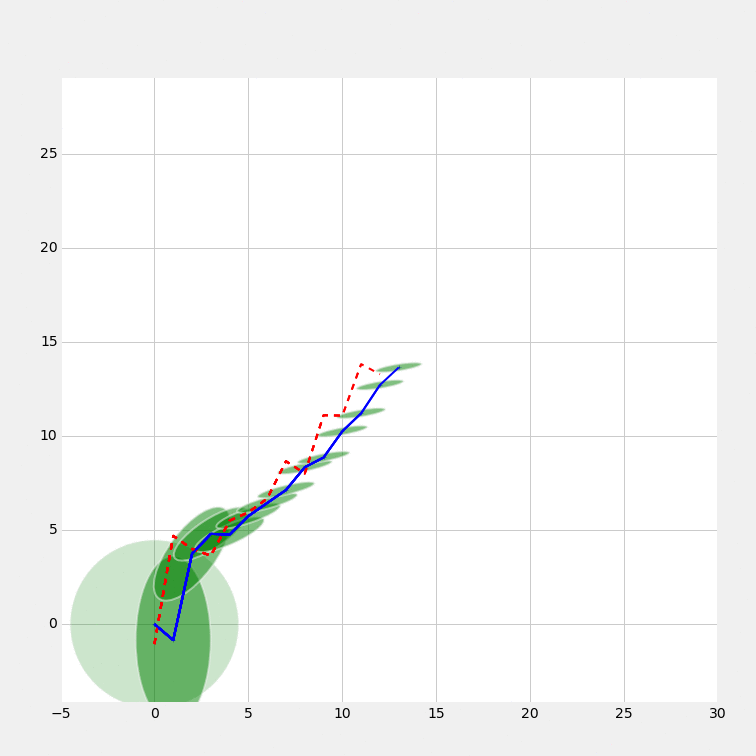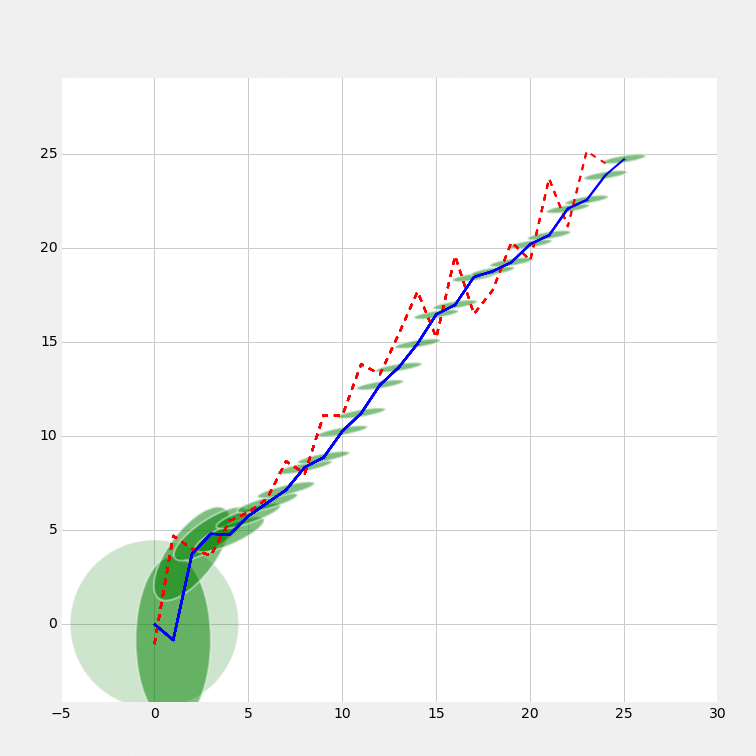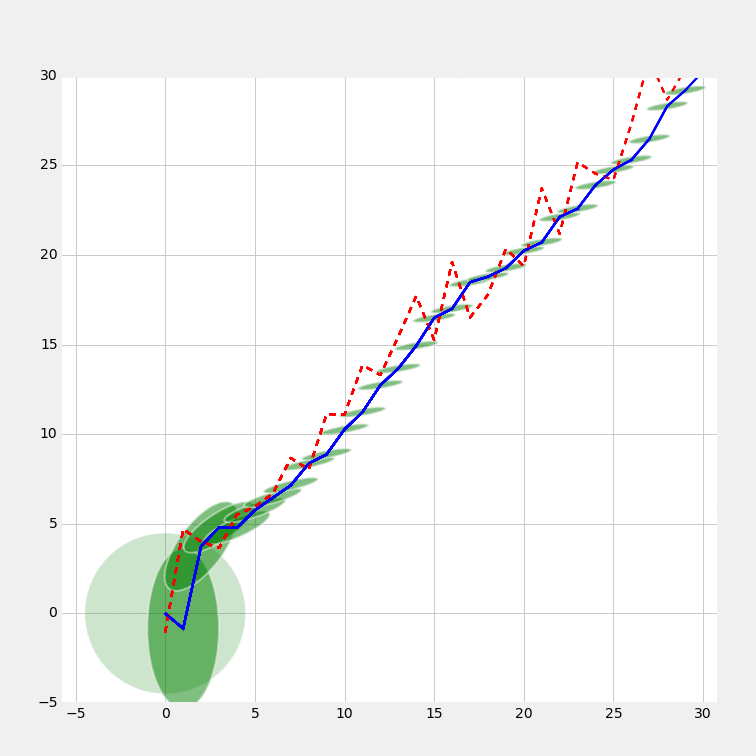
Related filters
- Extended Kalman filter - solves problem of the nonlinear model
- Unscented Kalman filter - better than EKF if the model is highly nonlinear
- Kalman–Bucy filter - continuous time version of the Kalman filter
- Hybrid Kalman filter - continuous-time models, discrete-time measurements
Summary
Disadvantages:
- Nonlinear models
- Initialization
- Discrete time
Advantages:
- Disadvantages can be solved by related filters. E.g.: Extended Kalman filter, Unscented Kalman filter ....
- The process noise or the measurement noise can be described in some specific problems
- Its recursive structure allows its real-time execution without storing observations or past estimates.
- Can be used in multidimensional space
Applications
- Attitude and Heading Reference Systems
- Autopilot
- Battery state of charge (SoC) estimation[40][41]
- Brain-computer interface
- Chaotic signals
- Tracking and Vertex Fitting of charged particles inParticle Detectors[42]
- Tracking of objects in computer vision
- Dynamic positioning
- Economics, in particular macroeconomics, time series analysis, and econometrics[43]
- Inertial guidance system
- Orbit Determination
- Power system state estimation
- Radar tracker
- Satellite navigation systems
- Seismology[44]
- Sensorless control of AC motor variable-frequency drives
- Simultaneous localization and mapping
- Speech enhancement
- Visual odometry
- Weather forecasting
- Navigation system
- 3D modeling
- Structural health monitoring
- Human sensorimotor processing[45]
- Attitude and Heading Reference Systems
- Autopilot
- Battery state of charge estimation
- Tracking of objects in computer vision
- Dynamic positioning
- Economics
- Inertial guidance system
- Orbit Determination
- Power system state estimation
- Radar tracker
- Satellite navigation systems
- Seismology
- Simultaneous localization and mapping
- Speech enhancement
- Visual odometry
- Weather forecasting
- Navigation system
- Structural health monitoring
- Human sensorimotor processing
Applications
References
- JURIĆ, Darko. Code of practice for project management for construction and development. Code Project [online]. [cit. 2015-03-28]. Dostupné z: http://www.codeproject.com/Articles/865935/Object-Tracking-Kalman-Filter-with-Ease
- Kalman Filters and Random Signals in Python. LABBE, Roger. [online]. [cit. 2015-03-28]. Dostupné z: http://nbviewer.ipython.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb
- Kalman filter. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, 2001- [cit. 2015-03-29]. Dostupné z: http://en.wikipedia.org/wiki/Kalman_filter
deck
By Tomáš Šabata
deck
- 1,188

