Dynamic modulation of actomyosin contractility and cortical flow by filament recycling
Will McFadden - Feb 8, 2017
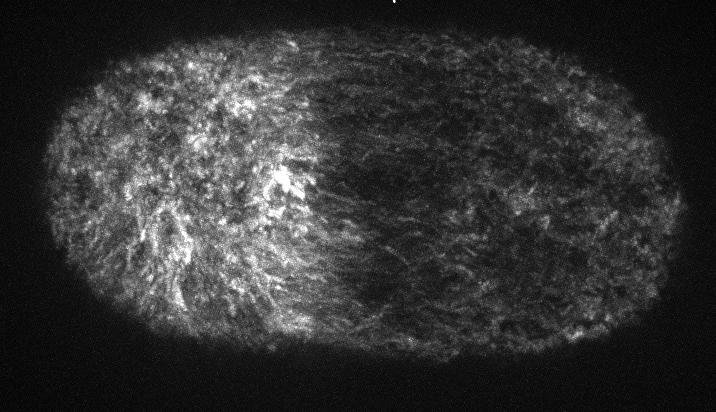
Cells reorganize their contents and change shape through a process called cortical flow
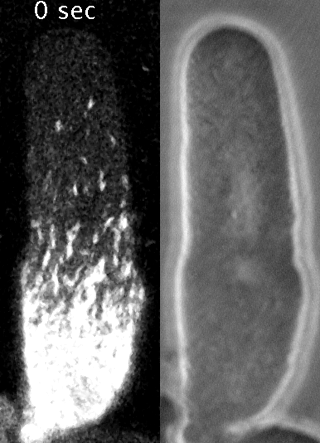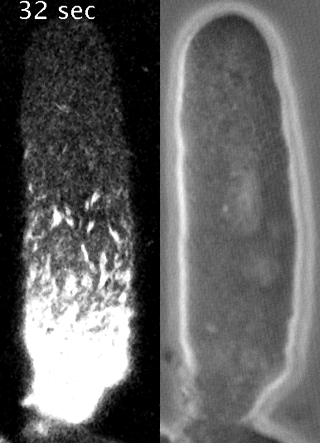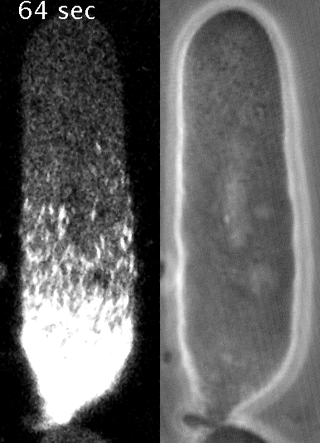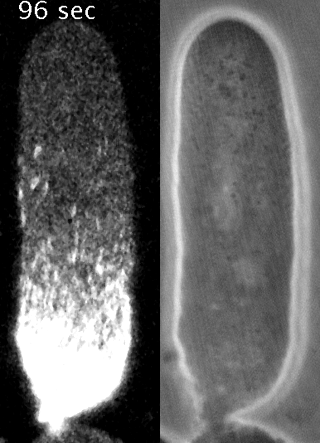
Yumura et al. 2013
Amoeboid migration
Cell polarization
Ed Munro
Berhndt et al. 2012
Epithelial spreading
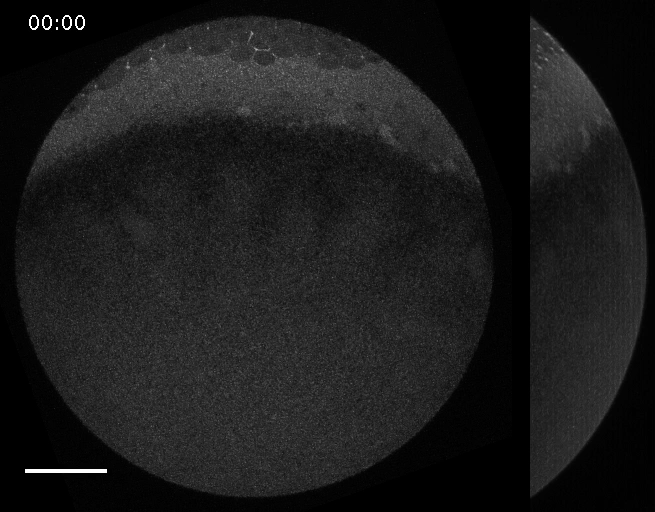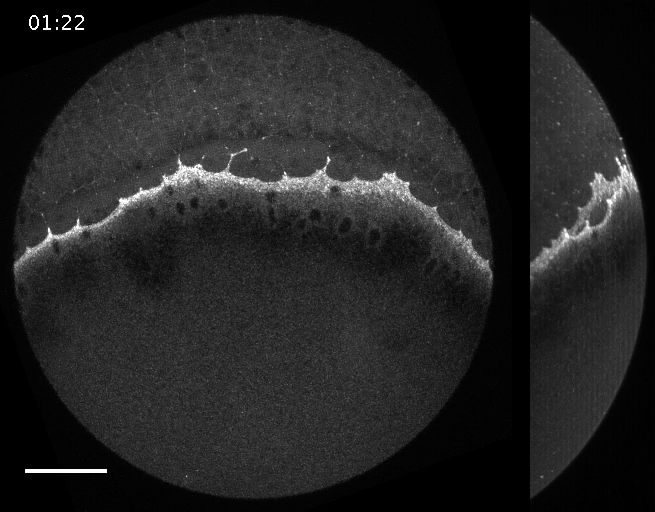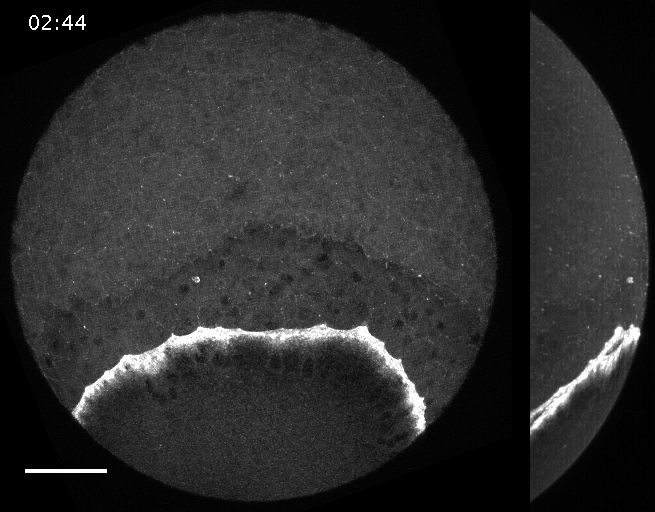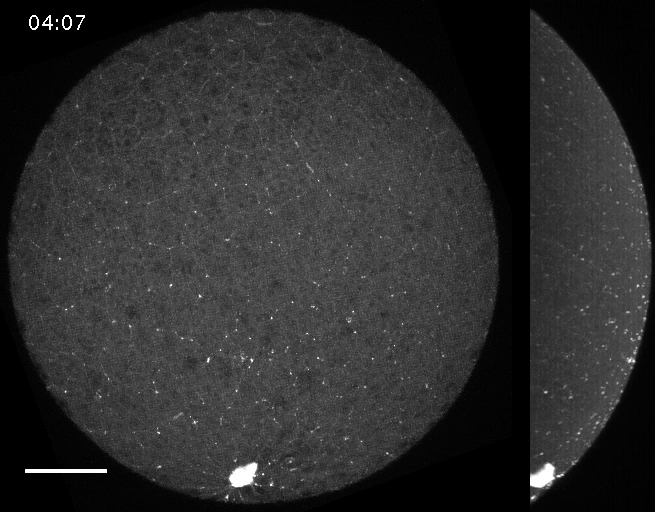
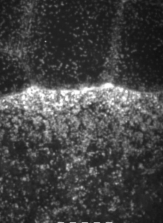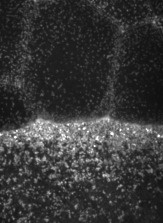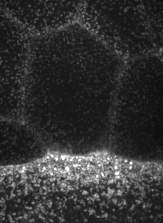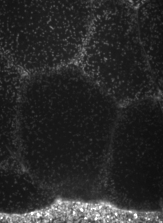
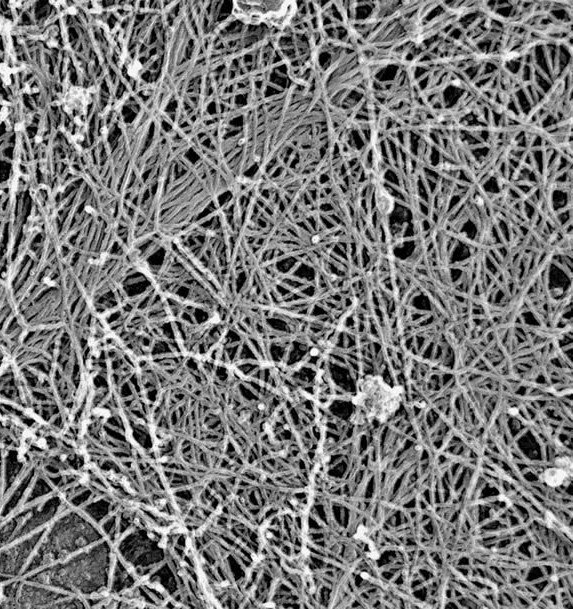
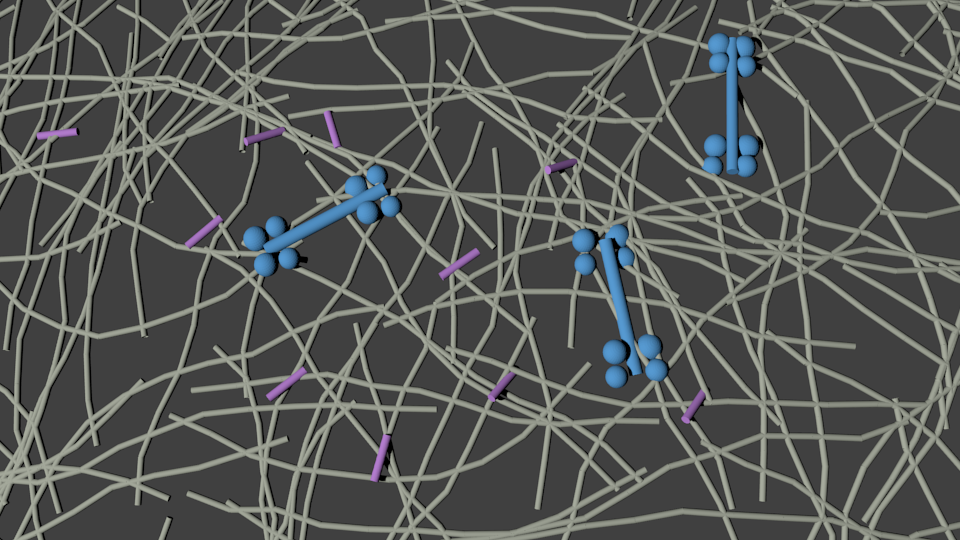
The machinery of cortical flow is the cortical actomyosin cytoskeleton
Christopher Beck
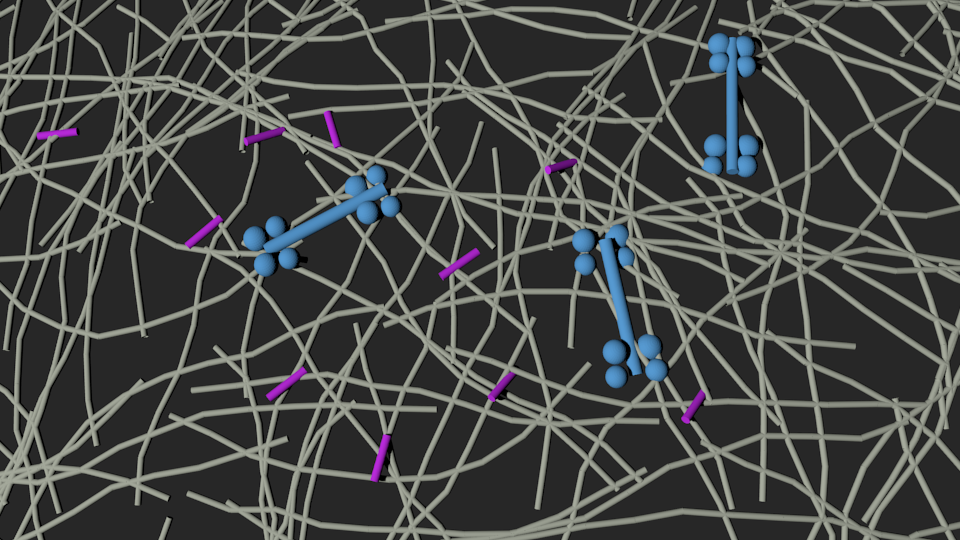
cross-linkers
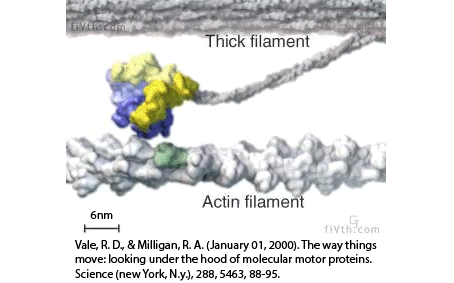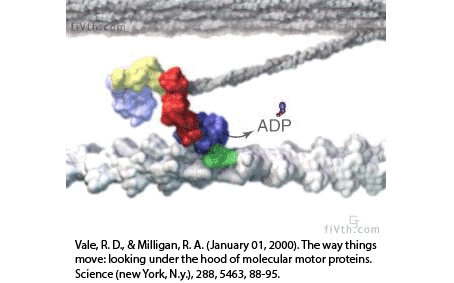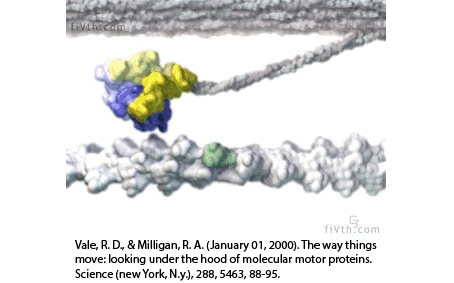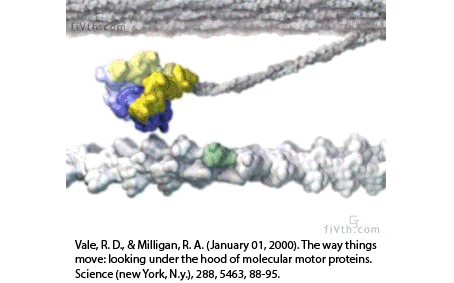
actin filaments
myosin motors
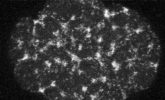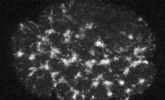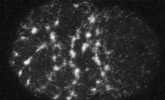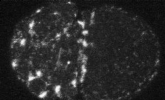
electron micrograph of cortical actin network
The cytoskeletal cortex supports the cell in a web just below the cell surface
Filament cross-linking proteins transiently bind individual actin filaments together
Actin filaments and myosin motors interact to exert forces on the cortex
actin filament
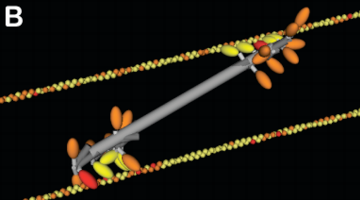
myosin motor
Jonathan Alberts
Filaments in the actomyosin cortex are highly dynamic and turnover rapidly
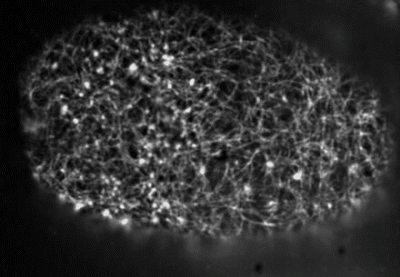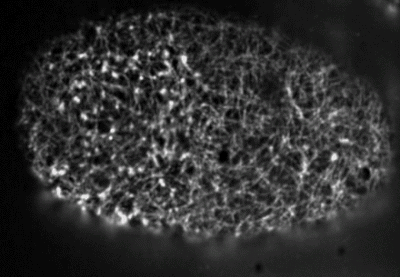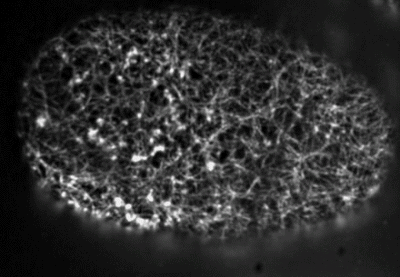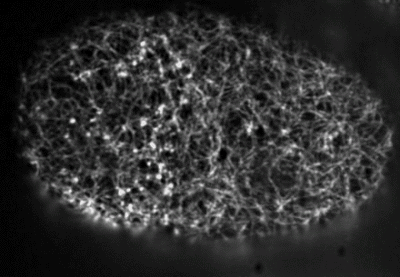
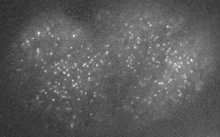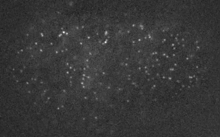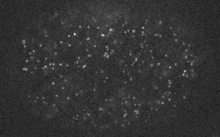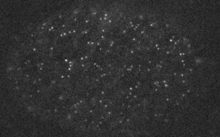
Actin networks remodel quickly
movie duration 30s
Actin monomers depolymerize rapidly
Robin, McFadden, Yao, Munro 2014
Active fluid theory describes flows of active material like the actomyosin cortex
Passive
Viscosity
Active Stress
myosin
Active fluids explain flow in terms of active stresses and passive viscosities
Passive
Viscosity
Active Stress
\dot{\gamma}=\frac{\sigma}{\eta}
flow rate
active stress
viscosity
The active stress and passive viscosity are assumed to arise from molecular properties of cytoskeletal networks
Passive
Viscosity
Active Stress
Cortical flow has been successfully described as an active fluid in which the active stress depends on presence of myosin motors.
Mayer et al. 2010
myosin motors
Passive
Viscosity
Active Stress
force imbalance
cortical flows
There's a gulf between the active fluid description and the molecular details
Active fluid theory
Molecular details
Passive
Viscosity
Active Stress
The theory doesn't explain how myosin generates stress or how actin passively deforms
My goal was to construct a minimal model of filaments and motors that could explain the emergence of active stress and passive vicosity.
- Actin filaments
- Cross-linking
- Myosin motors
- Actin turnover
Actin filaments are semi-flexible polymers with asymmetric compliance
Lenz Gardel Dinner New J Phys 2012
L
Worm-like chain model
soft linear compression
rigid linear extension
L
Mimicking cross-linker dynamics via a frictional interaction between filaments
Mimicking motor activity via an effective force at a subset of intersections
Samantha Stam
Lenz Gardel and Dinner New J Phys 2012
linear approximation
active motor
passive cross-linker
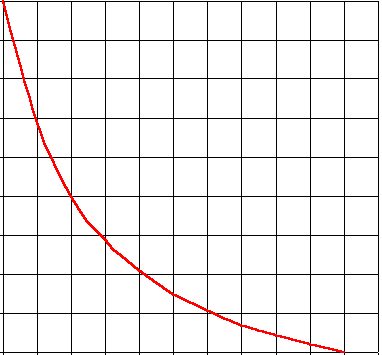
motor force
walking rate
These minimal assumptions are sufficient to generate macrocscopic contraction
compressed
extended
Goal: Use molecular scale model to derive macroscopic theory of flow
Passive
Viscosity
Active Stress
Passive
Viscosity
Active Stress
split up the problem
\dot{\gamma}=\frac{\sigma}{\eta}
flow rate
First, let's inspect the behavior of the network in the absence of turnover
- Actin filaments
- Cross-linking
- Myosin motors
- Actin turnover
In the absence of turnover, actin networks exhibit viscous flow on intermediate timescales, but ultimately tear
extensional force
~1/viscosity
Passive
Viscosity
relaxed
extended
In the absence of turnover, active networks build up force, but they lose connectivity and can't sustain it
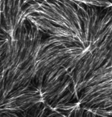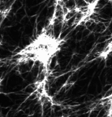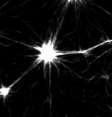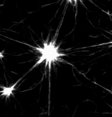
Murrell and Gardel 2012
in vitro actomyosin contraction
Active Stress
compressed
extended
In both the passive and active case, there is a mechanical reasoning behind the timescales over which force builds up and dissipates.
Active Stress
Passive
Viscosity
This model still hasn't accounted for the dynamic turnover of filaments
cells must turnover their actin to maintain flows
Preventing filament turnover stalls flows and leads to cortical tearing
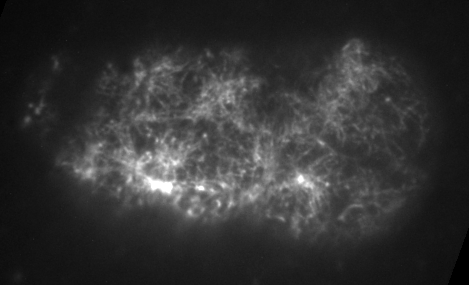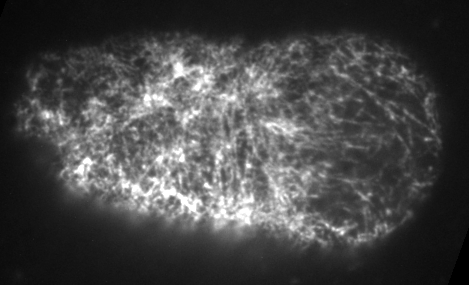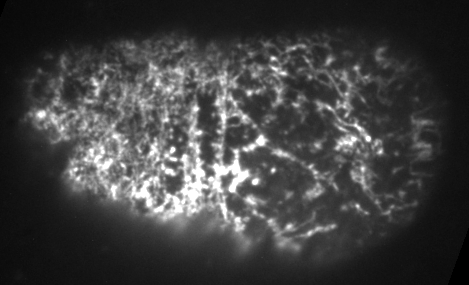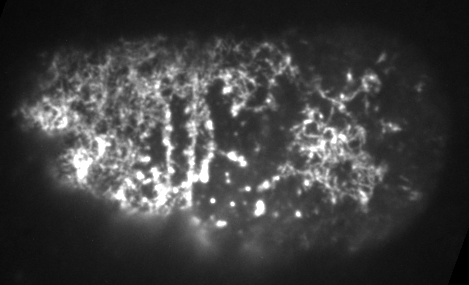
Dr. Jonathatn Michaux
japlakinolide treatmentsWhat happens when I introduce highly simplified filament turnover?
recycling time
or
turnover time
In passive networks: recycling prevents tearing, and tunes passive viscosity
Passive
Viscosity
Turnover time
Viscosity
Recycling allows active networks to produce sustained stress against a boundary
Sustained Stress
Turnover time
Active Stress
Turnover time tunes viscosity and stress
Next we can generate simulation that combine passive and active networks to see whether we can generate flows
Stress
Turnover time
Turnover time
Viscosity
Recycling allows persistent flows and tunes flow rate
slow turnover
fast turnover
active region
Flow
Time
Turnover time
Flow velocity
Passive
Viscosity
Active Stress
faster turnover
Can we explain the biphasic dependence of flow speed in terms of the dependencies of active stress and passive viscosity?
\dot{\gamma}=\frac{\sigma}{\eta}
flow rate
viscosity
active stress
Viscosity
Active Stress
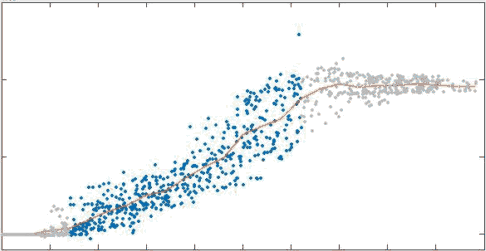
Ratio of active stress and viscosity as a function of turnover time should predict flow speed
\dot{\gamma}=\frac{\sigma}{\eta}
flow rate
viscosity
active stress
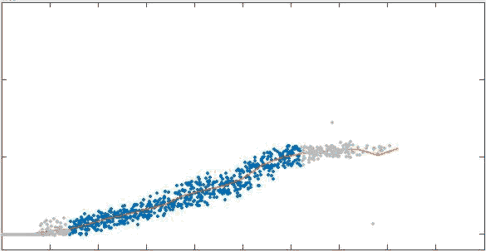
Because these are simulations, I can vary parameters and remeasure stress and viscosity
\tau_c
\tau_a
\sigma_m
\eta_c
Viscosity
Active Stress
This basic form of the active stress and viscosity dependence is a general property of these networks
a
We can use this model to understand the phase space of cortical flow
inert
tearing
Elastic to Viscous Transisiton Time
Turnover Time
Flow Speed
inert
turnover independent flows
flows
\tau_c/\tau_a
\tau_r/\tau_a
The simulations are predicting a pretty striking transition in flow speed between fast and slow turnover
Turnover time
Flow velocity
very slow turnover
This makes experimental predictions about what would happen as we vary turnover time in real cells
conclusions and future directions
this work offers a theoretical framework for understanding cortical flows
it sets up some experiments to test both quantitative and qualitative predictions
it might help explain what needs to be controlled to generate synthetic systems
Michele Wittels
Margaret Gardel, Ron Rock, Michael Glotzer, Aaron Dinner
Suggested experimental test
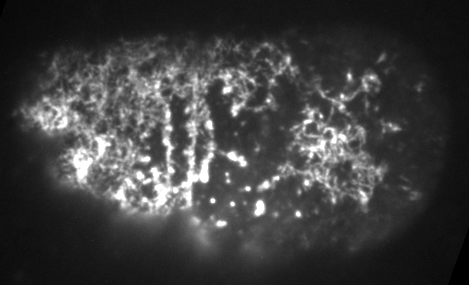
There's also a threshold timescale for turnover's impact on effective viscosity
\tau_c
There is an optimum turnover time that maximizes the steady state stress
\tau_a
\tau_a
Actin and myosin are the powerhouse behind force production in our muscles
myosin
aligned actin
aligned actin
Flows arise from active motor working to rearrange a passive filament network
Passive
Active
Mayer et al. 2010
Myosin
Myosin motors generates local stresses which drive flows
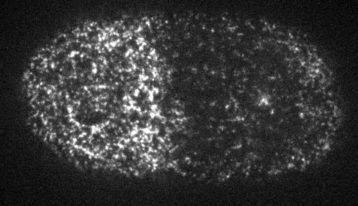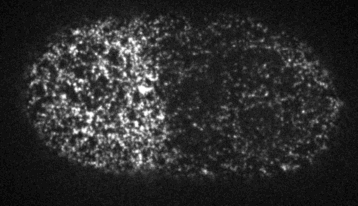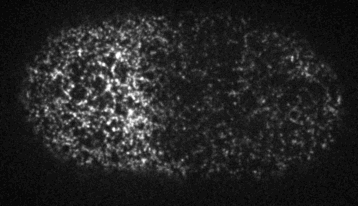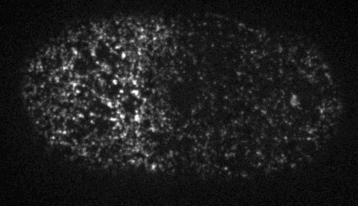
Passive
Active
strain thinning and tearing in passive networks being pulled on
position
filament velocity
Mechanical picture agrees with prior theoretical estimates for 2D networks
Head Levine Mackintosh, PRL 2003
I found an estimate for viscosity of networks with cross-link relaxation
\tau_c
1/\eta
In passive networks: recycling prevents tearing, and reduces steady state viscosity
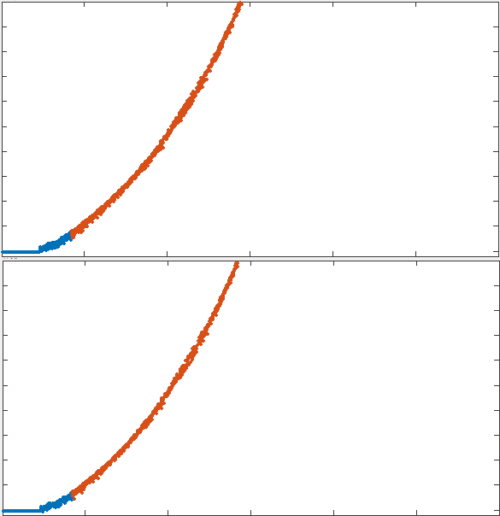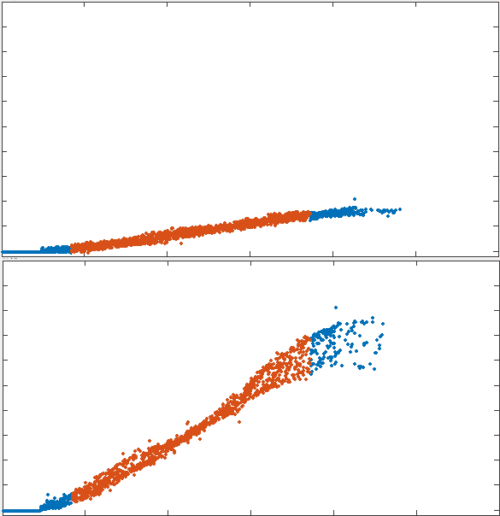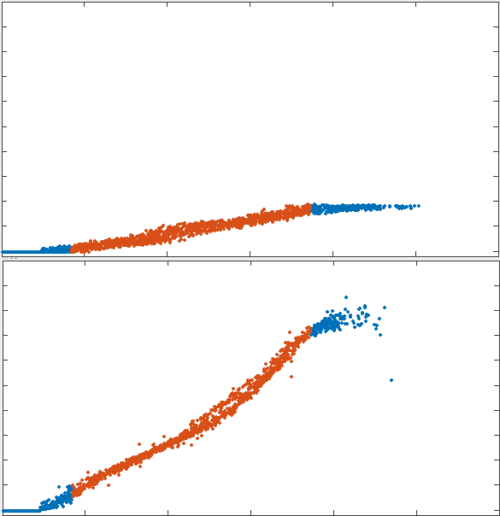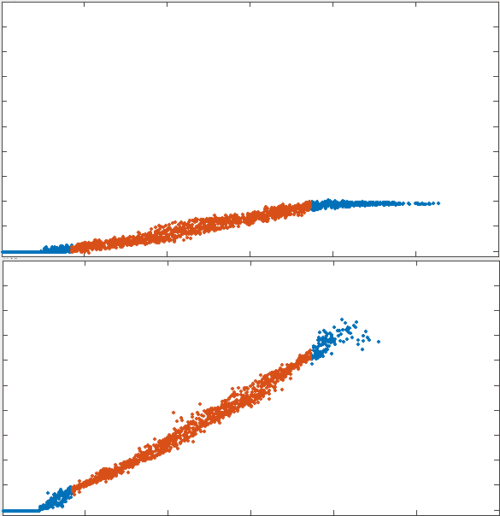
position
x velocity
x velocity
no recycling
tau = 10s
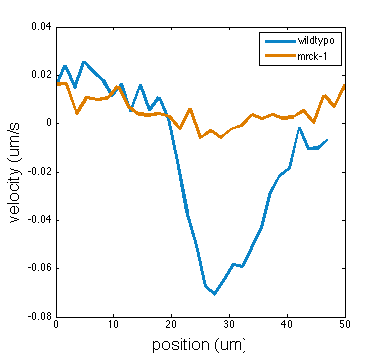
To test the theory we generated simulations of polarized networks
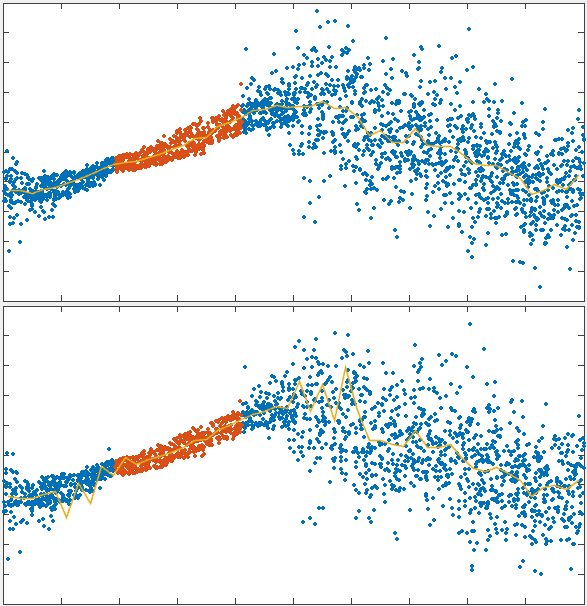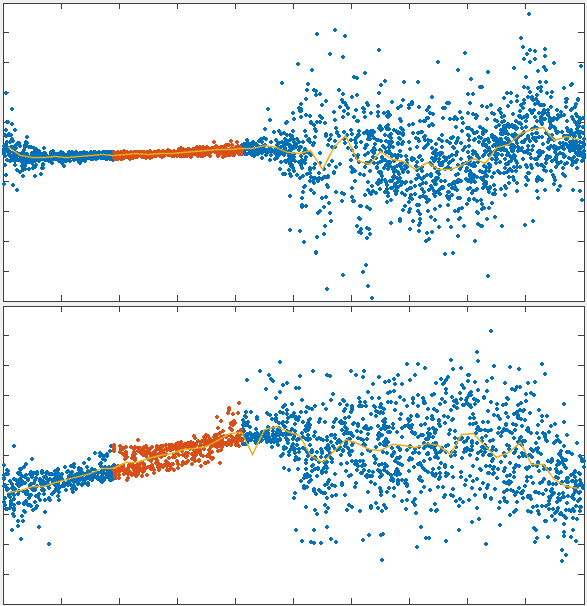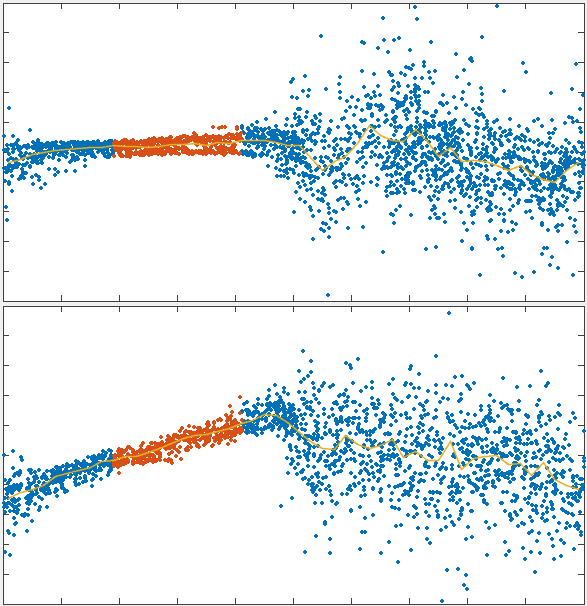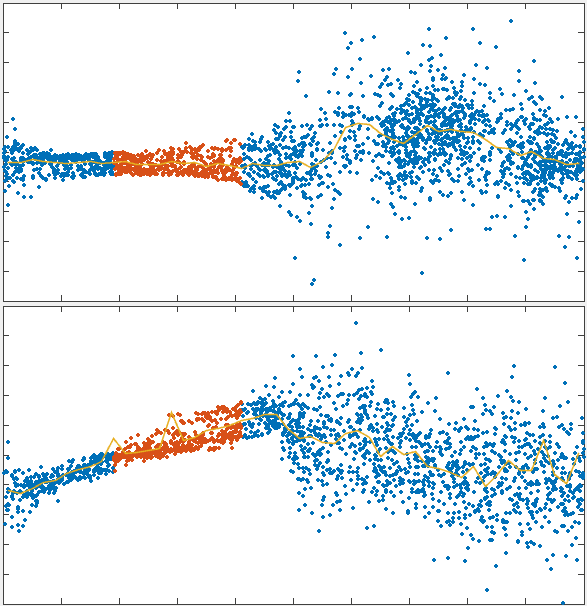
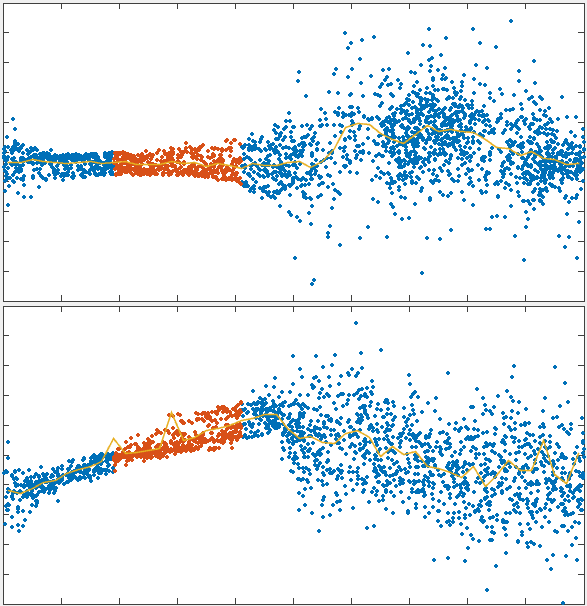
x velocity
x velocity
position
1000s
\tau_r
33s
active region
What is still missing from our description?
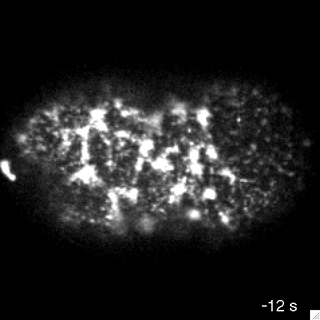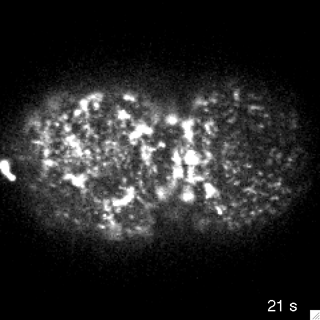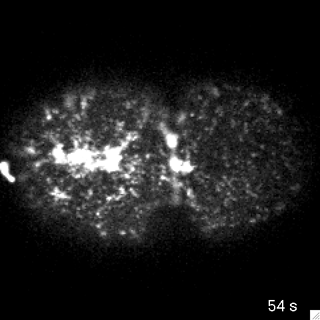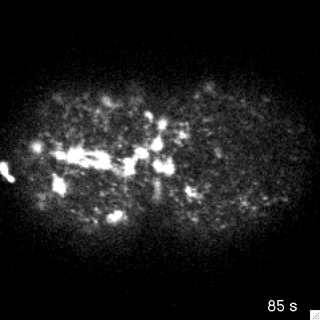
Actin filaments are highly dynamic and undergo regulated filament recycling: a key factor in sustaining cortical flows
cellular mechanisms of filament recycling
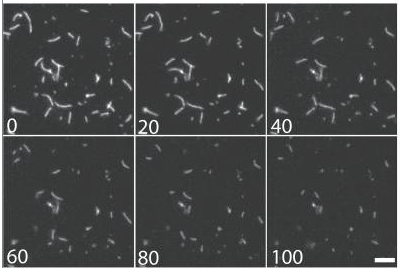
complete disassembly takes places in 100 s
Kuey et al. JCB 2008
We developed a method to measure filament recycling rates in vivo
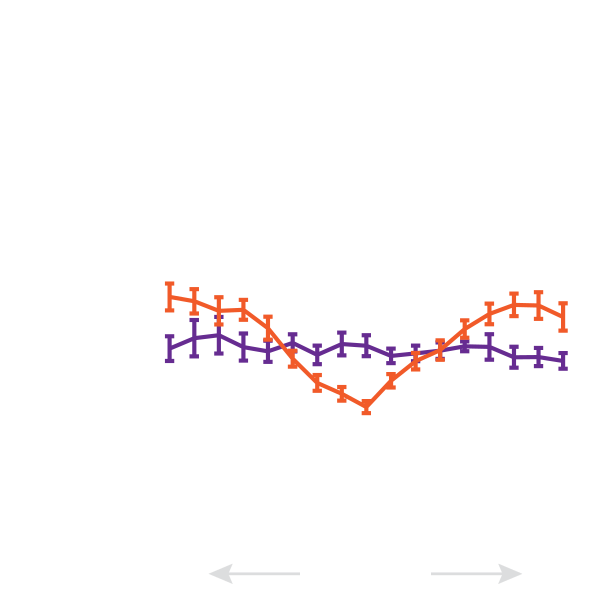
during division
pre-division
Robin et al. 2012
How to make your own shape
How can an organism rearrange itself?
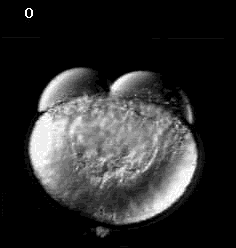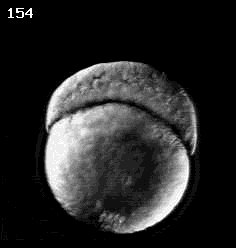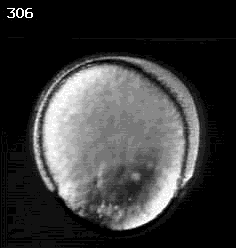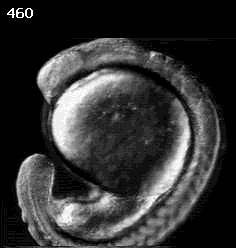
Don Kane (U. Rochester)
theseus
By wmcfadd2
