Streams à la carte

Extensible Pipelines with Object Algebras

Aggelos Biboudis¹, Nick Palladinos², George Fourtounis¹, Yannis Smaragdakis¹

University of Athens¹

Nessos Information Technologies²

(to appear at ECOOP'15)

Stream Libraries

functional-inspired pipelines
lazy

int sum = IntStream.of(v)
  .filter(x -> x % 2 == 0)
  .map(x -> x * x)
  .sum();

Stream Libraries

Great implementation variety, Java surprising!
- C# (LINQ), F#(Seq), Scala(Views) implement Pull-streams
- Java 8 implements Push-streams

int sum = IntStream.of(v)
  .filter(x -> x % 2 == 0)
  .map(x -> x * x)
  .sum();

What's Missing?

Fixed behavior and operators
- Push-vs-Pull implementation
- Java 8 doesn't accept custom operators

int sum = IntStream.of(v)
  .filter(x -> x % 2 == 0)
  .map(x -> x * x)
  .sum();

Why un-fix the behavior?

operators naturally push or pull ⇒ variable performance
to mix-in behaviors e.g.:
- log with push
- fuse with pull
- blocking or not with push or pull

avoiding other pathological cases

Iterator<Long> iterator = Stream
    .of(v)
    .flatMap(x -> Stream.iterate(0L, i -> i + 2)
                        .map(y -> x * y))
    .iterator();

iterator.hasNext(); // Out-of-memory :-(

Expression problem

http://homepages.inf.ed.ac.uk/wadler/papers/expression/expression.txt

Object Algebras: A design pattern to the rescue

https://www.cs.utexas.edu/~wcook/Drafts/2012/ecoop2012.pdf

An abstract factory

interface ExpFactory {
  Exp lit(int x);
  Exp add(Exp e1, Exp e2);
}

A generic factory

interface ExpFactory<Exp> {
  Exp lit(int x);
  Exp add(Exp e1, Exp e2);
}

An expression

<Exp> Exp mkAnExp(ExpFactory<Exp> f) {
    return f.add(f.lit(1), 
                 f.add(f.lit(2), f.lit(3)));
}

Algebraic Signatures

signature\ Exp

signature\ Exp

add : Exp \times Exp \rightarrow Exp

add : Exp \times Exp \rightarrow Exp

lit : Int \rightarrow Exp

lit : Int \rightarrow Exp

in the Object algebras realm

interfaces are named algebras
implementations are named factories
new cases (by extending the algebra)
new functions (by implementing the algebra)

we propose

A library
Inspired by Object Algebras
Provide extensible streams with:
- Pluggable operators
- Pluggable behaviors
- Mixedin behaviors
Affect performance (in a good way)

What is the object algebra of Streams?

interface StreamAlg<C<_>> {
    <T>     C<T> source(T[] array);
    <T, R>  C<R> map(Function<T, R> f, C<T> s);
    <T, R>  C<R> flatMap(Function<T, C<R>> f, C<T> s);
    <T>     C<T> filter(Predicate<T> f, C<T> s);
}

(for intermediate operators)

What is the object algebra of Streams?

interface ExecStreamAlg<E<_>, C<_>> 
extends StreamAlg<C> 
{
  <T> E<Long> count(C<T> s);
  <T> E<T>    reduce(T identity, 
                     BinaryOperator<T> acc, C<T> s);
}

(for terminal operators)

How do you extend streams?

Add new operators (by extending the algebra)

interface TakeStreamAlg<C<_>> extends StreamAlg<C> {
    <T> C<T> take(int n, C<T> s);
}

Add new behavior (by implementing the algebra)

class PushFactory implements StreamAlg<Push>

Let's use a stream

PushFactory alg = new PushFactory();

int sum = alg.sum(
           alg.map(x -> x * x,
            alg.filter(x -> x % 2 == 0,
             alg.source(v)))).value;

Streams a la carte

<E, C> E<Long> cart(ExecStreamAlg<E, C> alg) {
    return alg.reduce(0L, Long::sum,
            alg.flatMap(x -> 
             alg.map(y -> x * y, alg.source(v2)),
              alg.source(v1)));
}

Declaring streams: reducing a Cartesian product

cart(new ExecPushFactory()).value;
cart(new ExecPullFactory()).value;
cart(new ExecFusedPullFactory()).value;
cart(new LogFactory<>(new ExecPushFactory())).value;
cart(new LogFactory<>(new ExecPushFactory())).value;
cart(new ExecFutureFactory<>(new ExecPushFactory())).get();
cart(new ExecFutureFactory<>(new ExecPullFactory())).get();

Using streams with various factories

object algebras are for construction

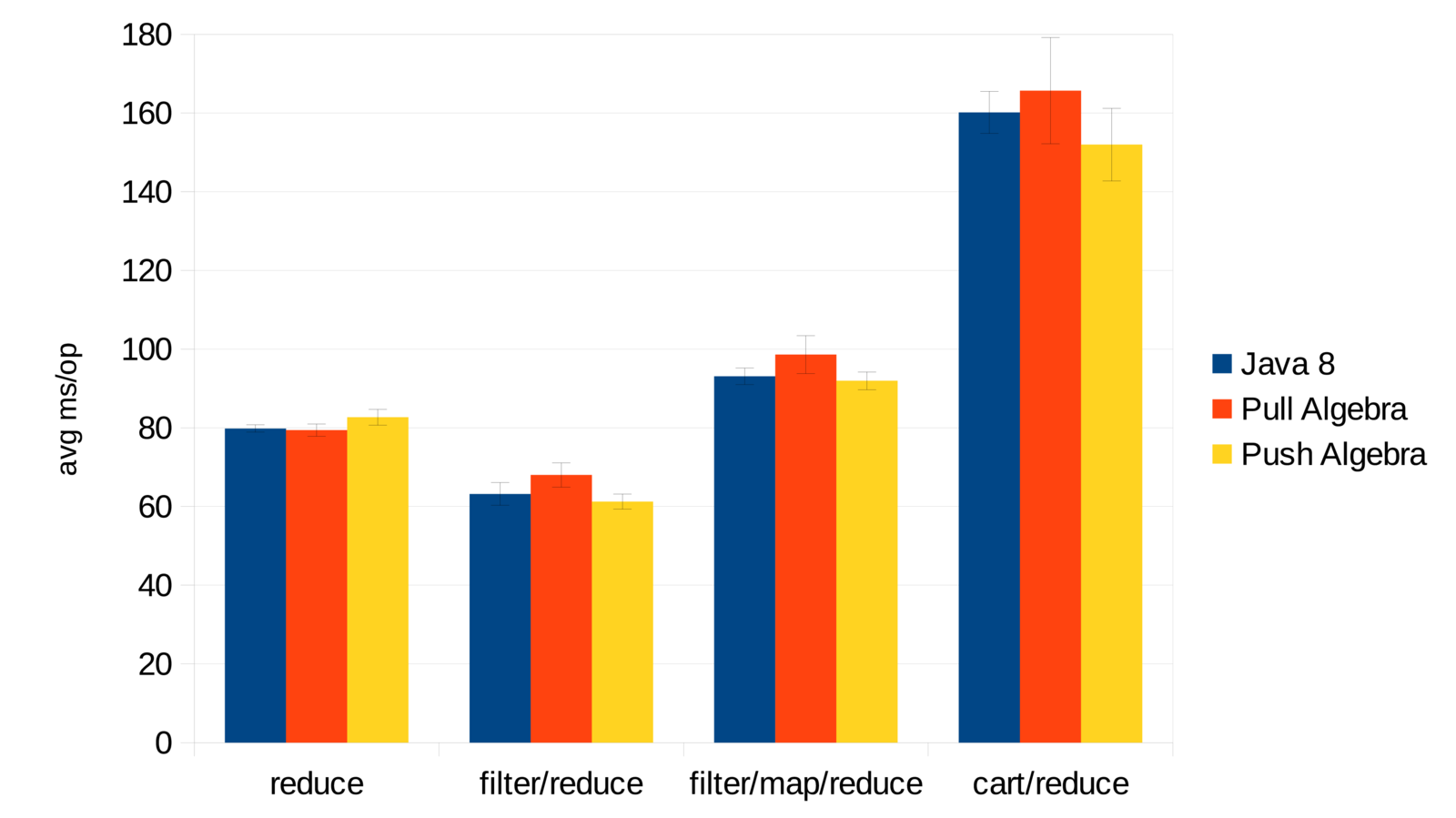
an algebra that fuses maps&filters

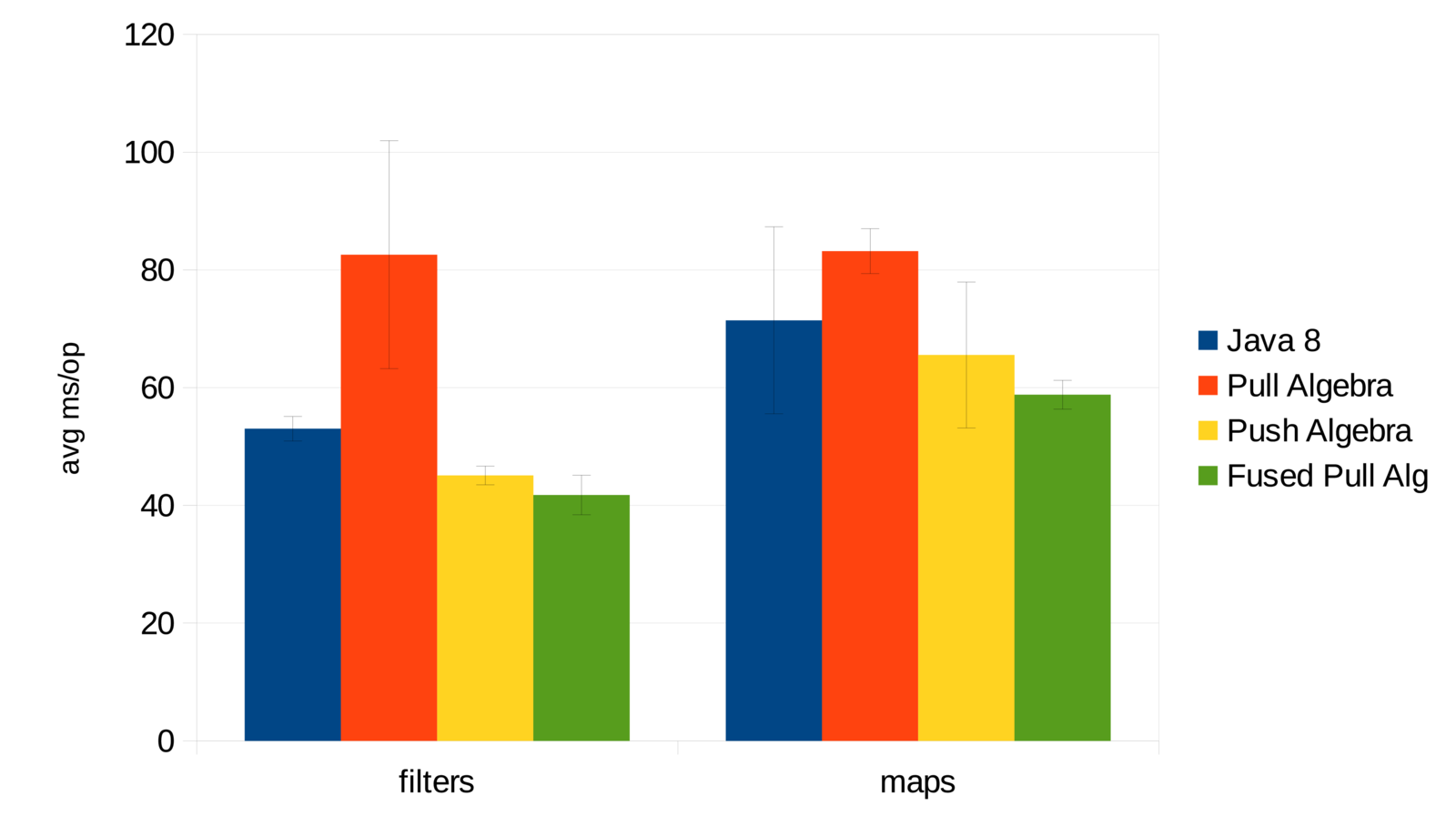
sometimes we need fully fledged pull

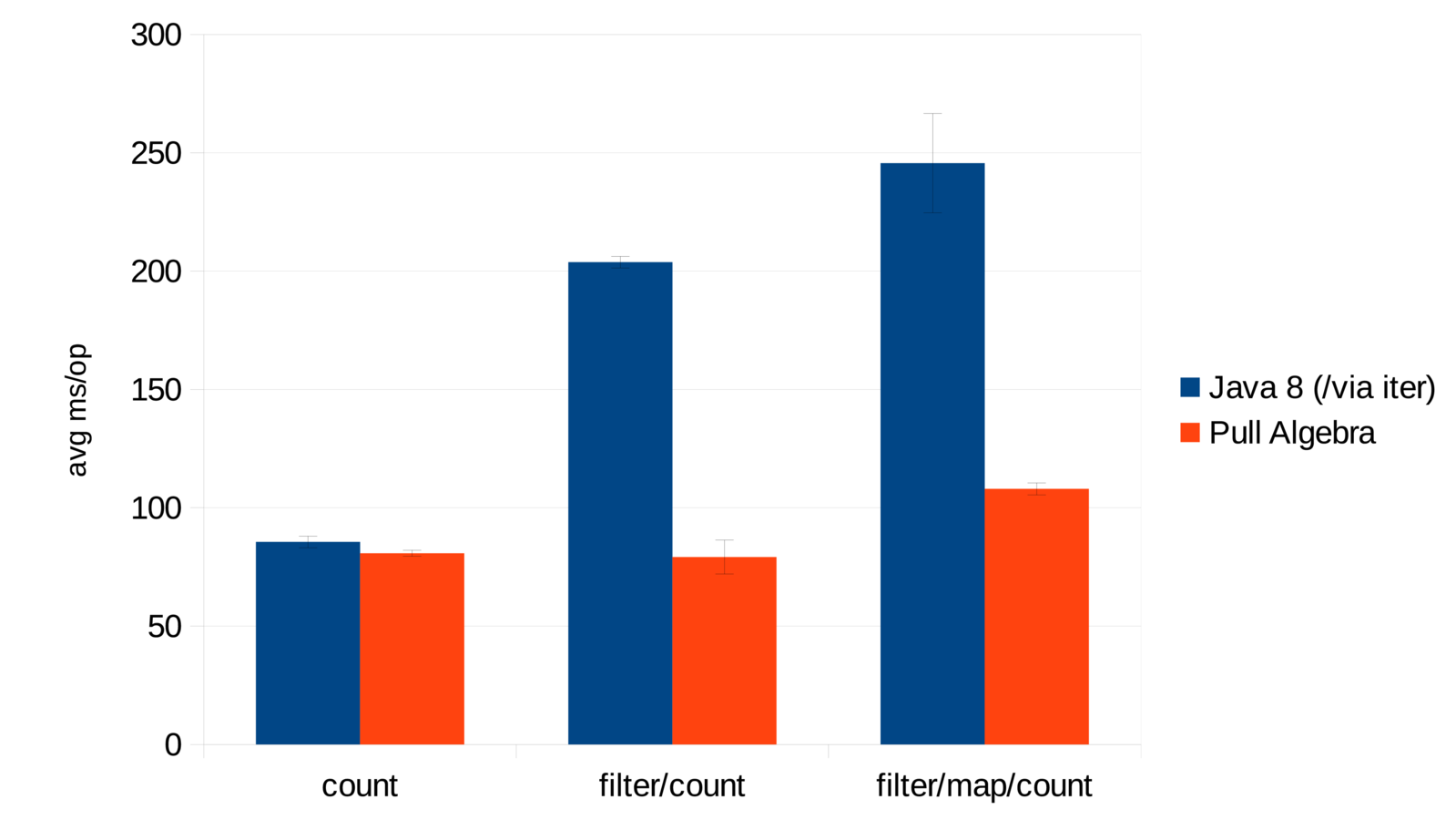
our pathogenic case from earlier with large nested stream

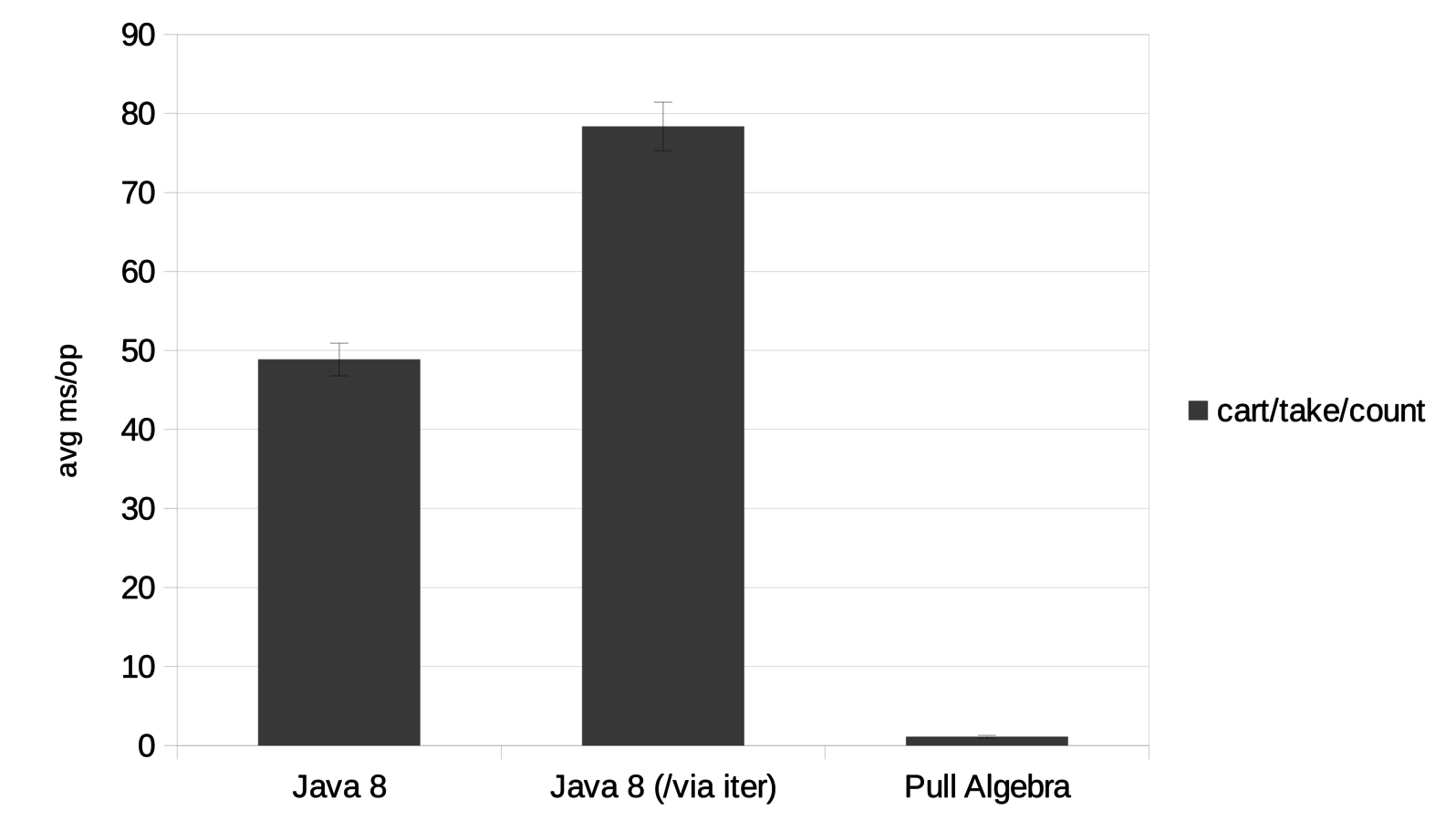
How did we encode higher-kinded types?

interface StreamAlg<C> {
  <T>    App<C,T> source(T[] array);
  <T, R> App<C,R> map(Function<T,R> f, App<C,T> app);
  <T, R> App<C,R> flatMap(Function<T, App<C,R>> f, 
                          App<C,T> app);
  <T>    App<C,T> filter(Predicate<T> f, App<C,T> app);
}

interface App<C, T> {}

interface StreamAlg<C<_>> {
    <T>     C<T> source(T[] array);
    <T, R>  C<R> map(Function<T, R> f, C<T> s);
    <T, R>  C<R> flatMap(Function<T, C<R>> f, C<T> s);
    <T>     C<T> filter(Predicate<T> f, C<T> s);
}