Topiary and the Art of Origami
Exploring decision trees with recursion schemes
@_zainabali_
Zainab Ali
Predicting survival on the Titanic
- Shipwreck
- Over 60% died
- Not enough lifeboats
- Stochastic
- Can we predict survival?
The Journey
- basic predictions
- use decision trees
- matryoshka
- anamorphisms
- catamorphisms
- hylomorphisms
- cost complexity pruning
Input Example
Output Label
case class Example(
gender: Gender,
age: Age,
ticketClass: TicketClass,
familySize: FamilySize
)
sealed trait Label
case object Survived
extends Label
case object Died
extends Label
1000 examples
binary classification
Hypothesis
def predict(example: Example): Label
- train on a subset of examples
- test on the rest
Hypothesis: Everyone Dies
def predict(example: Example): Label = Died
Risk
def risk(predictions: Map[Int, Label],
actual: Map[Int, Label]): Double = {
predictions.map {
case (id, prediction) =>
if (prediction != actual(id)) 1.0 else 0.0
} / predictions.size
}
Fraction of incorrect predictions
Risk: Everyone Dies
39.5%
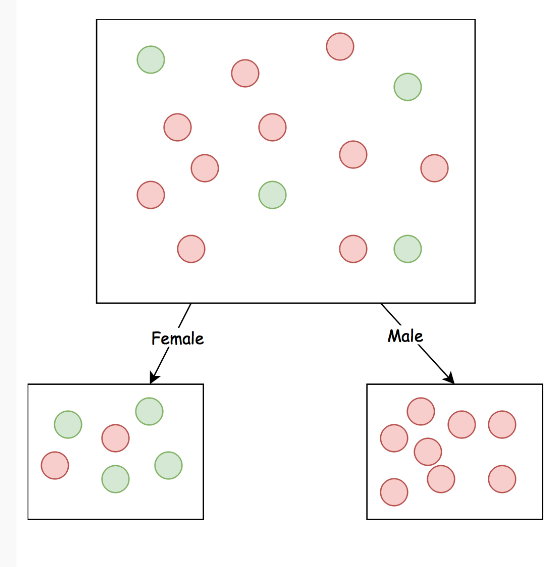
Females Survive
def predict(example: Example): Label =
example.gender match {
case Female => Survived
case Male => Died
}
Risk: Females Survive
24% (-15.5)
Entropy
Matryoshka
Recursion schemes

Decision tree
sealed trait Tree
case class Leaf(label: Label) extends Tree
case class Node(feature: Feature,
children: Map[Value, Tree]) extends Tree
sealed trait TreeF[A]
case class Leaf[A](label: Label) extends TreeF[A]
case class Node[A](feature: Feature,
children: Map[Value, A]) extends TreeF[A]
Fix
case class Fix[F[_]](unFix: F[Fix[F]])
val tree: Fix[TreeF] = Fix(Node(gender, Map(
"male" -> Fix(Leaf[Fix[TreeF]](Died)),
"female" -> Fix(Leaf[Fix[TreeF]](Survived))
)))
type Tree = Fix[TreeF]

It needs a Functor
implicit val treeFunctor: Functor[TreeF] =
new Functor[TreeF] {
def map[A, B](fa: TreeF[A])(f: A => B): TreeF[B] =
fa match {
case Leaf(l) => Leaf(l)
case Node(feature, children) =>
Node(feature, children.mapValues(f))
}
}
Anamorphism
type Coalgebra[F[_], A] = A => F[A]
def ana[F[_]: Functor, A](a: A)(
coalgebra: Coalgebra[F, A]): Fix[F]
Generalized unfold

Building the tree
type Input = (List[Example], Set[Feature])
val build: Coalgebra[TreeF, Input] = {
case (examples, features) =>
if(features.nonEmpty) {
val (feature, maxGain) = maxGain(examples, features)
val nextFeatures = features - feature
val nextExamples = groupByValue(examples, feature)
Node(feature, nextExamples.mapValues(xs =>
(xs, nextFeatures)))
} else {
Leaf(mostCommonLabel(examples))
}
}
val tree: Tree = (examples, features).ana(build)
Anamorphism
val tree: Tree = (examples, features).ana(build)
Prediction: exploring a path
def explore(example: Example):
Coalgebra[Label Either ?, Tree] =
_.unFix match {
case Leaf(label) => Left(label)
case Node(feature, children) =>
Right(children(value(feature, example)))
}Anamorphism with Either
Prediction: exploring a path
val lizWalton: Example = Example(Adult, Female, ...)
val path: Fix[Label Either ?] = tree.ana(explore(lizWalton))
//path = Fix(Right(Fix(Right(...(Fix(Left(Label.Survived))))
Catamorphism
type Algebra[F[_], A] = F[A] => A
def cata[F[_]: Functor, A](fix: Fix[F])(
algebra: Algebra[F, A]): A
Generalized fold

Prediction: collapsing the path
val collapse: Algebra[Label Either ?, Label] = _.merge
val prediction = path.cata(collapse)
//prediction = SurvivedHylomorphism
def hylo[F[_]: Functor, A, B](a: A)(
algebra: Algebra[F[_], B],
coalgebra: Coalgebra[F[_], A]): B
Generalized refold

Hylomorphism
def predict(tree: Tree)(example: Example): Label =
tree.hylo(collapse, explore(example))
Risk: Decision Tree (training)
15.1%
Risk: Decision Tree
(test)
24.0% (-0.0)
Overfitting
topiary time!
Cost Complexity Pruning
- Annotate T0 with label counts
- Annotate with cost
- Find minimum cost
- Snip off node with minimum cost to create T1
- Repeat 3 and 4 to get T2 ...
- Create a series of subtrees T0, T1, T2 ... Leaf
Cost
- current risk
- resubstitution risk of replacing node with leaf
- number of leaves removed
Tagging
case class AttrF[A, B](a: A, tree: TreeF[B])
implicit def attrFunctor[A]: Functor[AttrF[A, ?]] = ...
Tag with counts
type Counts = Map[Label, Int]
def buildCounts: Coalgebra[AttrF[Counts, ?], Input] = {
case (examples, features) =>
val counts = labelCounts(examples)
val tree = build((examples, features))
AttrF(counts, tree)
}
val tree = (examples, features).ana(buildCounts)
Tag with cost
case class CostInfo(
leafCount: Int,
risk: Int,
counts: Counts
)
val costInfo: Algebra[AttrF[Counts, ?], Attr[CostInfo]] = {
case AttrF(counts, t: Leaf(_)) =>
Fix(AttrF(leafCostInfo(counts, t), t))
case AttrF(_, t @ Node(_, children)) =>
Fix(AttrF(nodeCostInfo(children), t))
}
tree.cata(costInfo)
Another hylo!
val tree = (examples, features)
.ana(buildCounts)
.cata(costInfo)
val tree = (examples, features).hylo(buildCounts, costInfo)
Find min cost
val minCost: Algebra[AttrF[CostInfo, ?], Double] = {
case AttrF(_, Leaf(_)) => Double.PositiveInfinity
case AttrF(info, Node(_, children)) =>
(info.cost :: children.values).min
}
tree.cata(minCost)
Prune
def prune(minCost: Double):
Algebra[AttrF[CostInfo, ?], Attr[CostInfo]] = {
case AttrF(c, Leaf(l)) =>
Fix(AttrF(c, Leaf(l)))
case AttrF(info, n @ Node(_, children)) =>
if(info.cost == minCost) {
val leaf = makeLeaf(info)
Fix(AttrF(leafCostInfo(info.counts, leaf), leaf))
} else {
Fix(AttrF(nodeCostInfo(children), n))
}
}
tree.cata(prune(minCost))
Cost Complexity Pruning
val tree = (examples, features)
.hylo(buildCounts, costInfo)
val cost1 = tree.cata(minCost)
val subTree1 = tree.cata(prune(cost1))
val cost2 = subTree1.cata(minCost)
val subTree2 = subTree1.cata(prune(cost2))
...
Which subtree?
- Split data into training and validation
- Build trees on training data
- Validate on validation data
- Pick the subtree with the lowest risk
Risk: Pruned Tree
22.4% (-1.6)
Yay!
We've come a long way
- Anamorphisms
- Catamorphisms
- Hylomorphisms
Where to next?
- Dimensionality reduction
- Cross validation
- Ensemble methods
You may be interested in
- The code https://github.com/zainab-ali/titanic
- Matryoshka https://github.com/slamdata/matryoshka

We're hiring!
Thanks!
Topiary and the Art of Origami
By Zainab Ali
Topiary and the Art of Origami
Recursive data structures are a core tool of any functional programmer's toolkit, but they are also one of the most challenging. Budding functional programmers are plagued with nightmares of infinite recursion, mental stack overflows, and the terrifying fixed point. Recursion schemes, generalised folds and unfolds with exotic names and signatures, are a further hurdle to overcome. But past this hurdle there are many rewards. This talk uses the power of recursion schemes to predict survival on the Titanic. We will show that recursion schemes can be used to grow a decision tree and make predictions from it. Furthermore, they give us far more benefits than the basic folds or unfolds we would otherwise use. You will make use of many folds, unfolds and even refolds. Be prepared to exercise your skills in origami!
- 4,579



