Online Kernel Matrix Factorization
Motivation
- Fast growing of aviable information
- Databases with millions of instances
- Matrix Factorization (MF) as powerful analysis
Motivation (cont.)
- Most MF are suitable to extract linear patterns
- Kernel matrix factorization (KMF) methods are suitable to extract non-linear patterns
- KMF methods have high computational cost.
Matrix Factorization
Matrix factorization is a family of linear-algebra methods that take a matrix and compute two or more matrices, when multiplied are equal to the input matrix
X
=
W
H
Kernel Method
\Phi:\mathcal{X}\longmapsto\mathcal{F}
\Phi:x\longmapsto\Phi(x)
Kernels are fuctions that map points from a input space X to a feature space F where the non-linear patterns become linear
Kernel Method (cont.)
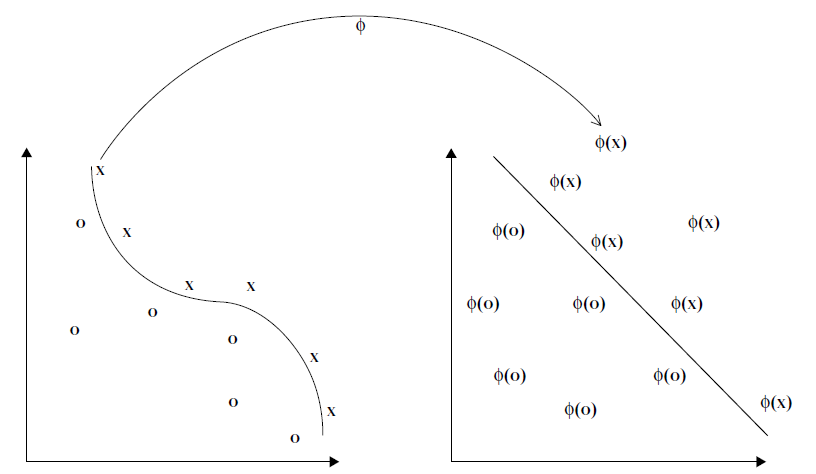
Kernel Trick
- Many methods can use inner-products instead of actual points.
- We can find a fuction that calculates the inner-product for a pair of points in fea
k(x,y)=\langle\Phi(x),\Phi(y)\rangle
Kernel Matrix Factorization
Kernel Matrix factorization is a similar method, however, instead of factorizing the input-space matrix, it factorizes a feature-space matrix.
\Phi(X)^T\Phi(X)
=
W_\phi
H
Problem
- The time and space required by Kernel Methods is quadratic in terms of the number of samples.
- This cost leads to the impossibility to apply this kind of methods to a large set.
- The challenge is to devise effective and efficient mechanisms to perform KMF.
Graphic Problem
\Phi(X)^T\Phi(X)
=
W_\phi
H
Graphic Problem
n\times n
\Phi(X)^T\Phi(X)
Main Objective
To design, implement and evaluate a new KMF method that is able to compute an kernel-induced feature space factorization to a large-scale volume of data
Specific Objectives
- To adapt a matrix factorization algorithm to work in a feature space implicitly defined by a kernel function.
- To design and implement an algorithm which calculates a kernel matrix factorization using a budget restriction.
Specific Objectives (cont.)
- To extend the in-a-budget kernel matrix factorization algorithm to do online learning.
- To evaluate the proposed algorithms in a particular task that involves kernel matrix factorization.
Contributions
- Design of a new KMF algorithm, called online kernel matrix factorization (OKMF).
- Efficient implementation of OKMF using CPU.
- Efficient implementation of OKMF using GPU.
- Online Kernel Matrix Factorization. Conference article presented in XX CIARP 2015.
- Accelerating kernel matrix factorization through Theano GPGPU symbolic computing. Conference article accepted in CARLA 2015.
Factorization
\Phi(X)=\Phi(B)WH
\Phi(X)\in \mathbb{R}^{l\times n}
\Phi(B)\in \mathbb{R}^{l\times p}
W\in \mathbb{R}^{p\times r}
H\in \mathbb{R}^{r\times n}
p\ll n
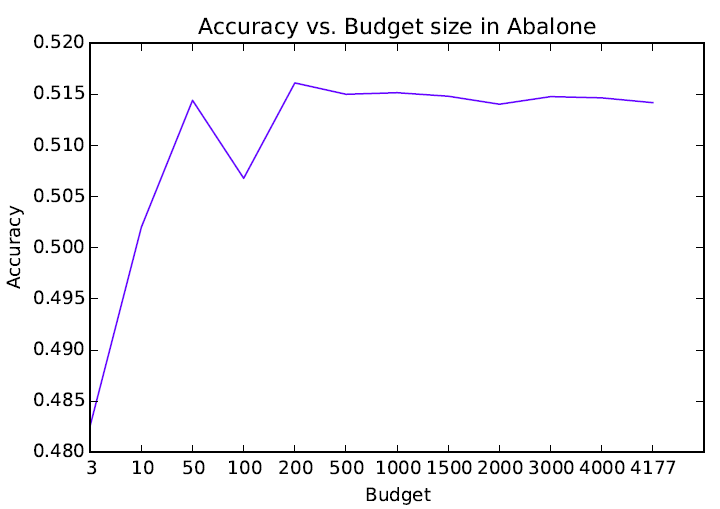
About the Budget
- The budget matrix is a set of representative points ordered as columns.
- The budget selection is made through random picking o p X matrix or by computing k-means with k=p.
Optimization Problem
\displaystyle
\min_{W,H}\frac{1}{2}\|\Phi(X)-\Phi(B)WH\|^2_F+\frac{\lambda}{2}\|W\|^2_F+\frac{\alpha}{2}\|H\|^2_F
SGD Optimization Problem
\displaystyle
\min_{W,h_i}\frac{1}{2}\|\Phi(x_i)-\Phi(B)Wh_i\|^2+\frac{\lambda}{2}\|W\|^2_F+\frac{\alpha}{2}\|h_i\|^2
SGD Update Rules
\displaystyle
h_t = (W^T_{t-1}k(B,B)W_{t-1}-\alpha I)^{-1}W^T_{t-1}k(Bx_t)
\displaystyle
W_t = W_{t-1} - \gamma(k(B,x_t)h^T_t-k(B,B)W_{t-1}h_th_t^T+\lambda W_{t-1})
OKMF Algorithm
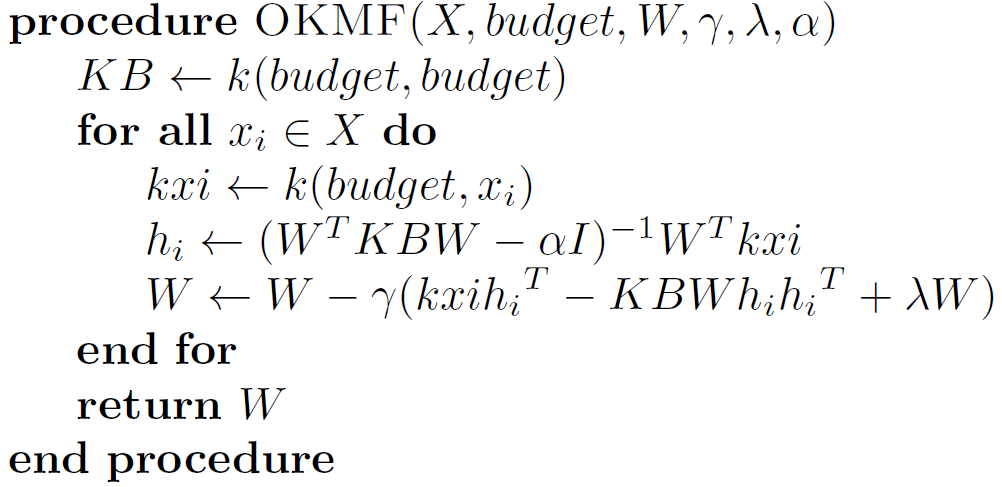
Experimental Evaluation
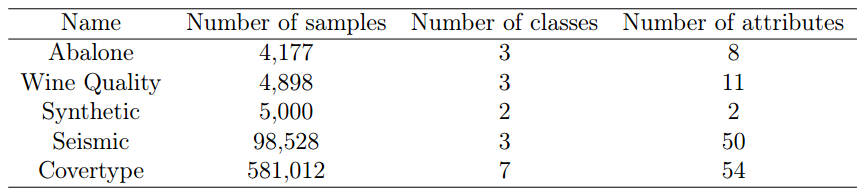
- A clustering task was selected to evaluate OKMF
- 5 data sets were selected, raging from 4177 to 58012 instances.
Performance Measure
The selected performance measure is the clustering accuracy, this measures the ratio between the number of correctly clustered instances and the total number of instances.
Compared Algorithms
- Kernel k-means
- Kernel convex non-negative factorization
- Online k-means (no kernel)
- Online kernel matrix factorization
Used Kernel Functions
Linear kernel
k(x,y)=x^Ty
Gaussian kernel
k(x,y)=\exp(-\frac{\|x-y\|^2}{2\sigma^2})
Parameter Tuning
- The learning rate, regularization and Gaussian parameters were tuned for OKMF in order to minimize the average loss of 10 runs.
- The Gaussian kernel parameter was tuned fro CNMF and Kernel k-means to maximize the average accuracy of 10 runs.
- The budget size of OKMF was fix to 500 instances
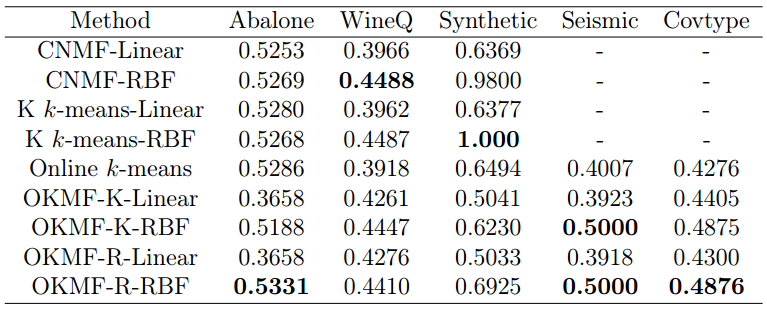
Results
- The experiments consists of 30 runs, the average clustering accuracy and average clustering time are reported.
Average Clustering Accuracy of 30 runs
Average Clustering Time of 30 runs (seconds)
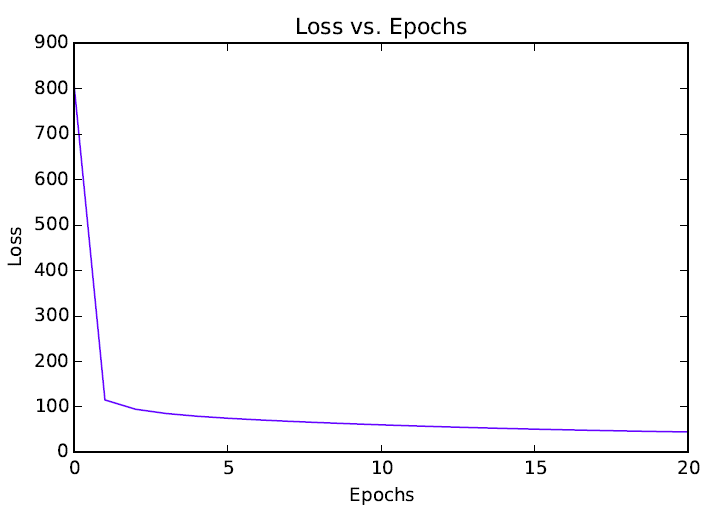
Loss vs. Epochs
Accuracy vs. Budget Size
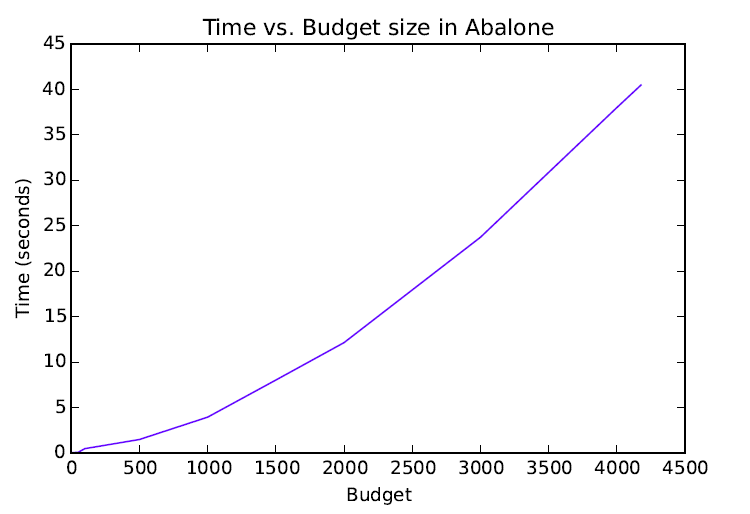
Time vs. Budget Size
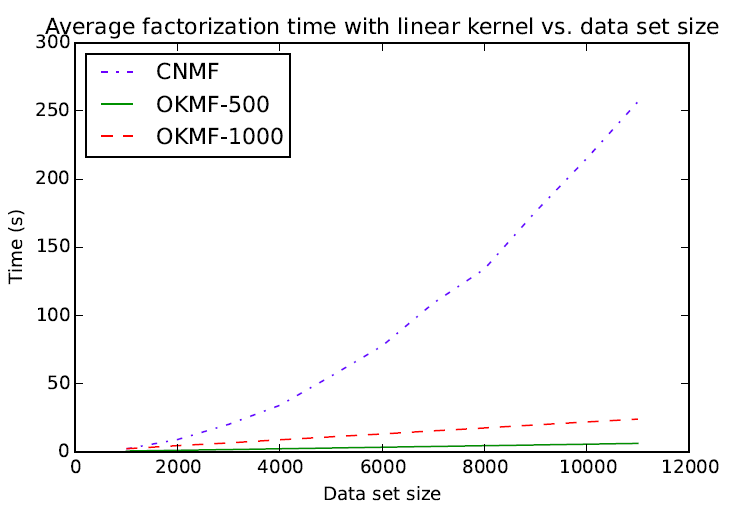
Avg. factorization time vs. dataset size (linear)
Conclusions
- OKMF is a memory efficient algorithm, it requires to store a matrix, which is better than a matrix if
- Also, SGD implies a memory saving, given OKMF stores a vector of size instead of a matrix of size
n\times n
p\times p
p\ll n
p
p\times n
Conclusions (cont.)
- OKMF has a competitive performance compared with other KMF and clustering algorithms in the clustering task.
- Exprimental results show OKMF can scale linearly with respect the number of instances.
- Finally, the budget selection schemes tested were equivalent, so isn't necessary the extra computation of k-means cluster centers.
Online Kernel Matrix Factorization Thesis
By Andres Esteban Paez Torres
Online Kernel Matrix Factorization Thesis
My thesis presentation
