James L. Weaver
Quantum Developer Advocate
james.weaver@ibm.com
JavaFXpert.com
CulturedEar.com
@JavaFXpert
Jamming with a Quantum Computer
Because NISQ* begins with Noisy
*Noisy Intermediate Scale Quantum computers
Browser-based slides:
About Presenter James Weaver
Java Champion, JavaOne Rockstar, plays well with others, etc :-)
Author of several Java/JavaFX/RaspPi books
Quantum Developer Advocate at IBM
Concepts we'll address today
-
Quantum computing overview
-
Relationship between music and quantum computing
-
Species counterpoint musical style
-
Composing music probabilistically
-
Creating melodies and harmonies with quantum notes
- Musical composition and jamming demos along the way
History repeating itself
massive hardware, limited bits, software infancy
Quantum computers make direct use of quantum-mechanical phenomena, such as superposition and entanglement, to perform operations on data.
IBM Announces Q System One at CES 2019
Why use a quantum computer?
Feasible on classical computers
Feasible on quantum computers
Solutions to problems
some problems may be solved exponentially faster
Breaking RSA crypto
someday maybe, using Shor's algorithm
“If you start factoring 10-digit numbers then it’s going to start getting scary”
Dr. Peter Shor, 2013
Related paper published 25 Jan 1997 by Dr. Shor:
Note: Shor's algorithm was formulated in 1994
Quickly searching unsorted data
using Grover's algorithm
"Programming a quantum computer is particularly interesting since there are multiple things happening in the same hardware simultaneously. One needs to think like both a theoretical physicist and a computer scientist."
Dr. Lov Grover, 2002
Related paper published 17 Jul 1997 by Dr. Grover:
Simulating nature
complex chemical reactions, for example
“Nature isn't classical, dammit, and if you want to make a simulation of nature, you'd better make it quantum mechanical, and by golly it's a wonderful problem, because it doesn't look so easy.”
Dr. Richard Feynman, 1981
Near-term quantum computing domains
Conspicuously absent: Music composition & improvisation
Machine Learning
Optimization
Chemistry
Finance
Music and quantum mechanics are probabilistic
"Once a musical style has become part of the habit responses of composers, performers, and practiced listeners it may be regarded as a complex system of probabilities."
- Leonard B. Meyer, Music, the Arts, and Ideas
To inaccurately paraphrase Dr. Feynman...
Bongo music isn't classical, dammit, and if you want to make a simulation of music, you'd better make it quantum mechanical.
The Big Idea:
Ask a quantum computer to compose music
We'll demo a simplified version of the species counterpoint style of music, as it is well defined and may be expressed using probabilities
From OpenMusicTheory.com Composing a second-species counterpoint
What is counterpoint?
The relationship between voices that are interdependent harmonically yet independent in rhythm and contour
Tip: For a gentle introduction to counterpoint, check out the Species Counterpoint article by Nicholas H. Tollervey
From OpenMusicTheory.com Composing a second-species counterpoint
Text
Italian Renaissance composer of sacred music
- Created Palestrina-style counterpoint
- Best known 16th-century representative of the Roman School of musical composition
- Influenced music of composers such as Johann Sebastian Bach
Born in Austria, Johann codified Palestrina's techniques in the 1700s, calling it species-counterpoint, mainly for teaching students.
- Published in Gradus ad Parnassum *
- Describe valid pitch and rhythmic relationships between notes
- Influenced music of Hayden, Mozart and Beethoven
* Steps to Mt. Parnassos (which was the home of the muses)
Quantum Music Composer app
Transition matrix
edition
Expressing melodic characteristics
Example characteristics of counterpoint melodies:
- mostly stepwise motion, but with some leaps (mostly small leaps)
- tendency for melodies to move by descending step more than ascending
in a transition matrix
Expressing harmonic characteristics
Example characteristics of counterpoint harmonies:
- All harmonic consonances are allowed.
- Imperfect consonances are preferable to perfect consonances
- Unisons should only be used for first and last intervals.
in a transition matrix
What's Quantum Got to Do with It?
Volkmar Putz and Karl Svozil, “Quantum music,” (2015), arXiv:1503.09045 [quant-ph]
In Quantum Music Composer, note pitches are represented by quantum states
Melodic and harmonic transitions are realized by quantum logic gates
\vert\space\space\space\rangle
=
\begin{bmatrix}
1 \\
0
\end{bmatrix}
\vert\space\space\space\rangle
=
\begin{bmatrix}
0 \\
1
\end{bmatrix}
=
\begin{bmatrix}
\sqrt{\frac{1}{3}} \\
\sqrt{\frac{2}{3}}
\end{bmatrix}
\sqrt{\frac{1}{3}}
\vert\space\space\space\rangle
+
\sqrt{\frac{2}{3}}
\vert\space\space\space\rangle
\vert\space\space\space\rangle
\vert\space\space\space\rangle
Representing quantum states
\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle
\vert\space\space\space\rangle
Modifying transition matrices
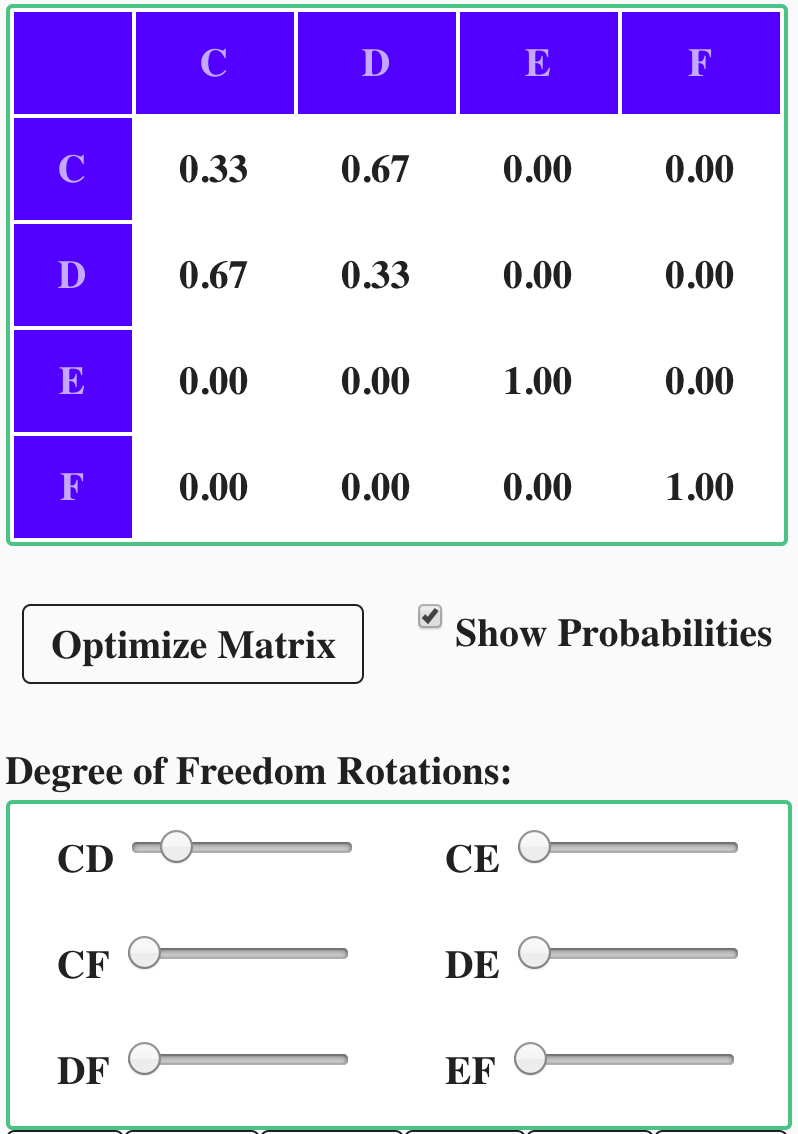
using degree of freedom rotations
.33\approx\frac{1}{3}
.67\approx\frac{2}{3}
.57\approx\sqrt{\frac{1}{3}}
.82\approx\sqrt{\frac{2}{3}}
Quantum computer composing a melody
\vert\space\space\space\rangle
\vert\space\space\space\rangle
\vert\space\space\space\rangle
\vert\space\space\space\rangle
\vert\space\space\space\rangle
\vert\space\space\space\rangle
\frac{1}{3}
\frac{2}{3}
wp
wp
Sample melody:
...
...
Quantum computer composing a song
Quantum Musical Composition from Melbourne
Representing Qubits with the Bloch Sphere
IBM Q Experience
Composing quantum circuits
IBM Q Experience
Quantum Assembly Language (QASM)
IBM Q Experience measurement results
Developing quantum apps
Qiskit open source quantum computing framework
Developing quantum apps
Qiskit Terra foundational stack
Minimal Qiskit example
Sample output:
{'00': 496, '11': 528}
Expresses circuit:
Composing in the Bell states
\sqrt{\frac{1}{2}}
\vert\space\space\space\rangle
+
\sqrt{\frac{1}{2}}
\vert\space\space\space\rangle
00
C
11
F
\sqrt{\frac{1}{2}}
\vert\space\space\space\rangle
-
\sqrt{\frac{1}{2}}
\vert\space\space\space\rangle
01
D
10
E
\sqrt{\frac{1}{2}}
\vert\space\space\space\rangle
-
\sqrt{\frac{1}{2}}
\vert\space\space\space\rangle
00
C
11
F
\sqrt{\frac{1}{2}}
\vert\space\space\space\rangle
+
\sqrt{\frac{1}{2}}
\vert\space\space\space\rangle
01
D
10
E
Developing quantum apps
Qiskit Aqua quantum algorithms
Near-term quantum computing domains
Conspicuously absent: Music composition & improvisation
Machine Learning
Optimization
Chemistry
Finance
Close encounters of the minor third kind
Hands-on Qiskit workshop
Now it's your turn to play!
Instructions are in my Learning Qiskit: Guided exercises for developers project on GitHub
Jamming with a Quantum Computer
{\frac{1}{\sqrt2}}
\vert{Q}\rangle
+
\vert{A}\rangle
{\frac{1}{\sqrt2}}
Because NISQ begins with Noisy
James L. Weaver
Quantum Developer Advocate
james.weaver@ibm.com
JavaFXpert.com
CulturedEar.com
@JavaFXpert
Jamming with a Quantum Computer
By javafxpert
Jamming with a Quantum Computer
Because NISQ begins with Noisy
