Neural Field Transformations

(for lattice gauge theory)

Sam Foreman

2021-03-11

Introduction

  • LatticeQCD:

    • Non-perturbative approach to solving the QCD theory of the strong interaction between quarks and gluons

  • Calculations in LatticeQCD proceed in 3 steps:

  • Gauge field generation: Use Markov Chain Monte Carlo (MCMC) methods for sampling independent gauge field (gluon) configurations.
  • ​Propagator calculations: Compute how quarks propagate in these fields ("quark propagators")
  • Contractions: Method for combining quark propagators into correlation functions and observables.

Motivation: Lattice QCD

  • Generating independent gauge configurations is a major bottleneck in the HEP/LatticeQCD workflow
  • As the lattice spacing \(a\rightarrow 0\), configurations get stuck

stuck

\(a\)

continuum limit

Markov Chain Monte Carlo (MCMC)

  • Goal: Draw independent samples from a target distribution, \(p(x)\)
x^{\prime} = x_{0} + \delta,\quad \delta\sim\mathcal{N}(0, \mathbb{1})
  • Starting from some initial state \(x_{0}\) (randomly chosen), we generate proposal configurations \(x^{\prime}\)
  • Use Metropolis-Hastings acceptance criteria
x_{i+1} = \begin{cases} x^{\prime},\quad\text{with probability } A(x^{\prime}|x)\\ x,\quad\text{with probability } 1 - A(x^{\prime}|x) \end{cases}
A(x^{\prime}|x) = \min\left\{1, \frac{p(x^{\prime})}{p(x)}\left|\frac{\partial x^{\prime}}{\partial x^{T}}\right|\right\}

Metropolis-Hastings: Accept/Reject

import numpy as np

def metropolis_hastings(p, steps=1000):
    x = 0.                   # initialize config
    samples = np.zeros(steps)
    for i in range(steps):
        x_prime = x + np.random.randn()           # proposed config
        if np.random.rand() < p(x_prime) / p(x):  # compute A(x'|x)
            x = x_prime      # accept proposed config
        samples[i] = x       # accumulate configs 
    
    return samples
N \longrightarrow \infty

As

x\sim p

,

Issues with MCMC

  • Generate proposal configurations

dropped configurations

Inefficient!

\{x_{0}, x_{1}, x_{2}, \ldots, x_{k}, x_{k+1}, x_{k+2}, x_{k+3}, \ldots, x_{m}, x_{m+1}, x_{m+2}, \ldots, x_{n-2}, x_{n-1}, x_{n}\}
  • Construct chain:
  • Account for thermalization ("burn-in"):
\{x_{0}, x_{1}, x_{2}, \ldots, x_{k}, x_{k+1}, x_{k+2}, x_{k+3}, \ldots, x_{m}, x_{m+1}, x_{m+2}, \ldots, x_{n-2}, x_{n-1}, x_{n}\}
  • Account for correlations between states ("thinning"):
\{x_{0}, x_{1}, x_{2}, \ldots, x_{k}, x_{k+1}, x_{k+2}, x_{k+3}, \ldots, x_{m}, x_{m+1}, x_{m+2}, \ldots, x_{n-2}, x_{n-1}, x_{n}\}
x^{\prime} = x + \delta, \quad\text{where}\quad \delta \sim \mathcal{N}(0, \mathbb{1})

Hamiltonian Monte Carlo (HMC)

  • Target distribution:

\(p(x)\propto e^{-S(x)}\)

  • Introduce fictitious momentum:

 

  • Joint target distribution, \(p(x, v)\)

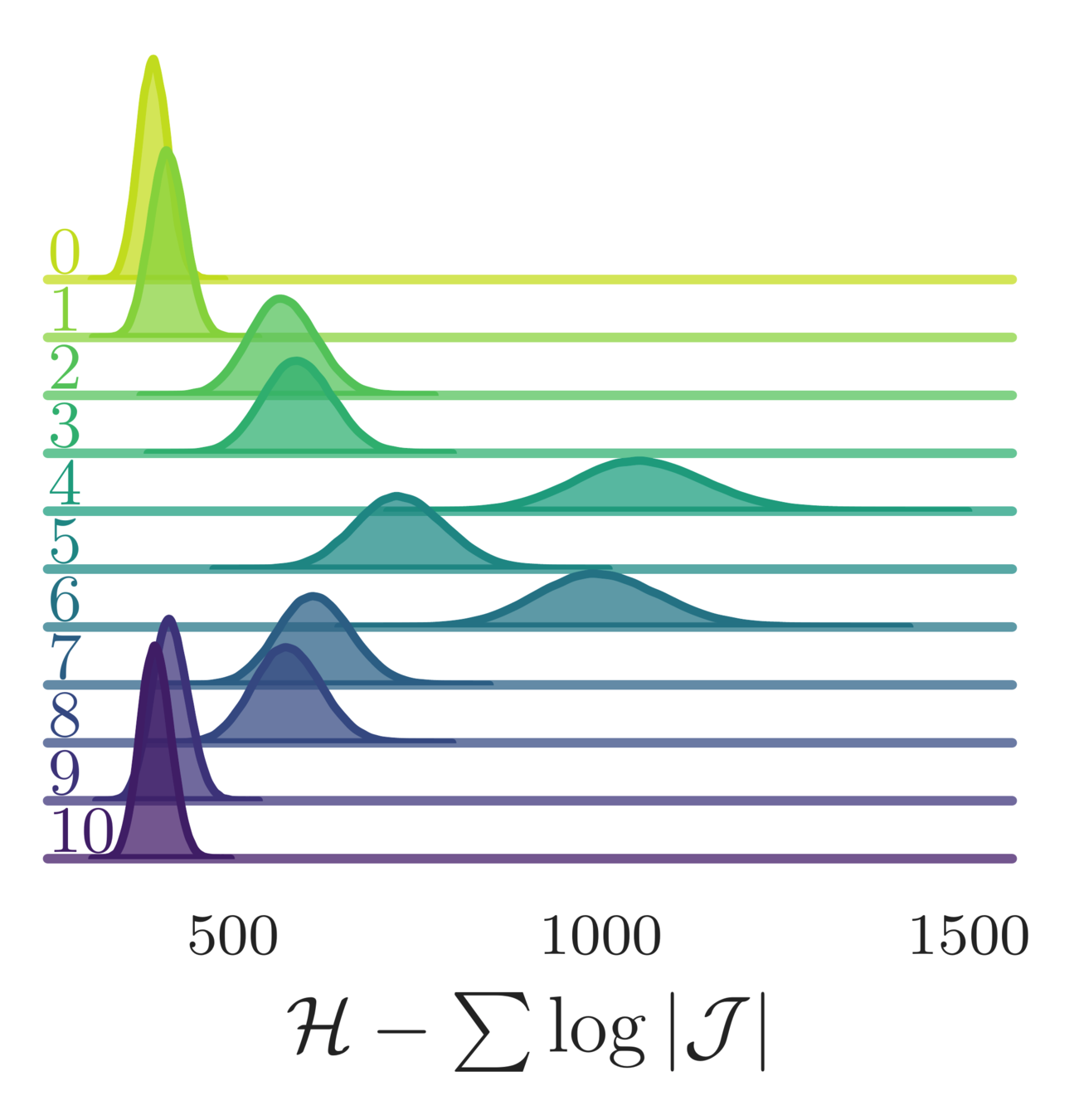
\(p(x, v) = p(x)\cdot p(v) = e^{-S(x)}\cdot e^{-\frac{1}{2}v^{T}v} = e^{-\mathcal{H(x,v)}}\)

  • The joint \((x, v)\) system obeys Hamilton's Equations:

\(v\sim\mathcal{N}(0, 1)\)

\(\dot{x} = \frac{\partial\mathcal{H}}{\partial v}\)

\(\dot{v} = -\frac{\partial\mathcal{H}}{\partial x}\)

\(S(x)\) is the action

(potential energy)

HMC: Leapfrog Integrator

 \(\dot{v}=-\frac{\partial\mathcal{H}}{\partial x}\) 

\(\dot{x}=\frac{\partial\mathcal{H}}{\partial v}\)

Hamilton's Equations:

v^{1/2} = v - \frac{\varepsilon}{2}\partial_{x}S(x)
x^{\prime} = x + \varepsilon v^{1/2}
v^{\prime} = v^{1/2} - \frac{\varepsilon}{2}\partial_{x}S(x^{\prime})

2. Full-step position update:

1. Half-step momentum update:

3. Half-step momentum update:

\mathcal{H}(x, v) = S(x) + \frac{1}{2}v^{T}v \Longrightarrow

HMC: Issues

  • Cannot easily traverse low-density zones.

    • ​\(A(\xi^{\prime}|\xi)\approx 0\)

  • What do we want in a good sampler?

  • Fast mixing
  • Fast burn-in
  • Mix across energy levels
  • Mix between modes

  • Energy levels selected randomly

    • \(v\sim \mathcal{N}(0, 1)\) \(\longrightarrow\) slow mixing!

(especially for Lattice QCD)

L2HMC: Generalized Leapfrog

  • Main idea: 
    • Introduce six auxiliary functions, \((s_{x}, t_{x}, q_{x})\), \((s_{v}, t_{v}, q_{v})\) into the leapfrog updates, which are parameterized by weights \(\theta\) in a neural network.
  • Notation:
    • ​Introduce a binary direction variable, \(d\sim\mathcal{U}(+,-)\)
      • ​distributed independently of \(x\), \(v\)
    • Denote a complete state by \(\xi = (x, v, d)\), with target distribution \(p(\xi)\):
= p(x, v, d) = p(x)\cdot p(v)\cdot p(d)
p(\xi)

L2HMC: Generalized Leapfrog

v^{\prime}_{k} \equiv \Gamma^{+}_{k}(v_{k};\zeta_{v_{k}}) = v_{k}\odot \exp\left(\frac{\varepsilon^{k}_{v}}{2}s^{k}_{v}(\zeta_{v_{k}})\right) - \frac{\varepsilon^{k}_{v}}{2}\left[\partial_{x}S(x_{k})\odot\exp\left(\varepsilon^{k}_{v}q^{k}_{v}(\zeta_{v_{k}})\right) + t^{k}_{v}(\zeta_{v_{k}})\right]
\overbrace{\hspace{85px}}

Momentum scaling

Gradient scaling

\overbrace{\hspace{30px}}

Translation

x^{\prime}_{k} \equiv \Lambda^{+}_{k}(x_{k};\zeta_{x_{k}}) = x_{k}\odot\exp\left(\varepsilon^{k}_{x}s^{k}_{x}(\zeta_{x_{k}})\right) + \varepsilon^{k}_{x}\left[v^{\prime}_{k}\odot\exp\left(\varepsilon^{k}_{x}q^{k}_{x}(\zeta_{x_{k}})\right)+t^{k}_{x}(\zeta_{x_{k}})\right]
\overbrace{\hspace{105px}}

momentum

position

  • Introduce generalized \(v\)-update, \(v^{\prime}_{k} = \Gamma^{+}_{k}(v_{k};\zeta_{v_{k}})\):

with \(\zeta_{x_{k}} = (x_{k}, v_{k}, \tau(k))\)

  • And the generalized \(x\)-update, \(x^{\prime}_{k} = \Lambda^{+}_{k}(x_{k};\zeta_{x_{k}})\)

with (\(v\)-independent) \(\zeta_{v_{k}} \equiv (x_{k}, \partial_{x}S(x_{k}), \tau(k))\)​

L2HMC: Generalized Leapfrog

  • Complete (generalized) update:
    1. Half-step momentum update:
    2. Full-step half-position update:
    3. Full-step half-position update:
    4. Half-step momentum update:
v^{\prime}_{k} = \Gamma^{\pm}_{k}(v_{k};\zeta_{v_{k}})
x^{\prime}_{k} = \hspace{14px}\odot\, x_{k} + \hspace{14px}\odot\, \Lambda^{\pm}_{k}(x_{k};\zeta_{x_{k}})
\bar{m}^{t}
m^{t}
v^{\prime\prime}_{k} = \Gamma^{\pm}_{k}(v^{\prime}_{k};\zeta_{v^{\prime}_{k}})
\bar{m}^{t}
m^{t}
=\mathbb{1}
+

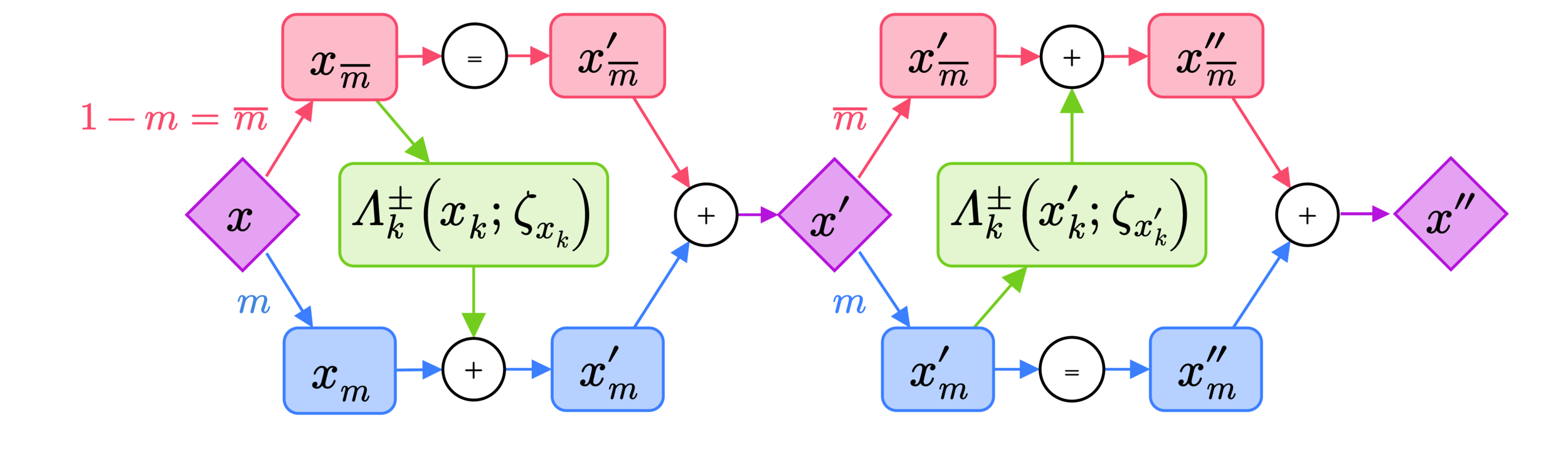
Note:

split via \(m^t\)

x^{\prime\prime}_{k} = \hspace{14px}\odot\, \Lambda^{\pm}_{k}(x^{\prime}_{k};\zeta_{x^{\prime}_{k}}) + \hspace{14px}\odot\, x^{\prime}_{k}
\bar{m}^{t}
m^{t}

Network Architecture

s_{x} = \alpha_{s}\tanh(w^{T}_{s} h_{n} + b_{s})
q_{x} = \alpha_{q}\tanh(w^{T}_{q} h_{n} + b_{q})
t_{x} = w_{t}^{T} h_{n} + b_{t}

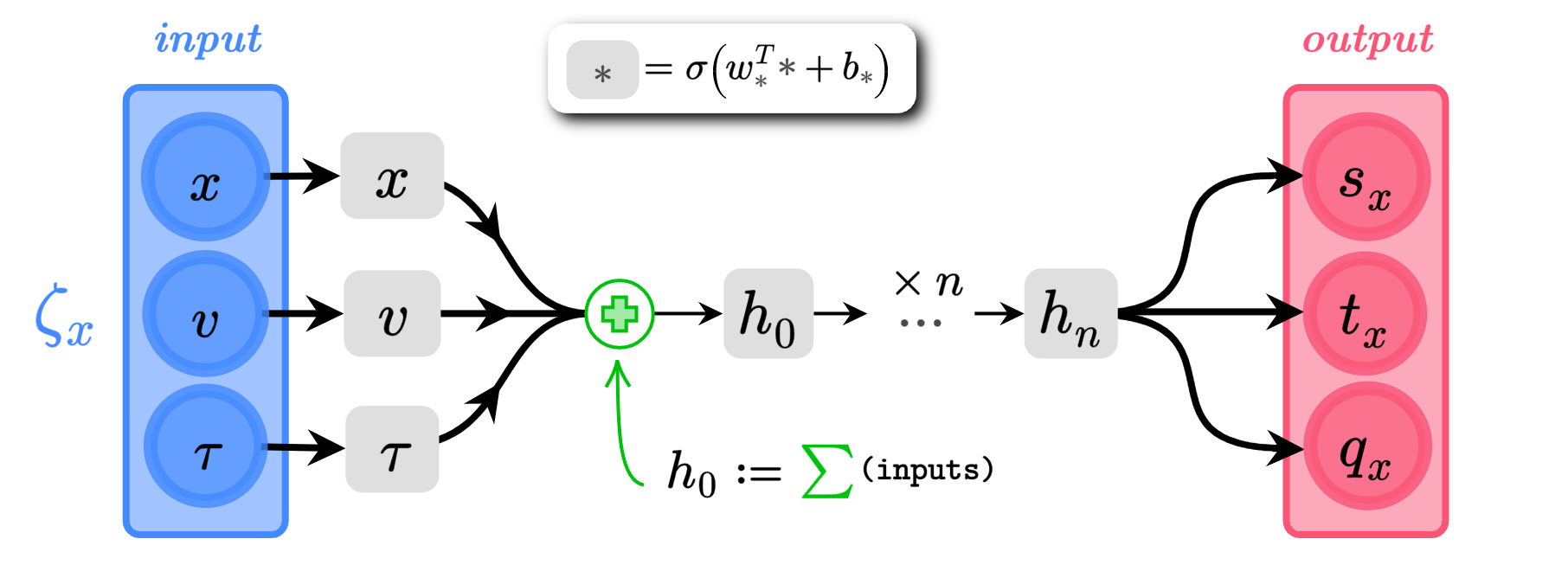
(\(\alpha_{s}, \alpha_{q}\) are trainable parameters)

\(x\), \(v\) \(\in \mathbb{R}^{d}\)

\(s_{x}\),\(q_{x}\),\(t_{x}\) \(\in \mathbb{R}^{d}\)

Loss function, \(\mathcal{L}(\theta)\)

  • Goal: Maximize "expected squared jump distance" (ESJD), \(A(\xi^{\prime}|\xi)\cdot \delta(\xi^{\prime}, \xi)\):
\ell_{\theta}\left[\xi^{\prime}, \xi, A(\xi^{\prime}|\xi)\right] = \frac{a^{2}}{A(\xi^{\prime}|\xi)\cdot\delta(\xi^{\prime},\xi)} - \frac{A(\xi^{\prime}|\xi)\cdot\delta(\xi^{\prime},\xi)}{a^{2}}
\delta(\xi^{\prime}, \xi) = \|x^{\prime} - x\|^{2}_{2}
  • Define the "squared jump distance":
\mathcal{L}_{\theta}\left(\theta\right) \equiv \mathbb{E}_{p(\xi)}\left[\ell_{\theta}\right]

where:

L2HMC

HMC

GMM: Autocorrelation

Annealing Schedule

\left\{\gamma_{t}\right\}_{t=0}^{N} = \left\{\gamma_{0}, \gamma_{1}, \ldots, \gamma_{N-1}, \gamma_{N}\right\},
\gamma_{0} < \gamma_{1} < \ldots < \gamma_{N} \equiv 1
\gamma_{t+1} - \gamma_{t} \ll 1
p_{t}(x)\propto e^{-\gamma_{t}S(x)},\quad\text{for}\quad t=0, 1,\ldots, N
  • Introduce an annealing schedule during the training phase:
  • For \(\|\gamma_{t}\| < 1\), this helps to rescale (shrink) the energy barriers between isolated modes
    • Allows our sampler to explore previously inaccessible regions of the target distribution
  • Target distribution becomes:

(varied slowly)

 \(= \{0.1, 0.2, \ldots, 0.9, 1.0\}\)

(increasing)

Lattice Gauge Theory

  • Link variables:
U_{\mu}(x) = e^{i\varphi_{\mu}(x)} \in U(1)
\varphi_{\mu}(x) \in [-\pi,\pi]
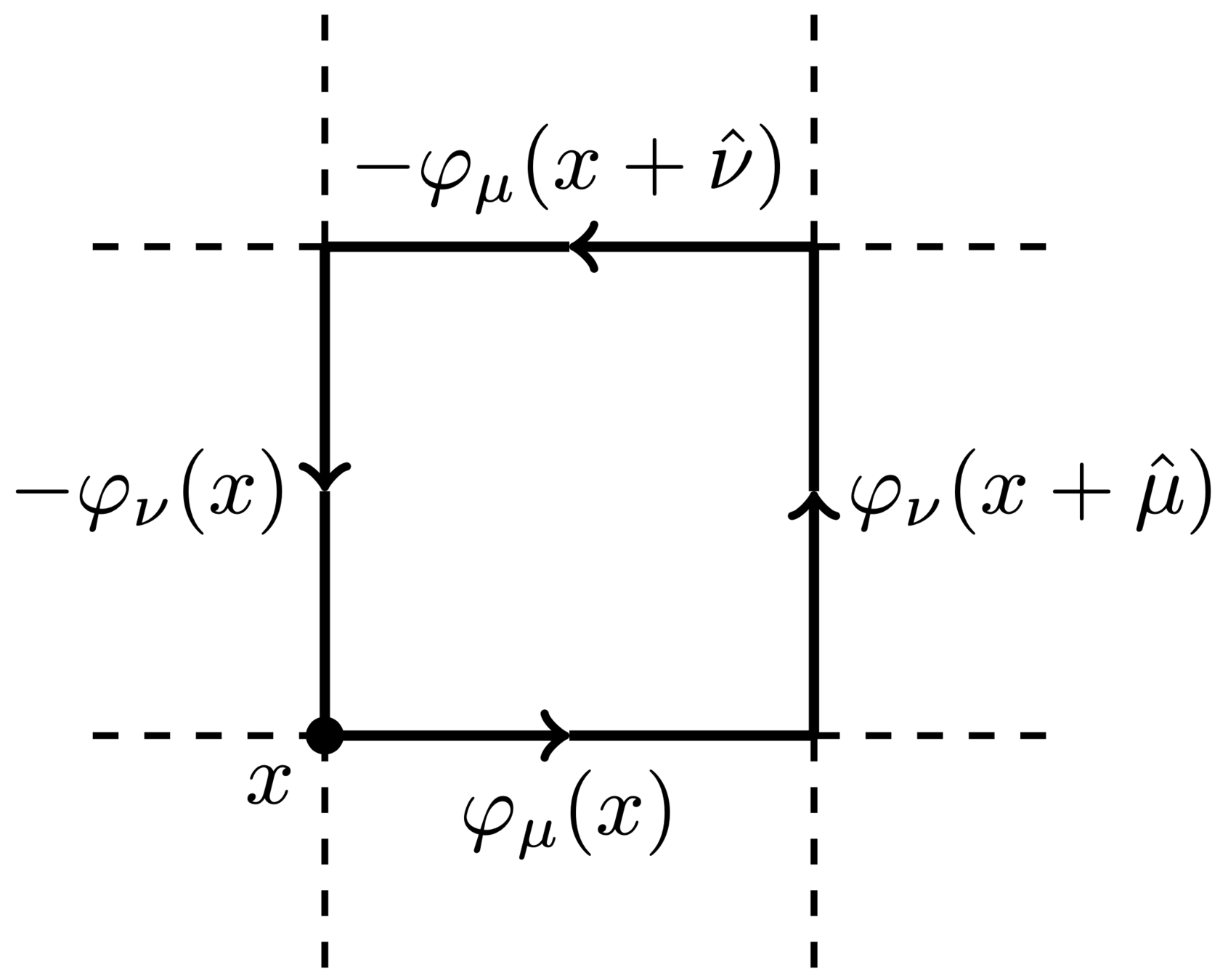
  • Wilson action:
S(\varphi)=\sum_{P}1-\cos\varphi_{P}
\varphi_{P} = \varphi_{\mu}(x) + \varphi_{\nu}(x+\hat{\mu}) - \varphi_{\mu}(x+\hat{\nu}) - \varphi_{\nu}(x)
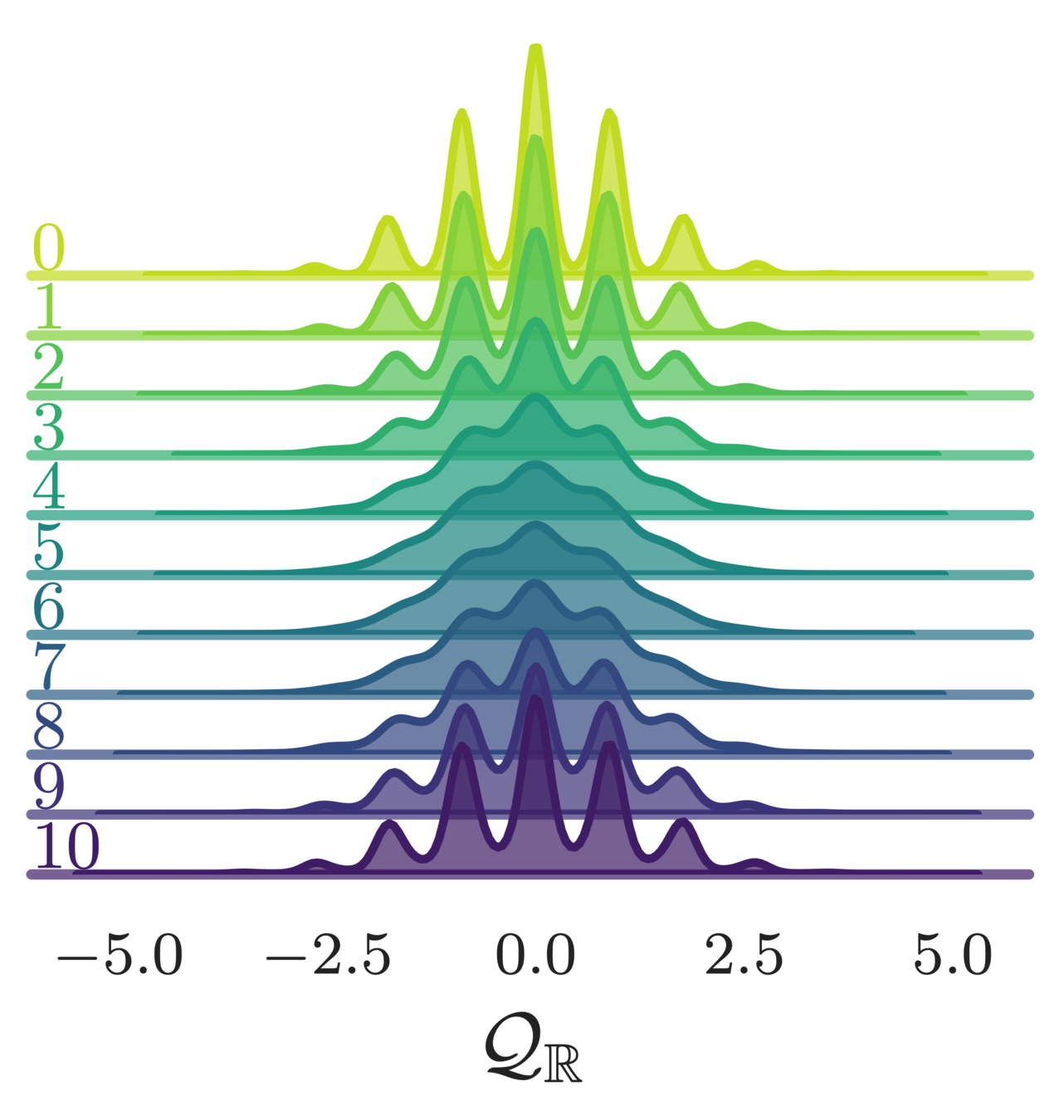
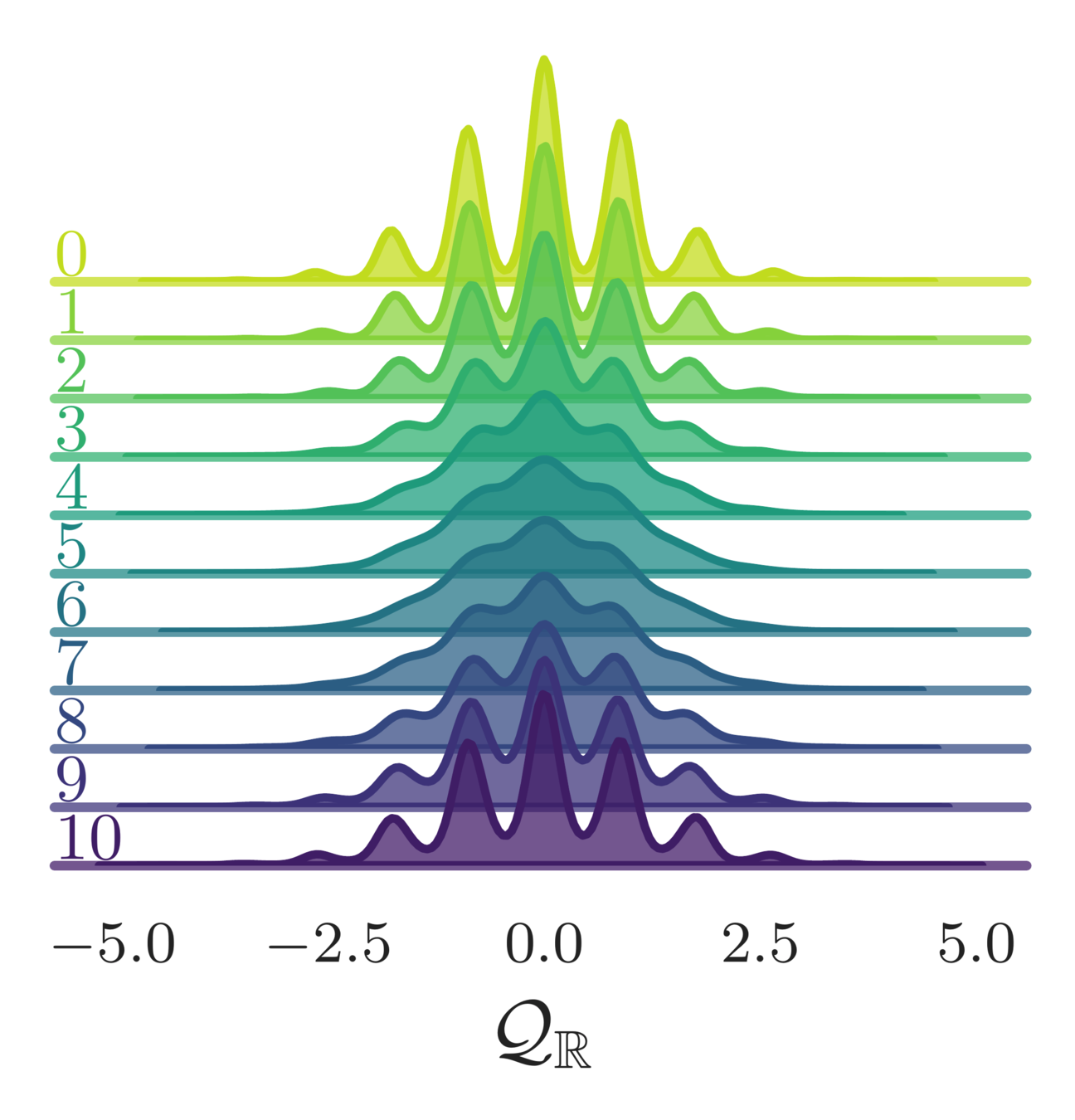
  • Topological charge:
\mathcal{Q}_{\mathbb{Z}} = \frac{1}{2\pi}\sum_{P}\left\lfloor\varphi_{P}\right\rfloor \in\mathbb{Z},
\left\lfloor\varphi_{P}\right\rfloor = \varphi_{P} - 2\pi\left\lfloor\frac{\varphi_{P}+\pi}{2\pi}\right\rfloor
\mathcal{Q}_{\mathbb{R}} = \frac{1}{2\pi}\sum_{P}\sin\varphi_{P}\in\mathbb{R}

(real-valued) 

(integer-valued)

Lattice Gauge Theory

  • Topological Loss Function:
\ell_{\theta}(\xi^{\prime}, \xi, A(\xi^{\prime}|\xi)) = -\frac{1}{a^{2}}A(\xi^{\prime}|\xi)\cdot \delta_{\mathcal{Q}_{\mathbb{R}}}(\xi^{\prime}, \xi)
\delta_{\mathcal{Q}_{\mathbb{R}}}(\xi^{\prime}, \xi) \equiv \left(\mathcal{Q}_{\mathbb{R}}^{\prime} - \mathcal{Q}_{\mathbb{R}}\right)^{2}
= \left(\mathcal{Q}_{\mathbb{R}}(\xi^{\prime}) - \mathcal{Q}_{\mathbb{R}}(\xi)\right)^{2}

\(A(\xi^{\prime}|\xi) = \) "acceptance probability"

where:

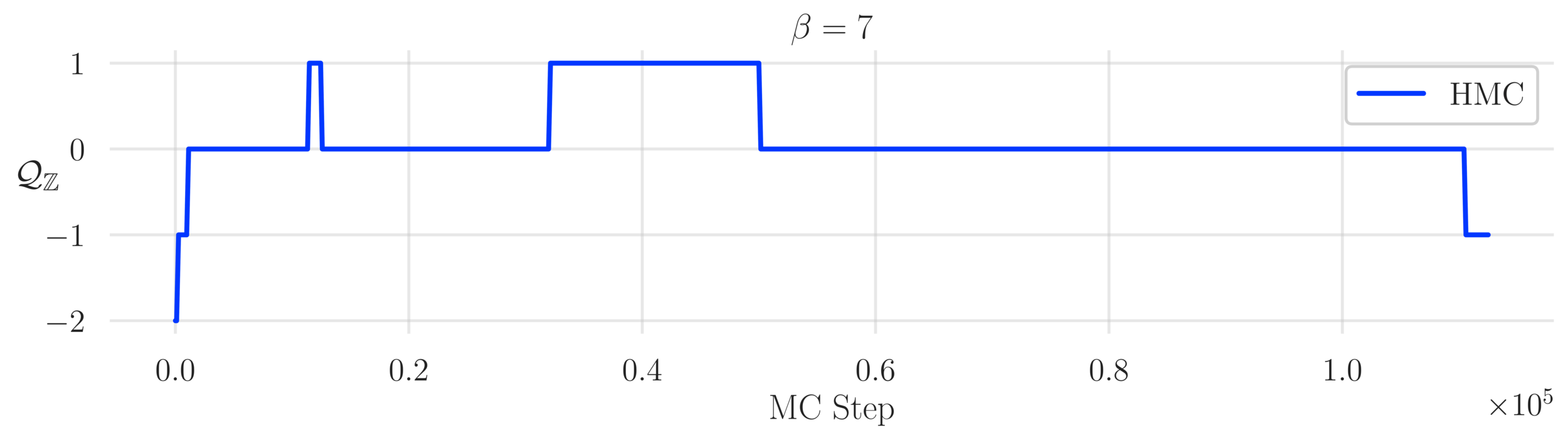
Topological charge history

~ cost / step

continuum limit

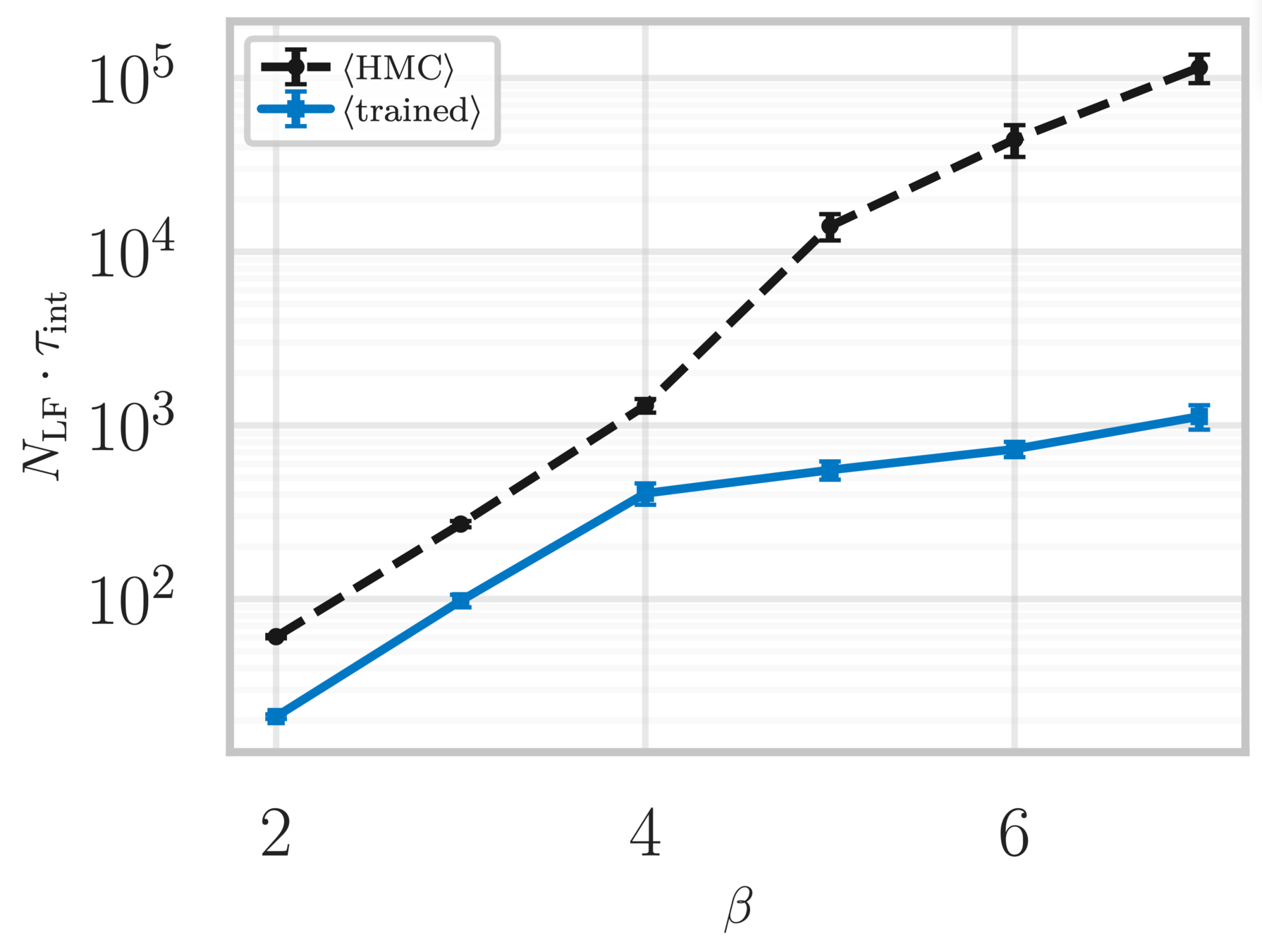
Estimate of the Integrated autocorrelation time of \(\mathcal{Q}_{\mathbb{R}}\)

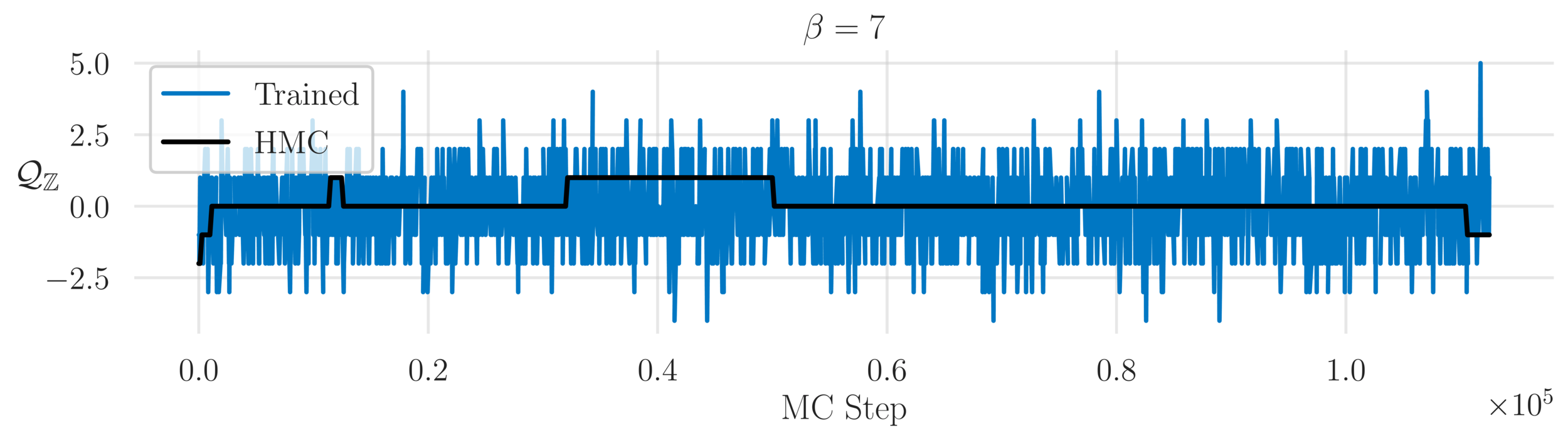
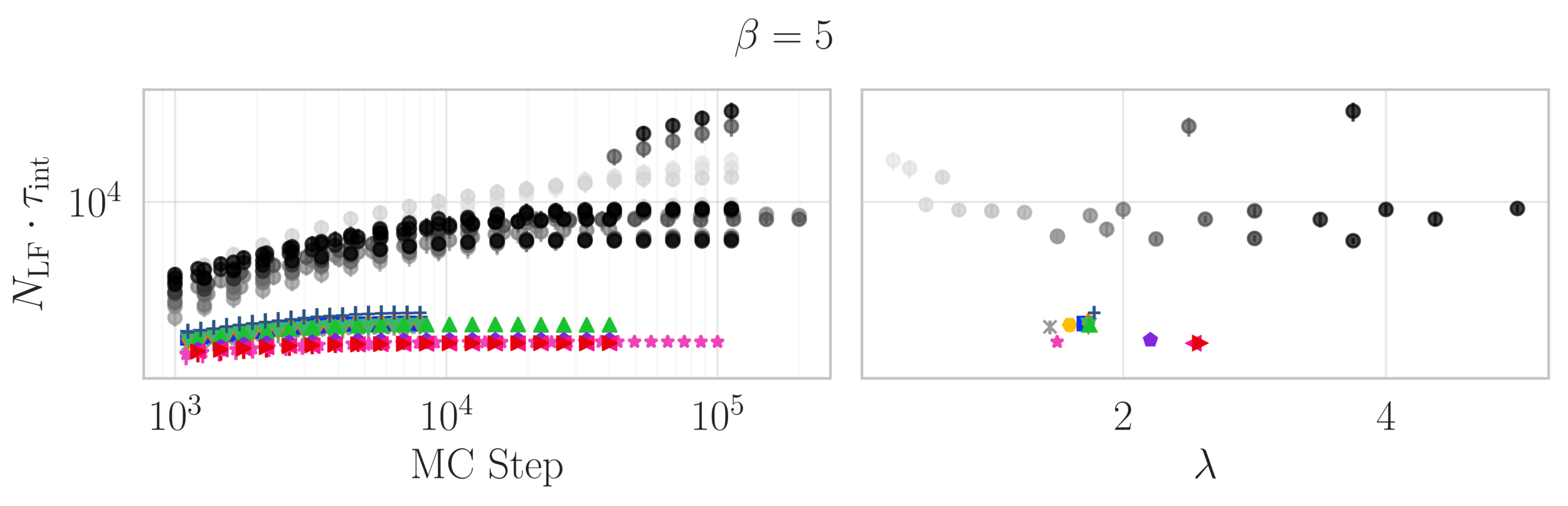
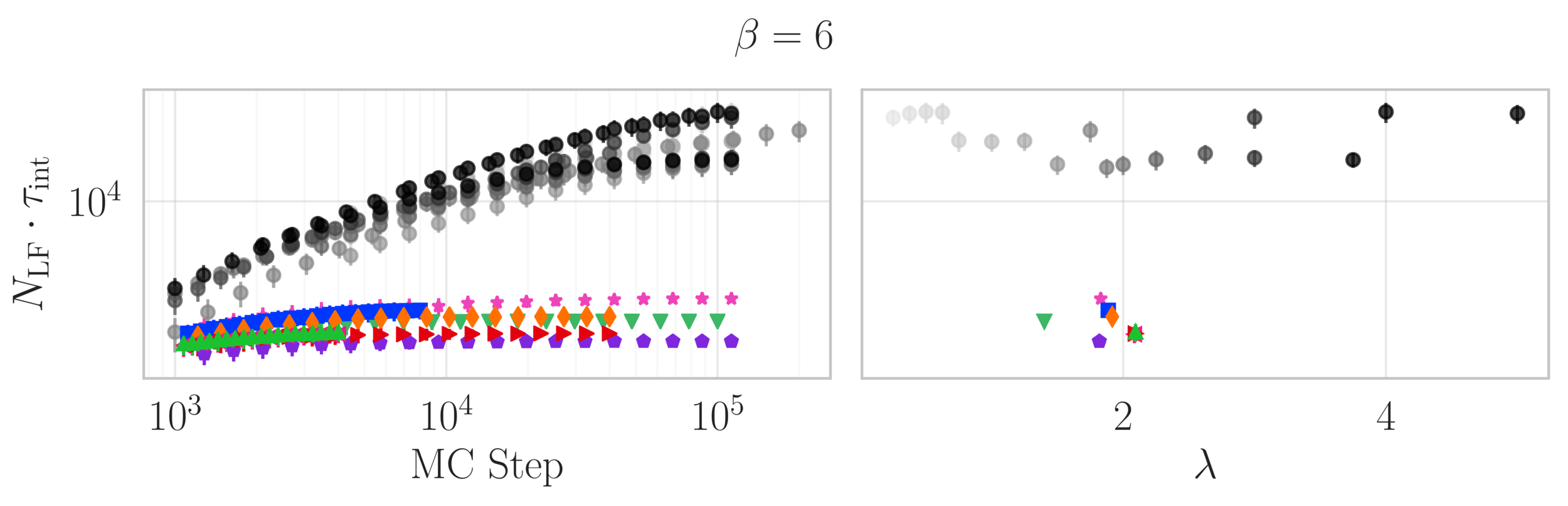
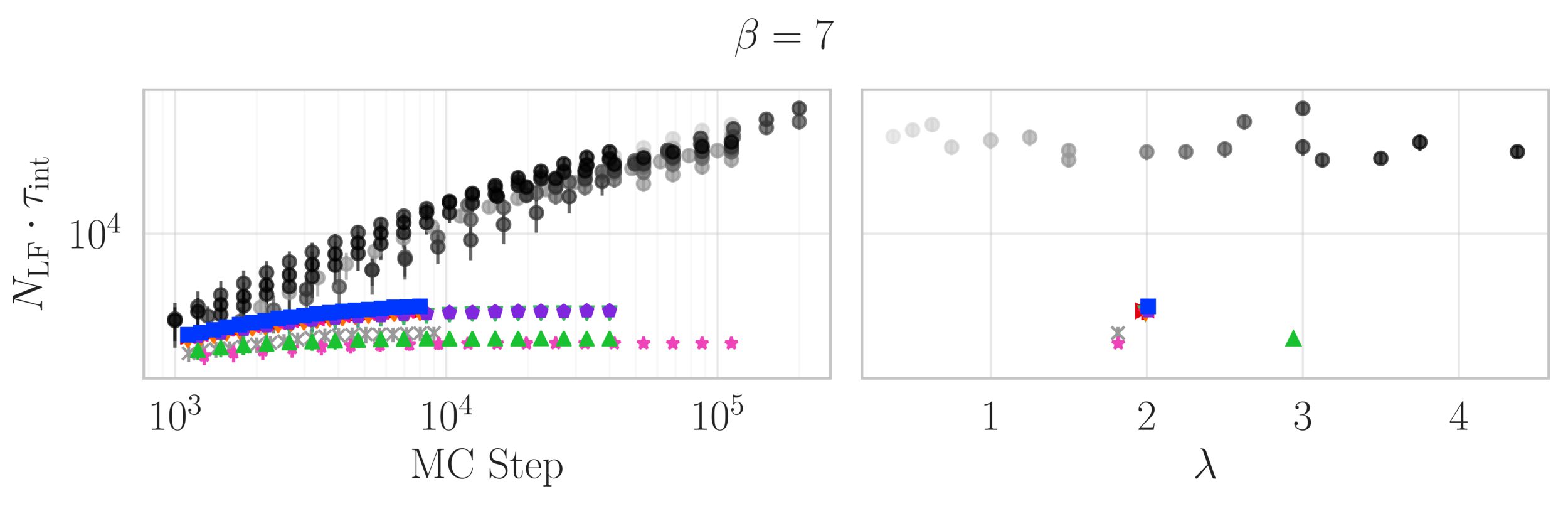
L2HMC

HMC

Lattice Gauge Theory

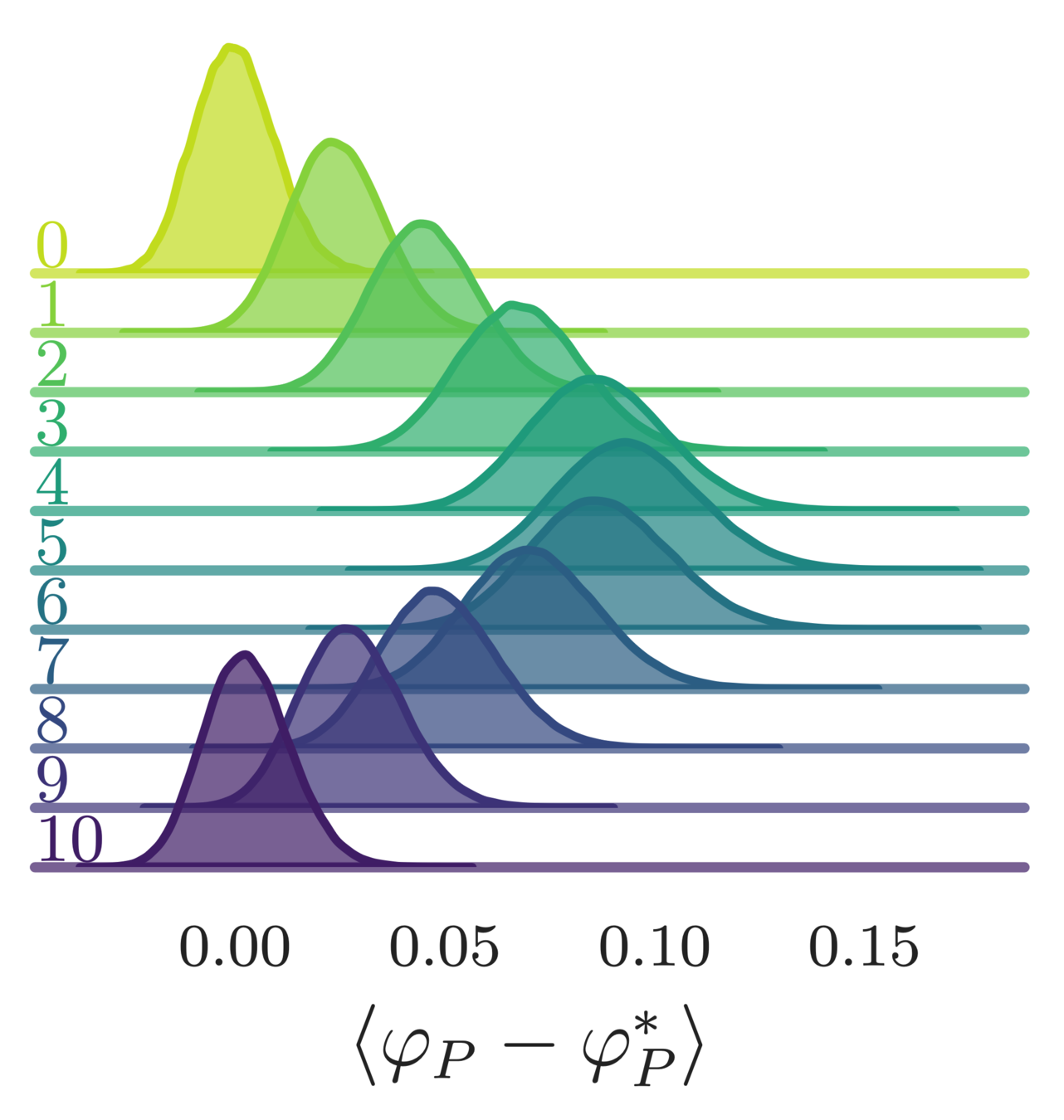
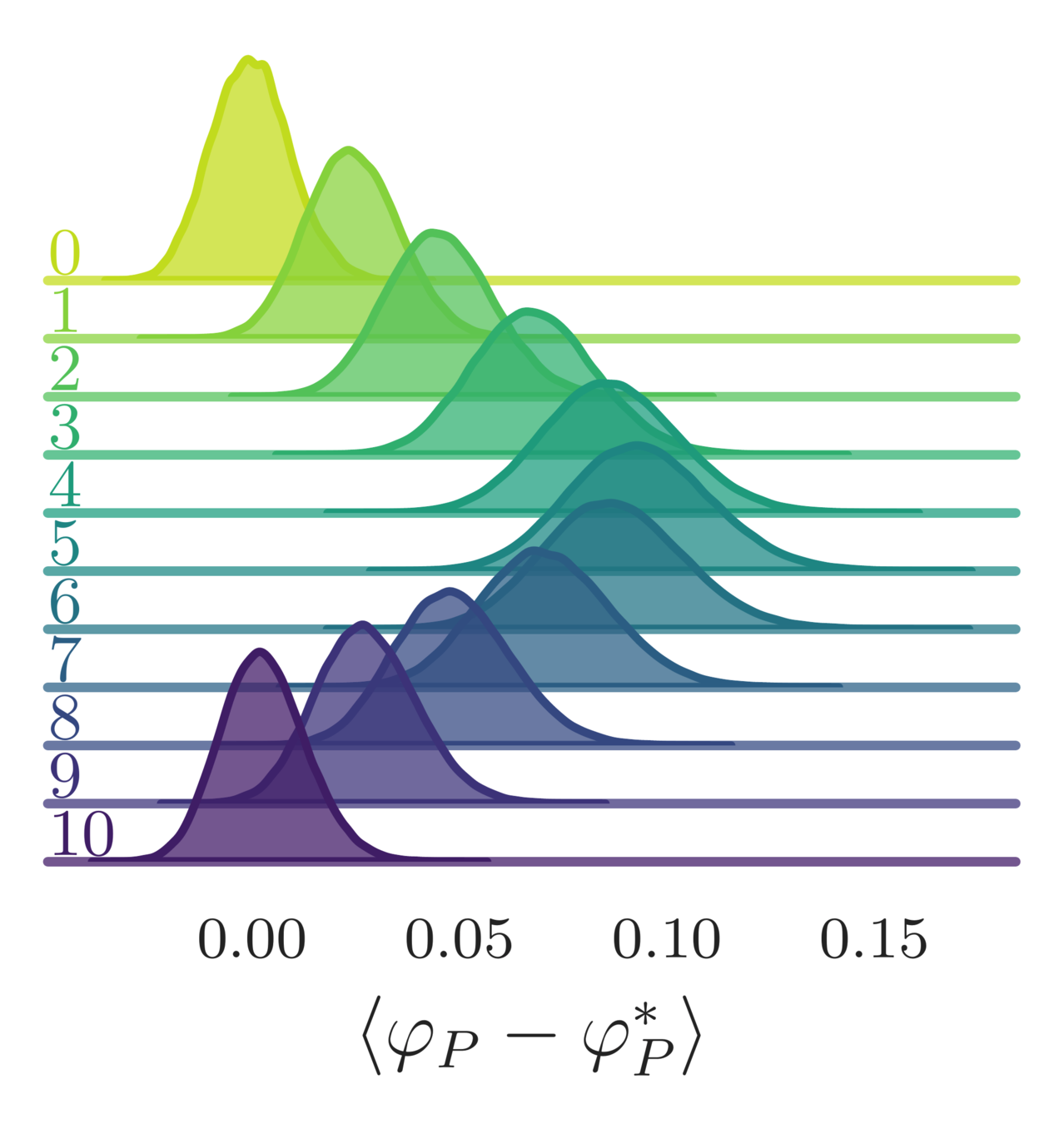
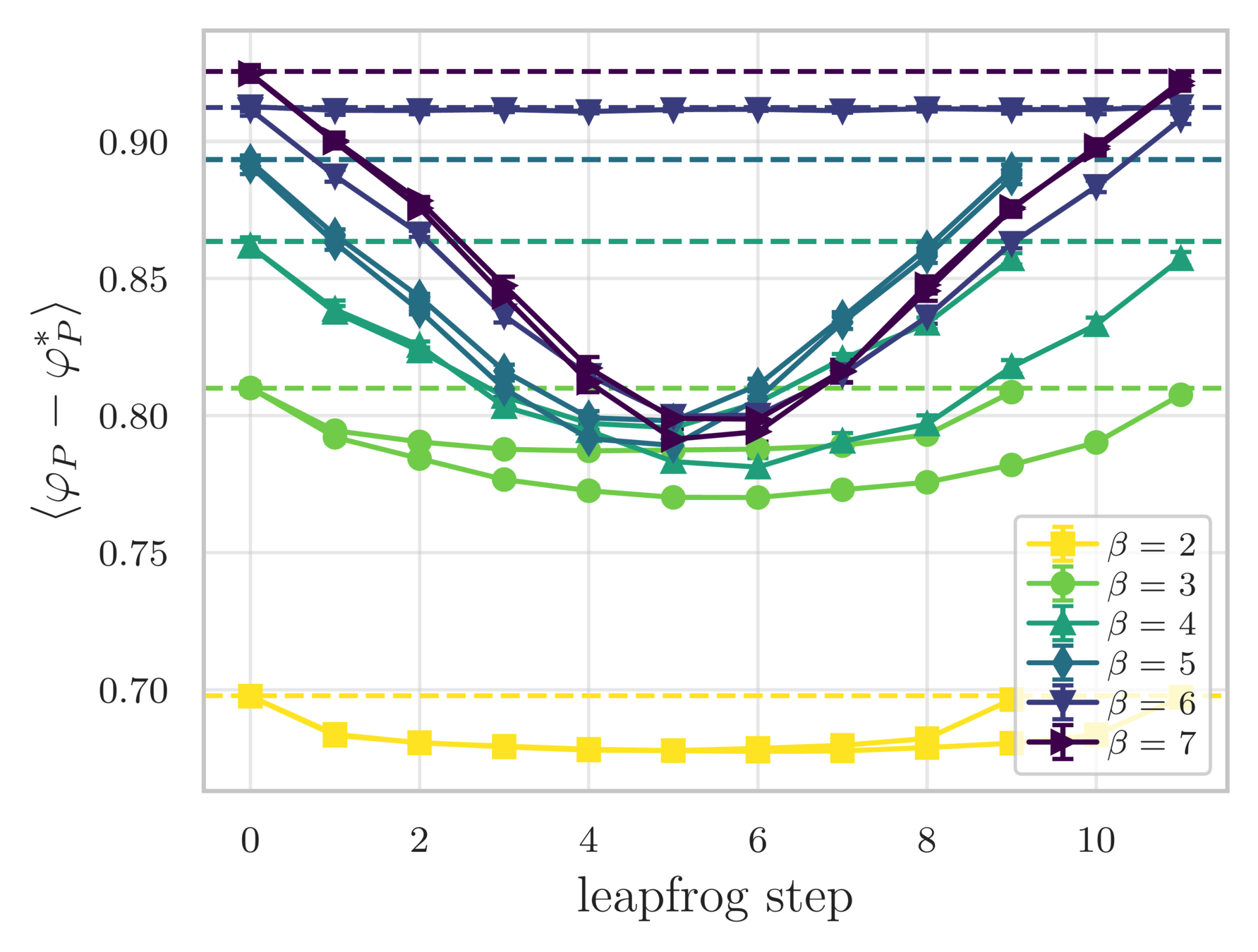
  • Error in the average plaquette, \(\langle\varphi_{P}-\varphi^{*}_{P}\rangle\)
    • where \(\varphi^{*}_{P} = I_{1}(\beta)/I_{0}(\beta)\) is the exact (\(\infty\)-volume) result

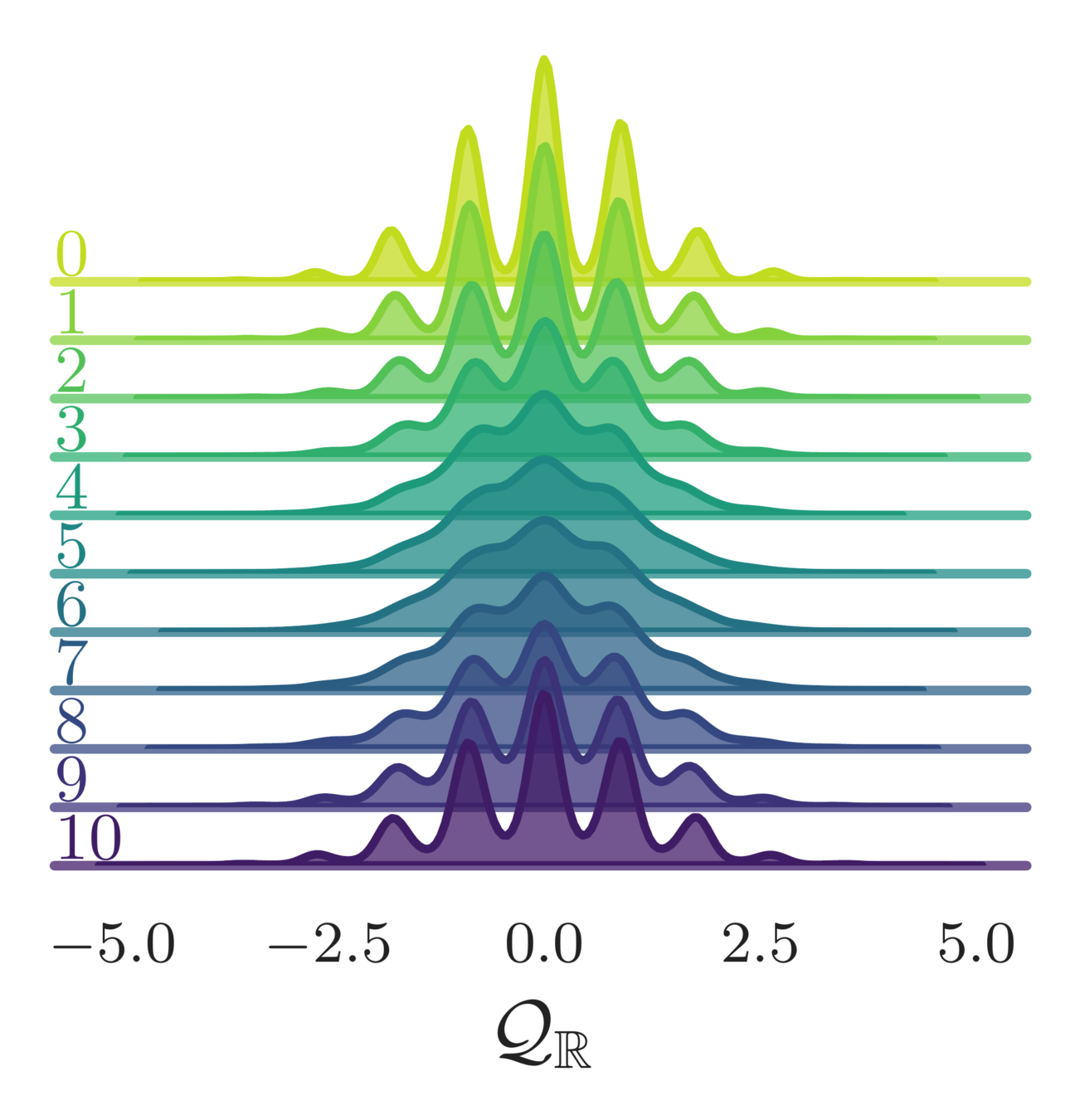
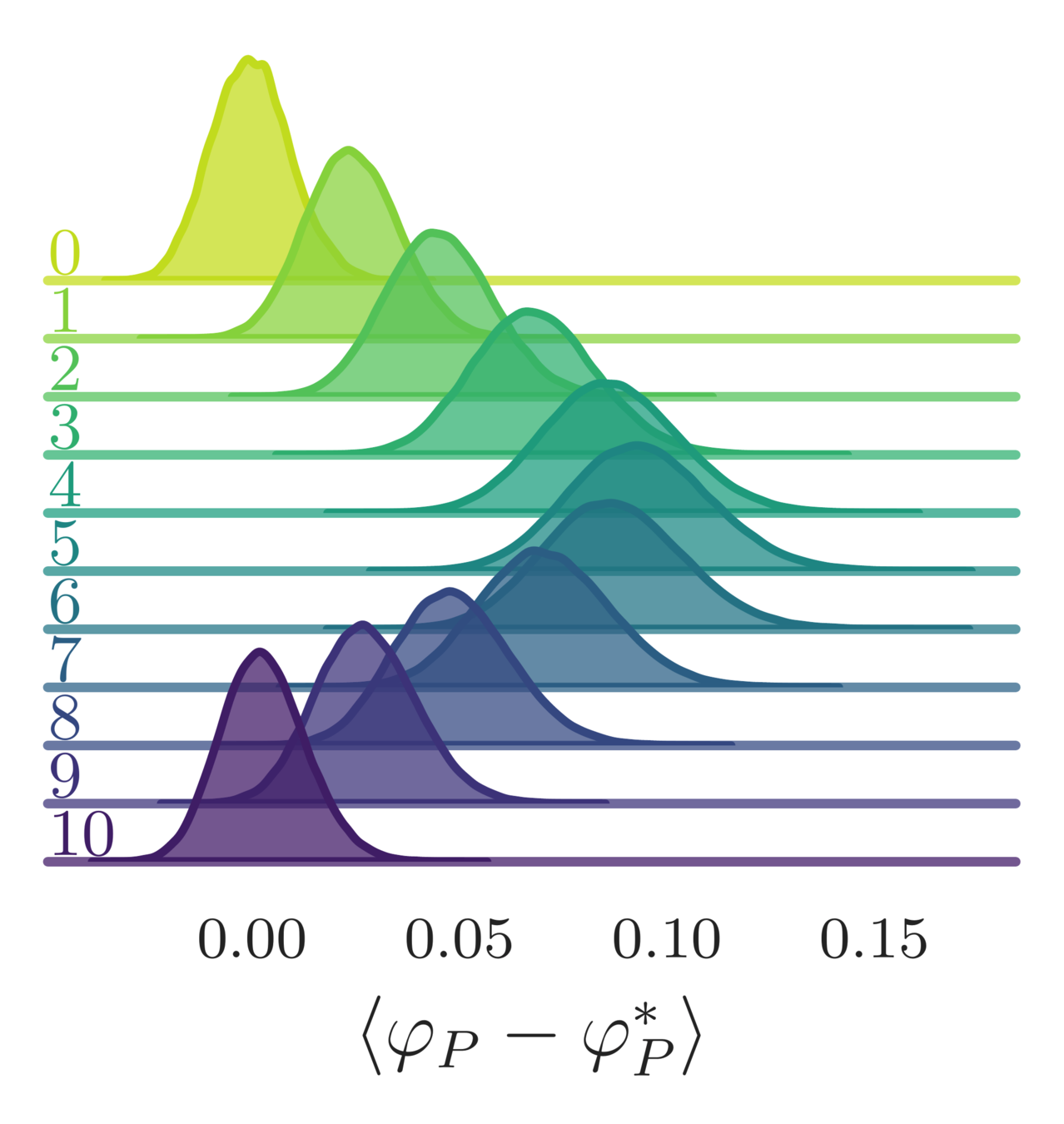
leapfrog step

(MD trajectory)

4096

8192

1024

2048

512

Scaling test: Training

\(4096 \sim 1.73\times\)

\(8192 \sim 2.19\times\)

\(1024 \sim 1.04\times\)

\(2048 \sim 1.29\times\)

\(512\sim 1\times\)

\(4096 \sim 1.73\times\)

\(8192 \sim 2.19\times\)

\(1024 \sim 1.04\times\)

\(2048 \sim 1.29\times\)

\(512\sim 1\times\)

Scaling test: Training

Scaling test: Training

\(8192\sim \times\)

4096

1024

2048

512

Scaling test: Inference

github.com/saforem2/l2hmc-qcd

Thanks!

l2hmc-qcd

By Sam Foreman

Made with Slides.com

l2hmc-qcd

L2HMC algorithm applied to simulations in Lattice QCD

  • 59

More from Sam Foreman