A whirlwind tour of Data Science

Steve Ash
@steve_ash

manycupsofcoffee.com

About Me

  • BA, MS, PhD (almost) Computer Science
  • 10 years building banking and healthcare software
  • 5 years leading "skunkworks" R&D team
  • Poor speller (relevant)

What's this talk?

  • Broad, shallow tour of data science tasks and methods
  • Intuition, not math*
  • Biased to a computer science pov
    • Sorry statisticians, physicists, signal processing folk
  • Necessarily incomplete

* ok it turns out there is a little math

What's a Data Science?

  • No pedantic definitions here, but themes:
  • Tools to extract meaning from lots of data
  • Explore structure and relationships in data
  • Multi-disciplinary, yay!
    • Statistics
    • Computer Science
    • Electrical/Computer Engineering
    • Econometrics
  • Multi-disciplinary, boo!
    • Different names for same thing
    • Math notation, conventions

Data Science

Data Mining

Machine Learning

Predictive Analytics

Artificial Intelligence

Knowledge Discovery

Obligatory Graphics

Tour Outline

  • Process
  • Exploration
    • Single points of data
    • Structure of data
  • Modelling themes
  • Task Families
  • Method families
  • Learning, Optimization
  • Now the bad news

It's an iterative process

  1. Problem definition - who cares about this?
  2. Data preparation - easy systematic access
  3. Data exploration - signal vs noise, patterns
  4. Modelling - noisy inputs -> something useful
  5. Evaluation - what is good?
  6. Deployment - from science to end users

Exploration

Data Exploration

  • Data types
    • Discrete: Categorical: Red, Blue,...
    • Continuous: Numerical: [0, 1], x > 0
  • Exploring single attributes
    • Mean, Variance
    • Skew, Kurtosis
    • Mode

Data Exploration

  • Exploring Single Values (cont)
    • Median, quantiles, box-plots
    • Histograms
       
  • Exploring Pairs of Values
    • Co-variance - how two attributes change together
    • Pearson correlation coefficient - how two attributes change together vs how change individually
    • t/z-test, ANOVA

Data Exploration

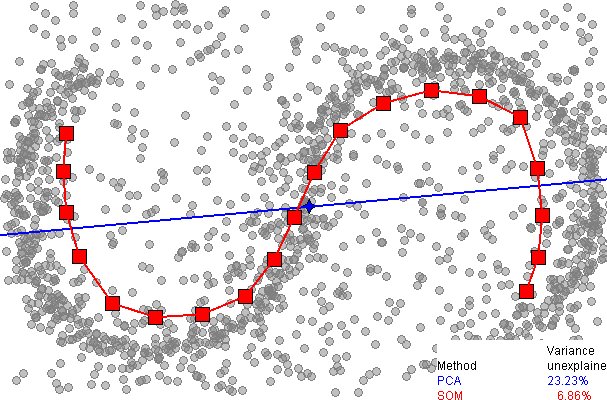
  • Exploring structure of data aka dimensionality reduction
    • Principle component analysis
      • what directions explain the most variance
      • Linear method
    • Kernel tricks + linear methods
    • Manifold learning
      • Assume there is some lower dimensional structure
    • Auto-encoders
      • Neural Networks trained on the identity function

Modelling Themes

Modelling Themes

  • Model? Explain/predict some output by some inputs
  • Minimize error
  • Why build models at all?
    • Incomplete noisy data
    • Discover some latent, hidden process
    • Describe phenomena in more compact form
  • Themes
    • Bias vs Variance
    • Parametric vs non-parametric
    • Frequentist vs Bayesian
 

Bias vs Variance

  • Bias vs Variance: two sources of error 
    • Bias - how much does this model differ from true answer on average
    • Variance - if I build a lot of models using the same process how much will they vary from one another
    • Want low+low, but often they're antagonistic
  • Intuition: predicting election results
    • Only poll people from phone book, that model is biased towards home-phone owning folks -- doesn't matter how many people you poll
    • Only poll 30 people from phone book and you do it multiple times--each time the results might vary. If you increase the number of people, variance will go down

Bias vs Variance

  • Generally the challenge of model fitting: do not want to over-fit or under-fit 
  • In machine learning, we use a methodology of cross-validation
    • train vs test
    • train vs dev vs test
    • ​n-fold validation

Bias vs Variance

  • Variance via model complexity
h_0(x) = b
h0(x)=bh_0(x) = b
h_1(x) = a x + b
h1(x)=ax+bh_1(x) = a x + b
\theta
θ\theta

Parameters = 

 

Parametric vs Non-parametric

  • A few ways to say the same thing?
    • Is there a hidden process that can be described by finite, fixed parameters and can explain the observed data?
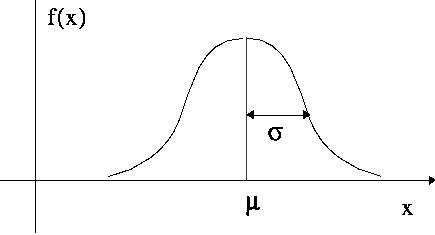
    • Can the data or process be described by a shape that has convenient math properties?
  • Parametric statistical tests assume distributions
  • Non-parametric make fewer assumptions but are often harder to interpret and less powerful

Frequentist vs Bayesian

  • Philosophical difference over interpretation of probability - we'll skip that
  • How it matters to the everyday data scientist?
    • Bayesian treatments
  • ​Quick probability review:
    • % chance of clouds at any moment
    • % chance of rain, given its cloudy
    • Bayes rule:
P( \text{Rain} | \text{Clouds} ) = \frac{P( \text{Clouds} | \text{Rain} ) P( \text{Rain} )}{P( \text{Clouds} )}
P(Rain∣Clouds)=P(Clouds∣Rain)P(Rain)P(Clouds)P( \text{Rain} | \text{Clouds} ) = \frac{P( \text{Clouds} | \text{Rain} ) P( \text{Rain} )}{P( \text{Clouds} )}
P( \text{Clouds} )
P(Clouds)P( \text{Clouds} )
P( \text{Rain} | \text{Clouds} )
P(Rain∣Clouds)P( \text{Rain} | \text{Clouds} )
\text{Posterior} \propto \text{Likelihood} \times \text{Prior}
Posterior∝Likelihood×Prior\text{Posterior} \propto \text{Likelihood} \times \text{Prior}
P( \text{Stroke} | \text{Headache} ) = \frac{P( \text{Headache} | \text{Stroke} ) P( \text{Stroke} )}{P( \text{Headache} )}
P(Stroke∣Headache)=P(Headache∣Stroke)P(Stroke)P(Headache)P( \text{Stroke} | \text{Headache} ) = \frac{P( \text{Headache} | \text{Stroke} ) P( \text{Stroke} )}{P( \text{Headache} )}

Frequentist vs Bayesian

  • Our models have parameters, ​θ, which we set via machine learning based on training data, D


     
  • Allows us to engineer some expert knowledge about the parameters to combat problems with data sparsity, noise, etc.
  • Learning process doesn't find a set of specific parameter values, it finds a distribution over all possible parameter values
    • Google for maximum a posteriori estimation (MAP) vs maximum likelihood estimation (MLE) if you're interested in more 
P( \theta | D ) = \frac{P( D | \theta ) P( \theta )}{P( D )}
P(θ∣D)=P(D∣θ)P(θ)P(D)P( \theta | D ) = \frac{P( D | \theta ) P( \theta )}{P( D )}

Task  & Method Families

Task Families

  • Regression
  • Classification
  • Structured Prediction
  • Clustering
  • Others

Method Families

  • Linear models
  • Probabilistic methods
  • Decision Trees
  • Support Vector Machines
  • Neural Networks
  • Stochastic/Evolutionary methods

Task Families

  • Regression
    • Predict a continuous output value given some input
    • E.g. How many inches of water will fall for cloudy may day?




       
  • Classification
    • Predict a categorical output value given some input
    • E.g. Is this credit card transaction fraudulent?

Task Families

  • Structured Prediction
    • Given this sequence of inputs, predict a sequence of outputs
    • E.g. Assign Parts-of-speech tags to each word



       
  • Clustering
    • Group data points in some way that provides meaning
    • E.g. discovering customers that have similar purchasing habits

Task Families

  • Others
    • Object extraction, identification in images
    • Planning, optimization
    • Time series prediction
 

Model Families

  • Linear Methods
    • no exponents in terms
    • Linear Regression
      • each input variable has a parameter representing the weight of how much that input contributes to the output
      • multiply weight * input and add 'em up to get output
         
    • Regularization - try and encourage the parameter values to stay within a given range
    • Lot's of math tricks that work with this constraint
y(x, \theta) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n
y(x,θ)=θ0+θ1x1+θ2x2+⋯+θnxny(x, \theta) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n

Model Families

  • Probabilistic models
    • Generative vs Discriminative
      • Discriminative: model the desired target variable directly
      • Generative: model a conditional process that generates values then use bayes rule

         
    • Naive Bayes
      • Simplest, generative classifier
    • Logistic Regression
      • Powerful discriminative method of classification
        • Weights the "log odds" of each input
P(C_1|x) = \frac{P(x | C_1) P(C_1)}{P(x | C_1) P(C_1) + P(x | C_2) P(C_2)}
P(C1∣x)=P(x∣C1)P(C1)P(x∣C1)P(C1)+P(x∣C2)P(C2)P(C_1|x) = \frac{P(x | C_1) P(C_1)}{P(x | C_1) P(C_1) + P(x | C_2) P(C_2)}

Model Families

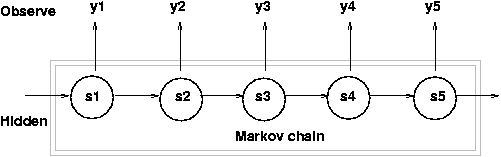
  • Probabilistic Graphical Models
    • E.g. bayes nets, markov random fields, factor graphs
    • Framework for encoding dependence relationships
    • Hidden Markov Model (generative)
    • Conditional Random Fields (discriminative)

Model Families

  • Decision Trees
    • C4.5, C5 popular; especially good at categorical data
    • Typically used for classification, but CART does regression in the leaves
    • Each node in the tree represents the best way to split the data so each sub-tree is more homogenous than the parent
    • At test time, follow tree from root to leaf
  • Random Forests
    • Build lots of trees from resampled training data
    • Average or vote the results
    • Reduces overfitting
    • Example of the technique: bagging

Model Families

  • Support Vector Machines (SVM)
    • Find an optimally separating plane
    • Math tricks (finding support vectors, kernel trick)
    • Excellent discriminative method, commonly limited to binary classification
  • Neural Networks
    • Feed forward, recurrent, hopfield, ARTMap, boltzmann machines, oh my!
    • Deep learning: stacking networks + clever training
  • Stochastic/Evolutionary
    • When all else fails, search forever
    • Particle Swarm (PSO) et al

Learning, Optimization

Learning, Optimization

  • Convex optimization
    • Many methods deliberately assume distributions or constrain the function such that it is convex
    • Calculus tricks (gradients, line search, LBFGS)
  • Stochastic optimization
  • Problems
    • Curse of dimensionality
    • Tractable inference
      • Large graphical models with lots of dependence
  • Incomplete training data
    • Semi-supervised learning
    • Imputation
    • Expectation constraints, posterior regularization

Now the bad news

  • Data Science is hard
    • Which methods, which constraints on methods
  • Mathematical details of model leads to intuition
  • Mind boggling amount of information, growing quickly
  • Multi-disciplinary history -> overlapping concepts, words, notation -> confusion
  • Tools are maturing quickly but there is still large gap between day to day exploration and modelling and production end-user value
  • Hard to hire
    • Unicorns are hard to find
    • Easy for ignorant charlatans to convince otherwise unsuspecting non-technical people that they know how to data science

The End

A brief, whirlwind tour of data science

By Steve Ash

Made with Slides.com

A brief, whirlwind tour of data science

  • 3,411