Why Majoranas are cool
Zhi Han
Disclaimer
- I am not expert in the subject of condensed matter.
- Status of Majorana particle is still unconfirmed.
- All the material can be found on https://topocondmat.org/index.html
How/why might Majoranas play a role in fault tolerance?
How/why might Majoranas be used for quantum computing?
1: Symmetry and Topology
Topology
-
Topology looks at invariant properties of objects under continuous transformations.

Topology
-
We say two Hamiltonians are topologically equivalent if they can be deformed into each other without crossing E = 0.

Topological Invariant
-
Count the number of energy levels below E = 0.
-
This number cannot change under continuous transformations.
-
Call this idea a topological invariant.

Unitary Symmetry
Transform \(H\) into another of the same type.
\(H\) is block diagonal. Any guesses?
Conservation law:
\[UH = HU, \quad U = \hat \sigma_z \otimes 1\]

\[UH = HU, \quad U = \hat \sigma_z \otimes 1\]
Sublattice Symmetry
Transform \(H\) into another of the same type.
\(H\) is off diagonal. Any guesses?
Conservation law:
\[\sigma_z H = -H \sigma_z\]

\[\sigma_z H = -H \sigma_z\]
State \(|\psi_A \psi_B\rangle\) has energy \(E\)
implies \(|\psi_A, -\psi_B \rangle\) has energy \(- E\)
\[\sigma_z H = -H \sigma_z\]
Superconductors
BCS theory:
-
Electrons in superconductors can be created/destroyed in pairs. (Cooper pairs)
-
Particle number not conserved.
Superconductors
\( c^\dagger_i \) = create particle at site \(i\)
\( c_i \) = destroy particle at site \(i\)
particle moving from \(m\) to \(n\)
creating and destroying pairs at \(m, n\)
Superconductors
Rewrite as quadratic form
Vector of creation and annhilation operators
Bogoliubov-de Gennes
Hamiltonian.
Topological properties?
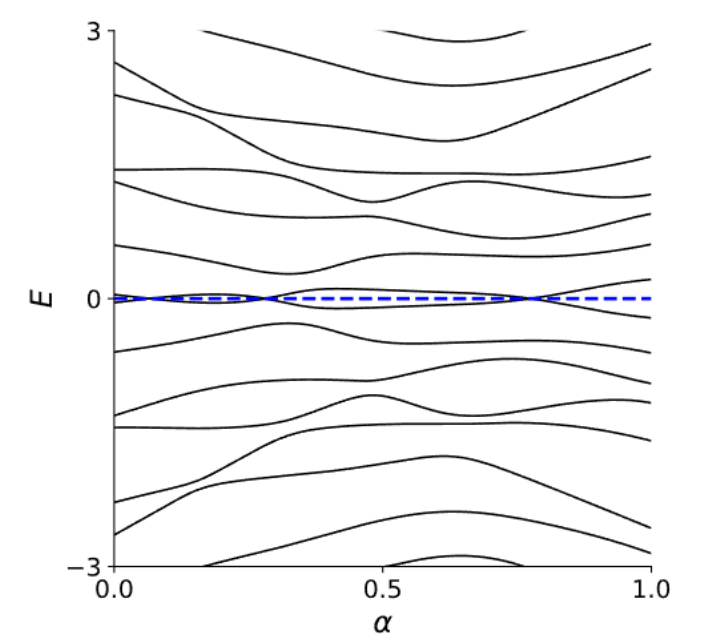
BdG Hamiltonian. Note we are allowed to cross H = 0.
Let's think about this
-
A superconductor has \(n\) sites where an electron \(c^\dagger_i\) can be created.
-
By converting to a \(H_{BdG}\) we artificially introduced a vector C. This doubled the degrees of freedom from \(n\) to \(2n\).
-
This means energy \(E\) and \(-E\) in \(H_{BdG}\) corresponds to the same state. This is different than the off-diagonal case where the two states are independent.
Let's think about this
-
To imagine \(E\) and \(-E\) in \(H_{BdG}\) as two independent states, we might imagine a new operator.
-
This is called Bogoliubov quasiparticle and is a superposition of particle and hole.
Let's think about this
- When a energy levels crosses \(E = 0\), the even/oddness of \(H_{BdG}\) changes.
- This is the topological invariant for a superconductor called the Plaffian, or fermion parity.
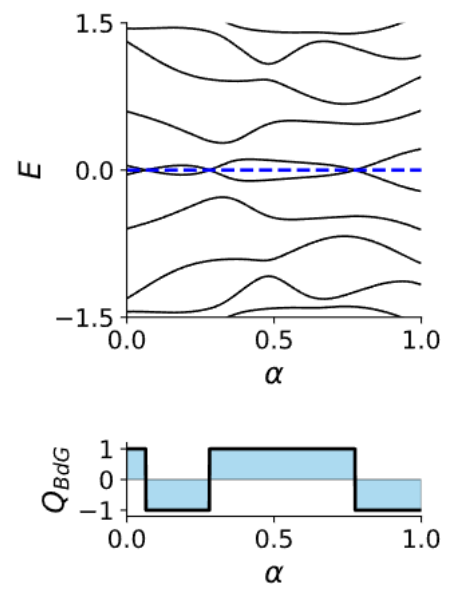

Summary
-
Symmetries give rise to topological properties.
-
(BCS) superconductors have a particle hole symmetry.
-
i.e. particles and "antiparticles/holes" feel the same interactions.
-
-
The BdG spectrum is symmetric from \(E\) to \(-E\) and corresponds to the same state.
-
However, we can imagine that they are two different quasi states.
-
The topological invariant is the fermion parity, or even/oddness detector called the Plaffian.
Symmetry
Topological Invariants
Particle Hole
Sublattice
Plaffian (Fermion parity)
# of Eigenstates
below E = 0
Topological Properties
Symmetric Eigenspectrum
2: Majoranas are protected by symmetry
You might guess…
-
“I know how where this talk is going!” you say.
-
“You’re just going to come up with two systems with different Plaffians. One is even and the other is odd. If there is something interesting about one of the two systems, we can just keep staying in that system, because to change the system, you must change the topological invariant!
-
That something, is the Majorana fermion and is exactly the fault tolerant behaviour we care about.
Creation and destruction
In quantum mechanics and quantum field theory, the creation and destruction operators for fermions (in momentum space) are:
This can be neatly summed up by the following rules:
Creation and destruction
For a single fermion, we have:
But for multiple particles, we have: (using the anticommutator:)
A unitary transformation
When you have a pair of creation and destruction operators, you can write down the following unitary transformation:
The pair \(\gamma_1\) and \(\gamma_2\) are called Majorana operators. Notice that \(\gamma\) = \(\gamma^\dagger\).
Because \(c^\dagger, c\) must be fermion operators, this gives a constraint on the Majorana operators:
Majoranas algebra
A single fermion as two Majoranas \(\gamma_1, \gamma_2 \) has the anti-commutation relation:
Multiple Majoranas: (\(\gamma_i = \gamma^\dagger_i\))
Fermions algebra
A single fermion has the anti-commutation relation:
Multiple fermions:
Majorana Particles
Does this mean we just found a particle that is it's own antiparticle? This is the theoretical prediction made by Ettore Majorana in 1937.

How to generate Majoranas
One proposed model containing Majoranas is the Kitaev chain. The Kitaev chain is just \(n\) electrons in a row:
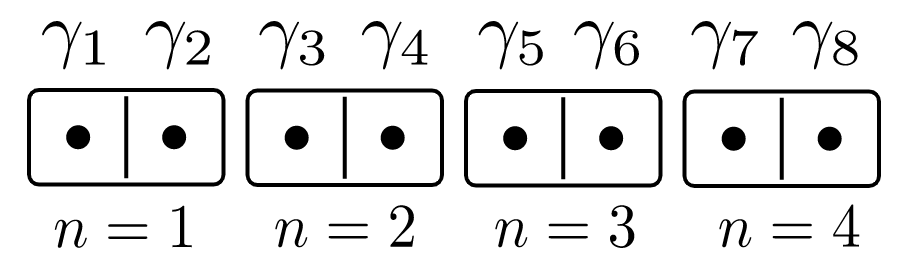
Let's saw an electron in half!
The Trivial Phase
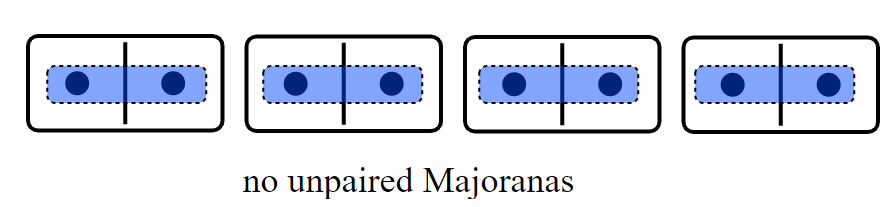
No unpaired Majoranas, and each majorana having energy \(\mu/2\):
The Topological Phase
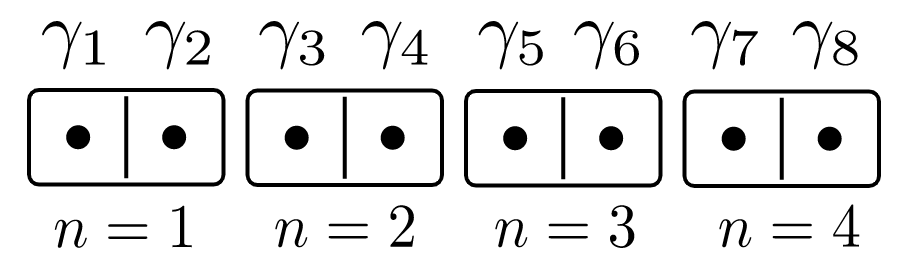
Or like this, each Majorana having an energy \(t\):
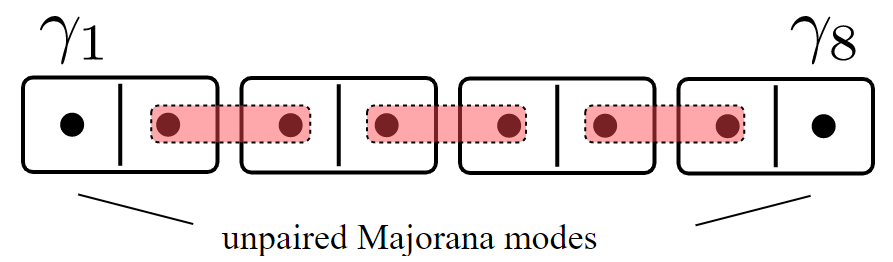
The Kitaev Chain
We can put it into one Hamiltonian, and converting back from Majoranas to electrons we obtain the model of the Kitaev chain:
We switch phases at \( \mu = 2t \).
Rewrite this in terms of fermion operators, and what do we get?
The Kitaev Chain
We can put it into one Hamiltonian, and converting back from Majoranas to electrons we obtain the model of the Kitaev chain:
-
\(\mu\) is the chemical potential
-
\(t\) is the kinetic energy
-
\(\Delta\) is the superconducting band gap
We switch phases at \( \mu = 2t \).
-
\(\mu\) is the chemical potential
-
\(t\) is the kinetic energy
-
\(\Delta\) is the superconducting band gap
We switch phases at \( \mu = 2t \).
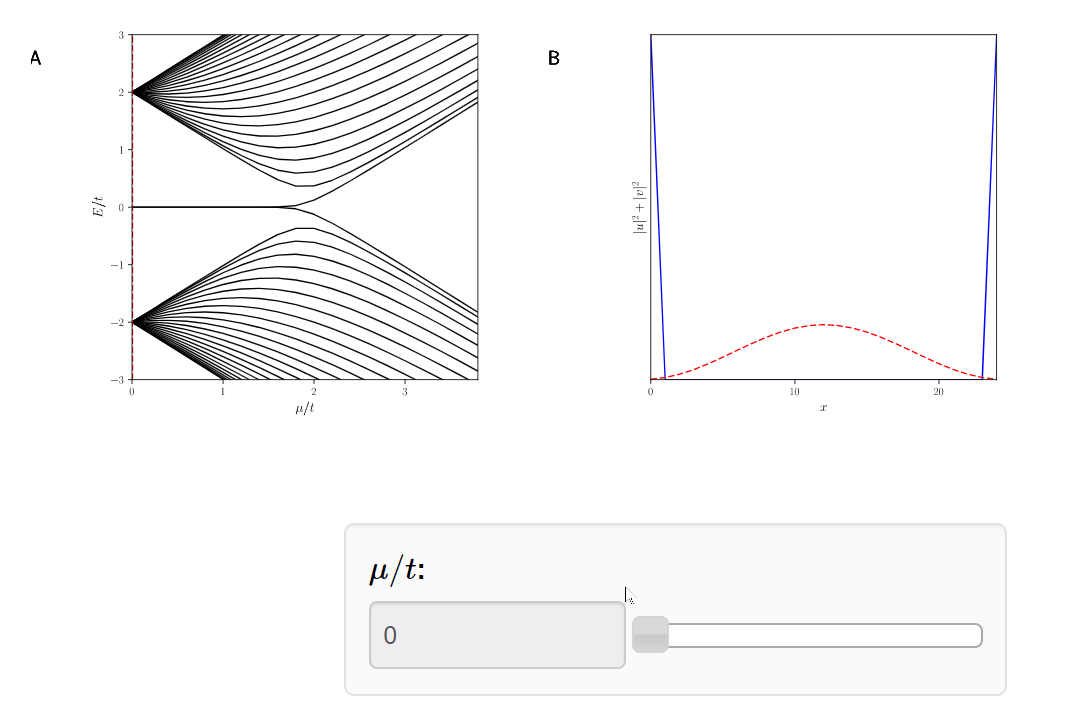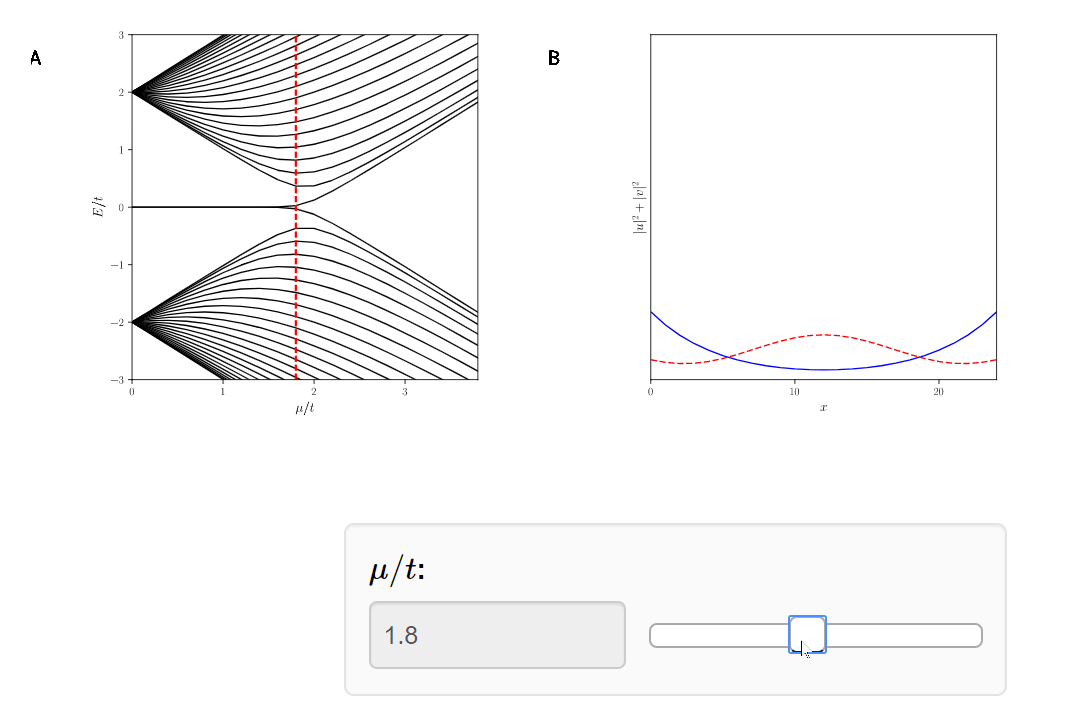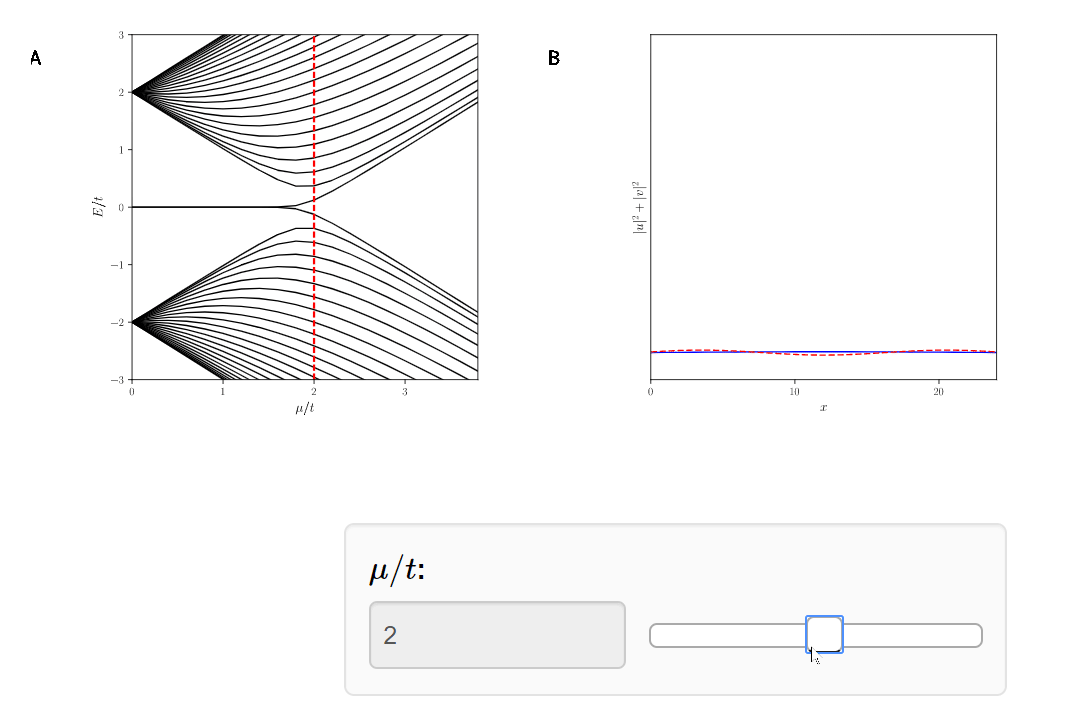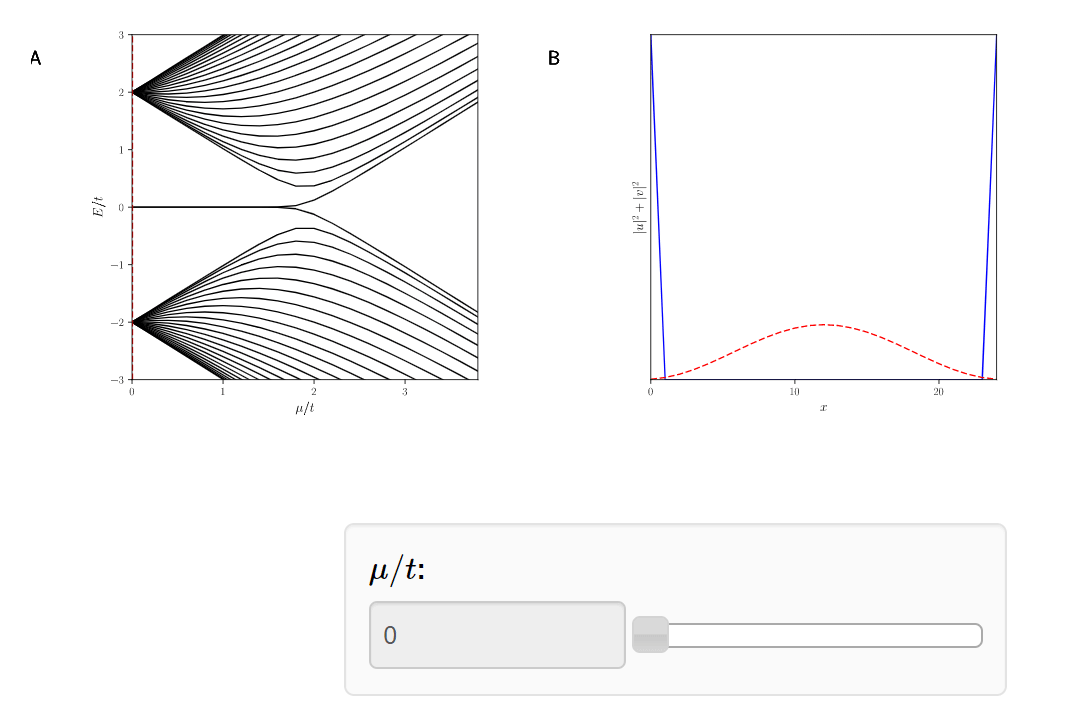
Topological \( |\mu|<2t\)
Trivial \( |\mu|\geq2t\)
- This is called a topological quantum phase transition.
- The Plaffian, the topological invariant in Particle Hole symmetry, has for:
- Q = -1 (topological)
- Q = +1 (trivial)
- Thus, it is impossible to go from one system to the other without bringing together the Majoranas.
- https://topocondmat.org/w1_topointro/1D.html
Topological Phase Transition
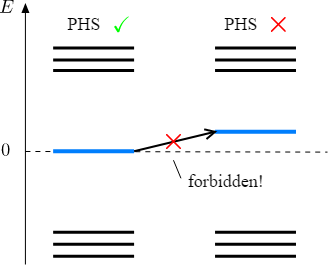
Quantum Phase Transition!
Why do we care?
The Majoranas are a topological property of the system. Therefore if we slice off the Kitaev Chain, a new Majorana will appear.


Again, this is because the topological phase has Q = -1.
Summary
-
The Kitaev Chain, a toy model of a superconducting wire, hosts two topological quantum phases.
-
The topological phase, corresponding to Q = -1.
-
The trivial phase, corresponding to Q = +1.
-
-
The Majoranas live on the boundary of a superconducting wire and are protected by topology and symmetry.
-
The boundary being a topological property.
-
Particle hole symmetry forbidding energy transitions.
-
3: Topological Quantum
Computation
Topological QC

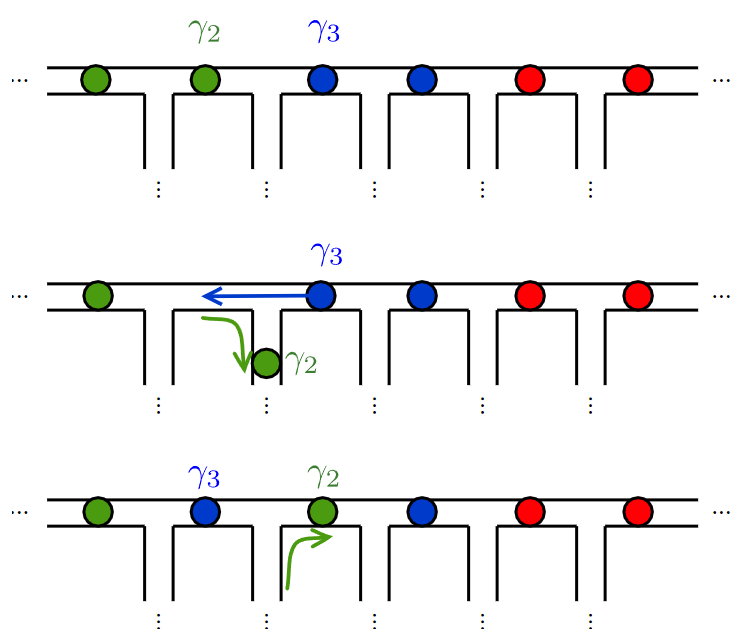

- Closed trajectory and is under adiabatic limit.
- Can only depend on pairs of Majoranas \(\gamma_n \gamma_m\).
- Exponential of \(i\) times Hermitian is Unitary. \(-i \gamma_n \gamma_m\), the exchange operator is Hermitian.
- Fermion parity is conserved under exchange.

Heisenberg equation
Closed trajectory. Thus, H(T) = H(0)
Logical Qubits
- Logical qubit is given by \( |00\rangle, |11\rangle\), since fermion parity is odd if we just use \(|0\rangle, |1\rangle \).

[3]
Limitations
- Braiding is not universal. Only can get Pauli gates X, Y, Z. [2]
- No entanglement gates.
- For universality, need to either consider Majorana/Qubit hybrid systems or temporarily get out of the topological phase. (i.e, consider non protected operations)
- Existence of Majorana fermions is still debated.
- Great quantum memory to store your quantum Bitcoin.
- Protected vs Bit-flip and phase shift errors. [2]
- Quasiparticle poisoning. [3]
You and your buddy were made in a pair,
Then wandered around, braiding here, braiding there.
You'll fuse back together when braiding is through
Well bid you adieu as you vanish from view.
Alexei exhibits a knack for persuading
That someday we'll crunch quantum data by braiding, With quantum states hidden where no one can see, Protected from damage through topology.
Anyon, anyon, where do you roam?
Braid for a while ... before you go home.
References
[1]Topology in Condensed Matter Course (Main reference)
[2]M. Leijnse and K. Flensberg, Introduction to Topological Superconductivity and Majorana Fermions, Semicond. Sci. Technol. 27, 124003 (2012).
[3]C. W. J. Beenakker, Search for Majorana Fermions in Superconductors, Annu. Rev. Condens. Matter Phys. 4, 113 (2013).
[4]B. Field and T. Simula, Introduction to Topological Quantum Computation with Non-Abelian Anyons, Quantum Sci. Technol. 3, 045004 (2018).
Majorana Talk
By Zhi Han
Majorana Talk
- 832



