1.3 Six Elements of ML
A defining framework for understanding concepts in the course

Recap: Machine Learning
What we saw in the previous chapter?
(c) One Fourth Labs


A jargon cloud
How do you make sense of all the jargon?
(c) One Fourth Labs


From jargons to jars
What are the six jars of Machine Lerarning
(c) One Fourth Labs


Data data everywhere
What is the fuel of Machine Learning?
(c) One Fourth Labs















Data data everywhere
How do you feed data to machines ?
(c) One Fourth Labs

We encode all data into numbers - typically high dimension
For instance, in this course you will learn to embed image and text data as large vectors
Data entries are related - eg. given a MRI scan whether there is a tumour or not
Include a table that shows two/three MRI scans in first col, shows large vectors in second column, 1/0 for last column of whether there is tumour or not
Include a table that shows two/three reviews in first col, shows large vectors in second column, 1/0 for last column for whether review is positive or negative
Title the columns as x and y




All data encoded as numbers
Typically high dimensional
| scans | ||
|---|---|---|
| 2.3 | 5.9 | ... | 11.0 | -0.3 | 8.9 | 0 |
|---|
| -8.5 | -1.7 | ... | -1.3 | 9.0 | 7.2 | 1 |
|---|
| -0.4 | 6.7 | ... | -2.4 | 4.7 | -7.3 | 0 |
|---|
| 1.6 | -0.4 | ... | -4.6 | 6.4 | 1.9 | 1 |
|---|



| 3.9 | -4.1 | ... | 6.7 | -3.1 | 2.1 | 1 |
|---|
| 5.1 | 3.7 | ... | 1.8 | -4.2 | 9.3 | 1 |
|---|

Data data everywhere
How do you feed data to machines ?
(c) One Fourth Labs

We encode all data into numbers - typically high dimension
For instance, in this course you will learn to embed image and text data as large vectors
Data entries are related - eg. given a MRI scan whether there is a tumour or not
Include a table that shows two/three MRI scans in first col, shows large vectors in second column, 1/0 for last column of whether there is tumour or not
Include a table that shows two/three reviews in first col, shows large vectors in second column, 1/0 for last column for whether review is positive or negative
Title the columns as x and y
All data encoded as numbers
Typically high dimensional
| Document | ||
|---|---|---|
| 1.9 | 3.2 | ... | -9.8 | -6.7 | 1.2 |
|---|
| 1.3 | 3.6 | ... | -5.4 | 9.1 | 2.3 |
|---|
| 0.4 | 7.6 | ... | -0.1 | -1.4 | 8.7 |
|---|
| 1.5 | -0.8 | ... | 7.8 | 8.4 | 0.3 |
|---|

Don't buy this MI 6 Pro, Speaker volume is very bad
Delivered as shown. Good price and fits perfect
What a phone.. A handy epic phone. MI at its best ...
Its look stunning in pictures , but not in real.
negative
negative
positive
positive
Amazing camera and battery. Good deal!
| 2.5 | -5.7 | ... | 0.9 | 5.3 | -8.1 |
|---|
positive

Data data everywhere
How do you feed data to machines ?
(c) One Fourth Labs





| 1.3 | -4.3 | 2.1 | -6.7 | ... | 1.5 | 8.9 | 10.1 | -4.5 |
| 2.6 | 7.9 | -0.3 | 8.1 | ... | -4.2 | 0.3 | 1.2 | 9.4 |
| -5.2 | -3.2 | 4.2 | 0.3 | ... | 3.5 | 8.3 | -1.4 | -8.7 |
| 8.5 | 2.1 | -6.3 | 5.3 | ... | 7.2 | -1.3 | -4.5 | 11.8 |
| 2.3 | -5.6 | -1.2 | 7.8 | ... | 9.9 | 10.1 | -1.1 | 3.5 |
All data encoded as numbers
Typically high dimensional
In this course


text
image

Data curation
Where do I get the data from?
(c) One Fourth Labs






I am lucky
I am rich
I am smart

+ मुंबई

= मुंबई
In this course

Data data everywhere
What is the fuel of Machine Learning?
(c) One Fourth Labs

Data

Tasks
What do you do with this data?
(c) One Fourth Labs

Input
Output

















Hello John,
Hello John,
From product description to structured specifications
From specifications + revies to writing FAQs
From specifications + reviews + FAQs to Question Answering
From specifications + reviews + personal data to recommendations





+


+

+


Hello John,

(c) One Fourth Labs
Tasks
What do you do with this data?
(c) One Fourth Labs






From images identify people

Shahrukh Khan
Aamir Khan
From images identify activities

Eating
From images identify places

Gym

From posts recommend posts

Output
Input
Tasks
What do you do with this data?
(c) One Fourth Labs

Supervised
Classification






| 3.2 | 5.9 | ... | 11.0 | 8.9 | 1 |
|---|
| -8.5 | -1.7 | ... | 9.0 | 7.2 | 1 |
|---|
| -0.4 | 6.7 | ... | 4.7 | -7.2 | 0 |
|---|
| 2.7 | 3.1 | ... | -2.1 | 9.7 | 0 |
|---|
| 3.9 | 7.8 | ... | -5.1 | 3.7 | 0 |
|---|
| 7.1 | 0.9 | ... | 1.5 | -4.2 | 1 |
|---|







Tasks
What do you do with this data?
(c) One Fourth Labs

Supervised
Regression



| -8.5 | -1.7 | ... | 9.0 | 7.2 | 2.3 | 1.2 | 9.2 | 10.1 |
|---|
| 0.9 | -2.1 | ... | -8.1 | 1.9 | 4.3 | 4.2 | 7.1 | 5.1 |
|---|
| 2.9 | -4.5 | ... | -3.7 | 8.9 | 2.3 | 7.2 | 6.9 | 7.3 |
|---|

Tasks
What do you do with this data?
(c) One Fourth Labs

Clustering
Unupervised



| 3.2 | 5.9 | ... | 11.0 | 8.9 |
|---|
| -8.5 | -1.7 | ... | 9.0 | 7.2 |
|---|
| -0.4 | 6.7 | ... | 4.7 | -4.1 |
|---|
| 2.7 | 3.1 | ... | -2.1 | 9.7 |
|---|
| 3.9 | 7.8 | ... | -5.1 | 3.7 |
|---|
| 7.1 | 0.9 | ... | 1.5 | -4.2 | 1 |
|---|















Tasks
What do you do with this data?
(c) One Fourth Labs

Generation
Unupervised

| 3.2 | 5.9 | ... | 11.0 | 8.9 |
|---|
| -8.5 | -1.7 | ... | 9.0 | 7.2 |
|---|
| -0.4 | 6.7 | ... | 4.7 | -4.1 |
|---|
| 2.7 | 3.1 | ... | -2.1 | 9.7 |
|---|
| 3.9 | 7.8 | ... | -5.1 | 3.7 |
|---|
| 7.1 | 0.9 | ... | 1.5 | -4.2 | 1 |
|---|






Tasks
What do you do with this data?
Generation
Unupervised
| Tweets | |
|---|---|
| 2.3 | 5.9 | ... | 11.0 | -0.3 | 8.9 |
|---|
| -8.5 | -1.7 | ... | -1.3 | 9.0 | 7.2 |
|---|
| -0.4 | 6.7 | ... | -2.4 | 4.7 | -6.2 |
|---|
| 1.6 | -0.4 | ... | -4.6 | 6.4 | 1.9 |
|---|





(c) One Fourth Labs

Tasks
What do you do with this data?
(c) One Fourth Labs

\( `` \)
Supervised Learning has created 99% of economic value in AI
In this course
Classification
Regression








Tasks
What do you do with this data?
(c) One Fourth Labs

Data


Task
What is the mathematical formulation of a task?
(c) One Fourth Labs


\( x \)
\( y \)
bat
car
dog
cat
Models
\( \left[\begin{array}{lcr} 2.1, 1.2, \dots, 5.6, 7.2 \end{array} \right]\)
\( \left[\begin{array}{lcr} 0, 0, 1,0, 0 \end{array} \right]\)
\( y = f(x) \) [true relation, unknown]
\( \hat{y} = \hat{f}(x) \) [our approximation]


ship

\( \left[\begin{array}{lcr} 0, 1, 0, 0, 0 \end{array} \right]\)
\( \left[\begin{array}{lcr} 0, 0, 0, 0, 1 \end{array} \right]\)
\( \left[\begin{array}{lcr} 1, 0, 0, 0, 0 \end{array} \right]\)
\( \left[\begin{array}{lcr} 0, 0, 1, 0, 0 \end{array} \right]\)
\( \left[\begin{array}{lcr} 0.1, 3.1, \dots, 1.7, 3.4\end{array} \right]\)
\( \left[\begin{array}{lcr} 0.5, 9.1,\dots, 5.1, 0.8 \end{array} \right]\)
\( \left[\begin{array}{lcr} 1.2, 4.1, \dots, 6.3, 7.4 \end{array} \right]\)
\( \left[\begin{array}{lcr} 3.2, 2.1, \dots, 3.1, 0.9 \end{array} \right]\)

Models
What are the choices for \( \hat{f} \) ?
(c) One Fourth Labs

\( \hat{y} = mx + c \)
\(\hat{ y} = ax^2 + bx + c \)
\( y = \sigma(wx + b) \)
\( y = Deep\_NN(x) \)
\( \hat{y} = \hat{f}(x) \) [our approximation]
\( \left [\begin{array}{lcr} 0.5\\ 0.2\\ 0.6\\ \dots\\0.3\ \end{array} \right]\)
\( \left [\begin{array}{lcr} 14.8\\ 13.3\\ 11.6\\ \dots\\6.16 \end{array} \right]\)
\( x \)
\( y \)
\(\hat{ y} = ax^3 + bx^2 + cx + d \)
\(\hat{ y} = ax^4 + bx^3 + cx + d \)
Data
In this course
\( y = Deep\_CNN(x) \) ...
\( y = RNN(x) \) ...
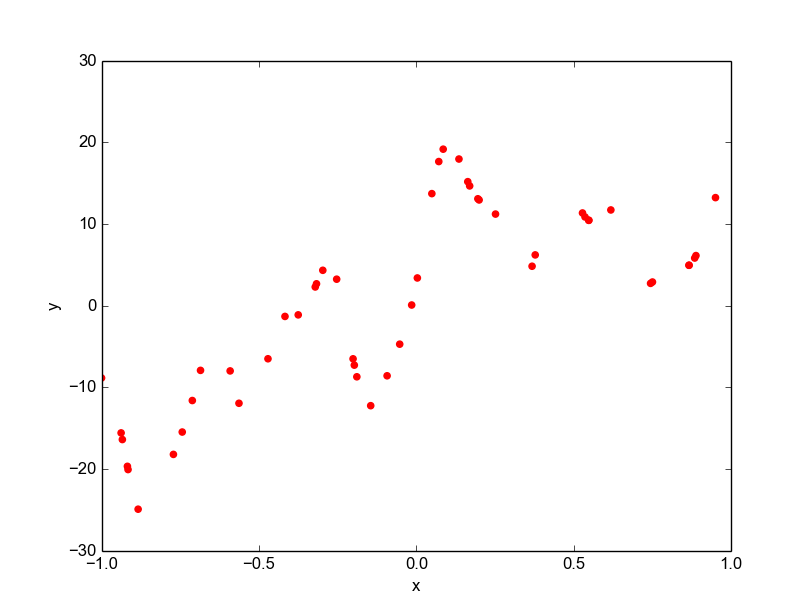

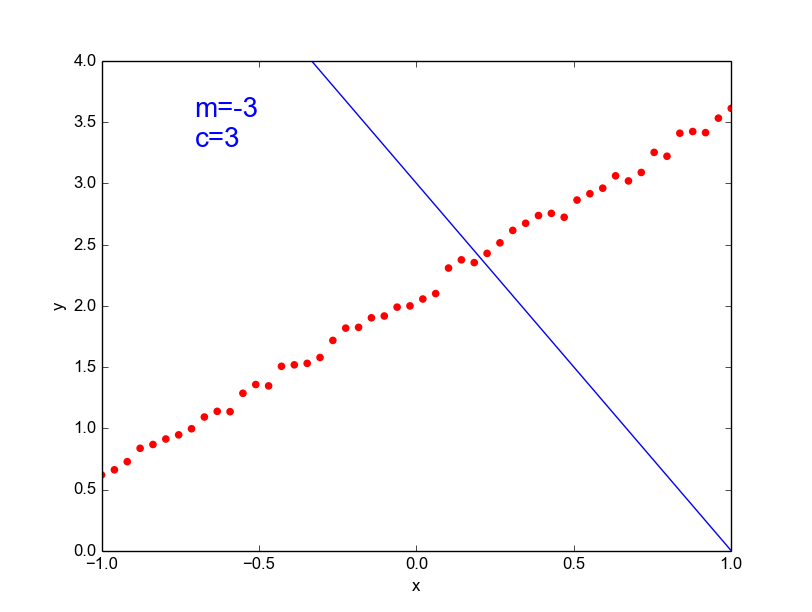
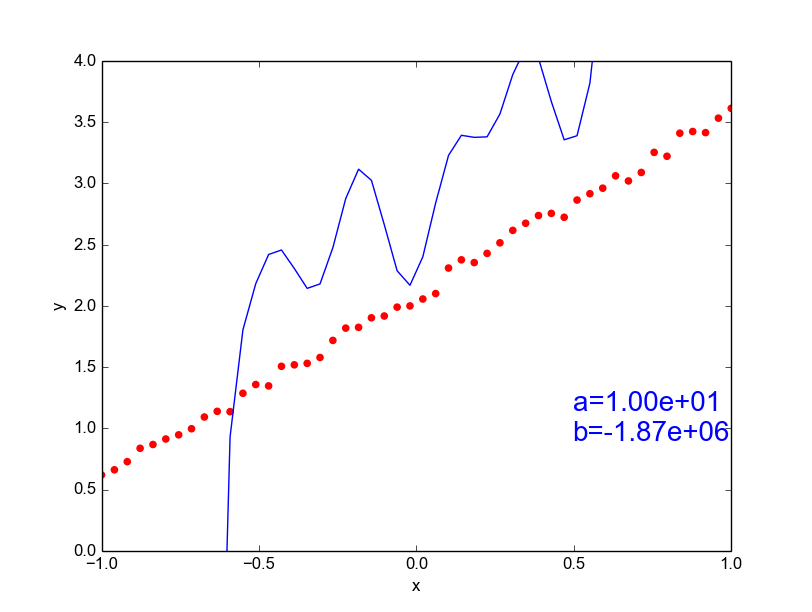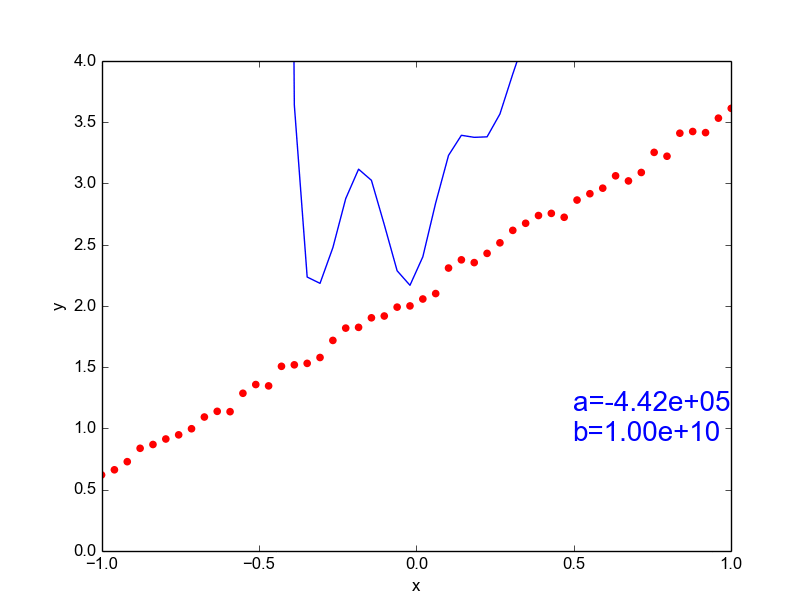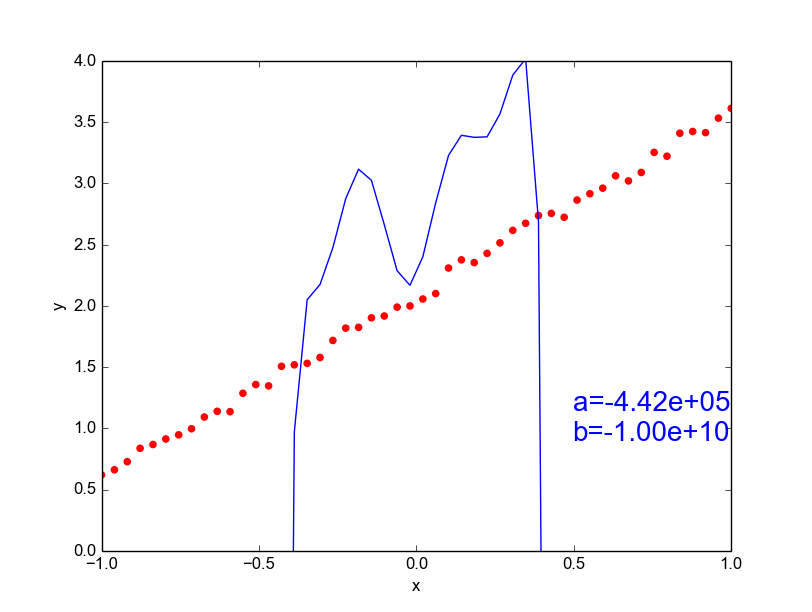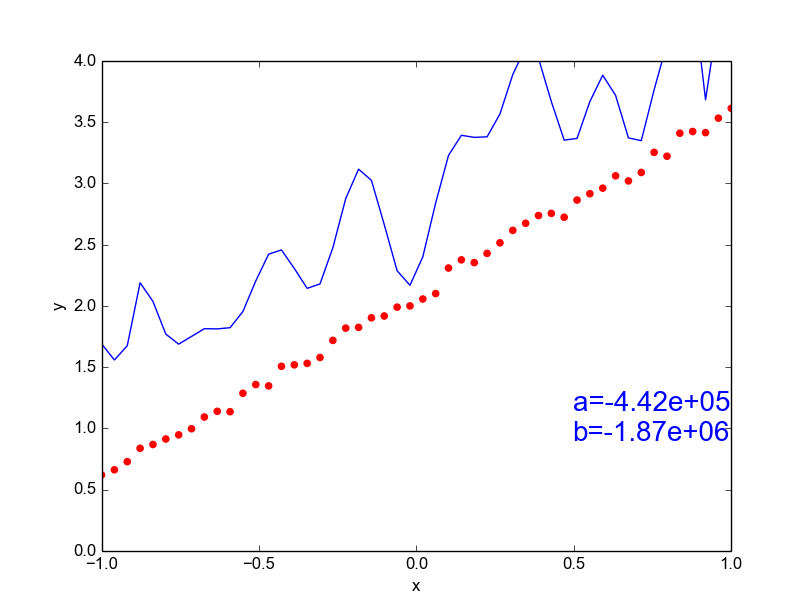
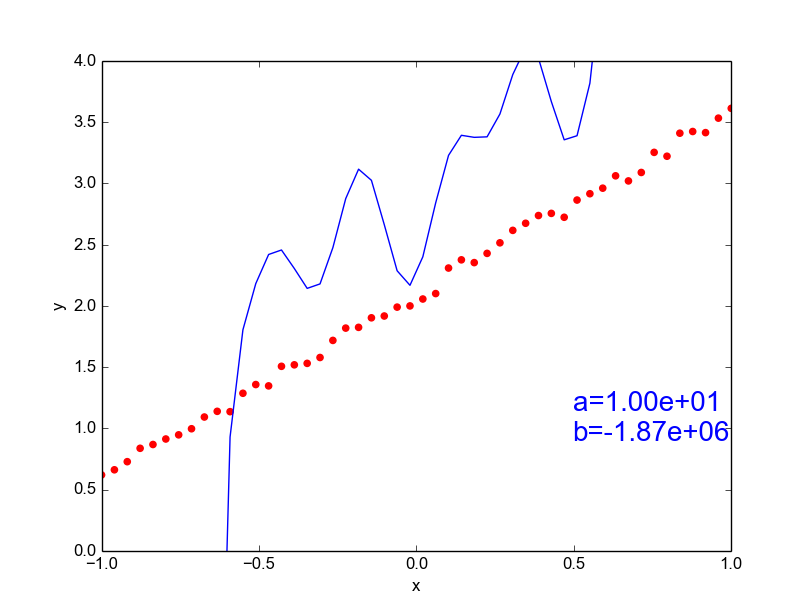
Data is drawn from the following function
\(\hat{ y} = ax^{25} + bx^{24} + \dots + cx + d \)
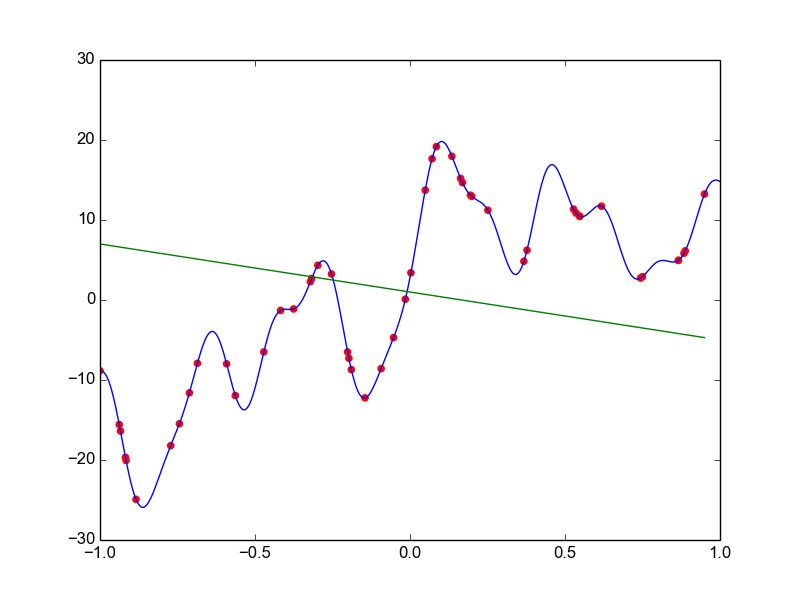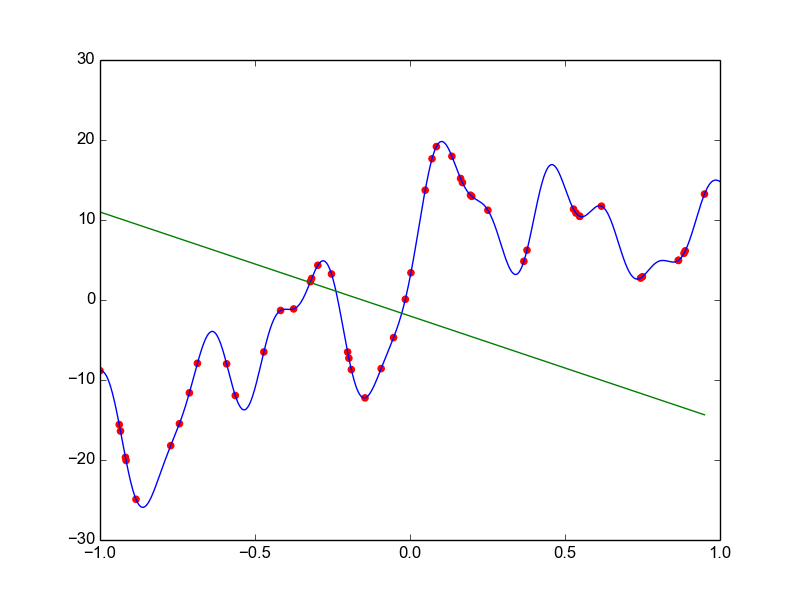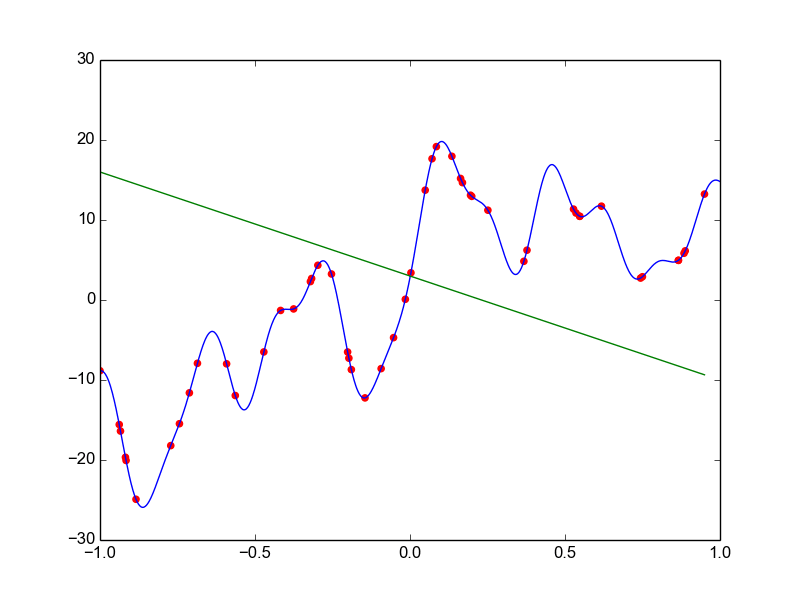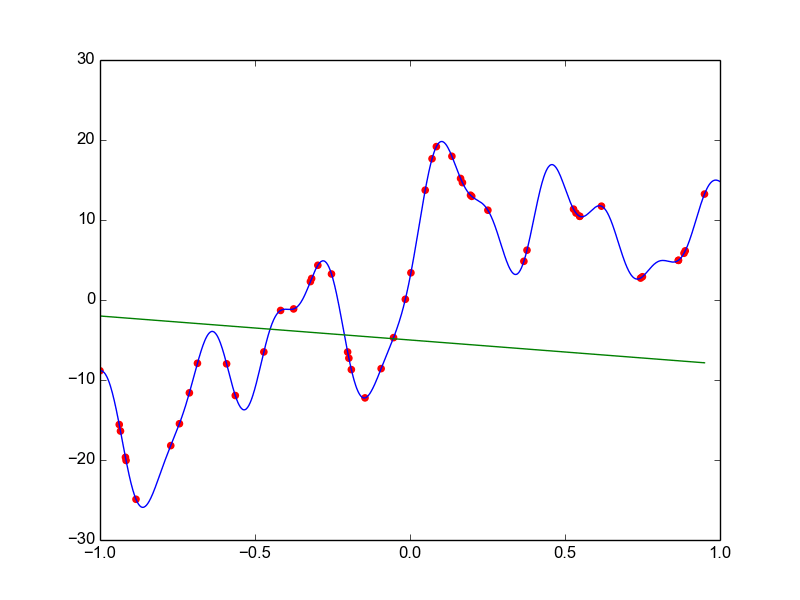
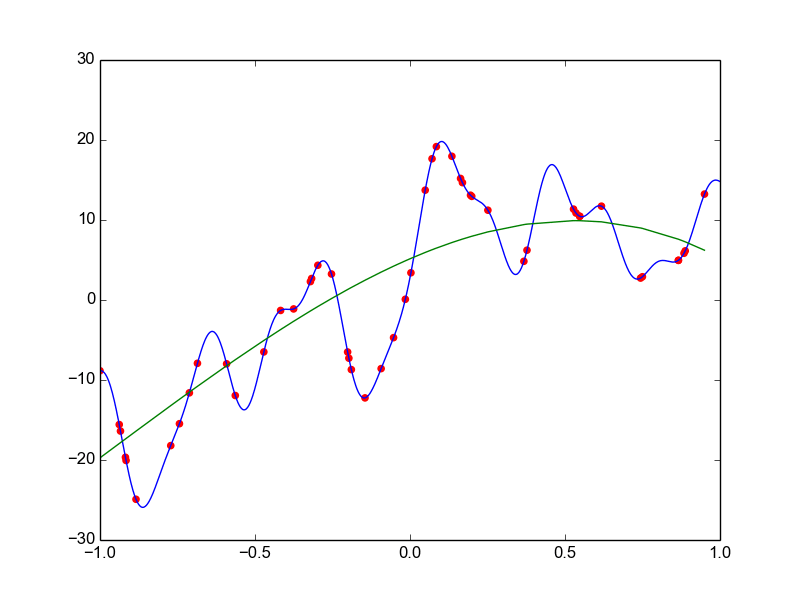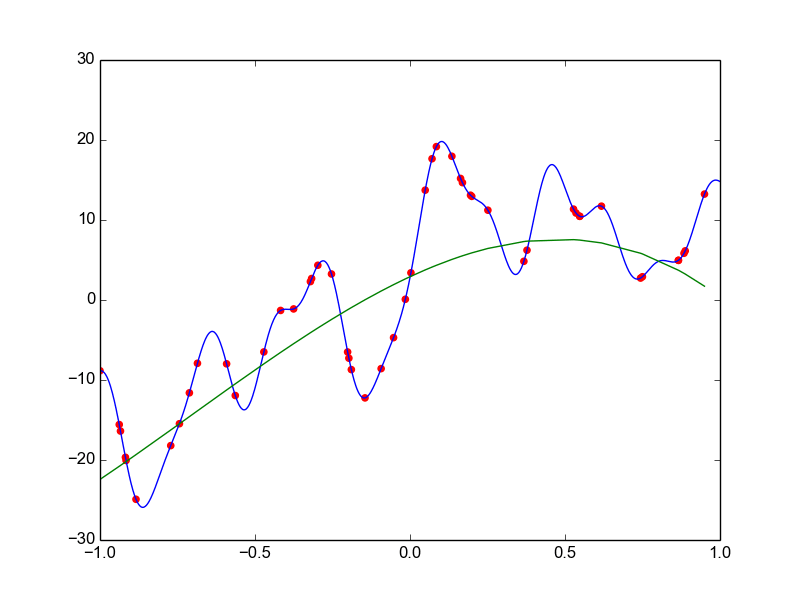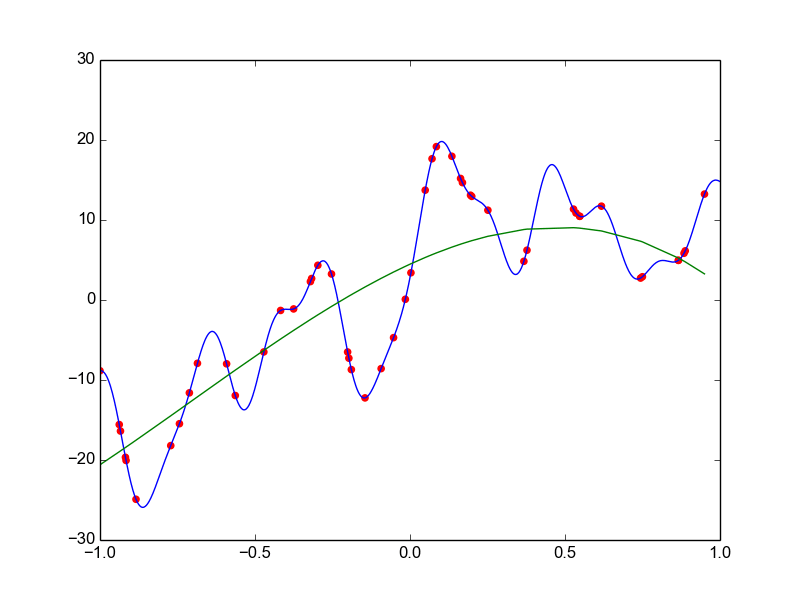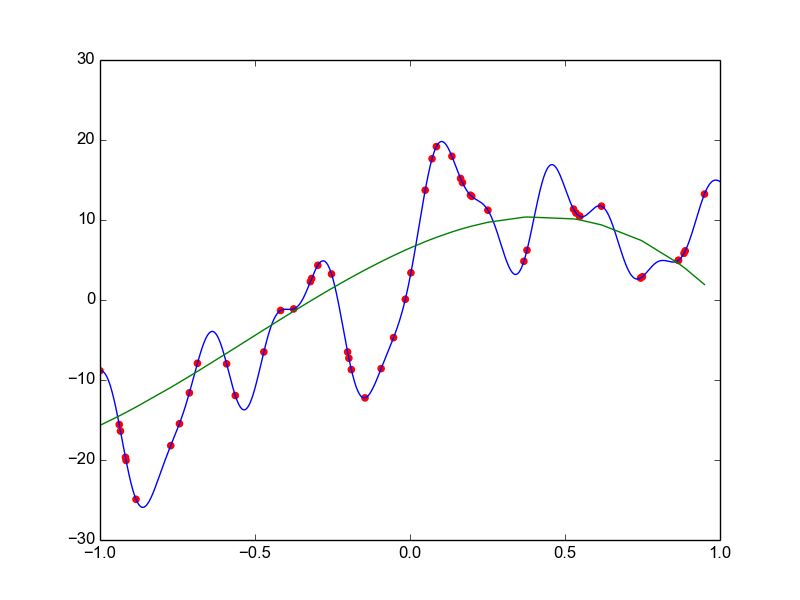
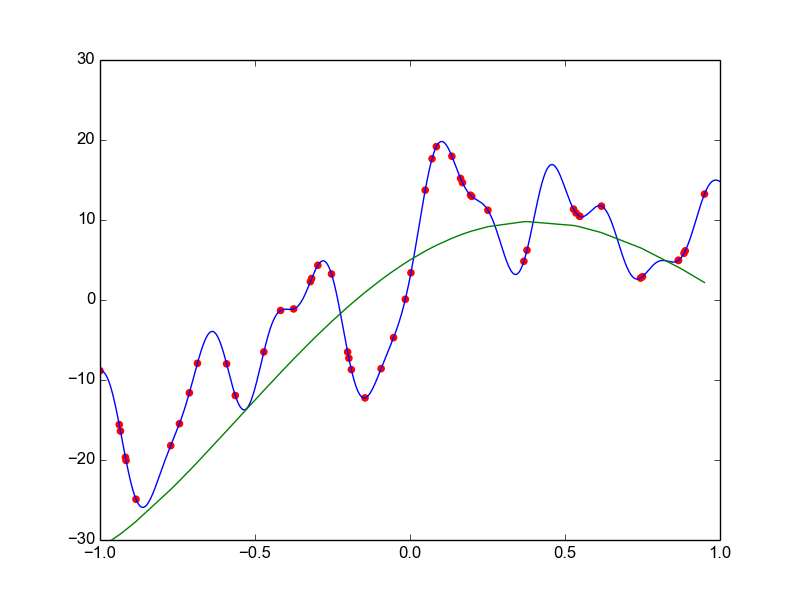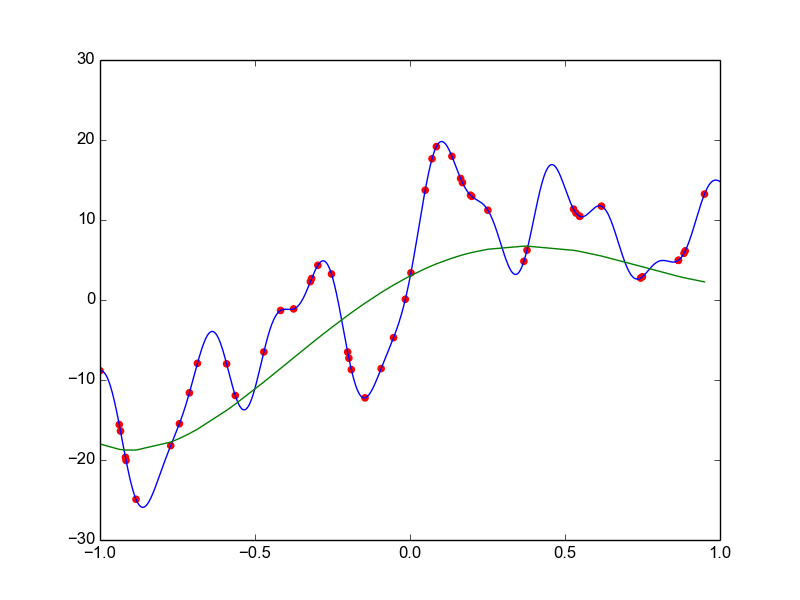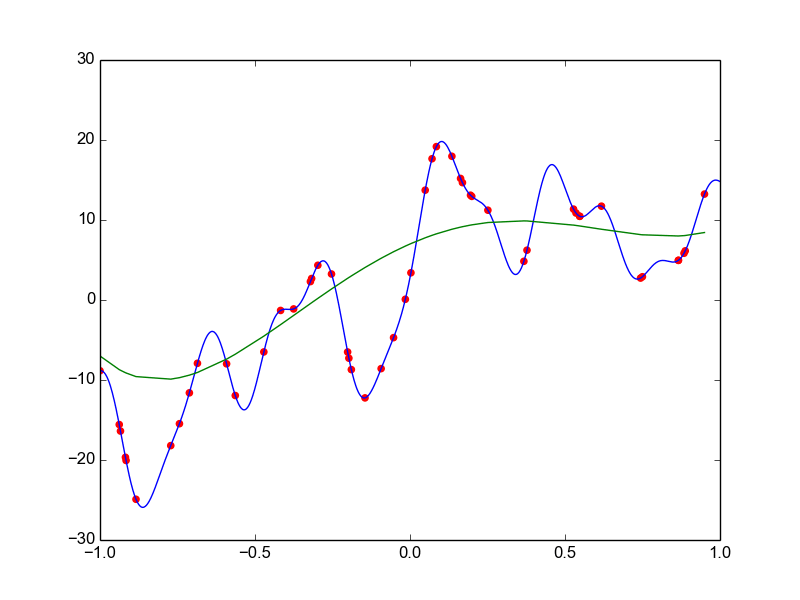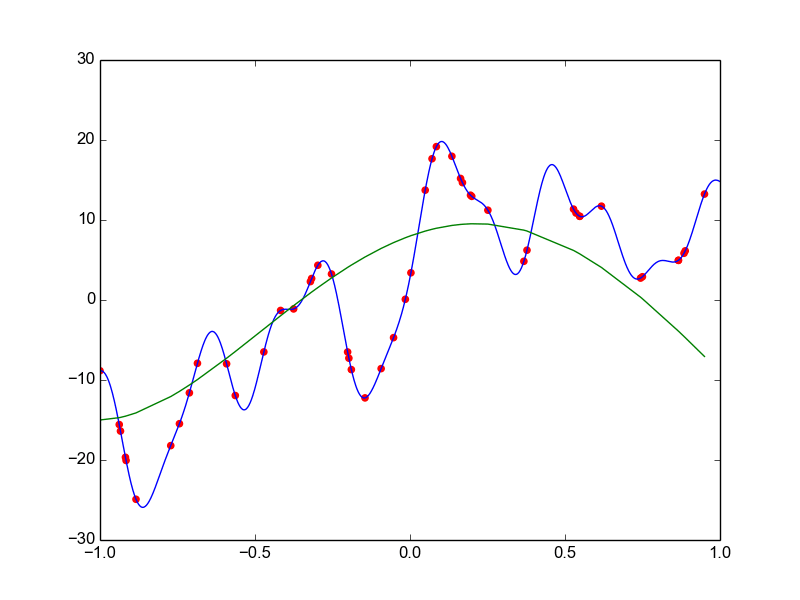
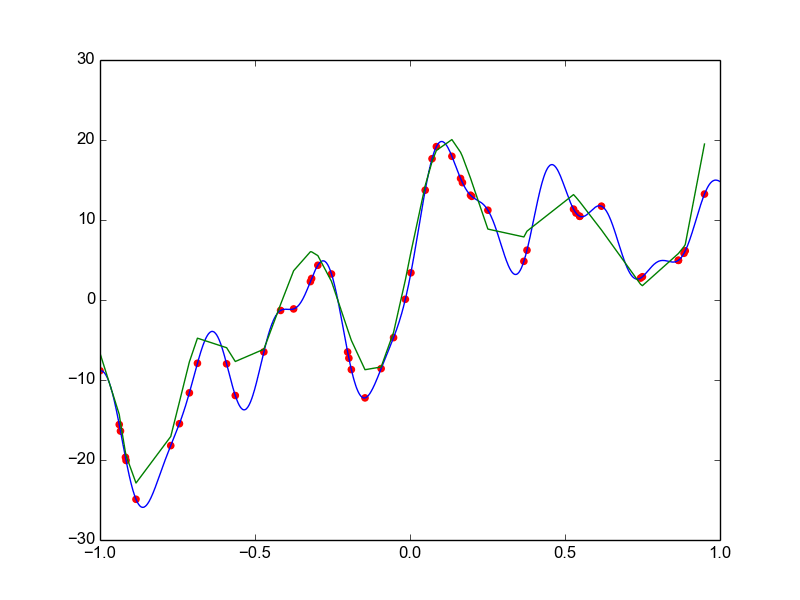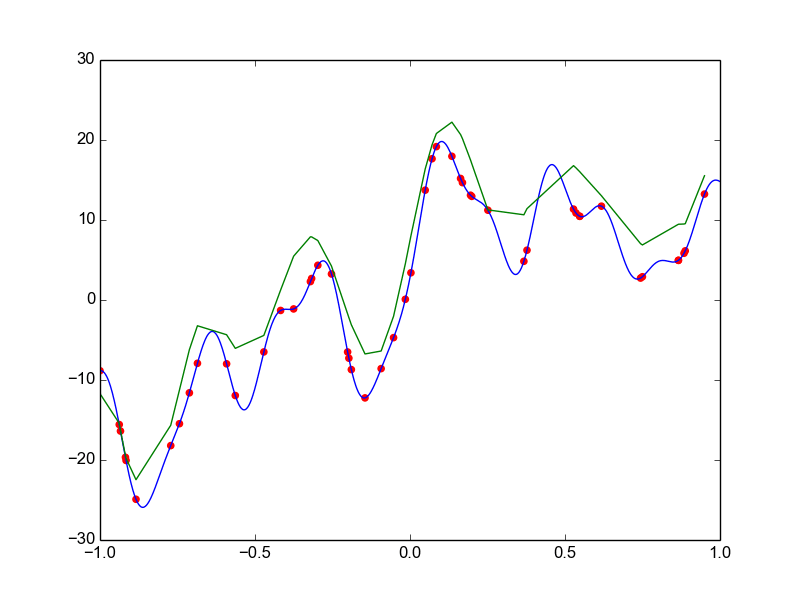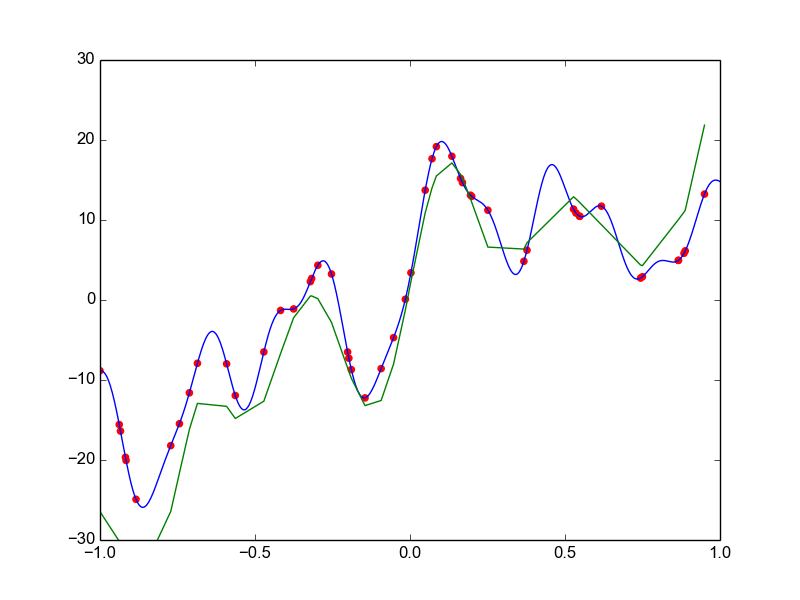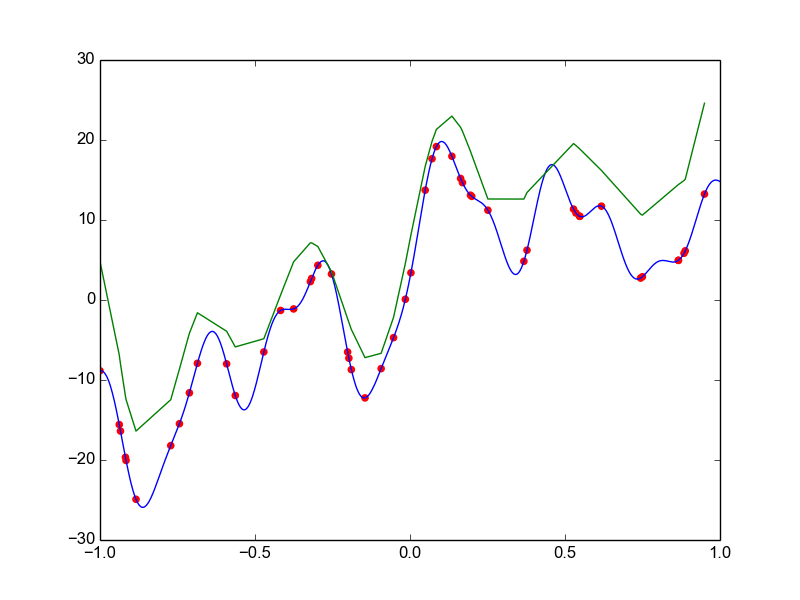
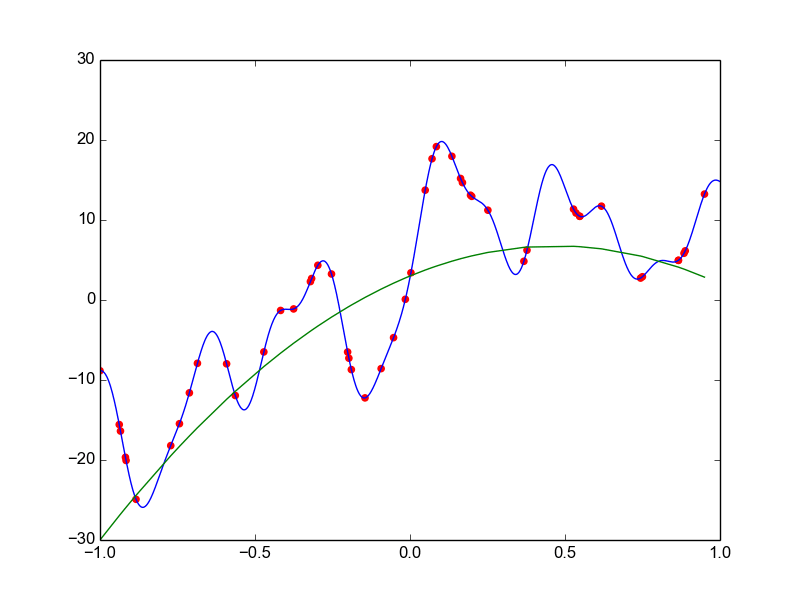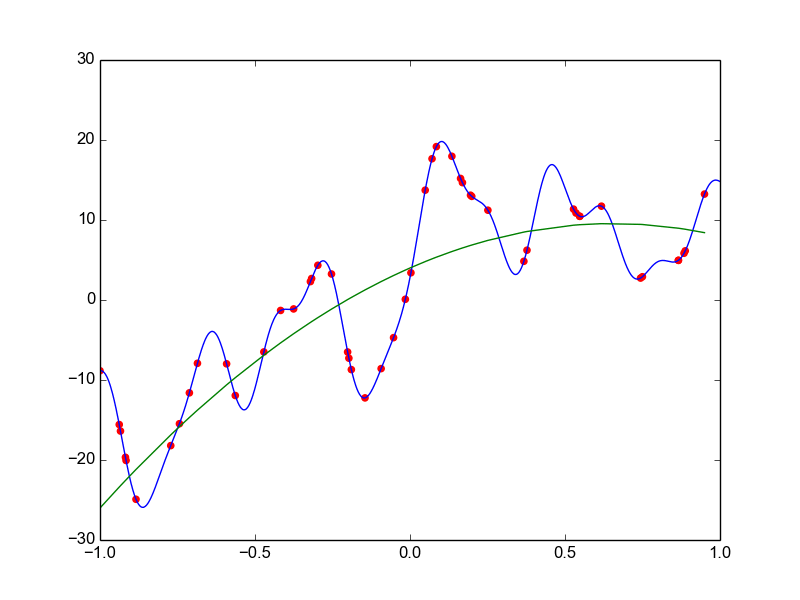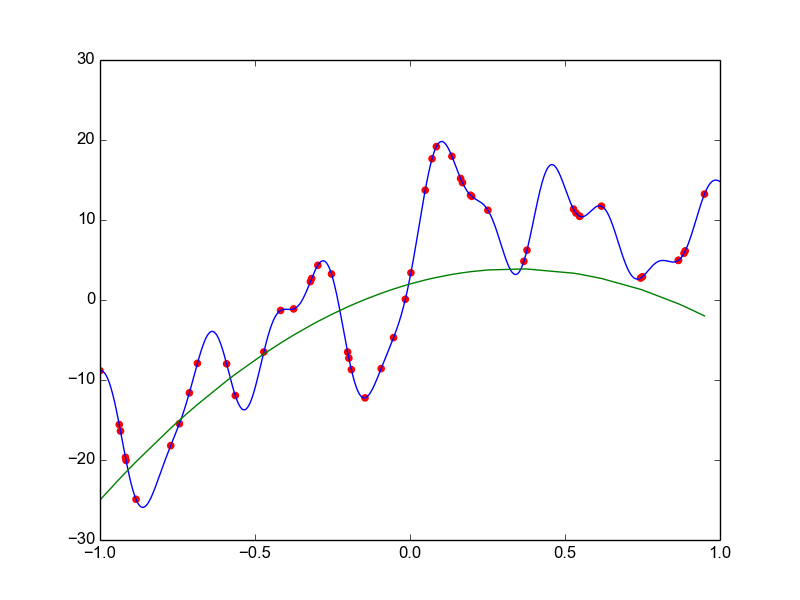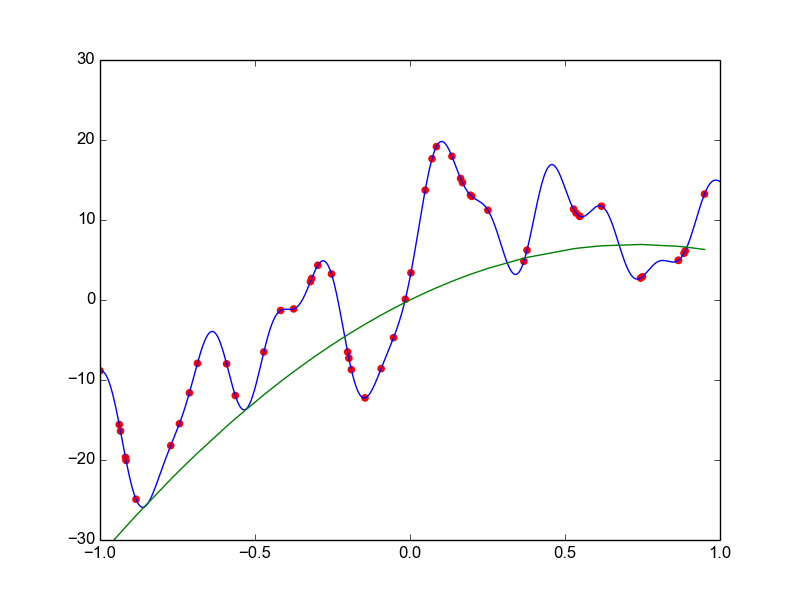
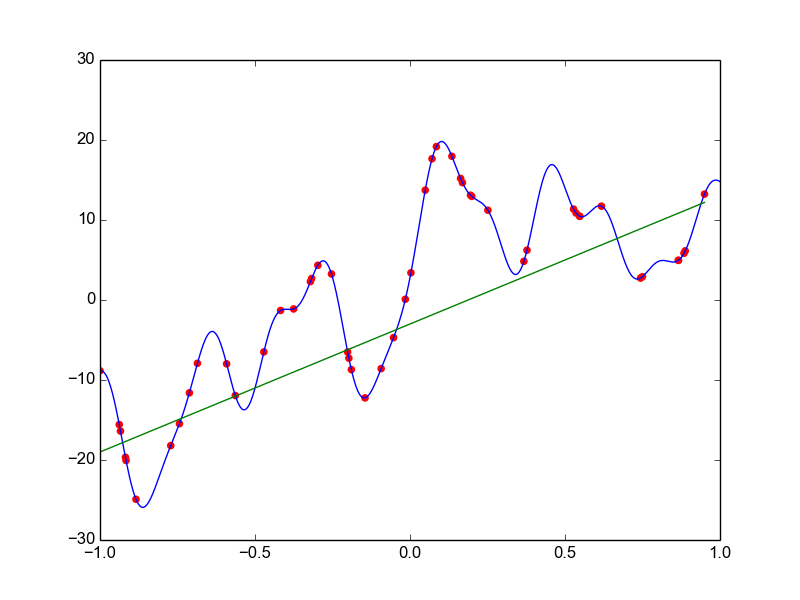
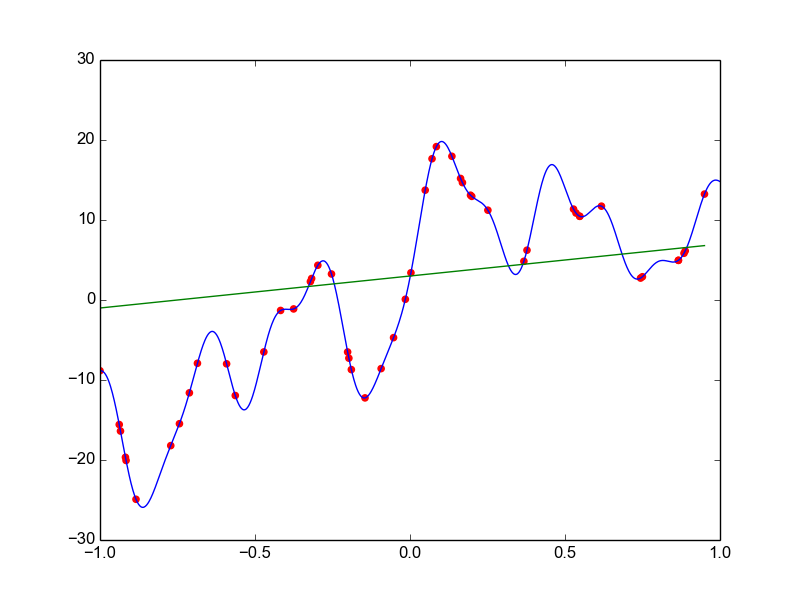
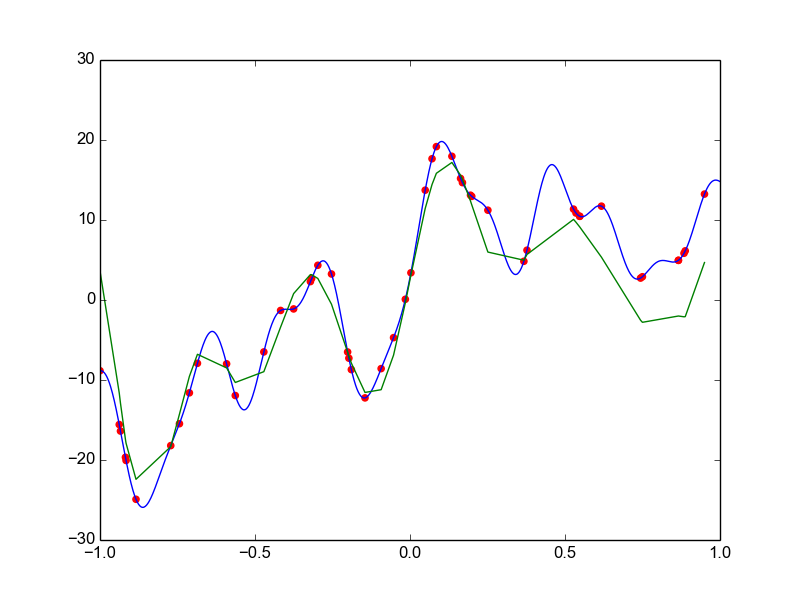
Models
Why not just use a complex model always ?
(c) One Fourth Labs

\( \left [\begin{array}{lcr} 0.1\\ 0.2\\ 0.4\\ ....\\0.8 \end{array} \right]\)
\( \left [\begin{array}{lcr} 2.6\\ 2.4\\ 3.1\\ ....\\4.1 \end{array} \right]\)
\( x \)
\( y \)
\( y = mx + c \) [true function, simple]
\(\hat{y} = ax^{100} + bx^{99} + ... + c \)
[our approximation, very complex]
Later in this course
Bias-Variance Tradeoff
Overfitting
Regularization
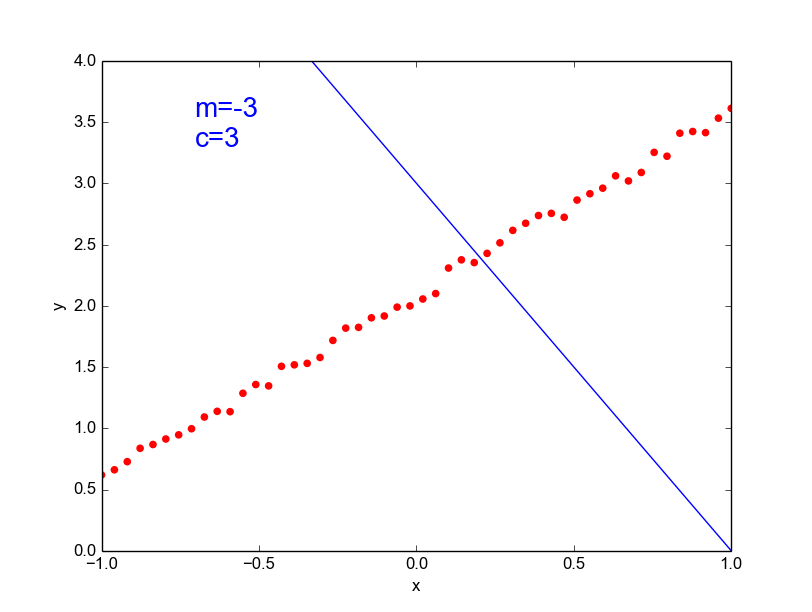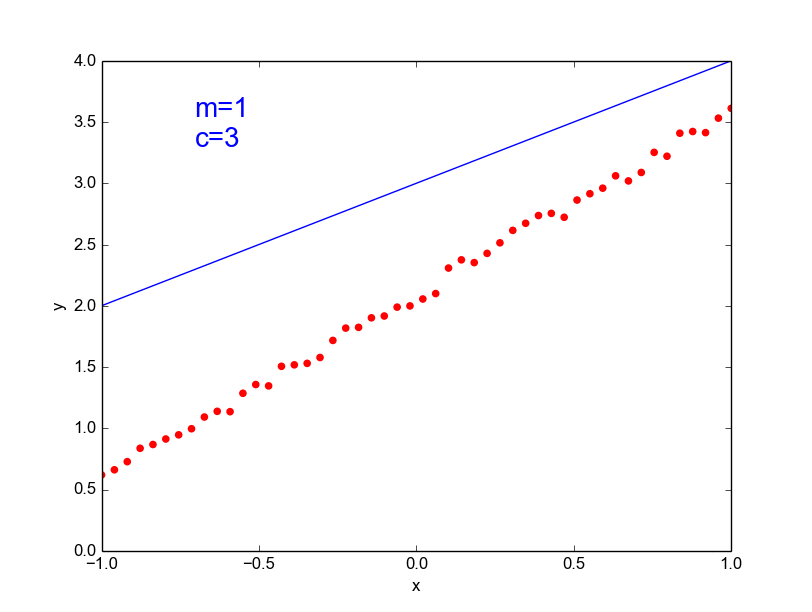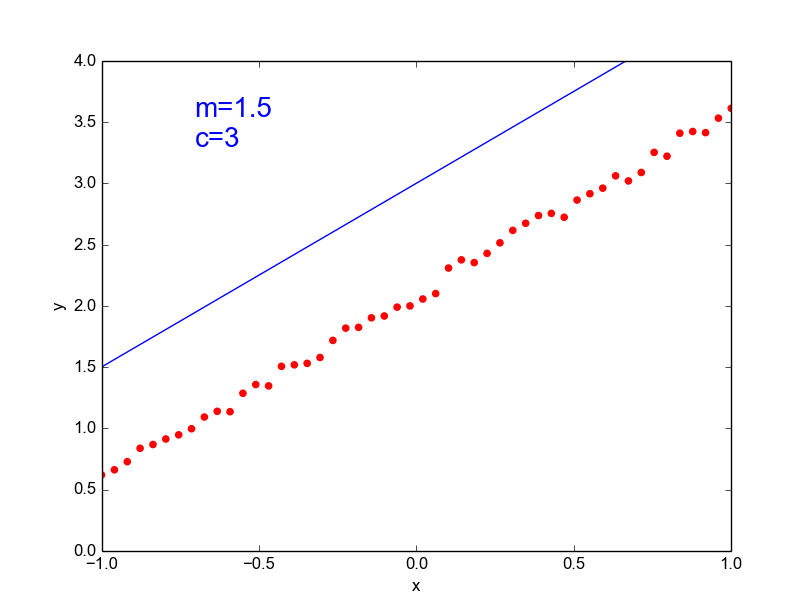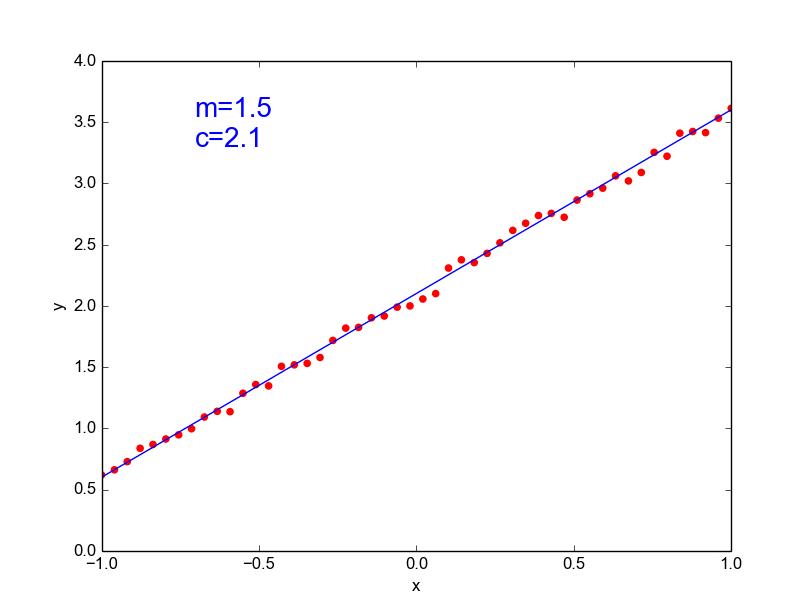


Models
What are the choices for \( \hat{f} \) ?
(c) One Fourth Labs

Model
Data


Task

Loss Function
How do we know which model is better ?

\( \left [\begin{array}{lcr} 0.00\\ 0.10\\ 0.20\\ ....\\6.40 \end{array} \right]\)
\( \left [\begin{array}{lcr} 0.24\\ 0.08\\ 0.12\\ ....\\0.36 \end{array} \right]\)
\( x \)
\( y \)
?
\( \hat{f_1}(x) \)
\( \left [\begin{array}{lcr} 0.25\\ 0.09\\ 0.11\\ ....\\0.36 \end{array} \right]\)
\( \left [\begin{array}{lcr} 0.32\\ 0.30\\ 0.31\\ ....\\0.22 \end{array} \right]\)
\( \left [\begin{array}{lcr} 0.08\\ 0.20\\ 0.14\\ ....\\0.15 \end{array} \right]\)
\( \hat{f_1}(x) = 1.79x^{25} - 4.54 x^{24} + ... - 1.48x + 2.48 \)
\( \hat{f_2}(x) = 2.27x^{25} + 9.89x^{24} + ... + 2.79x + 3.22 \)
\( \hat{f_3}(x) = 3.78x^{25} + 1.57x^{24} + ... + 1.01x + 8.68 \)
\( \begin{array}{lcr} 1\\ 2\\ 3\\ ....\\n \end{array} \)
\( \mathscr{L}_1 = \sum_{i=1}^{n} (y_i - \hat{f}_1(x_i))^2 \)
\( \hat{f_2}(x) \)
\( \hat{f_3}(x) \)
\( \mathscr{L}_2 = \sum_{i=1}^{n} (y_i - \hat{f}_2(x_i))^2 \)
\( \mathscr{L}_3 = \sum_{i=1}^{n} (y_i - \hat{f}_3(x_i))^2 \)
True Function
\( \hat{f_1}(x) \)


\( \hat{f_2}(x) \)
\( \hat{f_3}(x) \)









why not use numbers ?
whose function is better?
?




Loss Function
How do we know which model is better ?
(c) One Fourth Labs

\( \mathscr{L}_1 = \sum_{i=1}^{n} (y_i - \hat{f}_1(x_i))^2 = ? \)
\( \mathscr{L}_2 = \sum_{i=1}^{n} (y_i - \hat{f}_2(x_i))^2 = 2.02\)
\( \mathscr{L}_3 = \sum_{i=1}^{n} (y_i - \hat{f}_3(x_i))^2 = 2.34 \)
In this course
Square Error Loss
Cross Entropy Loss
KL divergence



\( \left [\begin{array}{lcr} 0.00\\ 0.10\\ 0.20\\ ....\\6.40 \end{array} \right]\)
\( \left [\begin{array}{lcr} 0.24\\ 0.08\\ 0.12\\ ....\\0.36 \end{array} \right]\)
\( x \)
\( y \)
\( \hat{f_1}(x) \)
\( \left [\begin{array}{lcr} 0.25\\ 0.09\\ 0.11\\ ....\\0.36 \end{array} \right]\)
\( \left [\begin{array}{lcr} 0.32\\ 0.30\\ 0.31\\ ....\\0.22 \end{array} \right]\)
\( \left [\begin{array}{lcr} 0.08\\ 0.20\\ 0.14\\ ....\\0.15 \end{array} \right]\)
\( \begin{array}{lcr} 1\\ 2\\ 3\\ ....\\n \end{array} \)
\( \hat{f_2}(x) \)
\( \hat{f_3}(x) \)
\( \mathscr{L}_1 = \sum_{i=1}^{n} (y_i - \hat{f}_1(x_i))^2 \)
\( = (0.24-0.25)^2 + (0.08-0.09)^2 + \newline (0.12-0.11)^2 + ... + (0.36-0.36)^2 \)
\( = 1.38 \)
\( \mathscr{L}_1 = \sum_{i=1}^{n} (y_i - \hat{f}_1(x_i))^2 = 1.38\)
\( \mathscr{L}_1 = \sum_{i=1}^{n} (y_i - \hat{f}_1(x_i))^2 = ? \)
Loss Function
What does a loss function look like ?
(c) One Fourth Labs

Loss
Model
Data


Task


Learning Algorithm
How do we identify parameters of the model?
(c) One Fourth Labs

\( \hat{f_1}(x) = 3.5x_1^2 + 2.5x_2^{3} + 1.2x_3^{2} \)
\( \hat{f_1}(x) = ax_1^2 + bx_2^{3} + cx_3^{2} \)
\( \mathscr{L}_1 = \sum_{i=1}^{n} (y_i - \hat{f}_1(x_i))^2 \)
| Budget in (100crs) |
Box Office Collection in (100 crs) | Action Scene in times (100 mins) | IMDB Rating |
|---|---|---|---|
| 0.55 | 0.66 | 0.22 | 4.8 |
| 0.68 | 0.91 | 0.77 | 7.2 |
| 0.66 | 0.88 | 0.67 | 6.7 |
| 0.72 | 0.94 | 0.97 | 8.1 |
| 0.58 | 0.74 | 0.35 | 5.3 |


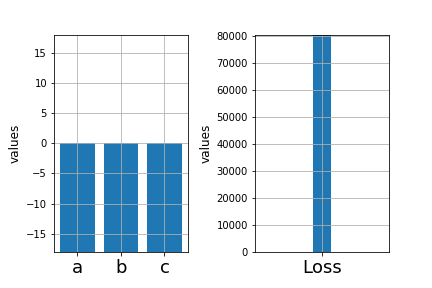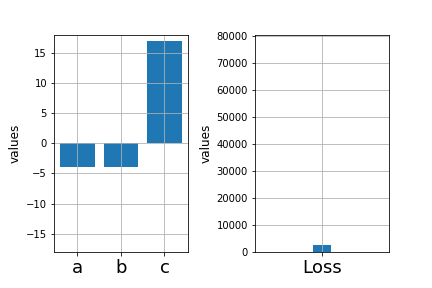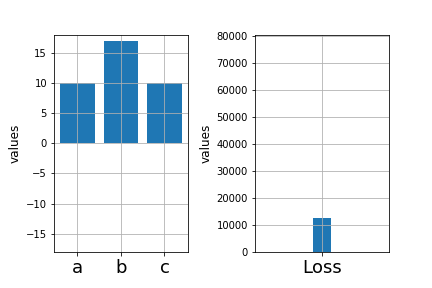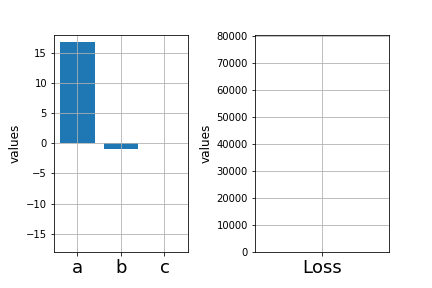
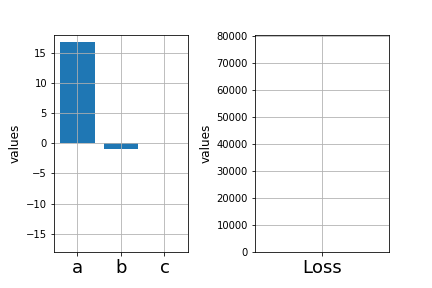



Learning Algorithm
How do you formulate this mathematically ?
(c) One Fourth Labs

\( \mathscr{L}_1 = \sum_{i=1}^{n} (y_i - \hat{f}_1(x_i))^2 \)
In practice, brute force search is infeasible
Find \(a, b, c \) such that
is minimized
\( \hat{f_1}(x) = ax_1^2 + bx_2^{3} + cx_3^{2} \)

| Budget (100crore) |
Box Office Collection(100 crore) | Action Scene times (100 mins) | IMDB Rating |
|---|---|---|---|
| 0.55 | 0.66 | 0.22 | 4.8 |
| 0.68 | 0.91 | 0.77 | 7,2 |
| 0.66 | 0.88 | 0.67 | 6.7 |
| 0.72 | 0.94 | 0.97 | 8.1 |
| 0.58 | 0.74 | 0.35 | 5.3 |


Learning Algorithm
How do you formulate this mathematically ?
(c) One Fourth Labs

\( \mathscr{L}_1 = \sum_{i=1}^{n} (y_i - \hat{f}_1(x_i))^2 \)
Many optimization solvers are available
\(min_{a,b,c}\)
\( \hat{f_1}(x) = ax_1^2 + bx_2^{3} + cx_3^{2} \)

| Budget (100crore) |
Box Office Collection(100 crore) | Action Scene times (100 mins) | IMDB Rating |
|---|---|---|---|
| 0.55 | 0.66 | 0.22 | 4.8 |
| 0.68 | 0.91 | 0.77 | 7,2 |
| 0.66 | 0.88 | 0.67 | 6.7 |
| 0.72 | 0.94 | 0.97 | 8.1 |
| 0.58 | 0.74 | 0.35 | 5.3 |


Learning Algorithm
How do you formulate this mathematically ?
(c) One Fourth Labs

\( \mathscr{L}_1 = \sum_{i=1}^{n} (y_i - \hat{f}_1(x_i))^2 \)
Many optimization solvers are available
\(min_{a,b,c}\)
\( \hat{f_1}(x) = ax_1^2 + bx_2^{3} + cx_3^{2} \)
In this course
Gradient Descent ++
Adagrad
RMSProp
Adam
| Budget (100crore) |
Box Office Collection(100 crore) | Action Scene times (100 mins) | IMDB Rating |
|---|---|---|---|
| 0.55 | 0.66 | 0.22 | 4.8 |
| 0.68 | 0.91 | 0.77 | 7,2 |
| 0.66 | 0.88 | 0.67 | 6.7 |
| 0.72 | 0.94 | 0.97 | 8.1 |
| 0.58 | 0.74 | 0.35 | 5.3 |
(c) One Fourth Labs

Learning Algorithm
How do you formulate this mathematically ?
Learning
Loss
Model
Data


Task



Evaluation
How do we compute a score for our ML model?
(c) One Fourth Labs

\( \left[\begin{array}{lcr} 2.1, 1.2, \dots, 5.6, 7.8 \end{array} \right]\)
\( \left[\begin{array}{lcr} 3.5, 6.6, \dots, 2.5, 6.3 \end{array} \right]\)



\( \left[\begin{array}{lcr} 6.3, 2.6, \dots, 4.5, 3.8 \end{array} \right]\)

\( \left[\begin{array}{lcr} 2.8, 3.6, \dots, 7.5, 2.1 \end{array} \right]\)

\( \left[\begin{array}{lcr} 6.3, 2.6, \dots, 4.5, 3.8 \end{array} \right]\)
True Labels
Predicted Labels
1
2
3
4
5
5
4
1
3
1
| Class Labels | |
|---|---|
| Lion | 1 |
| Tiger | 2 |
| Cat | 3 |
| Giraffe | 4 |
| Dog | 5 |


\( \left[\begin{array}{lcr} 1.9, 3.3, \dots, 4.2, 1.1 \end{array} \right]\)
\( \left[\begin{array}{lcr} 2.2, 1.7, \dots, 2.5, 1.8 \end{array} \right]\)
3
5
2
5
Top - 1
Evaluation
How do we compute a score for our ML model?
(c) One Fourth Labs

\( \left[\begin{array}{lcr} 2.1, 1.2, \dots, 5.6, 7.8 \end{array} \right]\)
\( \left[\begin{array}{lcr} 3.5, 6.6, \dots, 2.5, 6.3 \end{array} \right]\)



\( \left[\begin{array}{lcr} 6.3, 2.6, \dots, 4.5, 3.8 \end{array} \right]\)

\( \left[\begin{array}{lcr} 2.8, 3.6, \dots, 7.5, 2.1 \end{array} \right]\)

\( \left[\begin{array}{lcr} 6.3, 2.6, \dots, 4.5, 3.8 \end{array} \right]\)
True Labels
Predicted Labels
1
2
3
4
5
| Class Labels | |
|---|---|
| Lion | 1 |
| Tiger | 2 |
| Cat | 3 |
| Giraffe | 4 |
| Dog | 5 |


\( \left[\begin{array}{lcr} 1.9, 3.3, \dots, 4.2, 1.1 \end{array} \right]\)
\( \left[\begin{array}{lcr} 2.2, 1.7, \dots, 2.5, 1.8 \end{array} \right]\)
3
5
Top - 3
\( \left[\begin{array}{lcr} 1, 2, 3\end{array} \right]\)
\( \left[\begin{array}{lcr} 1, 2, 3\end{array} \right]\)
\( \left[\begin{array}{lcr} 1, 2, 3\end{array} \right]\)
\( \left[\begin{array}{lcr} 4, 5, 3\end{array} \right]\)
\( \left[\begin{array}{lcr} 5, 2, 1\end{array} \right]\)
\( \left[\begin{array}{lcr} 2, 1, 4\end{array} \right]\)
\( \left[\begin{array}{lcr} 5, 4, 1\end{array} \right]\)
Evaluation
How is this different from loss function ?
(c) One Fourth Labs



Evaluation
Brake
/Go
Loss function

\( maximize \)

#( ) +

____________________
#( )

#( )
#( ) +
____________________
#( )

#( )
Evaluation
Should we learn and test on the same data?
(c) One Fourth Labs

\( \left[\begin{array}{lcr} 2.1, 1.2, \dots, 5.6, 7.8 \end{array} \right]\)
\( \left[\begin{array}{lcr} 3.5, 6.6, \dots, 2.5, 6.3 \end{array} \right]\)



\( \left[\begin{array}{lcr} 6.3, 2.6, \dots, 4.5, 3.8 \end{array} \right]\)

\( \left[\begin{array}{lcr} 2.8, 3.6, \dots, 7.5, 2.1 \end{array} \right]\)
\( \left[\begin{array}{lcr} 2.2, 1.7, \dots, 2.5, 1.8 \end{array} \right]\)
1
2
3
4
2

\( \left[\begin{array}{lcr} 6.3, 2.6, \dots, 4.5, 3.8 \end{array} \right]\)
\( \left[\begin{array}{lcr} 2.8, 3.6, \dots, 7.5, 2.1 \end{array} \right]\)
\( \left[\begin{array}{lcr} 2.2, 1.7, \dots, 2.5, 1.8 \end{array} \right]\)
1
3
4



Training Data
Test Data
\( \mathscr{L}_1 = \sum_{i=1}^{n} (y_i - \hat{f}_1(x_i))^2 \)
\( \hat{f_1}(x) = ax_1^2 + bx_2^{3} + cx_3^{2} \)
\(min_{a,b,c}\)

Evaluation
How is this different from loss function ?
(c) One Fourth Labs

Learning
Loss
Model
Data


Task




Evaluation
Putting it all together
How does all the jargon fit into these jars?
(c) One Fourth Labs

Linear Algebra
Probability
Calculus






Data
Model
Loss
Learning
Task
Evaluation









Data, democratisation, devices
Why ML is very successful?
(c) One Fourth Labs







Data
Model
Loss
Learning
Task
Evaluation








Improvised
Democratised
Abundance


Typical ML effort
How to distribute your work through the six jars?
(c) One Fourth Labs

Your Job




Model
Loss
Learning
Evaluation






Data
Task


Mix and Match
Connecting to the Capstone
How to distribute your work through the six jars?
(c) One Fourth Labs


Mumbai





/
/
मुंबई \( \rightarrow \) Mumbai




\( \sum_{i=1}^{n} (y_i - \hat{f}(x_i))^2 \)
\( -\sum_{i=1}^{n} \log \hat{f}(x_i) \)
Accuracy
Precision/Recall
Top-k accuracy






Data
Model
Loss
Learning
Task
Evaluation







Assignment
How do you apply the six jars to a problem that you have encountered?
(c) One Fourth Labs

Explain the problem
Give link to the quiz
1. Formulate 3 problems from data.gov.in
2. In the dataturks labelled data, define tasks that you can perform and collect 10 data points for each
// Binary classification of whether there is text
// Detect text with bounding box - is accuracy easy to define here?
Copy of Final_1.3_Six_Elements_of_ML
By ananya_s_b
Copy of Final_1.3_Six_Elements_of_ML
- 846

