1.7 Sigmoid Neuron

The building block of Deep Neural Networks

Recap: Six jars

What we saw in the previous chapter?

(c) One Fourth Labs

Repeat the slide where we summarise the perceptron model in the context of the 6 jars.

Some thoughts on the contest

Just some ramblings!

(c) One Fourth Labs

We should create the binary classification monthly contest such that we can somehow visualize that the data is not linearly separable (don't know how)

 

We should also be able to visualize why the perceptron model is not fitting

 

Also give them some insights into what does the loss function indicate and how to make sense of it

Limitations of Perceptron

Can we plot the perceptron function ?

(c) One Fourth Labs

1. Show a training matrix with only 1 input (salary) and the decision is buy_car/not_buy_car

4. First only show x and y axis, label x axis as salary and y-axis as "\hat{y} = \hat{f}(salary)= perceptron(salary)"

5. Now take a positive point from the training data. Mark it on the x-axis and then mark the corresponding output for this point (+1)

6. Do this for a few points and then draw the step function

7, 8. Show the cartoon

 

9. Now on the x-axis show red and green regions for the positive and negative points

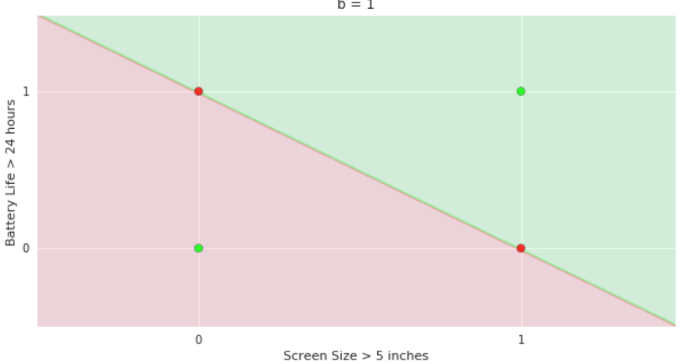
2. Show the perceptron model equations here

 

3. Suppose w=2, b =1 (comments for Mitesh: I took linearly separable data

7. Wait a minute!

8. Doesn't the perceptron divide the input space into positive and negative halves

Limitations of Perceptron

Can we plot the perceptron function ?

(c) One Fourth Labs

Wait a minute!

Salary ( in thousands) Can buy a car?
80 1
20 0
65 1
15 0
30 0
49 0
51 1
87 1

Doesn't the perceptron divide the input space into positive and negative halves ?

y=\sum_{i=1}^n w_i x_i \geq b
y=∑i=1nwixi≥b y=\sum_{i=1}^n w_i x_i \geq b
\text{Suppose,} \\ \mathbb{w_1} = 2,\\ \hspace{-0.2cm}\mathbb{b}\ \ = 1
Suppose,w1=2,b  =1\text{Suppose,} \\ \mathbb{w_1} = 2,\\ \hspace{-0.2cm}\mathbb{b}\ \ = 1

Limitations of Perceptron

How does the perceptron function look in 2 dimensions?

(c) One Fourth Labs

1. Show a training matrix with only 2 inputs (salary, family size) and the decision is buy_car/not_buy_car

4. First only show x1, x2 and y axis, label x1 axis as salary, x2 axis as family size and y-axis as "\hat{y} = \hat{f}(salary, size)= perceptron(salary, size)"

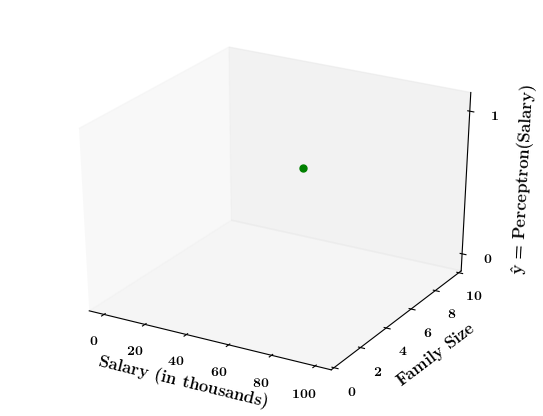
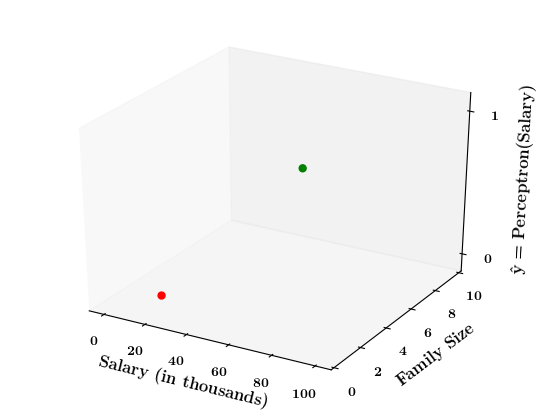
5. Now take a positive point from the training data. Mark it on the x1,x2-plane and then mark the corresponding output for this point (+1)

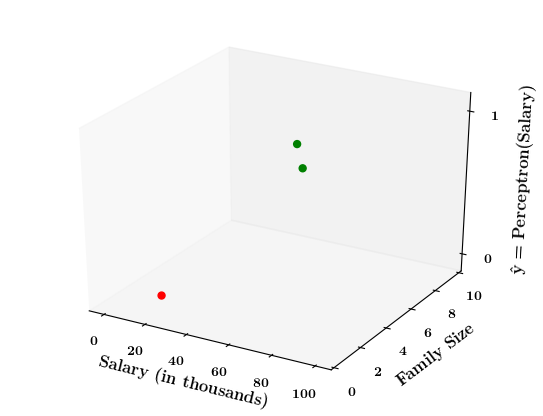
6. Do this for a few points and then draw the 2d - step function

7. Now on the x1, x2 plane show red and green regions for the positive and negative points an show that the line which is the foot of the step function which divides the space into two halves

2. Show the perceptron model equations here

 

3. Suppose w_1=<some_value>, w_2=<some_value>, b =1

Limitations of Perceptron

How does the perceptron function look in 2 dimensions?

(c) One Fourth Labs

y=\sum_{i=1}^n w_i x_i \geq b
y=∑i=1nwixi≥b y=\sum_{i=1}^n w_i x_i \geq b
\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.1 \\ \mathbb{b} = -10.5
Suppose,w1=0.2,w2=0.1b=−10.5\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.1 \\ \mathbb{b} = -10.5
Salary (in thousands) Family size Can buy a car?
80 2 1
20 1 0
65 4 1
15 7 0
30 6 0
49 3 0
51 4 1
87 8 1

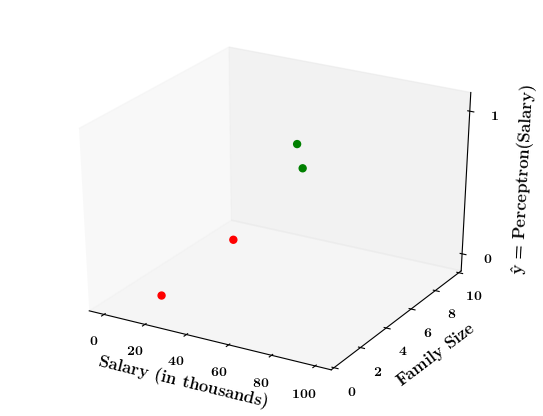
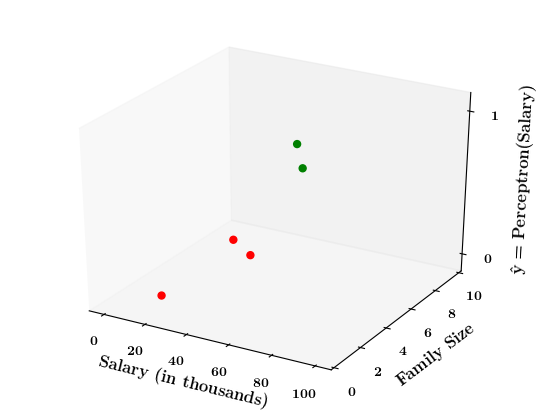
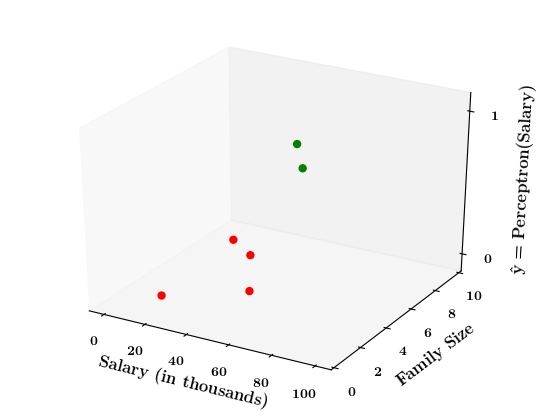
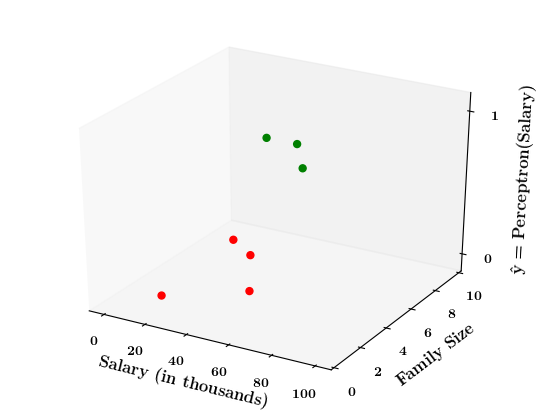
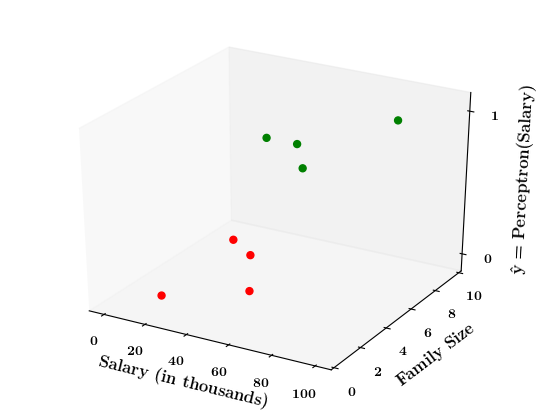
Limitations of Perceptron

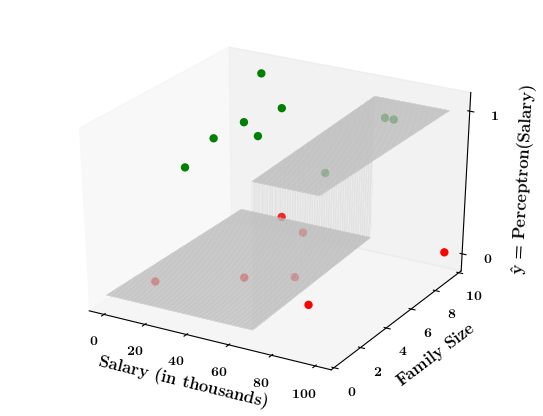
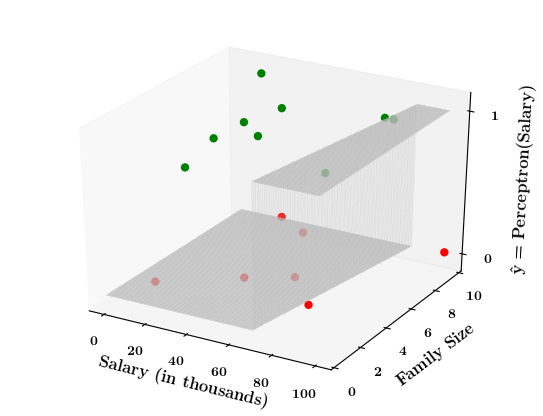
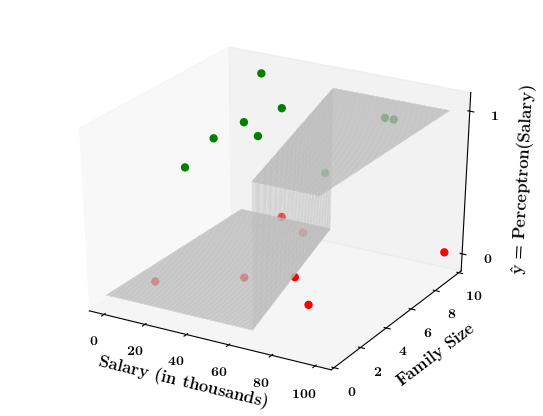
What if the data is not linearly separable ?

(c) One Fourth Labs

1. Show a training matrix with only 2 inputs (salary, family size) and the decision is buy_car/not_buy_car

Now on the x1. x2 plane show some data which is not linearly separable

 

Adjust the perceptron function and show that no matter what you do some green points will go to the other side or some red points will go to the other side. 

2. Show the perceptron model equations here

 

3. Suppose w_1=<some_value>, w_2=<some_value>, b =1

Limitations of Perceptron

What if the data is not linearly separable ?

(c) One Fourth Labs

y=\sum_{i=1}^n w_i x_i \geq b
y=∑i=1nwixi≥b y=\sum_{i=1}^n w_i x_i \geq b
\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.1 \\ \mathbb{b} = -6
Suppose,w1=0.2,w2=0.1b=−6\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.1 \\ \mathbb{b} = -6
Salary (in thousands) Family size Can buy a car?
81 8 1
37 9 0
34 5 1
... ... ...
40 4 0
100 10 0
10 10 1
85 8 1
\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.1 \\ \mathbb{b} = -3
Suppose,w1=0.2,w2=0.1b=−3\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.1 \\ \mathbb{b} = -3
\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = -0.3 \\ \mathbb{b} = -14
Suppose,w1=0.2,w2=−0.3b=−14\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = -0.3 \\ \mathbb{b} = -14
\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = -0.5 \\ \mathbb{b} = -14
Suppose,w1=0.2,w2=−0.5b=−14\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = -0.5 \\ \mathbb{b} = -14
\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.1 \\ \mathbb{b} = -9
Suppose,w1=0.2,w2=0.1b=−9\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.1 \\ \mathbb{b} = -9
\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.1 \\ \mathbb{b} = -14
Suppose,w1=0.2,w2=0.1b=−14\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.1 \\ \mathbb{b} = -14
\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = -0.7 \\ \mathbb{b} = -14
Suppose,w1=0.2,w2=−0.7b=−14\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = -0.7 \\ \mathbb{b} = -14
\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.3 \\ \mathbb{b} = -14
Suppose,w1=0.2,w2=0.3b=−14\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.3 \\ \mathbb{b} = -14
\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.7 \\ \mathbb{b} = -14
Suppose,w1=0.2,w2=0.7b=−14\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.7 \\ \mathbb{b} = -14

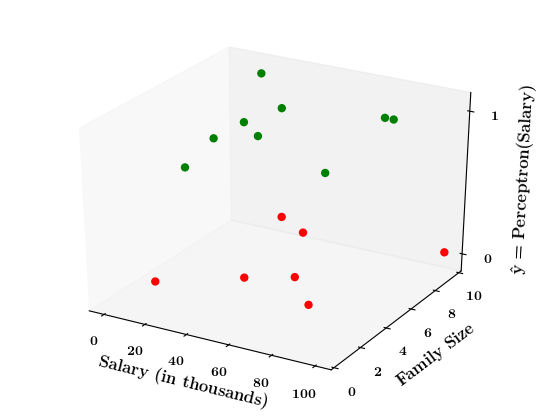
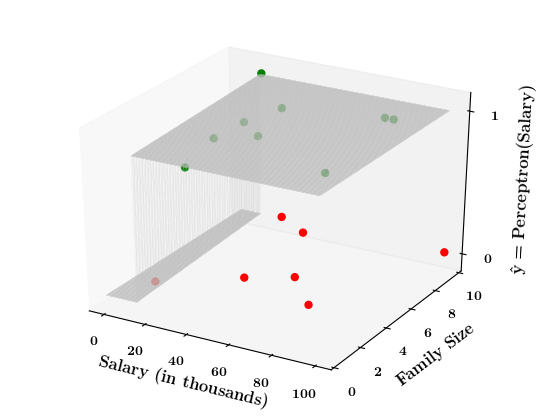
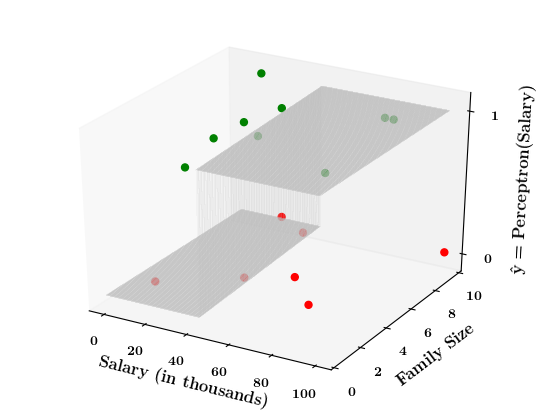
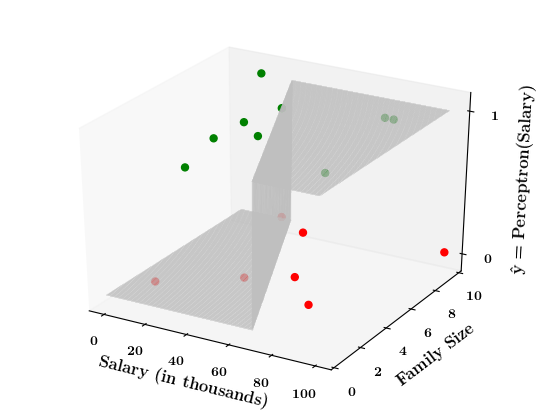
Limitations of Perceptron

Isn't the perceptron model a bit harsh at the boundaries ?

(c) One Fourth Labs

Repeat the training data with one input (salary)

Show the 2d plot from before

 

2. Now show the cartoon

 Show the perceptron model equations here

 

Suppose w_1=<some_value>, w_2=<some_value>, b =1

Isn't it a bit odd that a person with 150K salary will but a car but someone with 150.1K will not buy a car ?

Limitations of Perceptron

Isn't the perceptron model a bit harsh at the boundaries ?

(c) One Fourth Labs

Isn't it a bit odd that a person with 50.1K salary will buy a car but someone with 49.9K will not buy a car ?

Salary ( in thousands) Can buy a car?
80 1
20 0
65 1
15 0
30 0
49 0
51 1
87 1
y=\sum_{i=1}^n w_i x_i \geq b
y=∑i=1nwixi≥b y=\sum_{i=1}^n w_i x_i \geq b
\text{Suppose,} \\ \mathbb{w_1} = 2,\\ \hspace{-0.2cm}\mathbb{b}\ \ = 1
Suppose,w1=2,b  =1\text{Suppose,} \\ \mathbb{w_1} = 2,\\ \hspace{-0.2cm}\mathbb{b}\ \ = 1

The Road Ahead

What's going to change now ?

(c) One Fourth Labs

Show the six jars and convey the following by animation

-- Boolean output gets replaced by real output

-- "specific learning algo" gets replaced by "a more generic learning algorithm"

-- "harsh at boundaries gets replaced by smooth at boundaries

-- "Linear" gets replaced by non-linear

Harsh at boundaries

Linear

Real inputs

Boolean output

Specific learning algorithm

(c) One Fourth Labs

The Road Ahead

What's going to change now ?

(c) One Fourth Labs

\( \{0, 1\} \)

Boolean

Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}
Accuracy=Number of correct predictionsTotal number of predictionsAccuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

Loss

Model

Data

Task

Evaluation

Learning

Linear

Real inputs

Boolean output

loss = \sum_i max(0,1-y_i*\hat{y_i})
loss=∑imax(0,1−yi∗yi^)loss = \sum_i max(0,1-y_i*\hat{y_i})

Specific learning algorithm

Harsh at boundaries

Real output

Non-linear

A more generic learning algorithm

Smooth at boundaries

Data and Task

What kind of data and tasks can Perceptron process ?

(c) One Fourth Labs

Same mobile phone dataset from before.

Real inputs

Data and Task

What kind of data and tasks can Perceptron process ?

(c) One Fourth Labs

Data and Task

What kind of data and tasks can Perceptron process ?

(c) One Fourth Labs

Real inputs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size (inches) 5.8 6.18 5.84 6.2 5.9 6.26 4.7 6.41 5.5
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 3060 3500 3060 5000 3000 4000 1960 3700 3260
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0

Model

Can we have a smoother (not-so-harsh) function ?

(c) One Fourth Labs

1) Show step function first and then super-impose the sigmoid function

 

2) Show the equation

 

3) Now on the RHS below the equation, substitute some values for wx+b and show the output on the plot (basically, I want to tell people that don't get overwhelmed when you see a function, just susbstitute some values in it and see how the plot looks, 0,1,-1, \inf, -inf

 

 

 

Show the sigmoid function equation here

Model

What happens when we have more than 1 input ?

(c) One Fourth Labs

1) Show the same phone data from before

 

2) Now show an image of sigmoid model with the equation containing \sum_w_i x_i + b

 

3) Now replace the summation by w^Tx

 

4) How do you plot this function: on x-axis show w^tx +b and on y-axis show the output y (again plot for different values of  w^tx +b)

 

 

 

Show the sigmoid function equation here

Model

How does this help when the data is not linearly separable ?

(c) One Fourth Labs

Still does not completely solve our problem but we will slowly get there!

1. Show a training matrix with only 2 inputs (salary, family size) and the decision is buy_car/not_buy_car

1. In the first case we will consider data which only ha problems at the boundary (meaning that only at the boundary around wx+b = 0 some green and red points mix with each other)

 

2. Now show that unlike the perceptron which was either misclassifying the positive or negative points, sigmoid gives a soft decision 

 

3. also show that by adjusting w_1 and w_2 you can accommodate for different types of boundary cases (please take Gokul's help for these plots)

2. Show the sigmoid model equations here

 

 

Model

What about extreme non-linearity ?

(c) One Fourth Labs

Still does not completely solve our problem but we will slowly get there with more complex models!

1. Show a training matrix with only 2 inputs (salary, family size) and the decision is buy_car/not_buy_car

1.Now show a case where the blue and red points are completely mixed with each other

 

2. show that no matter how you adjust w_1 and w_2 you will not be able to find any separation between blue and red points

 

3. Now show the quote at RHS bottom using our cartoon person

2. Show the sigmoid model equations here

 

 

Model

How does the function behave when we change w and b

(c) One Fourth Labs

5. Cartoon person: At what value of x is the value of sigmoid(X) = 0.5

2. Show a scale here for w and b

 

 

 

1. Show the sigmoid function here (the x-axis is x and y -asix is sigmoid(x)

 

3. CHange the value of w below and show how the plot changes

 

4. Now change the value of w below and show how the plot changes

 

5. Show the cartoon person woth the W

 

6. the derivation

2. Show the sigmoid model equations here

 

 

the derivation to show that sigm(x) = 0.5 at  x = -b/w  

 

Loss Function

What is the loss function that you use for this model ?

(c) One Fourth Labs

1. Show small training matrix here

2. On RHS show the model equation an y_hat = sigmoid

3. Show an empty column for y_hat now and then add entries in it (numbers between 0 and 1)

4. Now on RHS below the model equations show the equation for sqaured error loss

5. Now using the cartoon person show that we can use even better loss functions in this case but we will see that later in the course.

Learning Algorithm

 

Can we try to estimate w, b using some guess work ?

(c) One Fourth Labs

Initialise 

1. Show training matrix with 1 inputs and one output and a total of 5 such points

 

2. On the LHS first show the algorithm as it appears now except that instead of w1,w2,b we will only have w, b

 

3. Now replace the two lines L = and update by a signle line guess_and_update(w, b)

2. on LHS show the box containing w1, w2, b

 

4. Now plot these points as x,y pairs in the corner below

 

5. Iniitialize w,b to some values such that the points do not fit very well

 

6. Now goe over the points one by and and intelligently move w and b so that the points slowly start coming closer to the function (I should be able to say that earlier in 5.5 we saw that if we increase w something happens and if we increase b something happens so I am just using that intuition to slowly adjust w and b 

 

\(w_1, w_2, b \)

Iterate over data:

\( \mathscr{L}  = compute\_loss(x_i) \)

\( update(w_1, w_2, b, \mathscr{L}) \)

till satisfied

Sigmoid equation here

Learning Algorithm

 

Can we take a closer look at what we just did ?

(c) One Fourth Labs

Initialise 

1. Start with the same algo as on previous slide

 

2. Replace guess_and_update by w = w+\delat w and b = b + \delata b

 

3. In this box now show the plot again containing all the points and show how you were going over them one by one in the algo on LHS

 

4. now below this box, write \delta w= some_guess, \deltab = some_guess

\(w_1, w_2, b \)

Iterate over data:

\( \mathscr{L}  = compute\_loss(x_i) \)

\( update(w_1, w_2, b, \mathscr{L}) \)

till satisfied

Learning Algorithm

 

Can we connect this to the loss function ?

(c) One Fourth Labs

Initialise 

0. Same algo as on previous slide

 

1. Show a table containing iteration number, w, b, loss

 

2. In this black box show the plot again

 

3. Now sync the table and the plot such that you show the w,b value in the table at the end of each iteration and show how the corresponding loss looks like and how the plot looks like

 

4. In apink box below say "Indeed we were using the loss function to guide us in finding \delta w and \delta b

\(w_1, w_2, b \)

Iterate over data:

\( \mathscr{L}  = compute\_loss(x_i) \)

\( update(w_1, w_2, b, \mathscr{L}) \)

till satisfied

Learning Algorithm

 

Can we visualise this better ?

(c) One Fourth Labs

Initialise 

0. Same algo as on previous slide

 

1. Same stuff as the previous slide except that now instead of the table we will have a 3d plot for loss v/s w,b

 

2. first just show the 3 axes so that I can talk through them and explain what each axes means

 

3. now plot the error surface (use different colors than what we use in the course, also make the surface a bit more transparent

 

4. now show what happens as you change the value of w,b in each iteration

\(w_1, w_2, b \)

Iterate over data:

\( \mathscr{L}  = compute\_loss(x_i) \)

\( update(w_1, w_2, b, \mathscr{L}) \)

till satisfied

Learning Algorithm

 

What is our aim now ?

(c) One Fourth Labs

Initialise 

1. Start with the same algo as on previous slide

 

2. Replace guess_and_update by w = w+\delat w and b = b + \delata b

 

3. In this box now show the plot again containing all the points and show how you were going over them one by one in the algo on LHS

 

4. now below this box, write \delta w= some_guess, \deltab = some_guess

\(w_1, w_2, b \)

Iterate over data:

\( \mathscr{L}  = compute\_loss(x_i) \)

\( update(w_1, w_2, b, \mathscr{L}) \)

till satisfied

Show a quote here which says that

 

"Instead of guessing \delta w and \delta b, we need a principled way of changing w and b based on the loss function"

Learning Algorithm

 

Can we formulate this more mathematically ?

(c) One Fourth Labs

This slide will be the same as slide 27 of lecture 3, without any of the text on the slide (just the equations and the diagrams) 

Show a quote here which says that

 

"Instead of guessing \delta w and \delta b, we need a principled way of changing w and b based on the loss function"

Learning Algorithm

 

Can we get the answer from some basic mathematics ?

(c) One Fourth Labs

1. Show the 2 equations for w and L(w) on the LHS in big font

 

2. Now show Taylor series equation on RHS for the scalar case

 

3. Now on the LHS add b also so that we have L(w,b)

 

4. Now below these equations show that \theta = [w, b] and in the loss equations replace w,b by \theta

 

5. Now show the Taylor series formula for the scalar case

w --> w + \eta \delta w

 

b --> b + \eta \delta b

 

L(w) < L(w +\eta \delta w)

 

L(b) < L(b +\eta \delta b)

Leave this space empty for me to do some pen work

 

I will talk about derivatives and partial derivatives and gradients

Learning Algorithm

 

How does Taylor series help us to arrive at the answer ?

(c) One Fourth Labs

Slides 28, 29, 30 from my lecture 3

Learning Algorithm

 

How does the algorithm look like now ?

(c) One Fourth Labs

Initialise 

\(w_1, w_2, b \)

Iterate over data:

write update rule here

till satisfied

A cartoon person asking How do I compute \delta w and \delta b?

Learning Algorithm

 

How do I compute \deltaw and \delta b

(c) One Fourth Labs

Show plot here with the 5 points which need to be fitted from the earlier example*

*Refer to slide 32, 33, 34 from lecture 3 for reference

1. Write loss function as sum over 5 squared error terms

2. take derivative on both sides

3. move derivative into the sum

4. Now say we will consider only one term in this sum

 

Now on the next slide show the derivation from slide 33

 

Now on the next slide start from everything upto bullet point 4. Now show the formula for \delta w and \delta b as a summation of terms (similar to that on slide 34

Learning Algorithm

 

How does the full algorithm look like ?

(c) One Fourth Labs

*Refer to slide 32, 33, 34 from lecture 3 for reference

Repeat Slide 35 from my lecture

Learning Algorithm

 

What happens when we have more than 2 parameters ?

(c) One Fourth Labs

1. Show a dataset containing 5 input variables

 

2. Show the corresponding model equation

 

3. Now show the algorithm from before but now instead of update rules for w and b you will have update rules for w_1,...w_5 and b

 

4. Now show the equation for \delta_w and \delta_b from before

 

5. Now replace w by w_1 and x by x_1 in the formula for dL/dw (on the next slide have the full derivation)

 

6. Now say that in general dL/dw_1 = ....

 

Learning Algorithm

 

What happens when we have more than 2 parameters ?

(c) One Fourth Labs

Show the full derivation for dL/dw_1

Learning Algorithm

 

What happens when we have more than 2 parameters ?

(c) One Fourth Labs

Now take the slide 8.5 and modify it so that you have gradient descent code for 5 variables (the code has to be modularized and generalized for k variables)

 

It would be great if we can then convert the above code to vector form where we directly do everything in terms of \theta where \theta = [w1, w2, w3, w4, w5]

 

Now run the code and on the RHS show a plot of how the loss decreases with number of iterations

Evaluation

 

How do you check the performance of the sigmoid model?

(c) One Fourth Labs

Same slide as that in MP neuron

Take-aways

What are the new things that we learned in this module ?

(c) One Fourth Labs

Show the 6 jars at the top (again can be small)

 

\( \{0, 1\} \)

\( \in \mathbb{R} \)

Tasks with Real inputs and real outputs

show the sigmoid plot with the issue of non-linearly separable data

show squared error loss

show gradient descent update rule

show accuracy formula

Take-aways

What are the new things that we learned in this module ?

(c) One Fourth Labs

A slide where we compare sigmoid, perceptron and MP neuron in terms of 6 jars

 

Still not complex enough to handle non-linear data

Copy of Copy of 1.7 Sigmoid Neuron

By ananya_s_b

Source: Pritha Ganguly

Copy of Copy of 1.7 Sigmoid Neuron

  • 585

More from ananya_s_b