1.5 McCulloch Pitts Neuron

Your first model

Recap: Six jars

What we saw in the previous chapter?

(c) One Fourth Labs

Repeat slide 9.1 of the previous chapter

Artificial Neuron

What is the fundamental building block of Deep Learning ?

(c) One Fourth Labs

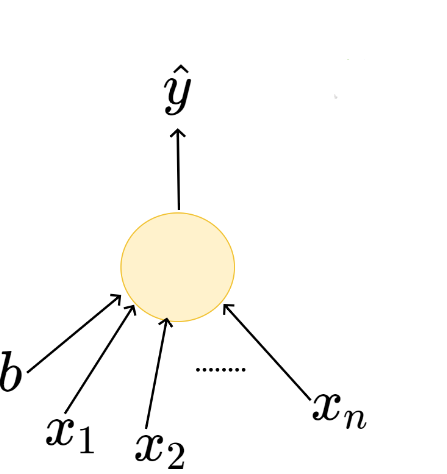
Show a single neuron taking 3 inputs and weights

Recall Biological Neuron

Where does the inspiration come from ?

(c) One Fourth Labs

Copy paste earlier slide on BN from history

The Model

When and who proposed this model ?

(c) One Fourth Labs

Show photos of both and write a short Bio of a few sentences

The Model

How are we going to approach this ?

(c) One Fourth Labs

Show the six jars and convey the following by animation

 

1) Focus on the model jar

2) then show an arrow to 1. Data jar, 2. task, 3. loss function, 4. algorithm

3) This will be a first programming assignment where you will use some of the Numpy basics

The Model

What is the mathematical model ?

(c) One Fourth Labs

1) Diagram

2) Show constrains on x,y (boolean)

3) Write the equations for f and g

4) The parameter is b

One parameter, b

Data and Task

What kind of data and tasks can MP neuron process ?

(c) One Fourth Labs

LHS  diagram with boolean input and outputs

 

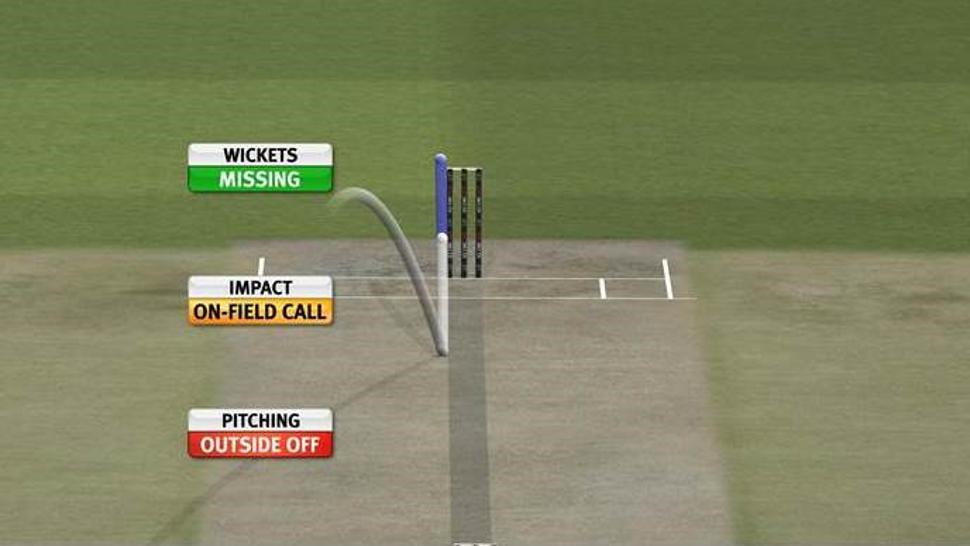
RHS data x (3 lbw variables: pitch, impact, missing stumps, show lbw DRS photo) and y (summation function to show lbw or not)

// threshold >= 3 

 

 

 

Data and Task

What kind of data and tasks can MP neuron process ?

Pitch
in line		 Impact Missing stumps Is it LBW? (y)
1 0 0 0
0 1 1 0
1 1 1 1
0 1 0 0

x1

(pitch)

x3

(stumps off)

x2

(impact)

y (LBW)

y=\sum_{i=1}^3 x_i \geq 3
y=∑i=13xi≥3y=\sum_{i=1}^3 x_i \geq 3

Data and Task

What kind of data and tasks can MP neuron process ?

Pitch
in line		 Impact Missing stumps Is it LBW? (y)
1 0 0 0
0 1 1 0
1 1 1 1
0 1 0 0

x1

(pitch)

x3

(stumps off)

x2

(impact)

y (LBW)

y=\sum_{i=1}^3 x_i \geq 3
y=∑i=13xi≥3y=\sum_{i=1}^3 x_i \geq 3

Data and Task

What kind of data and tasks can MP neuron process ?

(c) One Fourth Labs

A model of  MP Neuron with these input features

 

​Use b instead of \theta to be consistent with perceptron, sigmoid etc

Real world example with a recommender system

 

Purchase of smartphone: Have several (~ 10) boolean conditions such as screen size > 5 inch, etc. We have labelled data of the preference (yes/no) of a user across several (~ 100 smartphones). 

 

Ananya has collected this data

Boolean inputs

Boolean output

Data and Task

What kind of data and tasks can MP neuron process ?

(c) One Fourth Labs

Boolean inputs

Boolean output

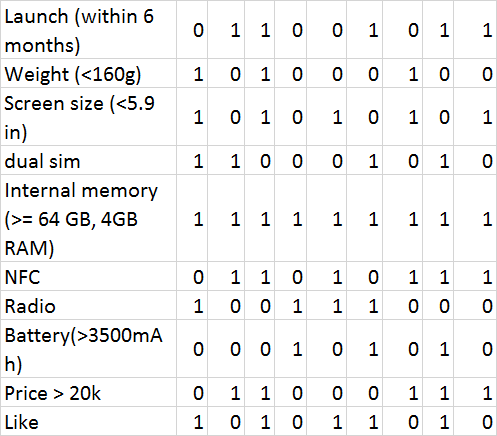
Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (<160g) 1 0 1 0 0 0 1 0 0
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0
Price > 20k 0 1 1 0 0 0 1 1 1
Like (y) 1 0 1 0 1 1 0 1 0

x1

xn

x2

y 

b

y=\sum_{i=1}^n x_i \geq b
y=∑i=1nxi≥by=\sum_{i=1}^n x_i \geq b

Data and Task

What kind of data and tasks can MP neuron process ?

(c) One Fourth Labs

Boolean inputs

Boolean output

x1

xn

x2

y 

b

y=\sum_{i=1}^n x_i \geq b
y=∑i=1nxi≥by=\sum_{i=1}^n x_i \geq b

Loss Function

Ho do we compute the loss ?

(c) One Fourth Labs

Same data matrix from before

 

Animation:

- Feed one input from the matrix to the model

- Highlight the true output y and predicted output y_hat (just variables, not actual values)

- Show simple equation y - \hat_y [I will explain while talking what this equation means]

- Now add summation over all i y_i - \hat_y_i

- Now add square

Same model diagram from before.

Show loss function here

Loss Function

Ho do we compute the loss ?

(c) One Fourth Labs

loss / error = y-\hat{y}
loss/error=y−y^loss / error = y-\hat{y}
Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (<160g) 1 0 1 0 0 0 1 0 0
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0
Price > 20k 0 1 1 0 0 0 1 1 1
Like (y) 1 0 1 0 1 1 0 1 0
\hat{y}
y^\hat{y}
x_1
x1x_1
x_2
x2x_2
x_n
xnx_n
b
bb
\hat{y}=\sum_{i=1}^n x_i \geq b
y^=∑i=1nxi≥b\hat{y}=\sum_{i=1}^n x_i \geq b

Loss Function

Ho do we compute the loss ?

(c) One Fourth Labs

loss = \sum_i y_i-\hat{y_i}
loss=∑iyi−yi^loss = \sum_i y_i-\hat{y_i}
loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2
\hat{y}
y^\hat{y}
x_1
x1x_1
x_2
x2x_2
x_n
xnx_n
b
bb
\hat{y}=\sum_{i=1}^n x_i \geq b
y^=∑i=1nxi≥b\hat{y}=\sum_{i=1}^n x_i \geq b
Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (<160g) 1 0 1 0 0 0 1 0 0
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0
Price > 20k 0 1 1 0 0 0 1 1 1
Like (y) 1 0 1 0 1 1 0 1 0

Loss Function

Ho do we compute the loss ?

(c) One Fourth Labs

loss = \sum_i y_i-\hat{y_i}
loss=∑iyi−yi^loss = \sum_i y_i-\hat{y_i}
\hat{y}
y^\hat{y}
x_1
x1x_1
x_2
x2x_2
x_n
xnx_n
b
bb
\hat{y}=\sum_{i=1}^n x_i \geq b
y^=∑i=1nxi≥b\hat{y}=\sum_{i=1}^n x_i \geq b
Launch (within 6 months) 0 1 1 0 0 1 0 1 1 0
Weight (<160g) 1 0 1 0 0 0 1 0 0 1
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1 0
dual sim 1 1 0 0 0 1 0 1 0 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1 0
NFC 0 1 1 0 1 0 1 1 1 0
Radio 1 0 0 1 1 1 0 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0 0
Price > 20k 0 1 1 0 0 0 1 1 1 0
Like?      (y) 1 0 1 0 1 1 0 1 0 0
predicted         1 0 0 1 1 1 1 0 0 0
loss 0 0 1 -1 0 0 -1 1 0 0
\hat{y}
y^\hat{y}

Loss Function

Why do we use the square of the error ?

(c) One Fourth Labs

Same data matrix from before

 

Animation:

- Remove the square

- Now add column for \hat_y such that there are equal number of positive and negative errors

- Now compute the loss function without the square

- now show what happens when you add the square

Same model diagram from before.

Show loss function here

Loss Function

Why do we use the square of the error ?

(c) One Fourth Labs

Same data matrix from before

 

Animation:

- Remove the square

- Now add column for \hat_y such that there are equal number of positive and negative errors

- Now compute the loss function without the square

- now show what happens when you add the square

Same model diagram from before.

Show loss function here

Loss Function

Ho do we compute the loss ?

(c) One Fourth Labs

Pitch
in line		 Impact Missing stumps Is it LBW? (y)
1 0 0 0
0 1 1 0
1 1 1 1
0 1 0 0

x1

(pitch)

x3

(stumps off)

x2

(impact)

(LBW)

loss / error = y-\hat{y}
loss/error=y−y^loss / error = y-\hat{y}
\hat{y}
y^\hat{y}

Loss Function

Ho do we compute the loss ?

(c) One Fourth Labs

Pitch
in line		 Impact Missing stumps Is it LBW? (y)
1 0 0 0
0 1 1 0
1 1 1 1
0 1 0 0

x1

(pitch)

x3

(stumps off)

x2

(impact)

(LBW)

loss = \sum_i y_i-\hat{y_i}
loss=∑iyi−yi^loss = \sum_i y_i-\hat{y_i}
\hat{y}
y^\hat{y}
loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2

Learning Algorithm

How do we train our model?

(c) One Fourth Labs

Same data matrix from before

 

Animation:

- Show the search logo first

- Now show the tick mark and the brute force message

- Now show the plot

- The y_hat column will change as you change the value of b 

Same model equations here

Show loss function here

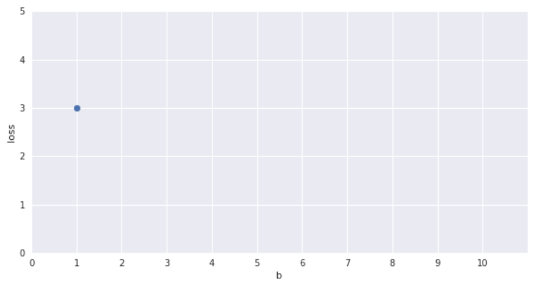
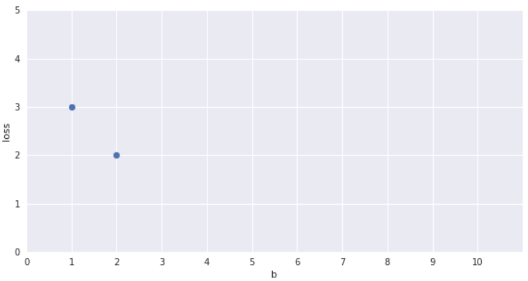
show a plot here of b on the x-axis and loss on the y axis and one-by-one fill the points in the plot for b = 1 to 10

for b=1 and b=2 the  y_hat column should get adjusted as you change the value of b (so that I can talk about how the loss was computed)

Only one parameter, can afford Brute Force search

Learning Algorithm

How do we train our model?

(c) One Fourth Labs

Only one parameter, can afford Brute Force search

\hat{y}=\sum_{i=1}^n x_i \geq b
y^=∑i=1nxi≥b\hat{y}=\sum_{i=1}^n x_i \geq b
Launch (within 6 months) 0 1 1 0 0 1 0 1 1 0
Weight (<160g) 1 0 1 0 0 0 1 0 0 1
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1 0
dual sim 1 1 0 0 0 1 0 1 0 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1 0
NFC 0 1 1 0 1 0 1 1 1 0
Radio 1 0 0 1 1 1 0 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0 0
Price > 20k 0 1 1 0 0 0 1 1 1 0
Like?      (y) 1 0 1 0 1 1 0 1 0 0
predicted         1 1 1 1 1 1 1 1 1 1
loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2
\hat{y}
y^\hat{y}

Learning Algorithm

How do we train our model?

(c) One Fourth Labs

Only one parameter, can afford Brute Force search

\hat{y}=\sum_{i=1}^n x_i \geq b
y^=∑i=1nxi≥b\hat{y}=\sum_{i=1}^n x_i \geq b
Launch (within 6 months) 0 1 1 0 0 1 0 1 1 0
Weight (<160g) 1 0 1 0 0 0 1 0 0 1
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1 0
dual sim 1 1 0 0 0 1 0 1 0 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1 0
NFC 0 1 1 0 1 0 1 1 1 0
Radio 1 0 0 1 1 1 0 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0 0
Price > 20k 0 1 1 0 0 0 1 1 1 0
Like?      (y) 1 0 1 0 1 1 0 1 0 0
predicted         1 1 1 1 1 1 1 1 1 0
loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2
\hat{y}
y^\hat{y}

Learning Algorithm

How do we train our model?

(c) One Fourth Labs

Only one parameter, can afford Brute Force search

\hat{y}=\sum_{i=1}^n x_i \geq b
y^=∑i=1nxi≥b\hat{y}=\sum_{i=1}^n x_i \geq b
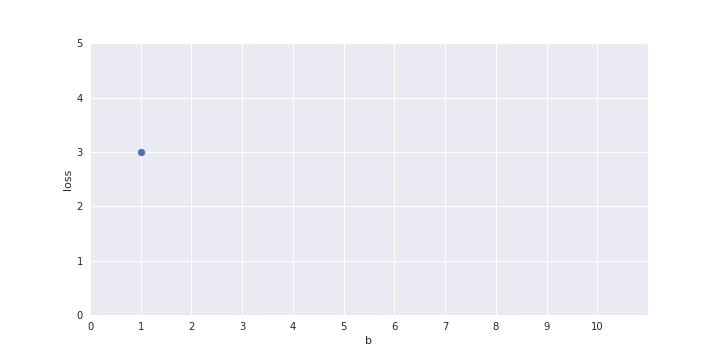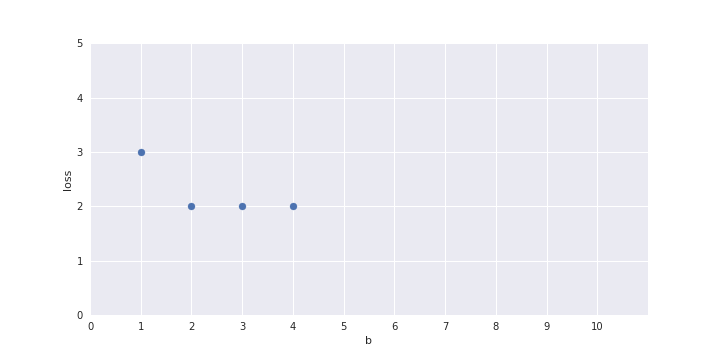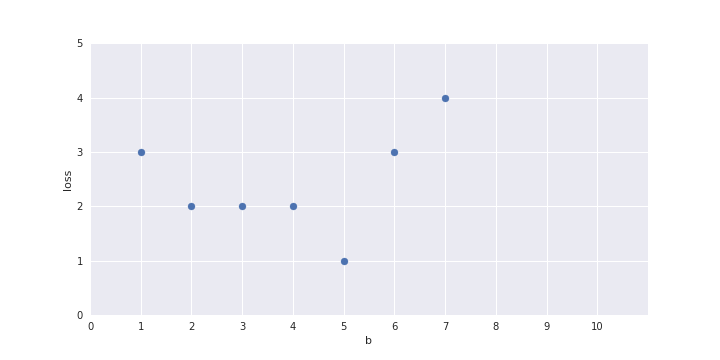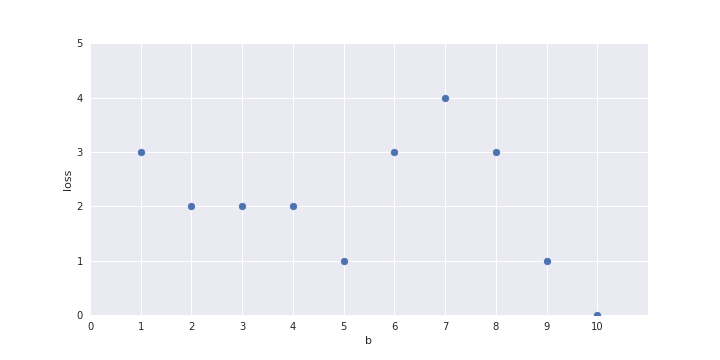
Launch (within 6 months) 0 1 1 0 0 1 0 1 1 0
Weight (<160g) 1 0 1 0 0 0 1 0 0 1
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1 0
dual sim 1 1 0 0 0 1 0 1 0 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1 0
NFC 0 1 1 0 1 0 1 1 1 0
Radio 1 0 0 1 1 1 0 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0 0
Price > 20k 0 1 1 0 0 0 1 1 1 0
Like?      (y) 1 0 1 0 1 1 0 1 0 0
predicted         1 0 0 1 1 1 1 0 0 0
\hat{y}
y^\hat{y}
loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2

Loss Function, Learning Algo

How do we train our model?

(c) One Fourth Labs

Demonstrate brute force search with a plot that varies \theta and plots loss function

 

* I think this slide will not be needed as we should be able to fit everything on the previous slide

Evaluation

How does MP perform?

(c) One Fourth Labs

Same train matrix from before (you can compress it -its ok even if it is not fully visible

 

Animation: (the parts in red will already be seen on the slide

- Show new test matrix below (with 4 rows)

- Show accuracy formula

- Go over each row and compute the model output. Show tick or cross in the space shown on RHS

- SHow the final accuracy number

Same model equations here with the value of b as learned from before

tick or cross here

some test matrix here

\text{Accuracy} = \frac{\text{Number of correctly classified data points}}{\text{Total number of data points}}
Accuracy=Number of correctly classified data pointsTotal number of data points\text{Accuracy} = \frac{\text{Number of correctly classified data points}}{\text{Total number of data points}}

Evaluation

How does MP perform?

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1 0
Weight (<160g) 1 0 1 0 0 0 1 0 0 1
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1 0
dual sim 1 1 0 0 0 1 0 1 0 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1 0
NFC 0 1 1 0 1 0 1 1 1 0
Radio 1 0 0 1 1 1 0 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0 0
Price > 20k 0 1 1 0 0 0 1 1 1 0
Like?      (y) 1 0 1 0 1 1 0 1 0 0
predicted         1 0 0 1 1 1 1 0 0 0
\text{Accuracy} = \frac{\text{Number of correctly classified data points}}{\text{Total number of data points}}
Accuracy=Number of correctly classified data pointsTotal number of data points\text{Accuracy} = \frac{\text{Number of correctly classified data points}}{\text{Total number of data points}}
\hat{y}=\sum_{i=1}^n x_i \geq 5
y^=∑i=1nxi≥5\hat{y}=\sum_{i=1}^n x_i \geq 5
loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2
1 0 0 1
0 1 1 1
0 1 1 1
0 1 0 0
1 0 0 0
0 0 1 0
1 1 1 0
1 1 1 0
0 0 1 0
0 1 0 0
0 1 1 0

Evaluation

How does MP perform?

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1 0
Weight (<160g) 1 0 1 0 0 0 1 0 0 1
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1 0
dual sim 1 1 0 0 0 1 0 1 0 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1 0
NFC 0 1 1 0 1 0 1 1 1 0
Radio 1 0 0 1 1 1 0 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0 0
Price > 20k 0 1 1 0 0 0 1 1 1 0
Like?      (y) 1 0 1 0 1 1 0 1 0 0
predicted         1 0 0 1 1 1 1 0 0 0
\text{Accuracy} = \frac{\text{Number of correctly classified data points}}{\text{Total number of data points}}
Accuracy=Number of correctly classified data pointsTotal number of data points\text{Accuracy} = \frac{\text{Number of correctly classified data points}}{\text{Total number of data points}}
\hat{y}=\sum_{i=1}^n x_i \geq 5
y^=∑i=1nxi≥5\hat{y}=\sum_{i=1}^n x_i \geq 5
loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2
1 0 0 1
0 1 1 1
0 1 1 1
0 1 0 0
1 0 0 0
0 0 1 0
1 1 1 0
1 1 1 0
0 0 1 0
0 1 0 0
0 1 1 0

Evaluation

How does MP perform?

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1 0
Weight (<160g) 1 0 1 0 0 0 1 0 0 1
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1 0
dual sim 1 1 0 0 0 1 0 1 0 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1 0
NFC 0 1 1 0 1 0 1 1 1 0
Radio 1 0 0 1 1 1 0 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0 0
Price > 20k 0 1 1 0 0 0 1 1 1 0
Like?      (y) 1 0 1 0 1 1 0 1 0 0
predicted         1 0 0 1 1 1 1 0 0 0
\text{Accuracy} = \frac{\text{Number of correctly classified data points}}{\text{Total number of data points}}
Accuracy=Number of correctly classified data pointsTotal number of data points\text{Accuracy} = \frac{\text{Number of correctly classified data points}}{\text{Total number of data points}}
\hat{y}=\sum_{i=1}^n x_i \geq 5
y^=∑i=1nxi≥5\hat{y}=\sum_{i=1}^n x_i \geq 5
loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2
1 0 0 1
0 1 1 1
0 1 1 1
0 1 0 0
1 0 0 0
0 0 1 0
1 1 1 0
1 1 1 0
0 0 1 0
0 1 0 0
0 1 1 0

Evaluation

How does MP perform?

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1 0
Weight (<160g) 1 0 1 0 0 0 1 0 0 1
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1 0
dual sim 1 1 0 0 0 1 0 1 0 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1 0
NFC 0 1 1 0 1 0 1 1 1 0
Radio 1 0 0 1 1 1 0 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0 0
Price > 20k 0 1 1 0 0 0 1 1 1 0
Like?      (y) 1 0 1 0 1 1 0 1 0 0
predicted         1 0 0 1 1 1 1 0 0 0
\text{Accuracy} = \frac{\text{Number of correctly classified data points}}{\text{Total number of data points}}
Accuracy=Number of correctly classified data pointsTotal number of data points\text{Accuracy} = \frac{\text{Number of correctly classified data points}}{\text{Total number of data points}}
\hat{y}=\sum_{i=1}^n x_i \geq 5
y^=∑i=1nxi≥5\hat{y}=\sum_{i=1}^n x_i \geq 5
loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2
1 0 0 1
0 1 1 1
0 1 1 1
0 1 0 0
1 0 0 0
0 0 1 0
1 1 1 0
1 1 1 0
0 0 1 0
0 1 0 0
0 1 1 0

Evaluation

How does MP perform?

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1 0
Weight (<160g) 1 0 1 0 0 0 1 0 0 1
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1 0
dual sim 1 1 0 0 0 1 0 1 0 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1 0
NFC 0 1 1 0 1 0 1 1 1 0
Radio 1 0 0 1 1 1 0 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0 0
Price > 20k 0 1 1 0 0 0 1 1 1 0
Like?      (y) 1 0 1 0 1 1 0 1 0 0
predicted         1 0 0 1 1 1 1 0 0 0
\text{Accuracy} = \frac{\text{Number of correctly classified data points}}{\text{Total number of data points}}
Accuracy=Number of correctly classified data pointsTotal number of data points\text{Accuracy} = \frac{\text{Number of correctly classified data points}}{\text{Total number of data points}}
\hat{y}=\sum_{i=1}^n x_i \geq 5
y^=∑i=1nxi≥5\hat{y}=\sum_{i=1}^n x_i \geq 5
loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2
1 0 0 1
0 1 1 1
0 1 1 1
0 1 0 0
1 0 0 0
0 0 1 0
1 1 1 0
1 1 1 0
0 0 1 0
0 1 0 0
0 1 1 0

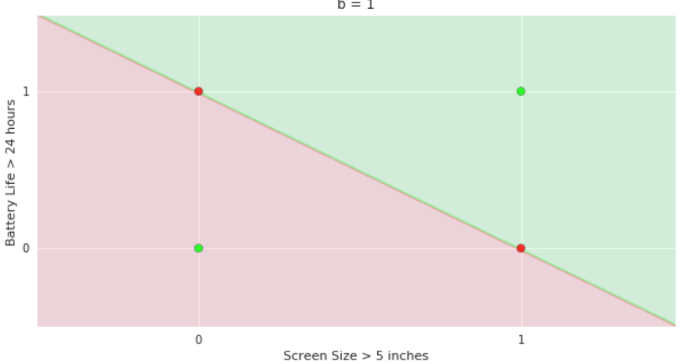
Geometric Interpretation

How to interpret the model of MP neuron gemoetrically?

(c) One Fourth Labs

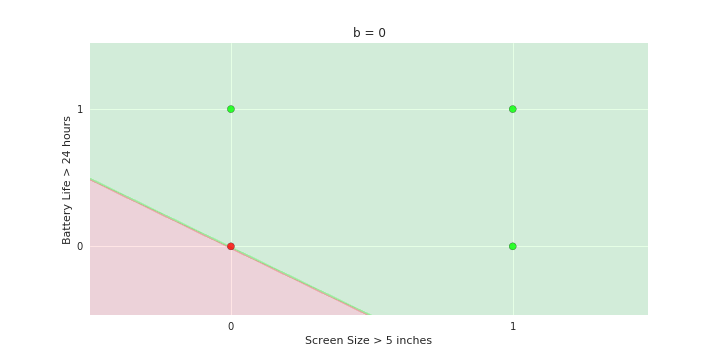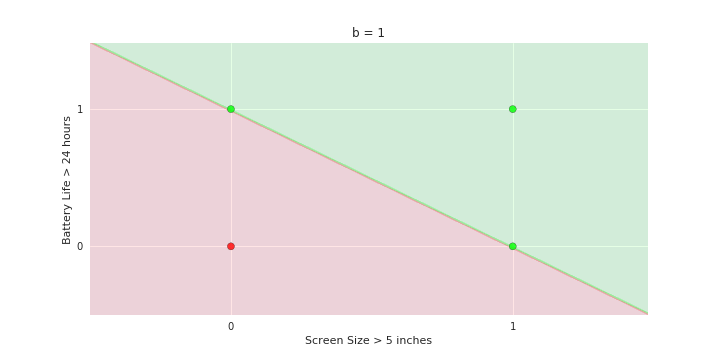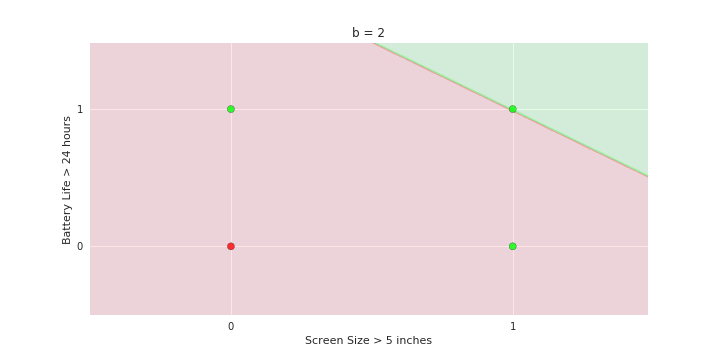
- We will now consider the phone like/no_like  problem again but with only two features: screen size > 5 in and battery life > 24 hours

 

- Show many phones but each of them can only belong to one of the 4 points {0,0} {0,1} {1,0} and {1,1}

 

- Now plot these points on the x1, x2 plane. There will be many points clustered at each of the 4 corners  0,0} {0,1} {1,0} and {1,1}

 

- Now show the model equations

Model equations here

- Now consider the line with be = 1

 

- Shade the area above this line as green and the area below this line as red

 

Now consider the line b = 0 and shade the area above this line as green and below as red

 

repeat for line b= 2

Geometric Interpretation

How to interpret the model of MP neuron gemoetrically?

(c) One Fourth Labs

Screen size (>5 in) 1 0 1 0 1 0 1 0 1 0
Battery (>24 hours) 0 0 0 1 0 1 0 1 0 0
Like 1 0 1 0 1 1 0 1 0 0
\hat{y}
y^\hat{y}
x_1
x1x_1
x_2
x2x_2
b
bb
\hat{y}=\sum_{i=1}^n x_i \gt 0
y^=∑i=1nxi&gt;0\hat{y}=\sum_{i=1}^n x_i \gt 0

Geometric Interpretation

How to interpret the model of MP neuron gemoetrically?

(c) One Fourth Labs

Screen size (>5 in) 1 0 1 1 1 0 1 0 1 0
Battery (>24 hours) 0 0 0 1 0 1 1 1 1 0
Like 1 0 1 0 1 1 0 1 0 0
\hat{y}
y^\hat{y}
x_1
x1x_1
x_2
x2x_2
b
bb
\hat{y}=\sum_{i=1}^n x_i \gt ?
y^=∑i=1nxi&gt;?\hat{y}=\sum_{i=1}^n x_i \gt ?

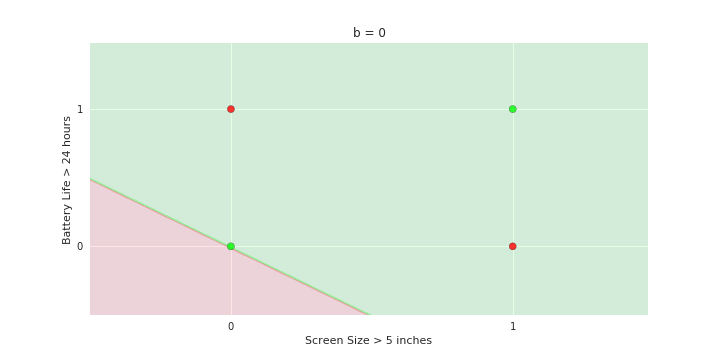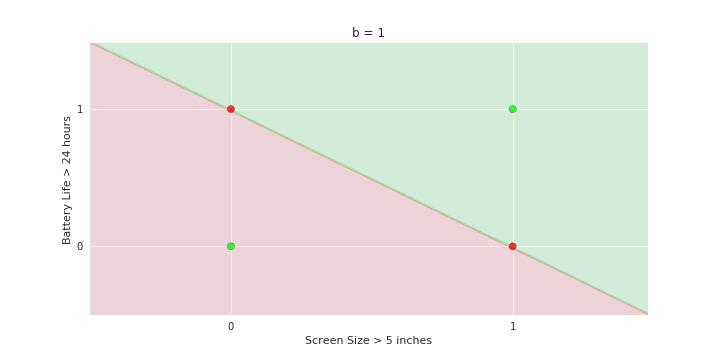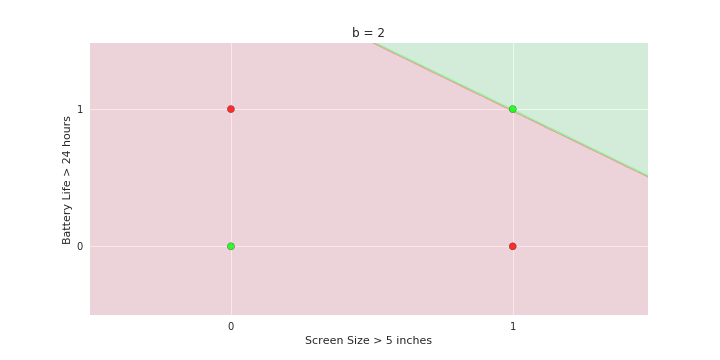
Linear

Fixed Slope

Few possible intercepts (b's)

Geometric Interpretation

Is this really a simple model ?

(c) One Fourth Labs

- Everything from the previous slide

 

- Now show what if the true data (i.e., all the points clustered around the 4 points

 {0,0} {0,1} {1,0} and {1,1} was actually like the XOR gate

 

- adjust the line by changing b=0. b1=1 and b=2 and show that there is no way you could have separated those points

 

Model equations here

Linear

Fixed Slope

Few possible intercepts (b's)

Take-aways

So will you use MP neuron?

(c) One Fourth Labs

Show the 6 jars at the top (again can be small)

 

\( \{0, 1\} \)

Boolean

show the line plot with XOR issue from the previous slide

show squared error loss

show search logo

show accuracy formula

Take-aways

So will you use MP neuron?

(c) One Fourth Labs

Show the 6 jars at the top (again can be small)

 

\( \{0, 1\} \)

Boolean

\text{Accuracy} = \frac{\text{Number of correctly classified data points}}{\text{Total number of data points}}
Accuracy=Number of correctly classified data pointsTotal number of data points\text{Accuracy} = \frac{\text{Number of correctly classified data points}}{\text{Total number of data points}}
loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2

Assignment

So will you use MP neuron?

(c) One Fourth Labs

Background of MP neuron

Understood model

Understood implications for data+task and loss function, learning algo

Understood the geometric interpretation to see that MP neuron cannot model complex relations

 

In the real world, data is not binary and relations are more complex

Hence this course continues

 

Will a binary search algorithm work?

Copy of Gokul's Copy of 1.5 McCulloch Pitts Neuron

By ananya_s_b

Source: Gokul Karthik

Copy of Gokul's Copy of 1.5 McCulloch Pitts Neuron

  • 470

More from ananya_s_b