PHC6194 SPATIAL EPIDEMIOLOGY

Spatial Data Types and Spatial Reference System
Hui Hu Ph.D.
Department of Epidemiology
College of Public Health and Health Professions & College of Medicine
January 22, 2020
Many-to-Many Relationships in SQL
Spatial Data Types and Spatial Reference System
Lab: PostGIS Part 1
Many-to-Many Relationships in SQL
Basic JOIN
1
2
3
C
A
B
INNER JOIN
=
2
3
A
B
1
2
3
C
A
B
LEFT JOIN
=
2
3
A
B
1
Basic JOIN
1
2
3
C
A
B
RIGHT JOIN
=
2
3
A
B
1
2
3
C
A
B
<<FULL>> JOIN
=
2
3
A
B
1
C
C
Theta JOIN
| Day |
|---|
| Jan 01 |
| Jan 02 |
| ... |
| Jan 30 |
| Jan 31 |
| Individual | Int_day |
|---|---|
| Ind 1 | Jan 10 |
| Ind 2 | Jan 11 |
| Ind 3 | Jan 12 |
JOIN
=
| Day | Individual |
|---|---|
| Jan 10 | Ind 1 |
| Jan 11 | Ind 1 |
| Jan 11 | Ind 2 |
| Jan 12 | Ind 1 |
| Jan 12 | Ind 2 |
| Jan 12 | Ind 3 |
| ... | ... |
| Jan 31 | Ind 1 |
| Jan 31 | Ind 2 |
| Jan 31 | Ind 3 |
ON Day>=Int_day
UNION
| Day |
|---|
| Jan 01 |
| Jan 02 |
| ... |
| Jan 30 |
| Jan 31 |
| Day |
|---|
| Feb 1 |
| Feb 2 |
| Feb 3 |
| Jan 01 |
UNION
=
| Day |
|---|
| Jan 1 |
| Jan 2 |
| Jan 3 |
| ... |
| Jan 31 |
| Feb 1 |
| Feb 2 |
| Feb 3 |
UNION ALL
| Day |
|---|
| Jan 01 |
| Jan 02 |
| ... |
| Jan 30 |
| Jan 31 |
| Day |
|---|
| Feb 1 |
| Feb 2 |
| Feb 3 |
| Jan 01 |
UNION ALL
=
| Day |
|---|
| Jan 1 |
| Jan 2 |
| Jan 3 |
| ... |
| Jan 31 |
| Feb 1 |
| Feb 2 |
| Feb 3 |
| Jan 01 |
Spatial Data Types and Spatial Reference System
Spatial Data Types
- Geometry:
- the planar type
- the very first model and still the most popular type
- the foundation of the other types
- uses the Cartesian math
- Geography:
- the spheroidal geodetic type
- lines and ploygons drawn on the earth's curved surface
- Raster:
- the multiband cell type
- space as a grid of rectangular cells, each containing a numeric array of values
- Topology:
- the relational model type
- models the world as a network of connected nodes, edges, and faces
- network
- These four types can coexist in the same database:
- e.g. you can have a geometry that defines the boundaries of a plant, and a raster that defines the concentration of toxic waste along each part of the boundary
Geometry Type
We can represent all geographical entities in 2D using 3 building blocks:
Point
Line
Polygon
- Simplified models of reality, and will never perfectly mimic the real thing
- Geometry type treats the world as a flat Cartesian grid
Geography Type
Similar to geometry, but account for the curvature of the earth
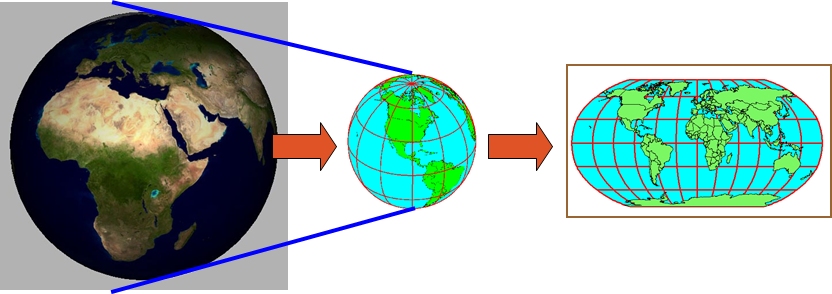
Shape of the earth
- Surface: The Earth's real surface
- Ellipsoid: Ideal, smooth surface
- Geoid: Bumpy surface, where gravity is equal for all locations
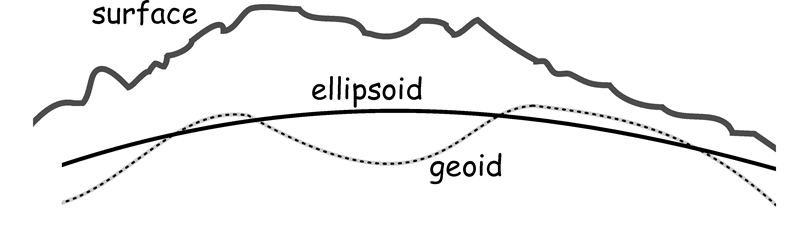
Shape of the earth (cont'd)

- Gauss determined in the early 19th century that the surface of the earth can be defined using gravitational measurements
- geoid: where gravity is equal for all locations
-
Geoid is far from spherical
- the core of the earth is not homogenous
- mass is distributed unevenly
- Geoid is the foundation of both planar and
geodetic models
Raster Type
Vector Model
- points, lines, polygons
- geometry and geography type

Raster Model
- exhaustive regular or irregular partitioning of space
Points
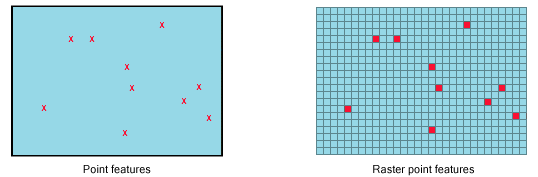
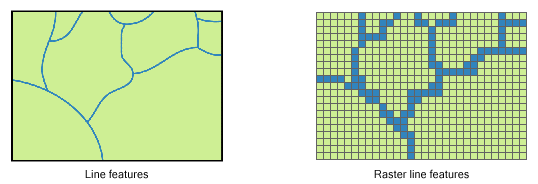
Lines
Topology Type
- Network of points, lines, and polygons
- Not concerned with the exact shape and location of geographic features, but with how they're connected to each other
- Useful in many applications:
- parcel (land lot) data, to ensure that the change of one parcel boundary adjusts all other parcels that share that boundary change as well
- road management, water boundaries, etc.
- architecture
Spatial Reference System
- SRS is the production of geodetics and cartography
- geodetics: the science of measuring and modeling the earth
- cartography: the science of representing the earth on flat maps
- Why do we need SRS?
- to bring in data from multiple sources and be able to overlay one atop another
- Many standards of SRS:
- most common one is the European Petroleum Survey Group (EPSG) numbering system
- take any two sources of data with the same EPSG number, and they will overlay perfectly
SRID
- Spatial Reference IDentifier
- It defines all the parameters of our data’s geographic coordinate system and projection.
- An SRID is convenient because it packs all the information about a map projection (which can be quite complex) into a single number.
-
http://spatialreference.org/ref/epsg/4326/
-
EPSG is a very recent SRS numbering system
- If you are using data from a few decades ago, you won't find EPSG number
-
The constituent pieces that form an SRS:
- ellipsoid
- datum
- projection
Ellipsoid

- Simplifications of the geoid which are generally good enough for most geographic modeling needs
- An ellipsoid is merely a 3D ellipse
- Instead of one ellipsoid to rule us all, people on different continents wanted their own ellipsoids to better reflect the regional curvature of the earth
- Today, the world is settling on the World Geodetic System (WGS 84) and Geodetic Reference System (GRS 80) ellipsoids
- WGS 84 is the standard of choice, and is what all GPS systems are based on
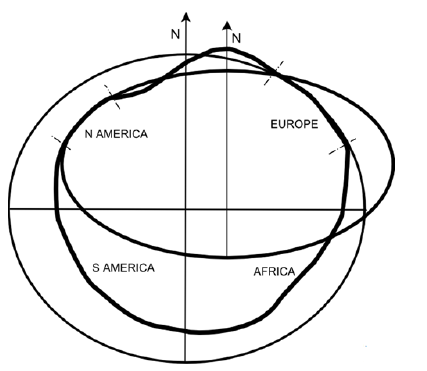
Common ellipsoids and their ellipsoidal parameters
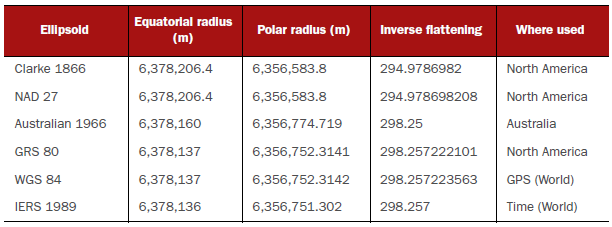
- Lon/lat with different ellipsoid are not the same
- they use different grounding points
- it's important to not just call things lon/lat: you can have NAD27 lon/lat, NAD80 lon/lat, etc. Each will be subtly different
Datum
- Ellipsoid only models the overall shape of the earth
- after picking out an ellipsoid, you need to anchor it to use it for real-world navigation
- even if two reference systems use the same ellipsoid, they can still have different anchors, or datum, on earth
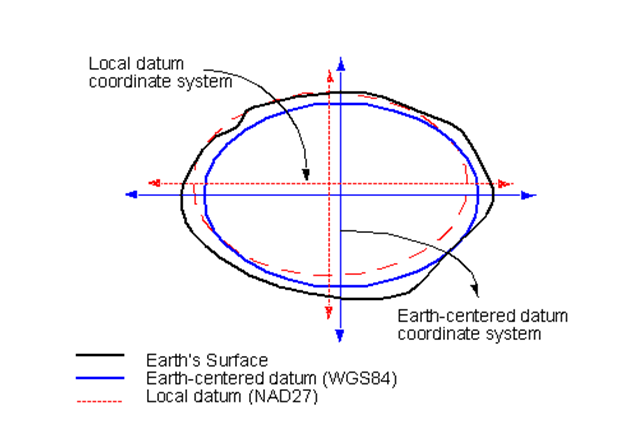
- Defines the position of the spheroid relative to the center of the earth.
- Global datum:
- uses the earth's center of mass as the origin
- Local datum:
- aligns its spheroid to closely fit the earth's surface in a particular area
- a point on the surface of the spheroid is matched to a particular position on the surface of the earth
- the coordinate system origin of a local datum is not at the center of the earth
Coordinate Reference System
- A coordinate reference system is only one necessary ingredient that goes into the making of an SRS and isn't SRS itself
- used to identify a point on your reference ellipsoid
- Most popular coordinate reference system for use is the geographical coordinate system
- also known as geodetic coordinate system or simply lon/lat
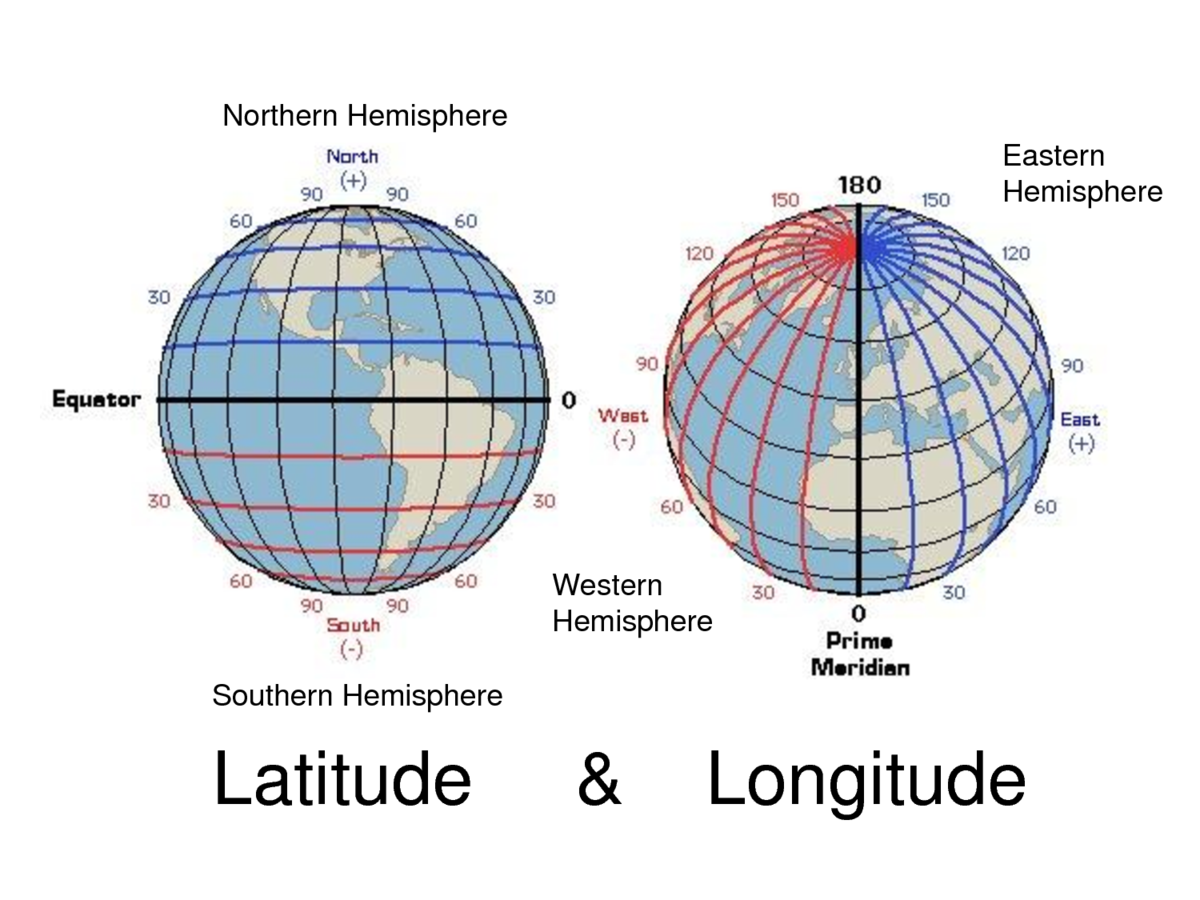
- Longitude and latitude
- Units: Degrees (DMS or DD)
Projection
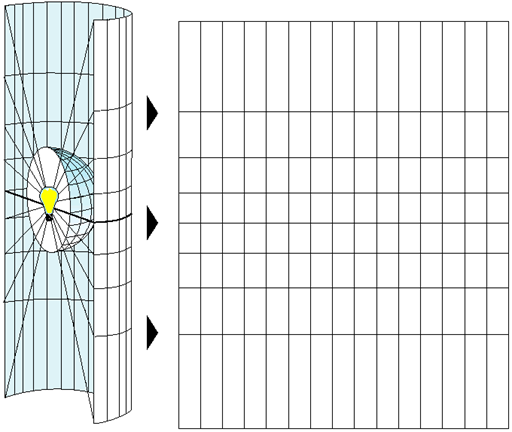
Taking an ellipsoidal earth and squashing it onto a flat surface
- Projection has distortion built in
- because geodetic and 3D globes are ellipsoidal, they by definition do not refer to a flat surface
- Why do we need to have 2D projections?
- the mathematical and visual simplicity that comes with planar (Euclidean) geometry
Distortion
- How exactly you squash an ellipsoidal earth on a flat surface depends on what you are trying to optimize for
- In creating a projection, we try to balance four conflicting features:
- measurement
- shape: how accurately does it represent angles
- direction: is north really north
- range of area supported
- E.g. if you want to span a large area, you have to either give up measurement accuracy or deal with the pain of maintaining multiple SRSs and some mechanisms to shift among them
Projection Types
Cylindrical projections
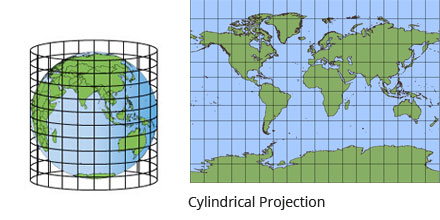
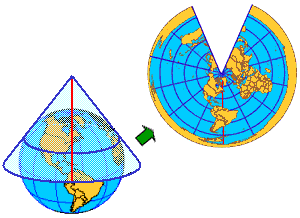
Conic projections
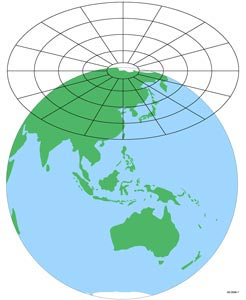
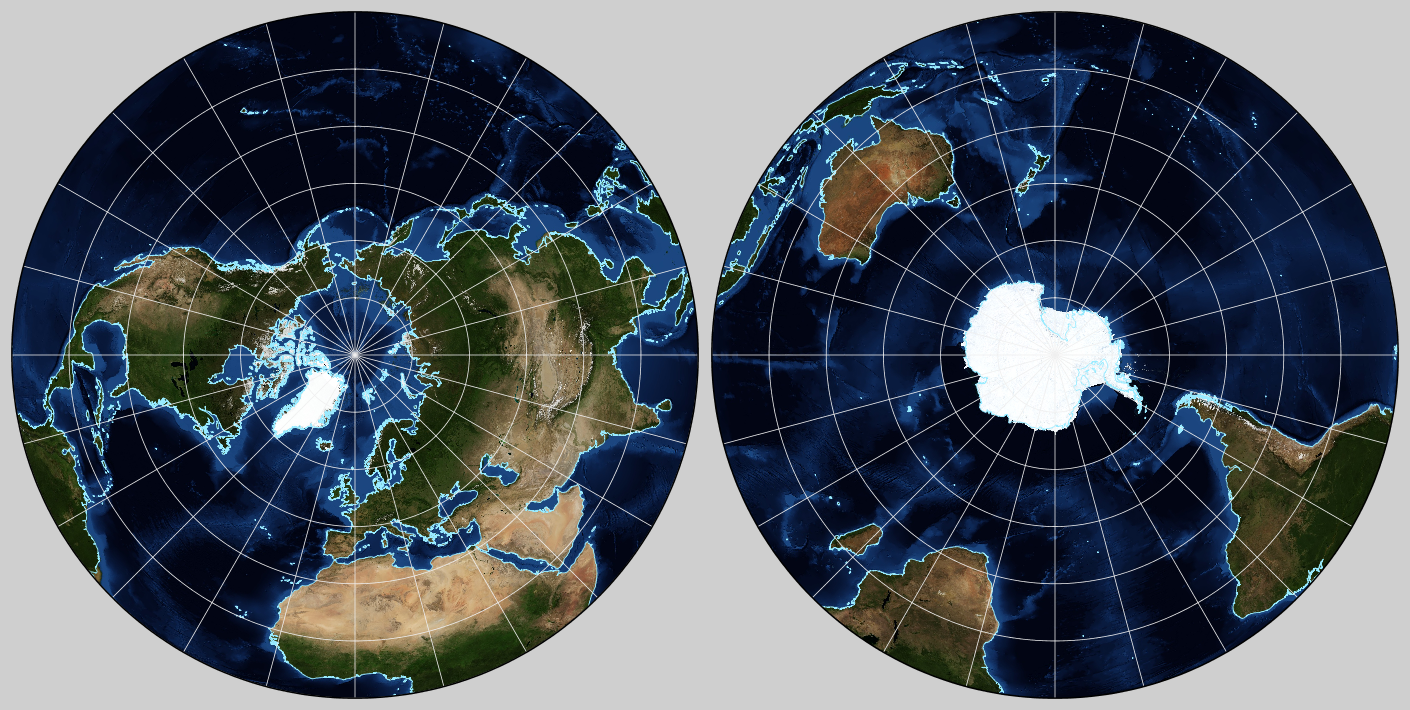
Azimuthal projections
Orientation of the paper roll around the globe
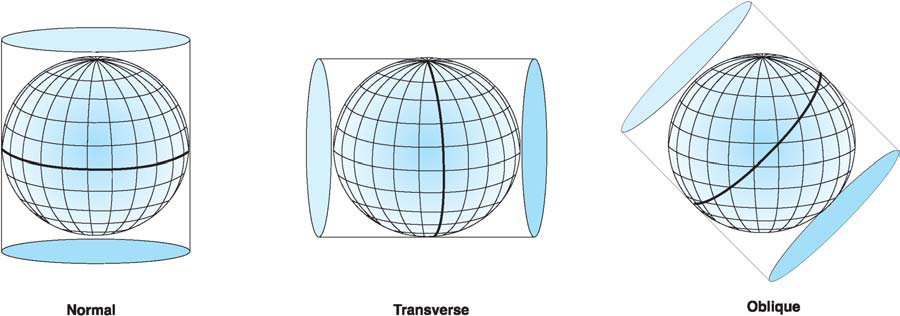
Main classes of planar coordinate systems
- Lambert Azimuthal Equal Area (LAEA)
- good for measurement and can cover large areas, but not great for shape
- US National Atlas (EPSG:2163)
- Lambert Conformal Conic (LCC)
- preserve shape more than area, good for measurement for the regions they serve, and distort poles
- best used for middle latitudes with east-west orientation
- Universal Trans Mercator (UTM)
- good for measurement, shape, and direction, but only span six-degree longitudinal strips, cannot be used for the polar regions
- Mercator
- good for preserve shape and direction, and spanning the globe, but not good for measurement
- common favorites for web map display since we only need to maintain one SRID
- National grid systems
- variant of UTM or LAEA, but are used to define a restricted region, such as a country
- State plane
- US spatial reference systems, usually designed for a specific state
- most are derived from UTM
Universal Transverse Mercator Coordinate System
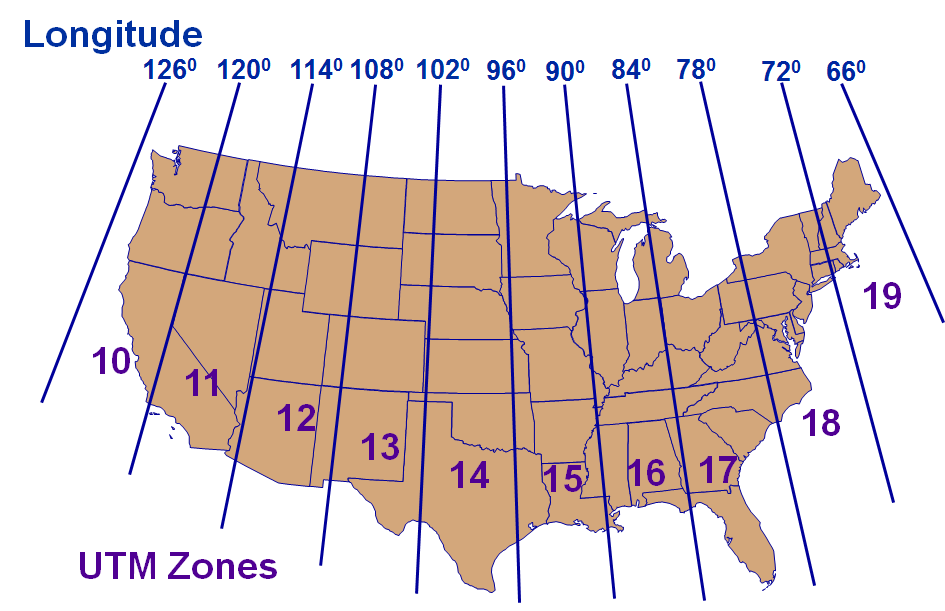
- World divided into 60 six-degree-wide zones
- From 80S to 84N
- Zones numbered 1-60 (N&S), W to E, starting at 180W
Differences between projections
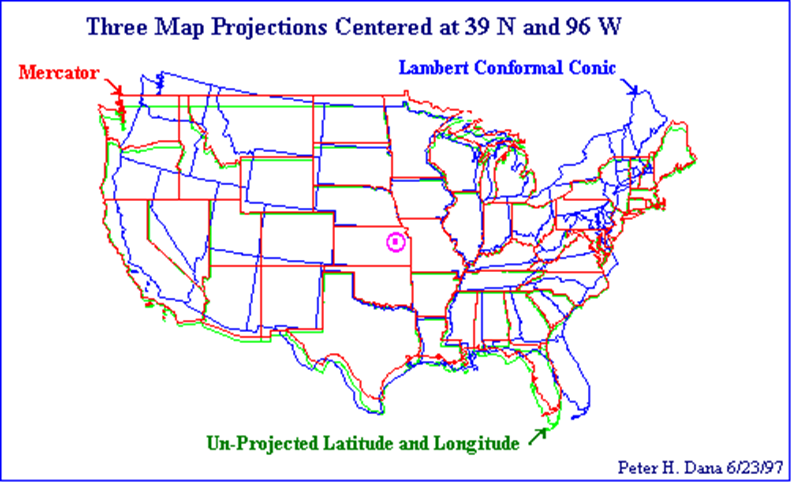
What spatial reference system is appropriate?
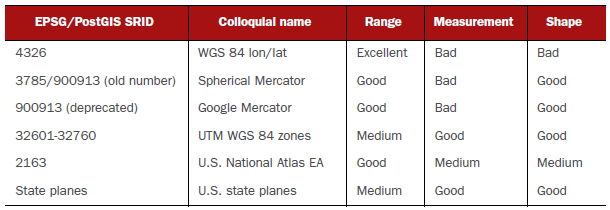
- Excellent: covers the globe
- Good: covers a large country like the US; the measurements for the area served are usually within a meter for length, area, and distance calculations
- Medium: covers several degrees or a large state; measurements are accurate within meters, but can be as much as 10 meters off
- Bad: measurements don't have useful units
Lab: PostGIS Part 1
git pull
Type Modifiers
geometry(POINT,4326)data type
subtype type modifier
SRID type modifier
Geometry: Points and Linestrings
POINT
POINTZ
POINTM
POINTZM
LINESTRING
LINESTRINGZ
LINESTRINGM
LINESTRINGZM- A point in 2D space specified by its X and Y coordinates
- A point in 3D space specified by its X, Y, and Z coordinates
- A point in 2D space with a measured value specified by its spatial X and Y coordinates plus an M value
- A point in 3D space with a measured value specified by its X, Y, and Z coordinates plus an M value
- A linestring in 2D specified by two or more distinct POINTs
- A linestring in 3D specified by two or more distinct POINTZs
- A linestring in 2D specified by two or more distinct POINTMs
- A linestring in 3D specified by two or more distinct POINTZMs
Geometry: Polygons
- Closed linestrings are the building block of polygons
- A polygon contains all the enclosed area, and its boundary is the linestring that forms it
- The enclosed linestring outlining the boundary of the polygon is called the ring of the polygon. More specifically, it's the exterior ring.
POLYGONCollection of Geometries
- A collection of geometries groups separate geometries that logically belong together:
- multipoints
- multilinestrings
- multipolygons
- geometrycollection
- can contain any kind of geometry as long as all geometries in the set have the same spatial reference system and the same coordinate dimensions
Geography
- In PostGIS, geography starts by assuming that all your data is based on a geodetic coordinate system, specifically the WGS 84 lon/lat SRID of 4326
- Only include support for basic subtypes of points, linestrings, and polygons, and no support for anything above 2D space
- The structure of the geography data mimic those of geometry
- everything you know about geometry applies to geography with no changes except for swapping out the term geometry for geography in both data type and function names
PHC6194-Spring2020-Lecture3
By Hui Hu
PHC6194-Spring2020-Lecture3
Slides for Lecture 3, Spring 2020, PHC6194 Spatial Epidemiology
- 1,046



