Generative Solutions for Cosmic Problems
florpi
https://florpi.github.io/
IAIFI Fellow
Carol(ina) Cuesta-Lazaro
1. Probabilistic debiasing of the cosmic web
2. Physical priors on EFT bias parameters
3. How would a Machine learn a "bias expansion"?
Outline
Inference a la gradient descent
Base Distribution
Target Distribution
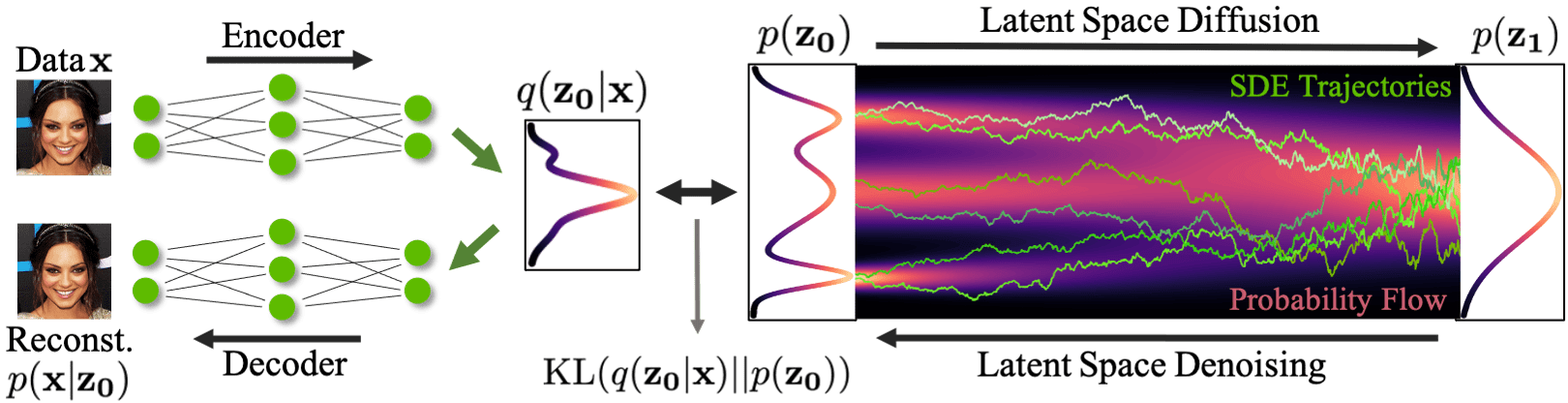
Bridging two distributions
z \sim p(z)
p(z)
x \sim p(x)
p(x)
\mathcal{L}_\phi = -\sum_i \log p_\phi(x_i)
Make the data as likely as possible
Prompt
A person half Yoda, half Gandalf
p_\phi(\rho_\mathrm{DM}|\rho_\mathrm{Galaxies})
1 to Many:
["Debiasing with Diffusion: Probabilistic reconstruction of Dark Matter fields from galaxies"
Ono et al arXiv:2403.10648]
Victoria Ono
Core Park
1. From Galaxies to Dark Matter
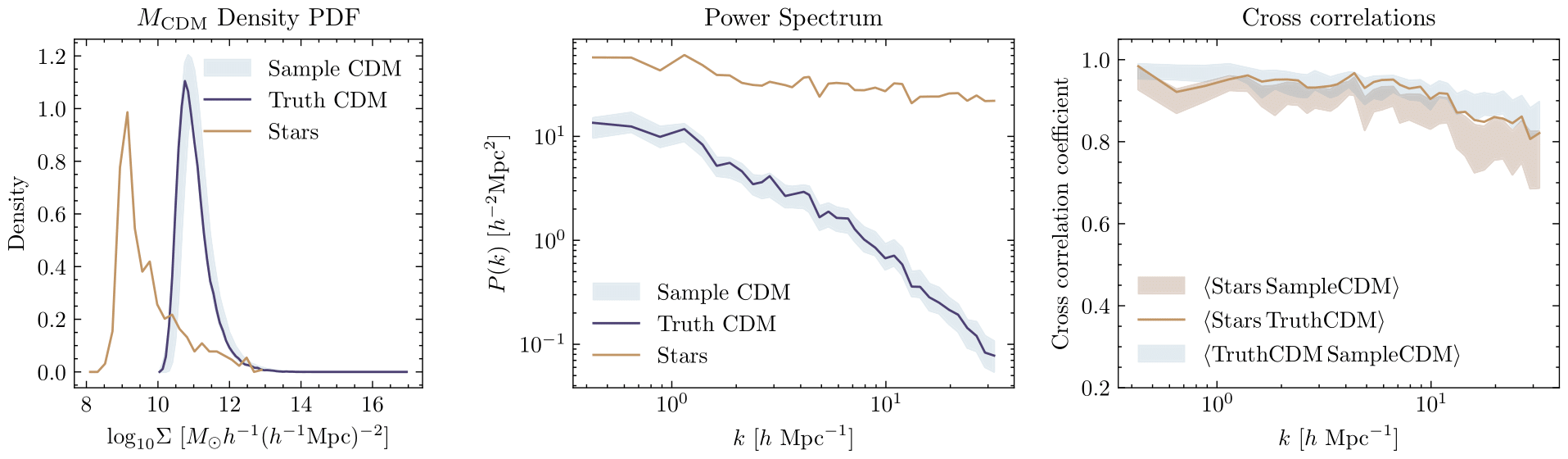
Truth
Sampled
Observed
Small
Large
Scale (k)
Power Spectrum
Small
Large
Scale (k)
Cross correlation
TNG-300
True DM
Inferred DM
Size of training simulation
Galaxy Cluster
Void
[arXiv:2403.10648]
Model trained on Astrid subgrid model
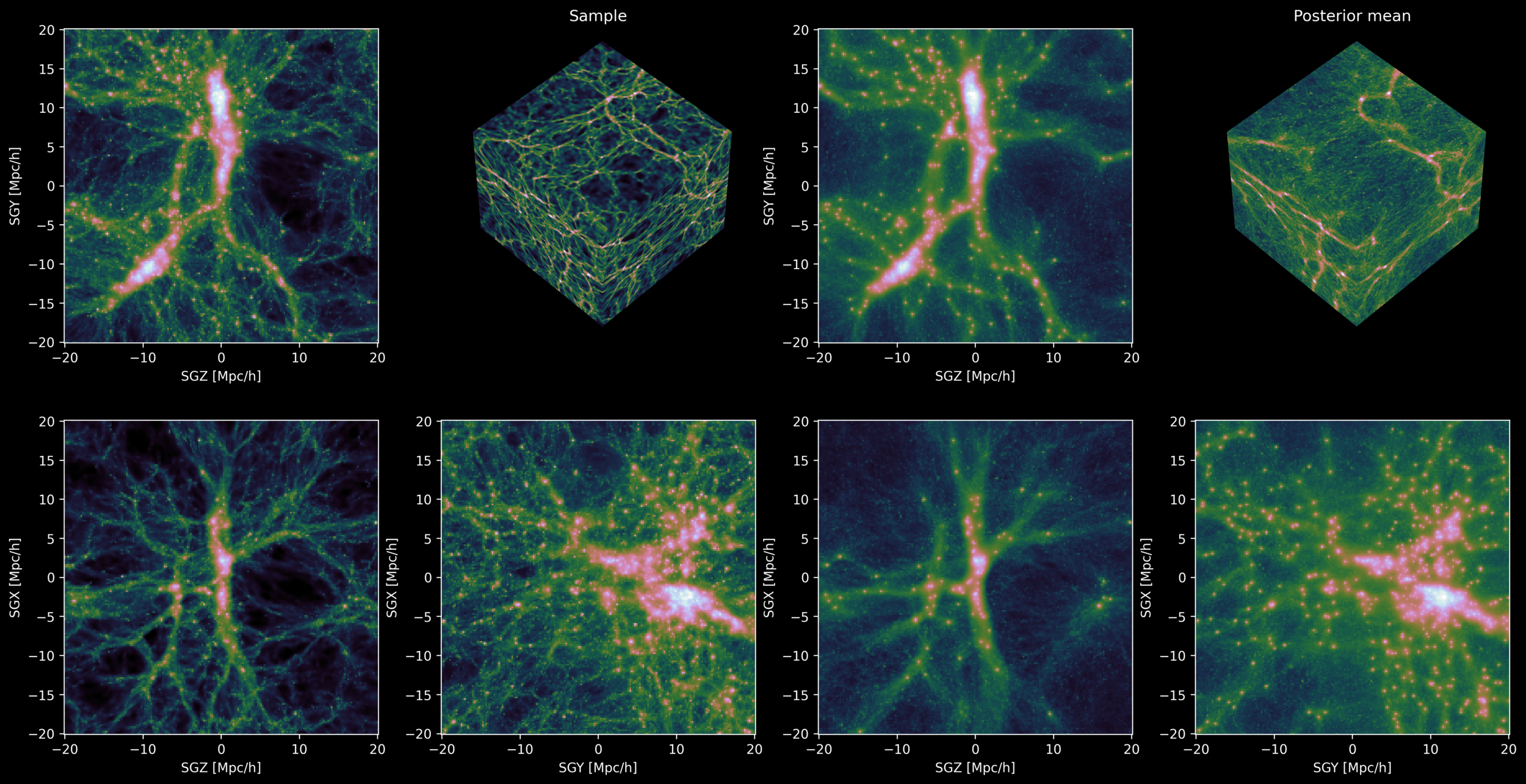
["3D Reconstruction of Dark Matter Fields with Diffusion Models: Towards Application to Galaxy Surveys" Park, Mudur, Cuesta-Lazaro et al (in-prep)]
Posterior Sample
Posterior Mean
Debiasing Cosmic Flows
[Video credit: Francisco Villaescusa-Navarro]
Gas density
Gas temperature
Subgrid model 1
Subgrid model 2
Subgrid model 3
Subgrid model 4
2. But, Simulations are nonsense?
Mikhail Ivanov
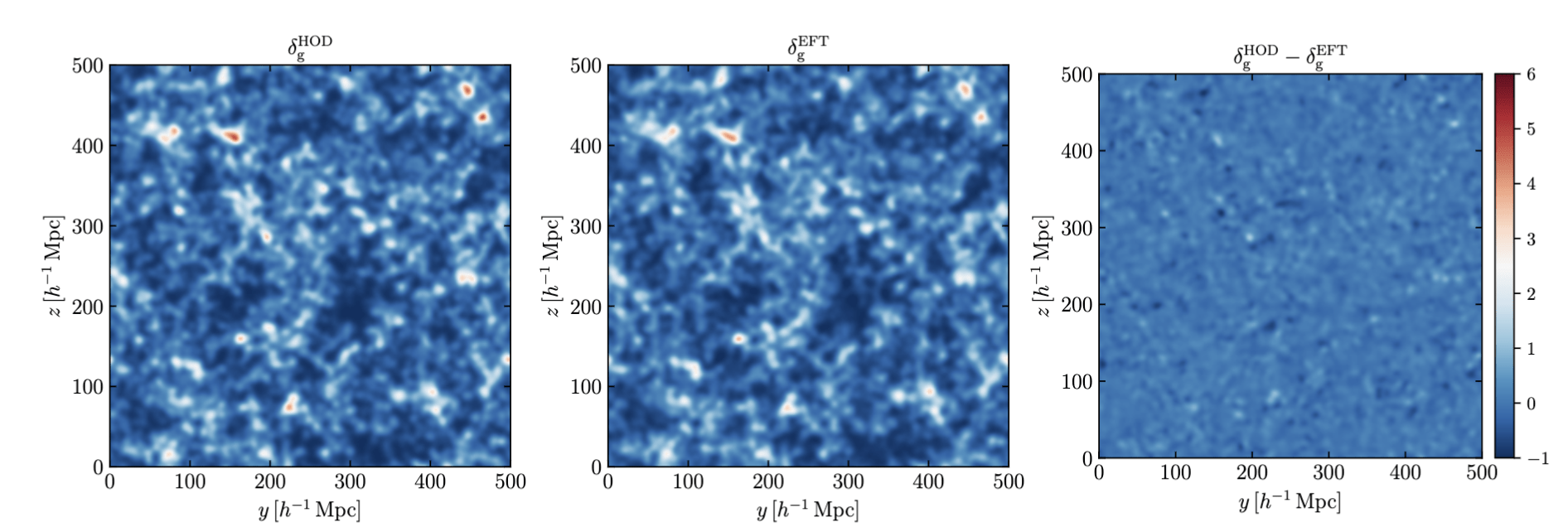
Robust galaxy bias model: Effective field Theories
+ Simulation as priors
p(b)
p(\mathrm{Galaxies}|b)
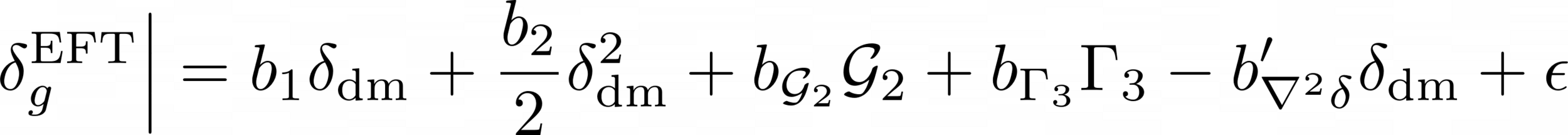
Field-level EFT
["Full-shape analysis with simulation-based priors: constraints on single field inflation from BOSS" Ivanov, Cuesta-Lazaro et al arXiv:2402.13310]
Andrej Obuljen
Michael Toomey
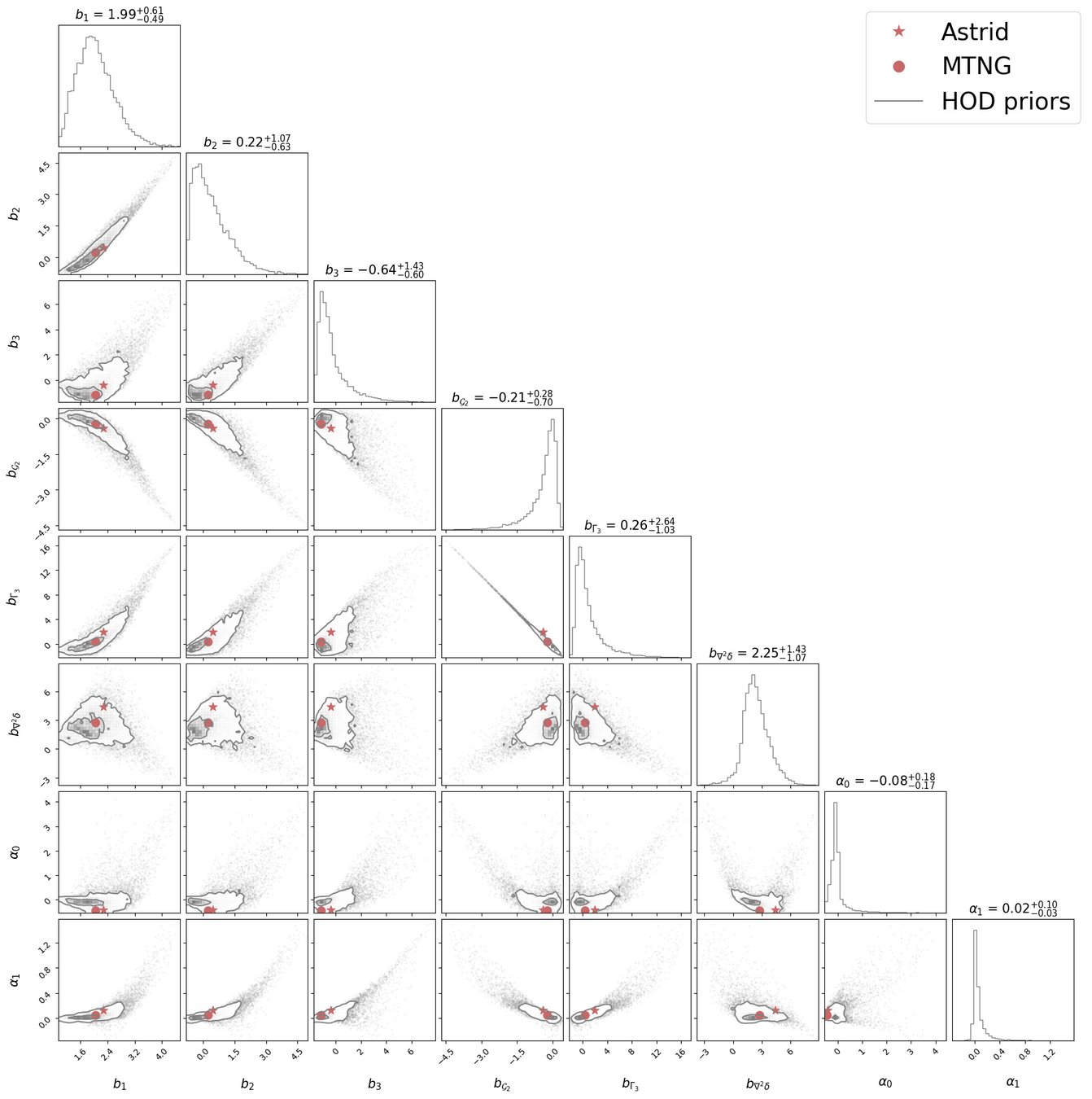
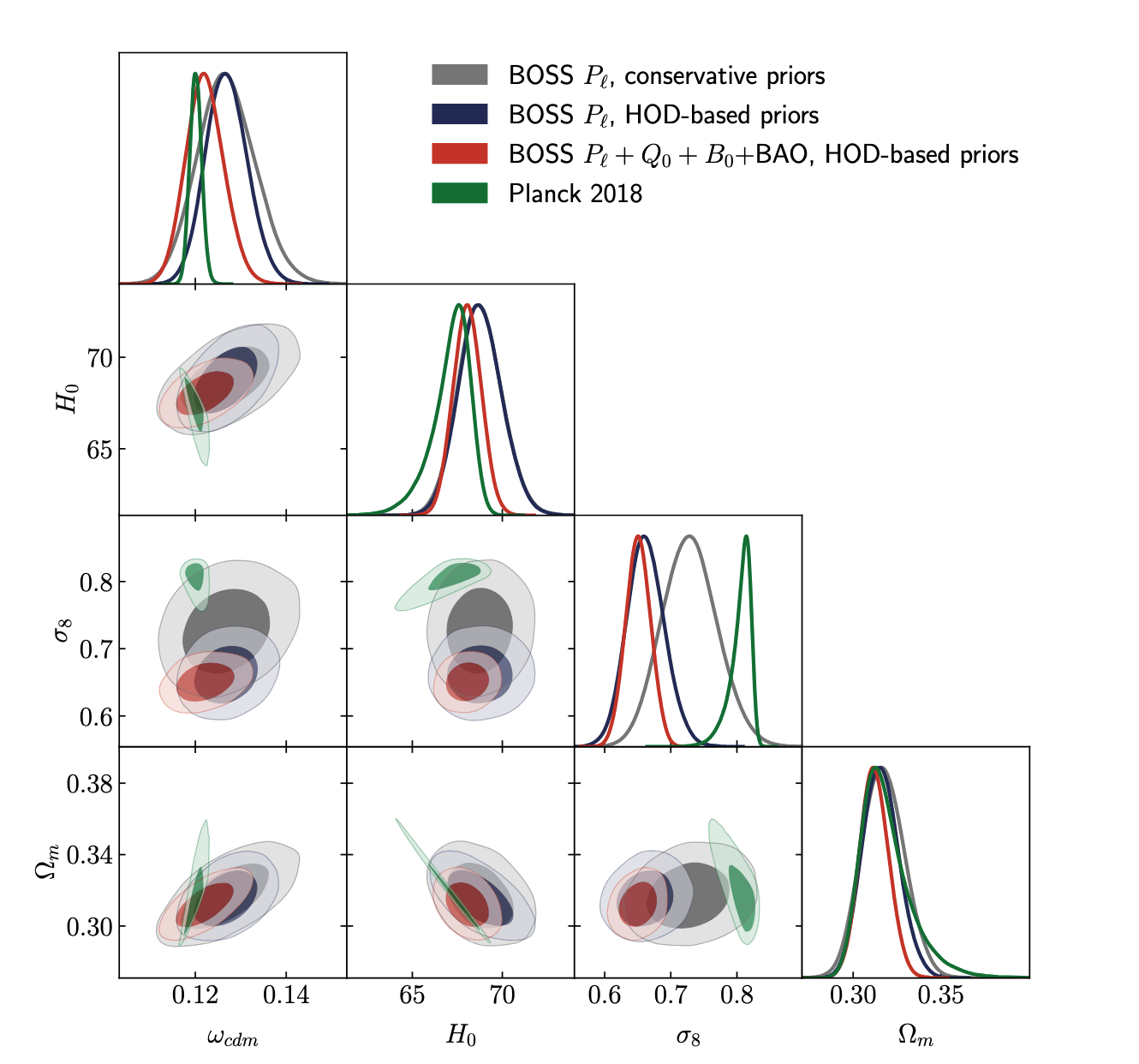
["Full-shape analysis with simulation-based priors: cosmological parameters and the structure growth anomaly" Ivanov, Obuljen, Cuesta-Lazaro, Toomey arXiv:2409.10609]
p(\mathrm{HOD}|b)
\Omega_m, \sigma_8
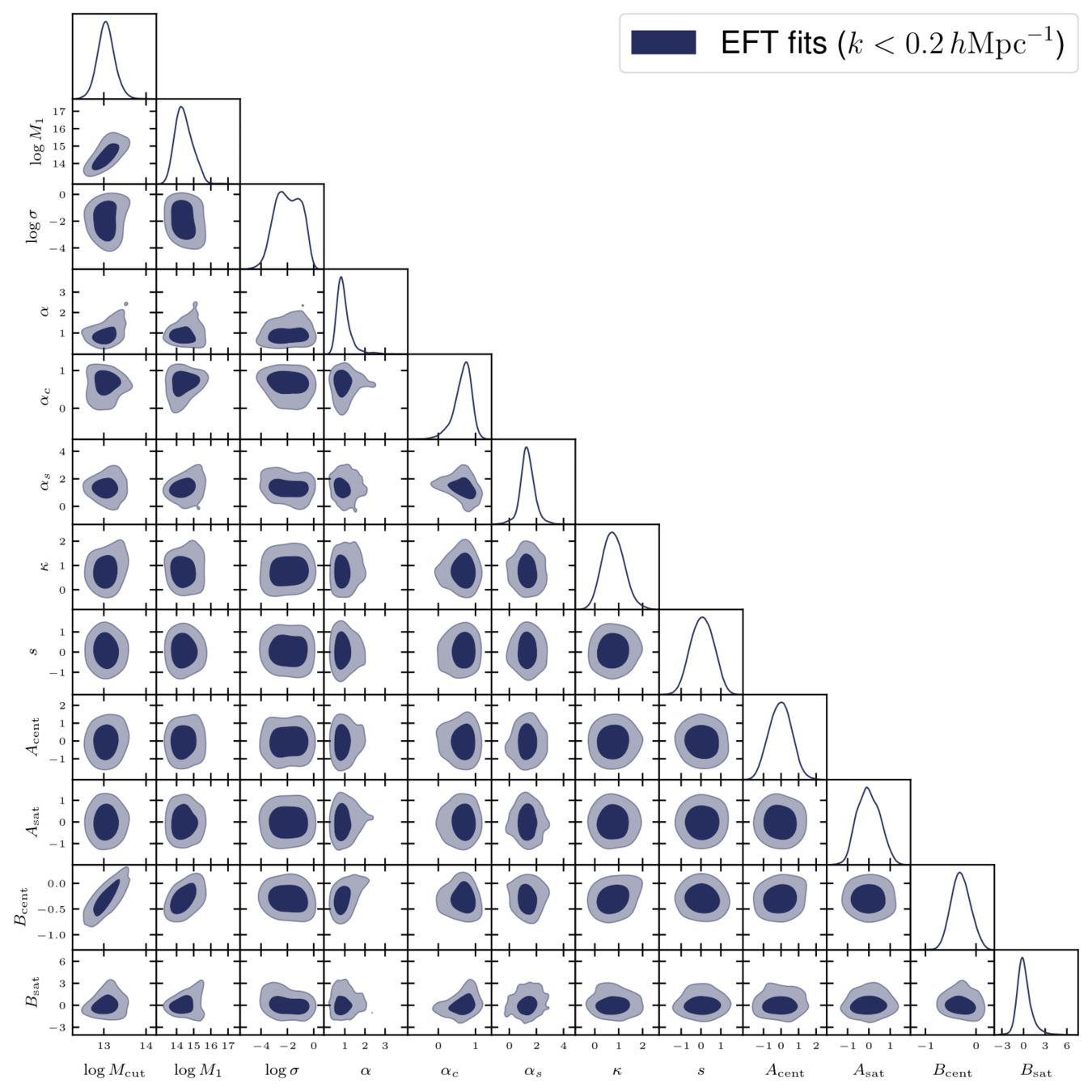
Simulator 1
Simulator 2
z
p(
, z)
Dark Matter
Feedback
\Omega_m, \sigma_8
i) Contrastive
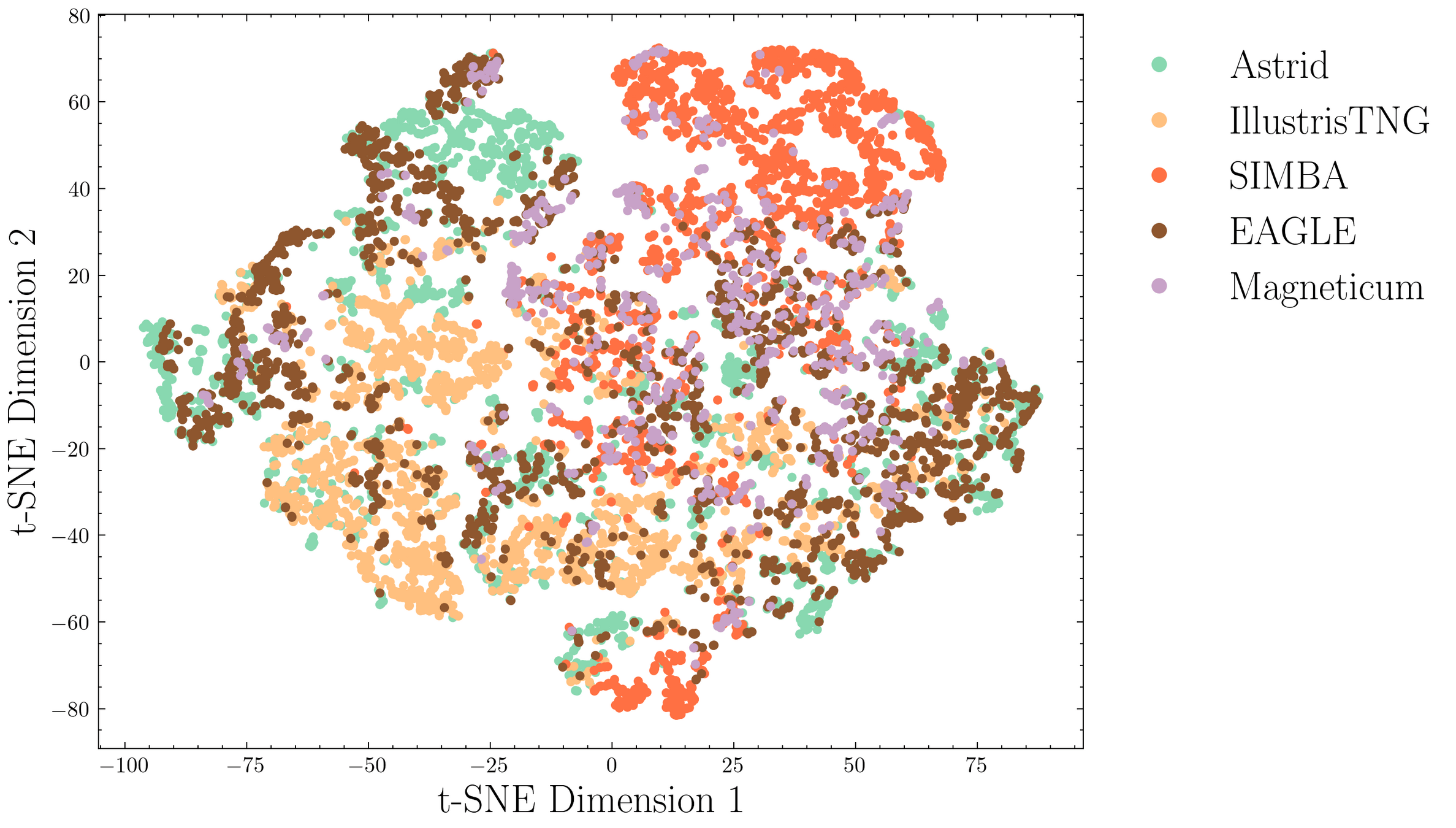
3. Learning the feedback manifold
Baryonic fields
ii) Generative
Baryonic fields
Dark Matter
Generative model
Total matter, gas temperature,
gas metalicity
p(
)
, z)
p(
z = f_\theta (
)
Encoder
+
p(\mathcal{C},z|
)
z
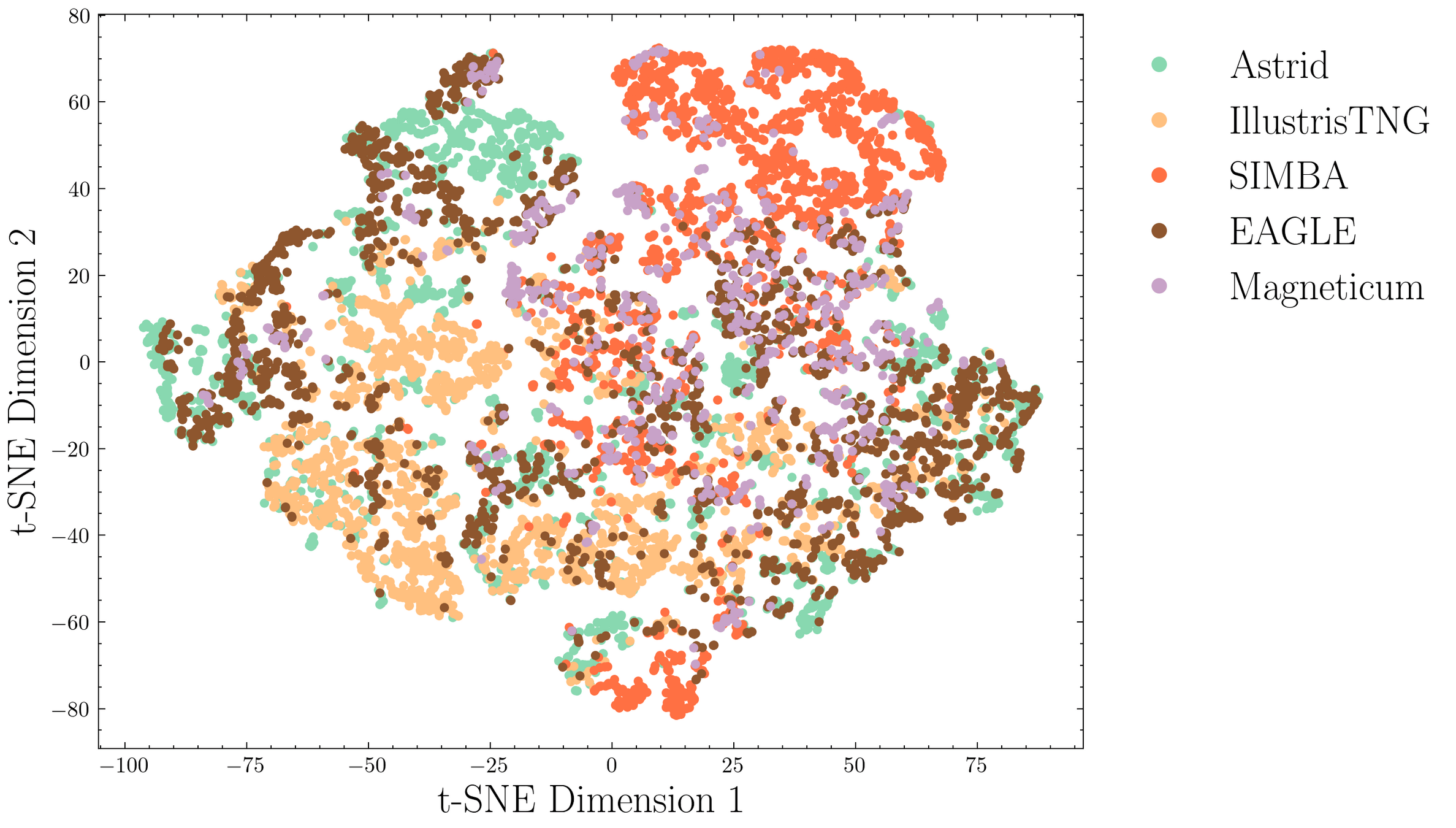
1. Probabilistic debiasing of the cosmic web
2. Physical priors on EFT bias parameters
3. How would a Machine learn a "bias expansion"?
Mock Barcelona
By carol cuesta
