Machine Learning solutions for Cosmic Problems
IAIFI Fellow, MIT / Center for Astrophysics
Carolina Cuesta-Lazaro
Symmetries, Feedback and Controllable simulations
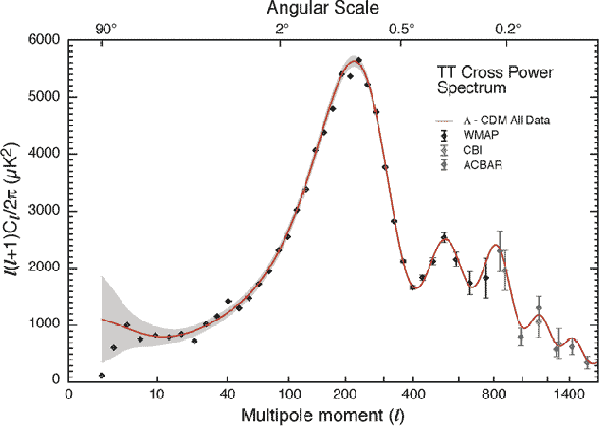
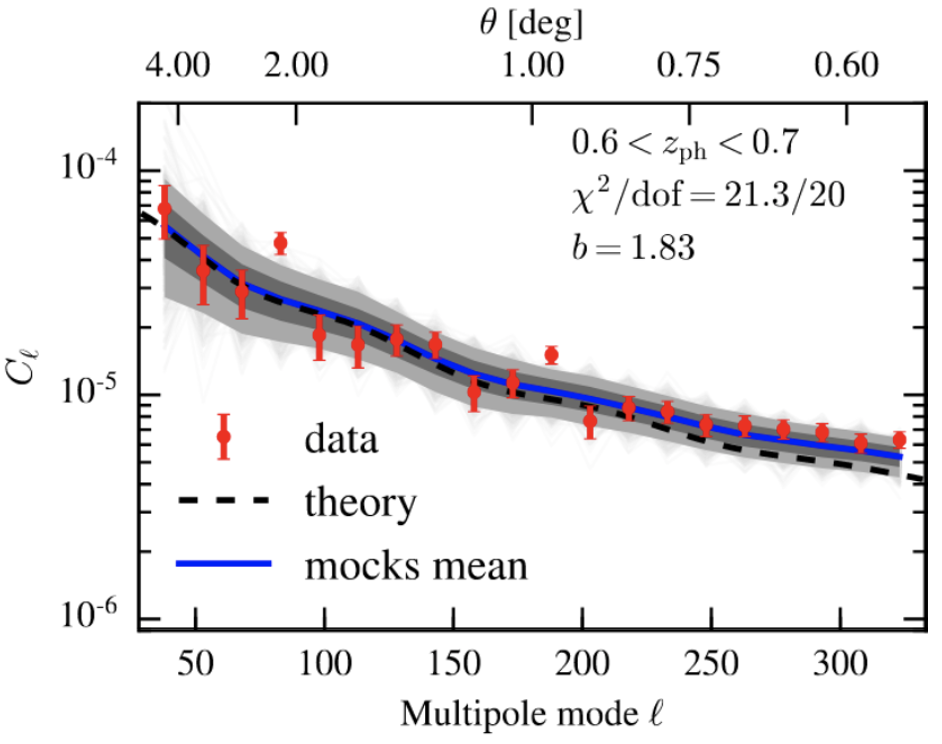
1-Dimensional
Machine Learning
Secondary anisotropies
Galaxy formation
Intrinsic alignments
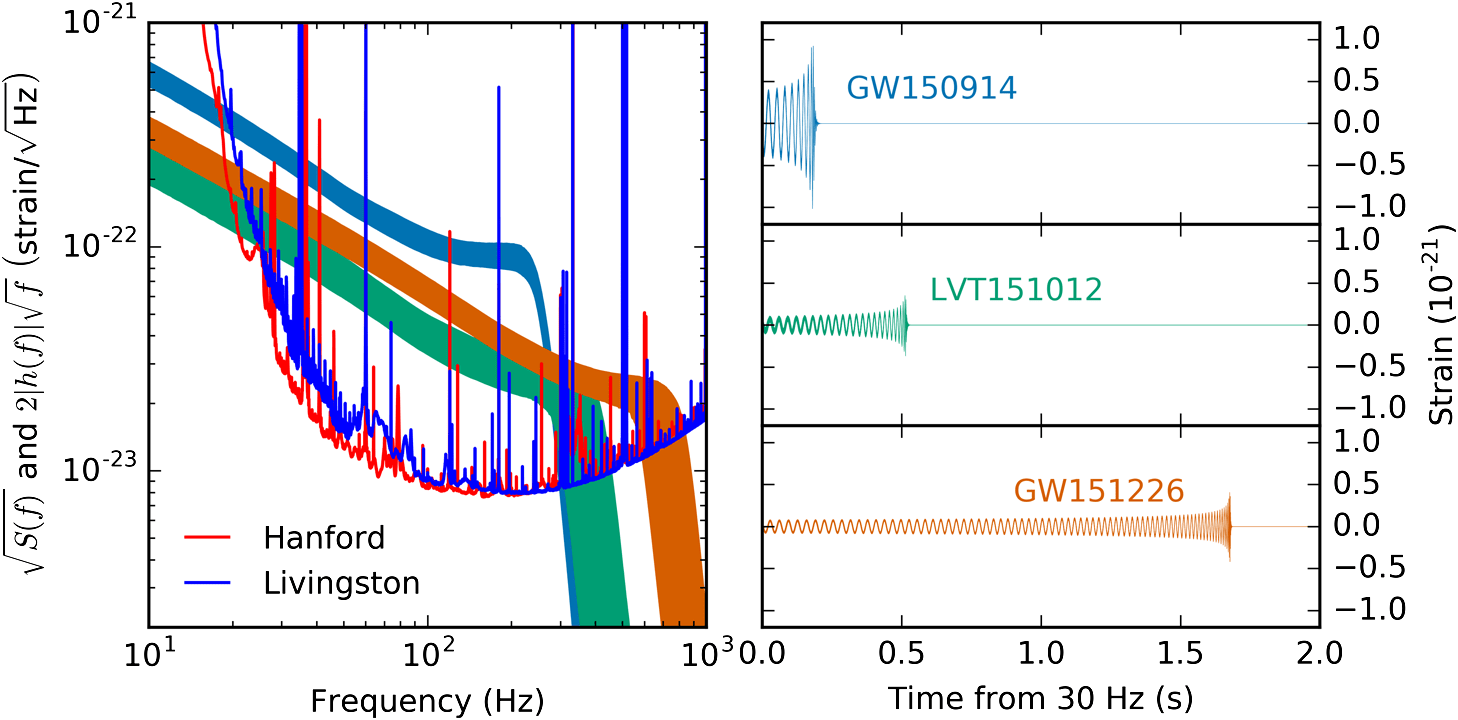
DESI, DESI-II, Spec-S5
Euclid / LSST
Simons Observatory
CMB-S4
Ligo
Einstein
The era of Big Data Cosmology
xAstrophysics
5-Dimensional
w_0, w_a, f\sigma_8, \Omega_m, \sum m_\nu
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
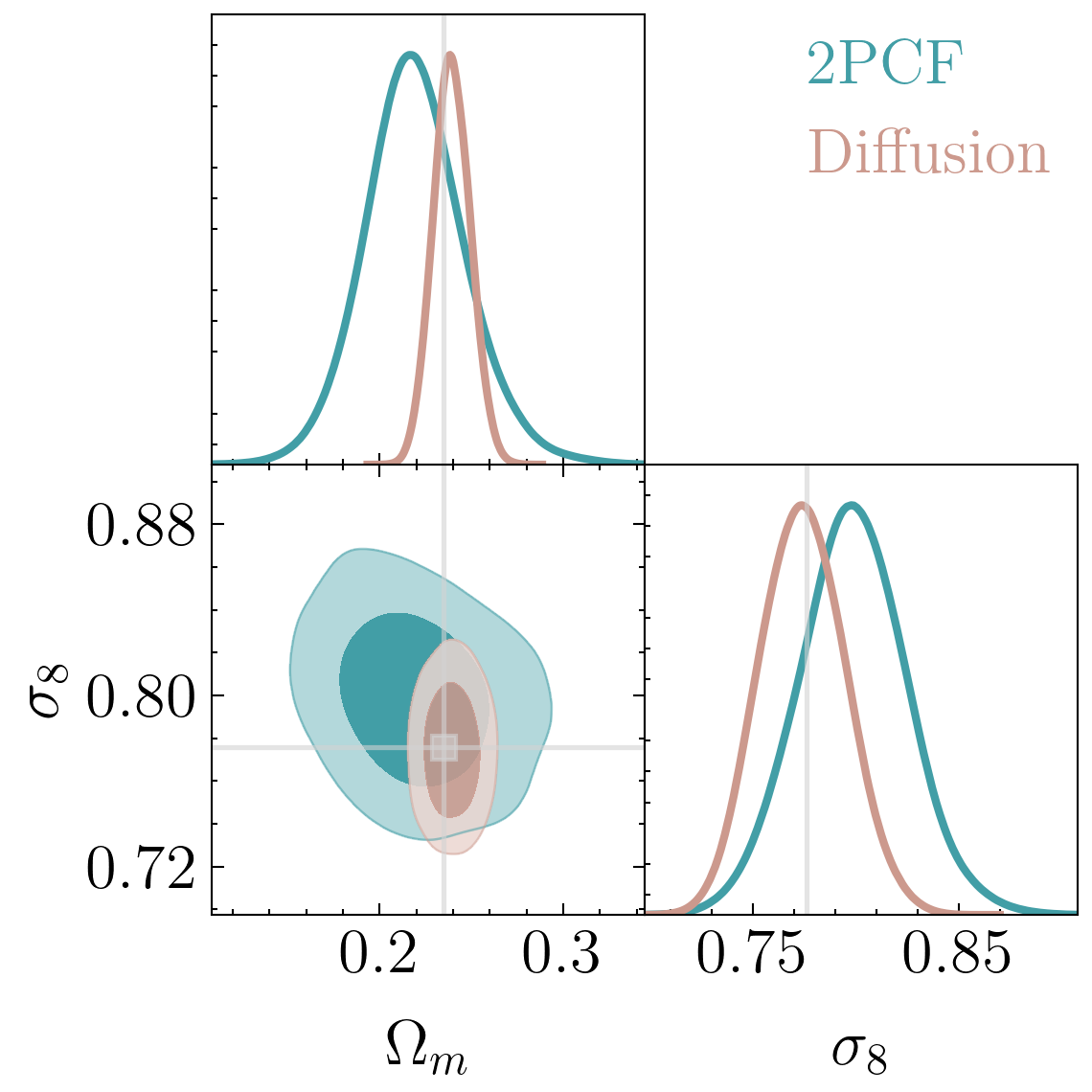
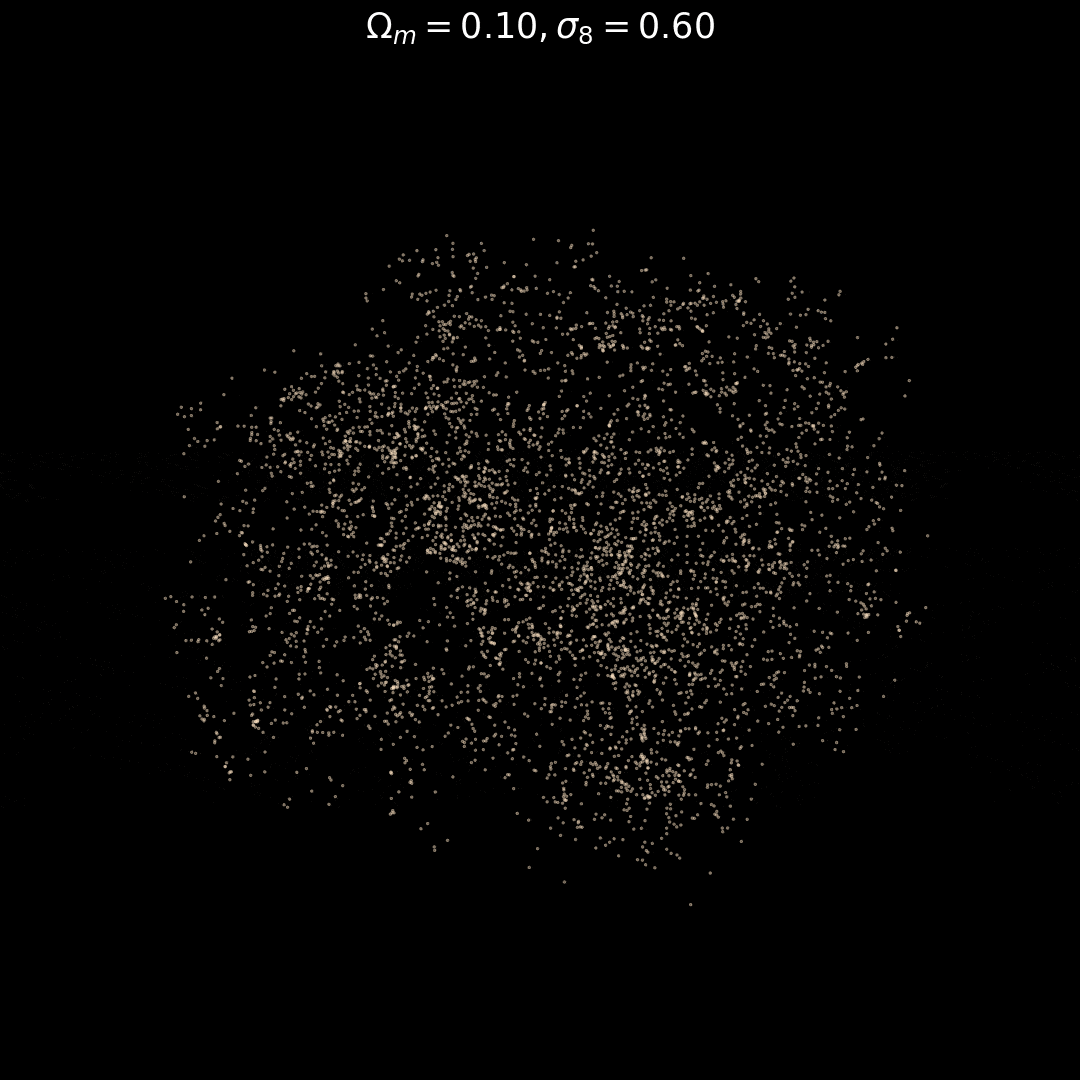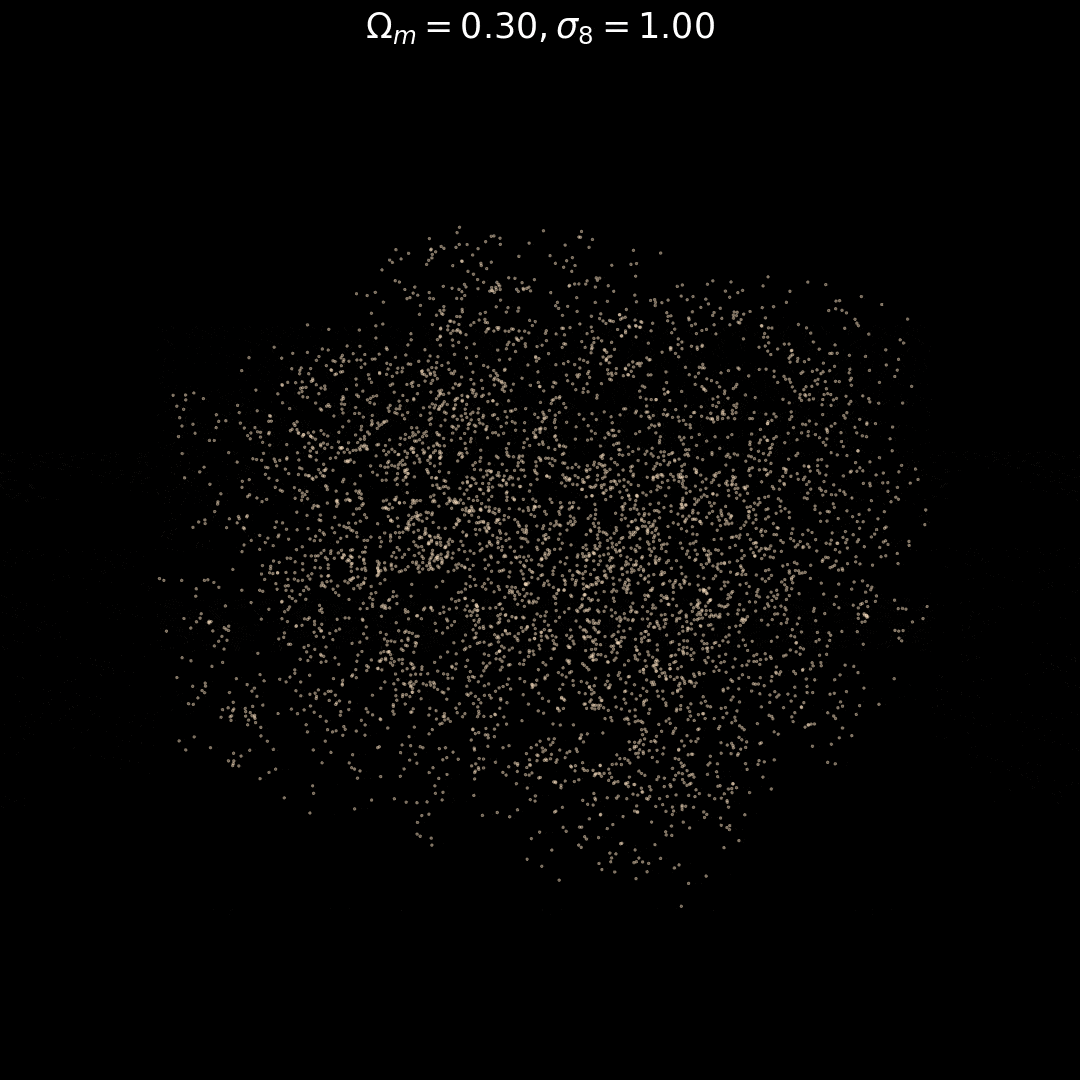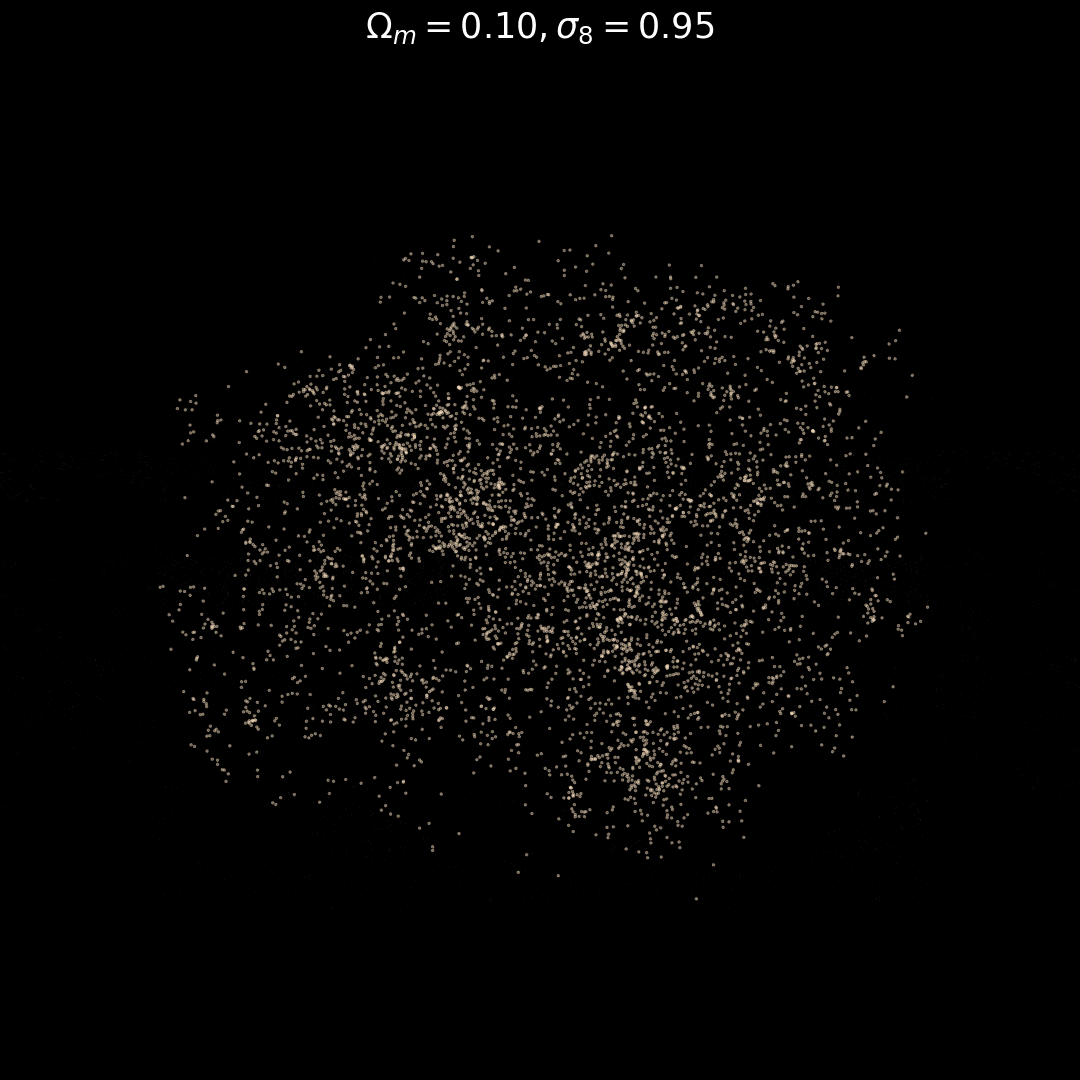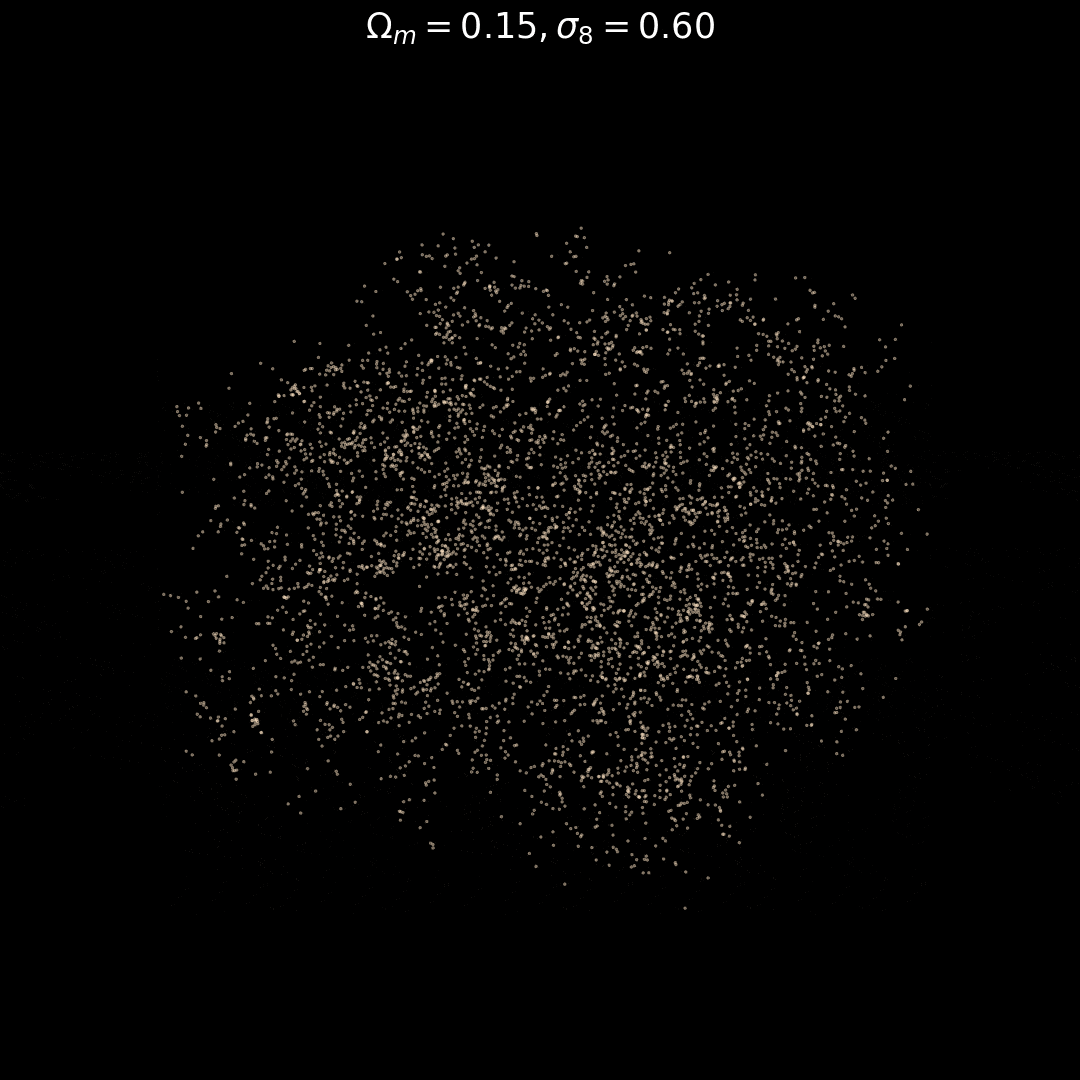
Generative models as Fast Emulators + Likelihood Estimators
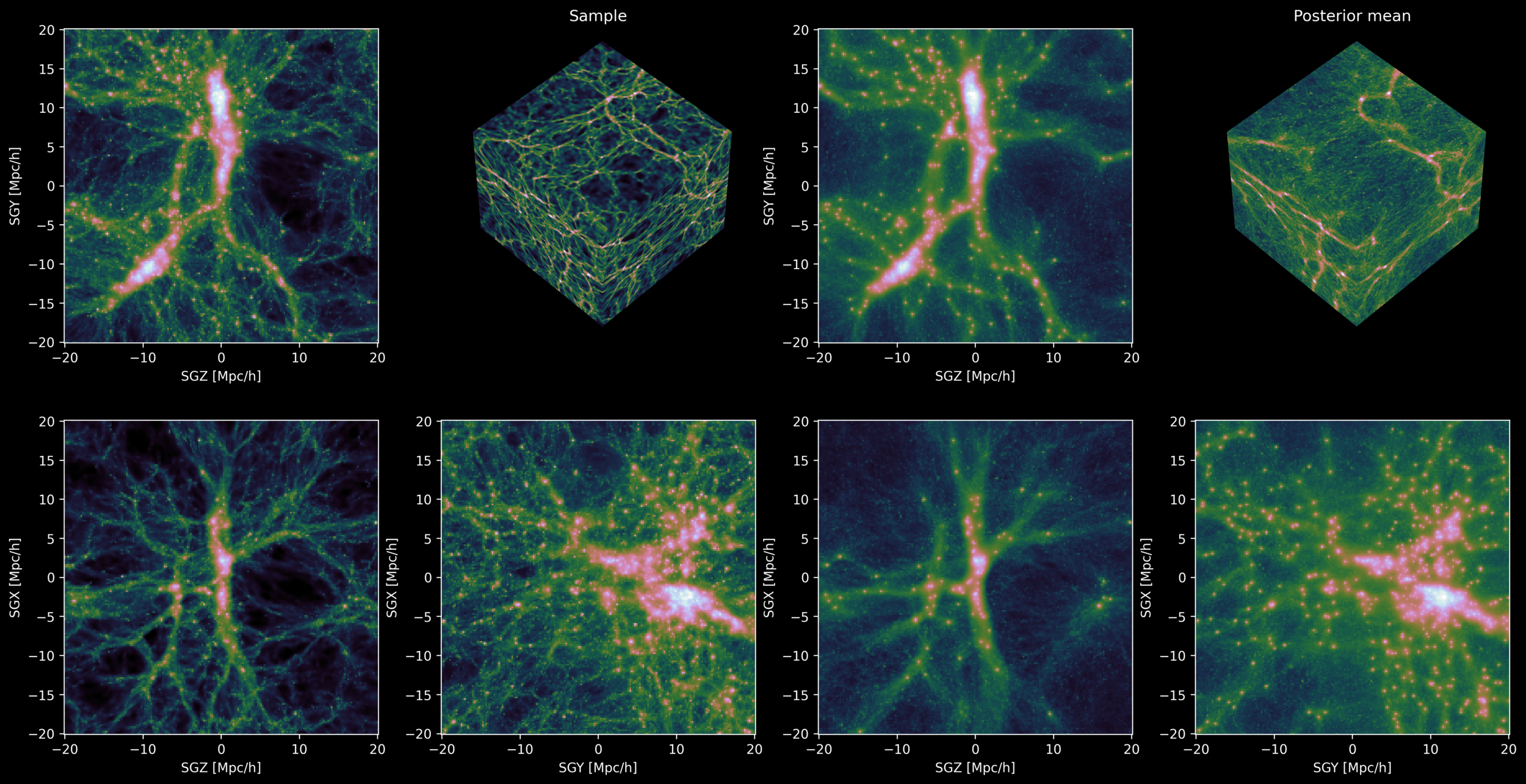
Reconstructing Dark Matter
["A point cloud approach to generative modeling for galaxy surveys at the field level"
Cuesta-Lazaro and Mishra-Sharma
ICML AI4Astro 2023, arXiv:2311.17141]
["3D Reconstruction of Dark Matter Fields with Diffusion Models: Towards Application to Galaxy Surveys"
Park, Mudur, Cuesta-Lazaro et al ICML 2024 AI for Science]
Astrophysics dominates Simulation-based Inference
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
on Simulations
Symmetry preserving architectures
Defining a continuous latent space for feedback
Prompting simulators
Controllable
Simulators
3
Continuous fields
1
Inductive Biases
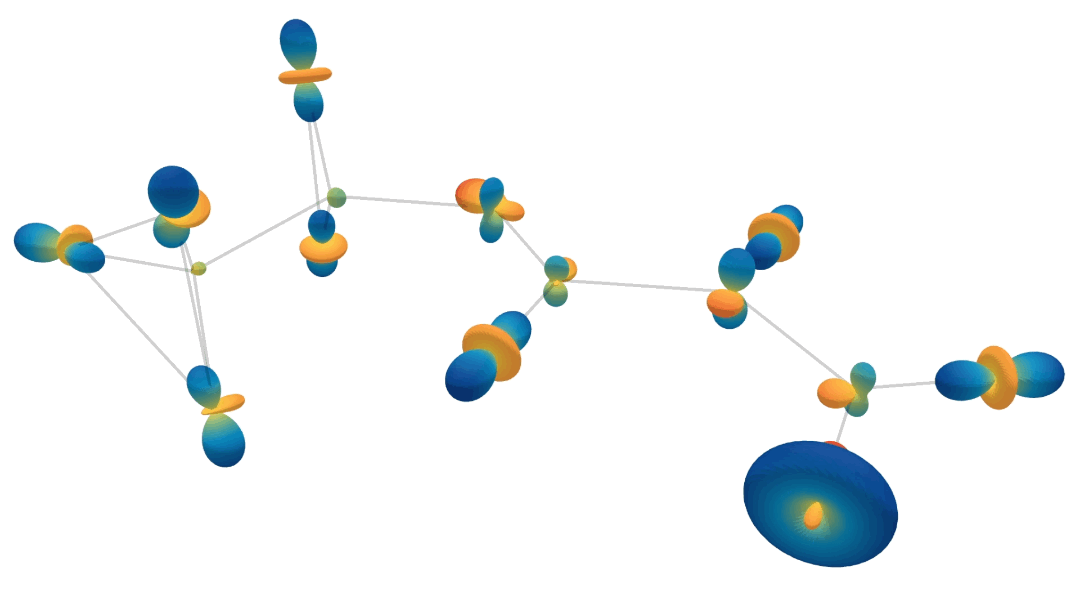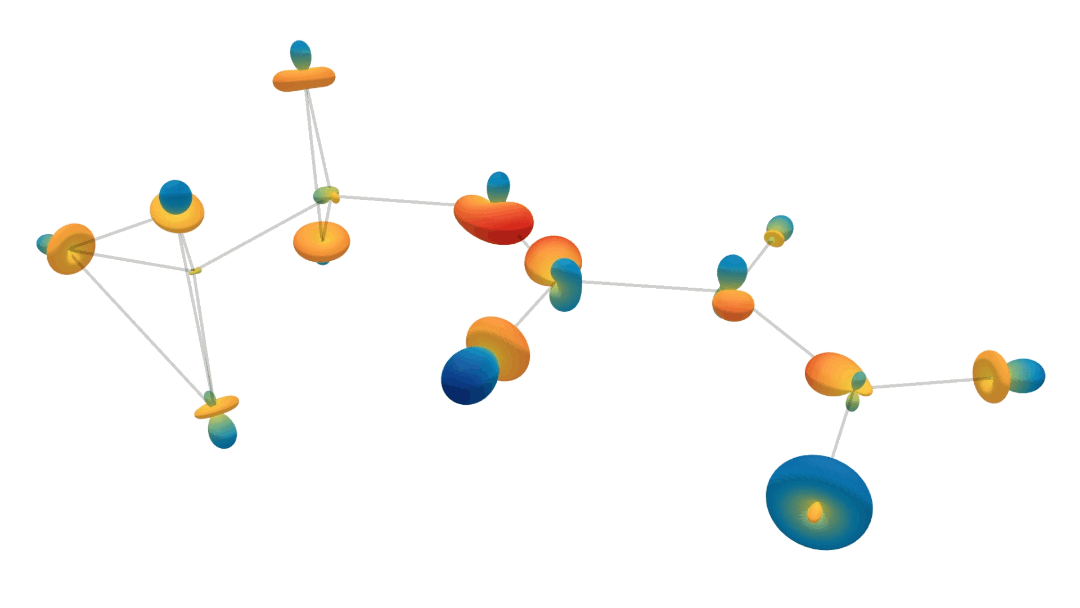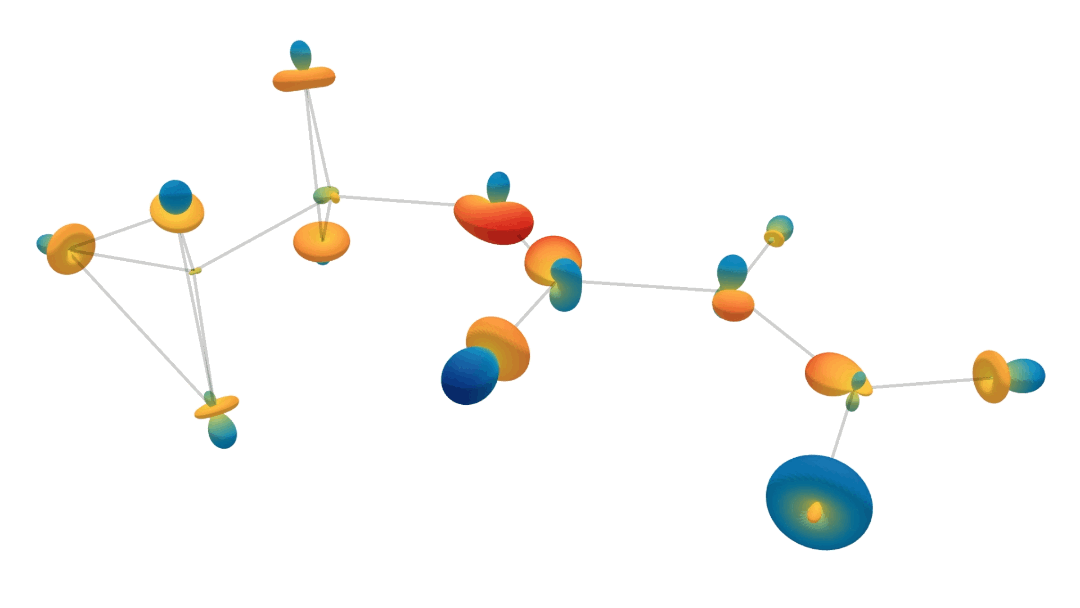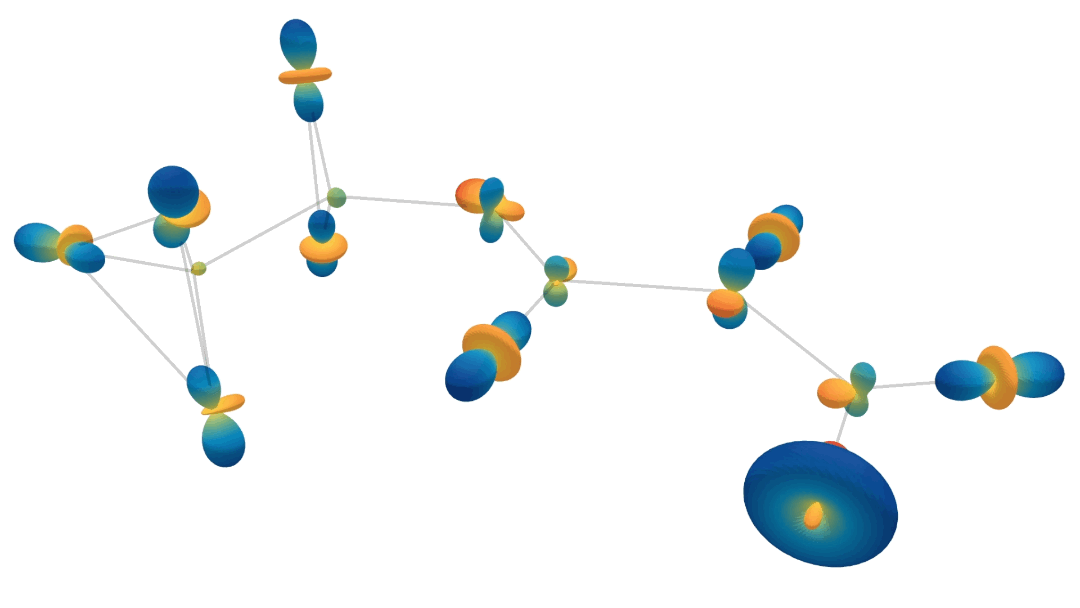
Learning to represent feedback
2
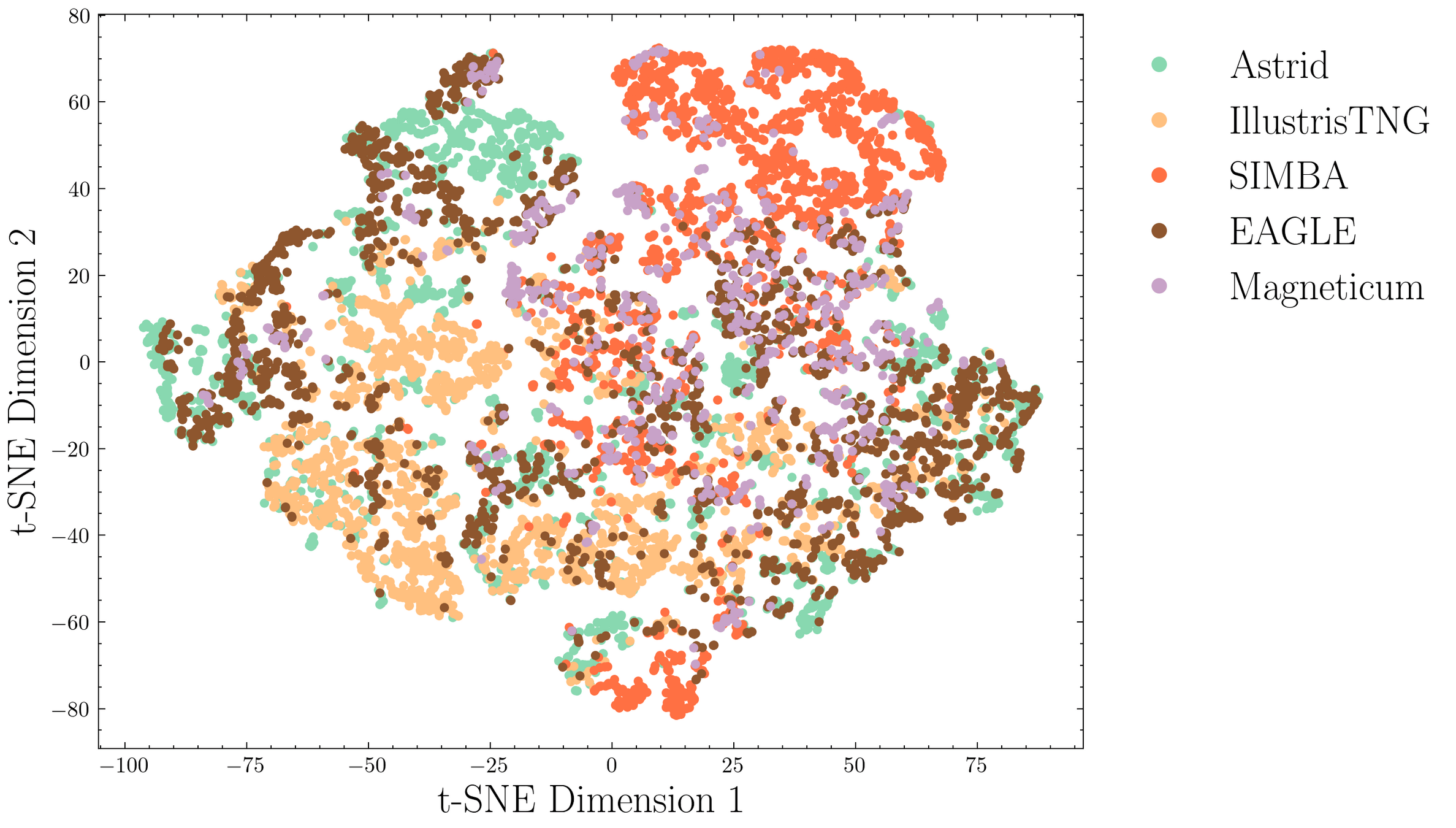
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
The cost of cosmological simulations
AbacusSummit
330 billion particles in 2 Gpc/h volume
\mathcal{O}(100)
60 trillion particles
~ 8TBs per simulation
15M CPU hours
(TNG50 ~100M cpu hours)
\mathcal{O}(10^4)
ML Requirements
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
["A Cosmic-Scale Benchmark for Symmetry-Preserving Data Processing"
Balla, Mishra-Sharma, Cuesta-Lazaro et al
NeurIPs 2024 NuerReps arXiv:2410.20516]
E(3) Equivariant architectures
Benchmark models
["Geometric and Physical Quantities Improve E(3) Equivariant Message Passing" Brandstetter et al arXiv:2110.02905]
Symmetry-preserving ML
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
The bitter lesson by Rich Sutton
The biggest lesson that can be read from 70 years of AI research is that general methods that leverage computation are ultimately the most effective, and by a large margin. [...]
methods that continue to scale with increased computation even as the available computation becomes very great. [...]
We want AI agents that can discover like we can, not which contain what we have discovered.
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
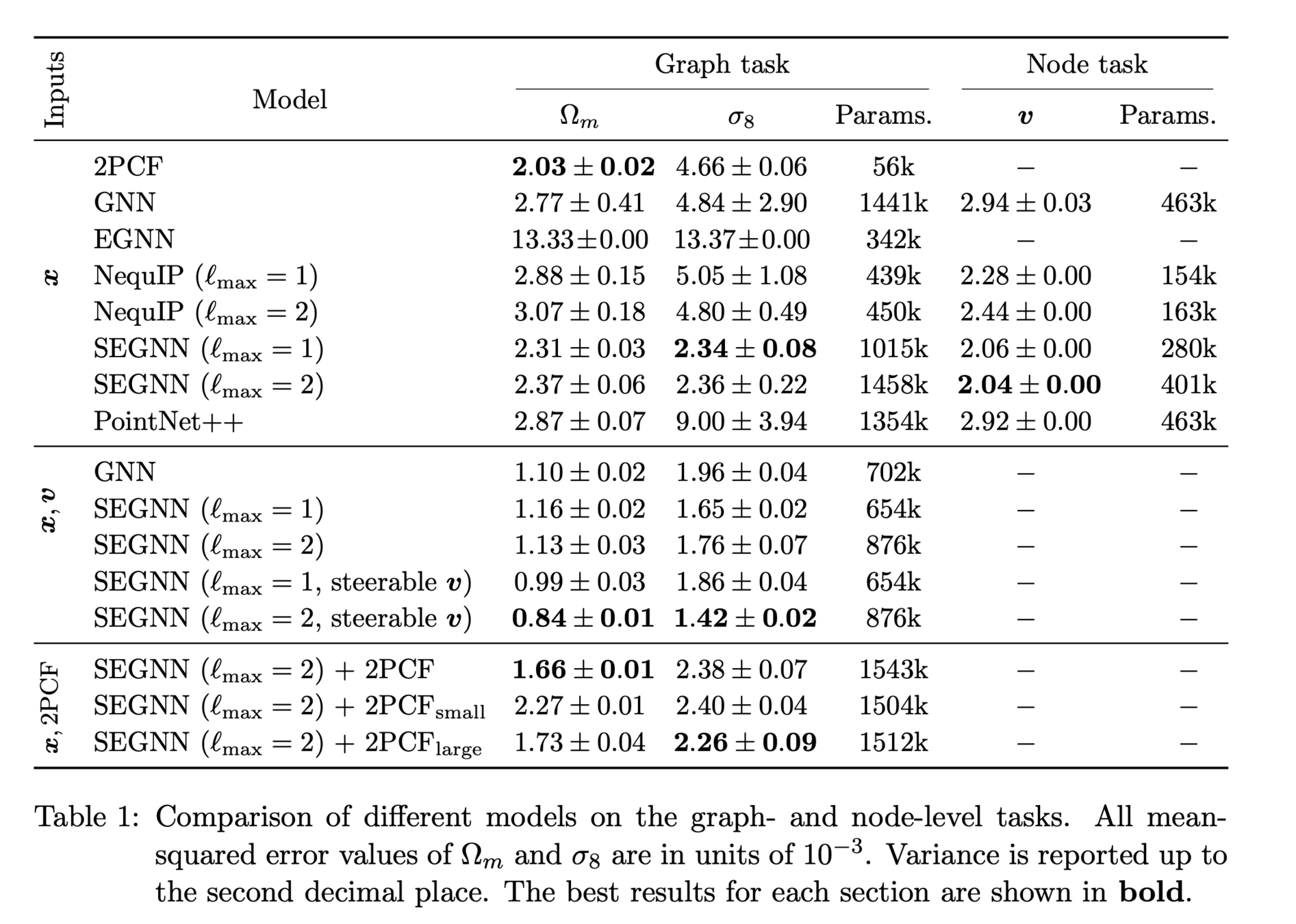
["A Cosmic-Scale Benchmark for Symmetry-Preserving Data Processing"
Balla, Mishra-Sharma, Cuesta-Lazaro et al
NeurIPs 2024 NuerReps arXiv:2410.20516]
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
(MSE errors in units of 1e-3)
Memory scaling point clouds and voxels
h_0
h_1
h_5
h_4
h_2
h_3
h_6
e_{01}
e_{12}
Graph
\mathcal{O}(10^6)
\mathcal{O}(10^8)
Nodes
Edges
3D Mesh
\mathcal{O}(10^{10})
Voxels
Both data representations scale badly with increasing resolution
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
Representing Continuous Fields
(x,y,z,t)
\Psi
\dot \Psi
Continuous in space and time
x500 Compression!
Can we store a simulation inside a neural network?
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
Representation Learning
Informative abstractions of the data
Transfer learning beyond LCDM
Cosmic web Anomaly Detection
Representing baryonic feedback
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
Representation Learning a la gradient descent
Contrastive
Generative
inductive biases
from scratch or from partial observations
Students at MIT are
OVER-CAFFEINATED
NERDS
SMART
ATHLETIC
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
\Omega_m, \sigma_8
Simulator 1
Simulator 2
z
p(
, z)
Dark Matter
Feedback
\Omega_m, \sigma_8
i) Contrastive
Learning the feedback manifold
Baryonic fields
ii) Generative
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
Baryonic fields
Dark Matter
Generative model
Total matter, gas temperature,
gas metalicity
p(
)
, z)
p(
z = f_\theta (
)
Encoder
+
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
p(\mathcal{C},z|
)
z
X-Ray
Gas mass fractions
Gas density profiles
Sunyaev-Zeldovich
Galaxy Properties
Thermal Integrated electron pressure (hot electrons)
Star formation + histories
Stellar mass / halo mass relation
Multi-wavelength observations
FRBs
Integrated electron density
Kinetic Integrated electron density x peculiar velocity
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
Reconstructing dark matter back in time
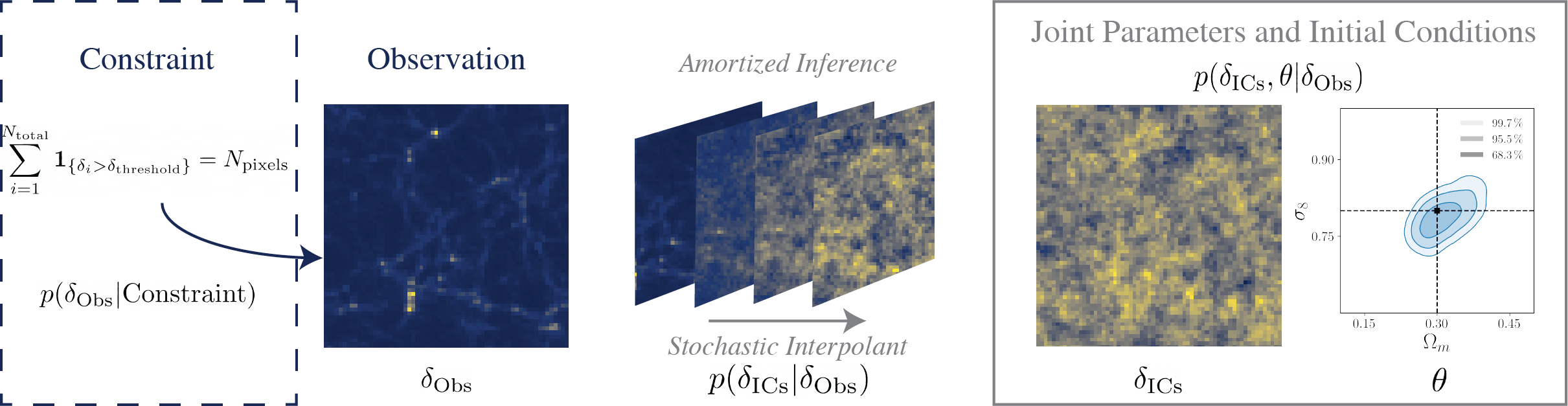
Stochastic Interpolants
NF
p(\delta_\mathrm{ICs}, \theta|\delta_\mathrm{Obs}) =
p(\delta_\mathrm{ICs}|\delta_\mathrm{Obs})
p(\theta|\delta_\mathrm{ICs},\delta_\mathrm{Obs})
["Joint cosmological parameter inference and initial condition reconstruction with Stochastic Interpolants" Cuesta-Lazaro, Bayer, Albergo et al NeurIPs 2024 ML for the Physical Sciences]
Adrian Bayer
Mount Fuji?
Chirag Modi
\frac{dx_t}{dt} = v^\phi_t(x_t)
x_1 = x_0 + \int_0^1 v^\phi_t(x_t) dt
\frac{d p(x_t)}{dt} = - \nabla \left( v^\phi_t(x_t) p(x_t) \right)
Continuous time Normalizing Flows
Continuity Equation
Loss requires solving an ODE!
Diffusion, Flow matching, Interpolants... All ways to avoid this at training time
[Image Credit: "Understanding Deep Learning" Simon J.D. Prince]
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
\frac{dx_t}{dt} = v_\theta(t,x_t)
= (1-t)x_0 + t x_1
v(t,x_t) = \mathbb{E}\left[\partial_t I | x_t=x \right]
Can we regress the velocity field directly?
Turned maximum likelihood into a regression problem!
I(t,x_0,x_1) = x_t = \alpha_t x_0 + \beta_t x_1
\mathcal{L} = \int_0^1 \mathbb{E}_{x_0,x_1} \left[v_\theta(t, x_t) - \partial_t I(t,x_0,x_1) \right] ^2 dt
Interpolant
+ \gamma_t z
Stochastic Interpolant
Expectation over all possible paths that go through xt
["Stochastic Interpolants: A Unifying framework for flows and diffusion" Albergo et al arXiv:2303.08797]
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
p(x_1|x_0)
x_0
?
x_1
s
["Probabilistic Forecasting with Stochastic Interpolants and Foellmer Processes" Chen et al arXiv:2403.10648 (Figure adapted from arXiv:2407.21097)]
Generative SDE
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
Cross-Correlation True ICs | Pred ICs
Guided simulations with fuzzy constraints
Simulate what you need
(and sometimes what you want)
p(\delta_\mathrm{ICs}| \mathrm{Condition})
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
2. A general representation for baryonic feedback may inform galaxy formation modelling
Conclusions
Can we constrain it through multi-wavelength observations?
1. Inductive biases in cosmology can greatly improve constraints
Symmetry preserving architectures: + constraining power and simulation efficiency
Continuous fields: memory efficient data representations and compression methods
3. Cosmological field level inference can be made efficient with generative models
Can generally make simulators more controllable!
Carolina Cuesta-Lazaro IAIFI/MIT @ Flatiron 2024
Flatiron2024
By carol cuesta
