How much do you think we should spend now to cut the risk of a $200 billion catastrophe in half, from 2% per year to 1% per year, for the next 100 years?
pollev.com/chrismakler
How much do you think we should spend now to cut the risk of a $200 billion catastrophe in half, from 2% per year to 1% per year, for the next 100 years?
This will depend on two factors:
How much do you value the future vs. the present?
How do you feel about
risk and uncertainty?
Time and Risk:
Applications and Extensions
Christopher Makler
Stanford University Department of Economics
Econ 50: Lecture 13
Risk Aversion
and Insurance
Expected Value
If a random variable \(X\) takes on values \(x_1,x_2,x_3,...,x_n\) with probabilities \(\pi_1,\pi_2,\pi_3,...,\pi_n\), where the \(\pi\)'s all add up to 1, then the expected value of \(X\) is
\mathbb{E}[X] = \sum_{i = 1}^n \pi_i x_i
= \pi_1x_1 + \pi_2x_2 + \pi_3x_3 + \cdots + \pi_nx_n
Example:
Suppose there is a 50% chance it will rain tomorrow,
If it rains, there is an 80% chance it will rain 10mm,
and a 20% chance it will rain 20mm.
What is the expected value of the amount of rain?
pollev.com/chrismakler
Two ways of framing the same question:
You face a lottery:
\(c_1 = \$16\) with probability \(\pi = {1 \over 4}\)
\(c_2 = \$64\) with probability \((1-\pi) = {3 \over 4}\)
You have $64, and you face a 25% risk of losing $48
What is the expected value of this lottery?
What is your expected loss?
\mathbb{E}[c] = \pi c_1 + (1-\pi)c_2
\mathbb{E}[\text{loss}] = \tfrac{1}{4} \times \$48 = \$12
= \$4 + \$48 = \boxed{\$52}
\mathbb{E}[c] = \$64 - \mathbb{E} = \$64 - \$12 = \boxed{\$52}
What is the expected value of your consumption?
= \tfrac{1}{4} \times \$16 + \tfrac{3}{4} \times \$64
pollev.com/chrismakler
You have $64 and face a 25% chance of losing $48.
We just showed that your expected consumption is $52.
Is this an amount you ever actually consume?
Two ways of framing the same question:
You face a lottery:
You have $64, and you face a 25% risk of losing $48
\mathbb{E}[\text{loss}] = \tfrac{1}{4} \times \$48 = \$12
\mathbb{E}[c] = \boxed{\$52}
Now suppose your value function for money is \(v(c) = \sqrt{c}\).
What is your expected utility?
\mathbb{E}[v(c)] = \pi v(16) + (1-\pi) v(64)
= \tfrac{1}{4}\sqrt{16} + \tfrac{3}{4}\sqrt{64}
= 1 + 6
=7
\(c_1 = \$16\) with probability \(\pi = {1 \over 4}\)
\(c_2 = \$64\) with probability \((1-\pi) = {3 \over 4}\)
utils
Two ways of framing the same question:
You face a lottery:
You have $64, and you face a 25% risk of losing $48
\mathbb{E}[\text{loss}] = \tfrac{1}{4} \times \$48 = \$12
\mathbb{E}[c] = \boxed{\$52}
v(c) = \sqrt{c} \Rightarrow \mathbb{E}[v(c)] = 7 \text{ utils}
\(c_1 = \$16\) with probability \(\pi = {1 \over 4}\)
\(c_2 = \$64\) with probability \((1-\pi) = {3 \over 4}\)
What is your certainty equivalent for this lottery?
pollev.com/chrismakler
u(CE) = \mathbb{E}[v(c)]
\sqrt{CE} \text{ utils} = 7 \text{ utils}
CE = \boxed{\$49}
Two ways of framing the same question:
You have $64, and you face a 25% risk of losing $48
\mathbb{E}[\text{loss}] = \tfrac{1}{4} \times 48 = 12
You face a lottery:
\(c_1 = \$16\) with probability \(\pi = {1 \over 4}\)
\(c_2 = \$64\) with probability \((1-\pi) = {3 \over 4}\)
v(c) = \sqrt{c} \Rightarrow \mathbb{E}[v(c)] = 7 \text{ utils}
\mathbb{E}[c] = \boxed{\$52}
CE = \boxed{\$49}
Buying Insurance against a Loss
Money in good state
Money in bad state
100
20
Suppose you have $100. Life's good.
If your phone breaks, you have to pay $80 to repair the screen, leaving you with $20.
You might want to insure against this loss by buying a contingent contract that pays you $K in the case your phone breaks.
Money in good state
Money in bad state
100
20
You want to insure against this loss by buying a contingent contract that pays you $K in the case you break your screen. Suppose this costs $P.
Now in the good state, you have $100 - P.
In the bad state, you have $20 - P + K.
100 - P
20 + K - P
Budget line
\text{price ratio = }\frac{P}{K - P}
\text{Suppose each dollar of payout costs }\gamma
\text{so buying }K\text{ units costs }P = \gamma K
\text{price ratio = }\frac{P}{K - P}
= \frac{\gamma K}{K - \gamma K}
= \frac{\gamma}{1 - \gamma}
u(c_1,c_2) = \pi v(c_1) + (1-\pi) v(c_2)
MRS = \frac{\partial u(c_1,c_2)/\partial c_1}{\partial u(c_1,c_2)/\partial c_2} = \frac{\pi}{1-\pi} \times \frac{v'(c_1)}{v'(c_2)}
\text{Recall:}
\text{price ratio = }\frac{\gamma}{1 - \gamma}
Note: along the "line of certainty" where \(c_1 = c_2\),
it must be the case that \(v'(c_1) = v'(c_2)\),
so the MRS is just \(\frac{\pi}{1-\pi}\)
MRS = \text{price ratio}
\text{If price ratio = }\frac{\gamma}{1 - \gamma}\text{ and }\gamma = \pi\text{, then tangency condition:}
\Rightarrow \text{ a risk-averse person facing an actuarially fair price will fully insure}
\frac{\pi}{1-\pi} \times \frac{v'(c_1)}{v'(c_2)} = \frac{\pi}{1-\pi}
\frac{u'(v_1)}{u'(v_2)} = 1
u'(c_1) = u'(c_2)
c_1 = c_2
(1+r)c_1 + c_2 = (1+r)m_1 + m_2
How much can you consume in the future if you save all your present income \(m_1\)?
How much can you consume in the present if you borrow the maximum amount against your future income?
FV = c_2 = (1+r)m_1 + m_2
\displaystyle{PV = c_1 = m_1 + {m_2 \over 1 + r}}
Supply of Savings and
Demand for Borrowing
Gross demand = your optimal bundle given interest rate \(r = (c_1^*(r), c_2^*(r))\)
If you want to consume more than your present income at interest rate \(r\),
your demand for borrowing is
\(b(r) = c_1^*(r) - m_1\)
How does this compare to your initial income stream \((m_1,m_2)\)?
If you want to consume less than your present income at interest rate \(r\),
your supply of savings is
\(s(r) = m_1 - c_1^*(r)\)
c_2 = m_2 + (1 + r)(m_1 - c_1)
Inflation and Real Interest Rates
Suppose there is inflation,
so that each dollar saved can only buy
\(1/(1 + \pi)\) of what it originally could:
c_2 = m_2 + \left({1 + r\over 1 + \pi}\right)(m_1 - c_1)
Up to now, we've been just looking at
dollar amounts in both periods
\text{let }\rho = {1 + r \over 1 + \pi} - 1
c_2 = m_2 + (1 + \rho)(m_1 - c_1)
We call \(r\) the "nominal interest rate" and \(\rho\) the "real interest rate"
For low values of \(r\) and \(\pi\), \(\rho \approx r - \pi\)
c_1 + \frac{c_2}{1+r} = m_1 + \frac{m_2}{1 + r}
"Present Value" for two periods
Beyond Two Periods
If you save \(s\) now, you get \(x = s(1 + r)\) next period.
The amount you have to save in order to get \(x\) one period in the future is
s(1 + r) = x
s = {x \over 1 + r}
Remember how we got this...
If you save \(s\) now, you get \(x = s(1 + r)\) next period.
The amount you have to save in order to get \(x\) one period in the future is
s(1 + r) = x
s = {x \over 1 + r}
If you save for two periods, it grows at interest rate \(r\) again, so \(x_2 = (1+r)(1+r)s = (1+r)^2s\)
Therefore, the amount you have to save in order to get \(x_2\) two periods in the future is
s(1 + r)^2 = x_2
s = {x_2 \over (1 + r)^2}
If you save for two periods, it grows at interest rate \(r\) again, so \(x_2 = (1+r)(1+r)s = (1+r)^2s\)
Therefore, the amount you have to save in order to get \(x_2\) two periods in the future is
s(1 + r)^2 = x_2
s = {x_2 \over (1 + r)^2}
If you save for \(t\) periods, it grows at interest rate \(r\) each period, so \(x_t = (1+r)^ts\)
Therefore, the amount you have to save in order to get \(x_t\), \(t\) periods in the future, is
s(1 + r)^t = x_t
s = {x_t \over (1 + r)^t}
Therefore, the amount you have to save in order to get \(x_t\), \(t\) periods in the future, is
s(1 + r)^t = x_t
s = {x_t \over (1 + r)^t}
We call this the present value of a payoff of \(x_t\)
PV(x_t) = {x_t \over (1 + r)^t}
Application: Social Cost of Carbon
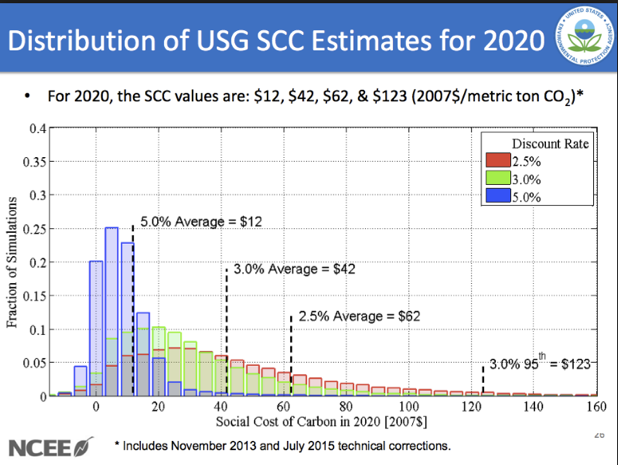
Obama Admin: $45
Uses a 3% discount rate; includes global costs
Trump Admin: less than $6
Uses a 7% discount rate; only includes American costs
PV of $1 Trillion in 2100:
$86B for Obama, $4B for Trump
Risky Assets and Optimal Portfolio Theory
Econ 50 | Fall 25 | Lecture 13
By Chris Makler
Econ 50 | Fall 25 | Lecture 13
We apply the framework of consumer choice theory to the choice of how to allocation money across time, investigating saving and borrowing.
