Review of Univariate Calculus
Christopher Makler
Stanford University Department of Economics
Econ 50: Lecture 2
Answer by 11:35 at pollev.com/chrismakler

Suppose \(a\), \(b\), and \(c\) are strictly positive constants.
Which of the following is a graph of \(ax+by=c\)?
(A)
(B)
(C)
(D)

Again suppose \(a\), \(b\), and \(c\) are strictly positive constants.
Which of the following shows the effect of an increase in the parameter \(a\)?
(A)
(B)
(C)
(D)
The four dashed lines below show the line \(ax+by=c\)
Parallel shift out
Parallel shift in
Pivot out
Pivot in

Again suppose \(a\), \(b\), and \(c\) are strictly positive constants.
Which of the following shows the graph of the implicit function \(a\ln(x) + b\ln(y) = c\)?
(A)
(B)
(C)
(D)
Concave, upward sloping curve
Convex, upware sloping curve
Concave, downward sloping curve
Convex, downward sloping curve
This Week
Wednesday: Univariate & Graphing
Fluency in Math
Derivatives of Functions and their Inverses
The Chain Rule
Linear Functions
Sketching a Function
Section & Friday: Multivariate
Multivariable Functions
Level Sets
Partial Derivatives
Plus: TA intros!
Section starts tonight!
Office Hours Thurs-Fri-Sat
Fluency in Math
Ways of Describing a Model
Verbally
Mathematically
Visually
Diminishing marginal returns:
as you do more of something
(e.g. study)
you get fewer and fewer results
(e.g. more points on an exam)
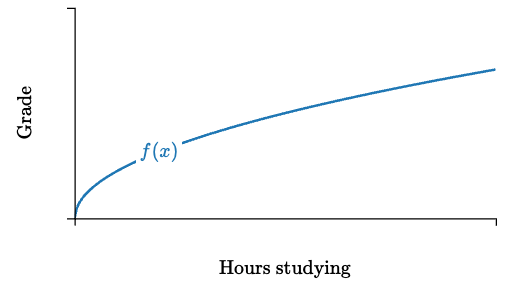
Diminishing marginal returns:
as you do more of something
(e.g. study)
you get fewer and fewer results
(e.g. more points on an exam)
Diminishing marginal returns:
as you do more of something
(e.g. study)
you get fewer and fewer results
(e.g. more points on an exam)
What does "diminishing marginal returns" mean?
Diminishing marginal returns:
as you do more of something
(e.g. study)
you get fewer and fewer results
(e.g. more points on an exam)
What does "diminishing marginal returns" mean?
This has the same sign as \( (a -1) \)
Derivatives of Univariate Functions and their Inverses
Rules for Calculating Derivatives
Constant Rule:
Power Rule:
Natural Log Rule
Multiplication Rule
Chain Rule
Examples of Derivatives
Linear Functions:
Polynomials:
Square Root:
Inverse Functions and their Derivatives
Suppose you have some function
The rate at which \(y\) changes
due to a change in \(x\) is given by the
derivative of this function
The rate at which \(x\) changes
due to a change in \(y\) is given by the derivative of the inverse function
Now consider the inverse of that function
(measured in units of y per units of x)
(measured in units of y per units of x)
(measured in units of x per units of y)
Linear Example
Suppose the distance in miles \((m)\) you travel from home,
as a function of the number of hours driven \((h\)),
is given by the function
How many additional miles do you go in each hour?
How long does it take you to drive an additional mile?
The number of hours it takes you to drive \(m\) miles is given by the inverse of the that function
Non-Linear Example
The Chain Rule
Univariate Chain Rule
Linear Functions
Implicit Functions
Implicit Differentiation
Let's assert that there just is some function \(y(x)\) without solving for it:
If we take the derivative of both sides we get
We can now solve for y'(x):
Sketching a Function
Convexity and Concavity
TA Intros!!!
Multivariable Functions
[INDEPENDENT VARIABLES]
[DEPENDENT VARIABLE]
Multivariable Chain Rule
Total Derivative Along a Path
Total Derivative Along a Path
The total change in the height of the function due to a small increase in \(x\)
The amount \(f\) changes due to the increase in \(x\)
[indirect effect through \(y\)]
The amount \(f\) changes due to an increase in \(y\)
The amount \(y\) changes due to an increase in \(x\)
[direct effect from \(x\)]
Derivative Along a Level Set
Take total derivative of both sides with respect to x:
Solve for \(dy/dx\):
IMPLICIT FUNCTION THEOREM
pollev.com/chrismakler

Consider the multivariable function
What is the slope of the level set passing through the point (1, 5)?
Consider the multivariable function
What is the slope of the level set passing through the point (1, 5)?
Slope of level set = —
Production Functions
Production Functions
A mathematical form describing how much output is produced as a function of inputs.
Labor \((L)\)
Capital \((K)\)
Production Function \(f(L,K)\)
Output (\(q\) or \(x\))
Lecture 2: Production Functions
Labor
Fish
🐟
Capital
Coconuts
🥥
[GOODS]
⏳
⛏
[RESOURCES]
Unit I: Scarcity and Choice
Economics is the study of how
we use scarce resources
to satisfy our unlimited wants
Resources
Goods
Happiness
🌎
⌚️
🤓
Isoquants
Economic definition: if you want to produce some amount \(q\) of output, what combinations of inputs could you use?
Mathematical definition:
level sets of the production function
Isoquant: combinations of inputs that produce a given level of output
Isoquant map: a contour map showing the isoquants for various levels of output
pollev.com/chrismakler

What happens to isoquants after an improvement in technology?
Marginal Products of Labor and Capital
Economic definition: how much more output is produced if you increase labor or capital?
Mathematical definition:
partial derivatives of the production function
These are both rates: they are measured in terms of units of ouptut per unit of input.
pollev.com/chrismakler

Consider the production function
What is the expression for the marginal product of labor?
Marginal Rate of Technical Substitution (MRTS)
Economic definition: the rate at which a producer can substitute one input for another while keeping output at the same level
Mathematical definition: slope of an isoquant
Recall: by implicit function theorem,
the slope of a level set is given by
Therefore the formula for the MRTS is
(absolute value)
Labor (L)
Capital (K)
Intuition behind the formula for the MRTS
Example: Cobb-Douglas Production Function
Summary
So far we've modeled an important economic activity
using multivariable calculus.
We looked at the economic meaning for
various properties of the production function:
Partial Derivatives
Marginal Products
Level Sets
Isoquants
Slope of a Level Set
Marginal Rate of Technical Substitution
In section and on Friday, we'll analyze how
different functional forms can be used to model different kinds of technologies.
Econ 50 | Lecture 02
By Chris Makler
Econ 50 | Lecture 02
Review of Univariate Calculus
- 724



