pollev.com/chrismakler

What color shirt am I wearing?
pollev.com/chrismakler

Suppose Chuck can use labor
to produce fish (good 1)
or coconuts (good 2).
If we plot his PPF in good 1 - good 2 space, what are the units of Chuck's MRT?
Suppose Chuck could initially produce 3 fish (good 1) or 2 coconuts (good 2)
in an hour.
He gets better at fishing, which allows him to produce 4 fish per hour.
What effect will this have on his MRT?
CHECK YOUR UNDERSTANDING
pollev.com/chrismakler

Christopher Makler
Stanford University Department of Economics
Econ 50: Lecture 4 (Part II; Part I was on video)
Resource Constraints and Production Possibilities
Today's Agenda
Part 1: From production functions to the PPF
Part 2: The slope of the PPF
Getting situated in "Good 1 - Good 2 space"
Resource constraints and the PPF
Deriving the equation of the short-run PPF
The Marginal Rate of Transformation
Relationship between MPL and MRT
Deriving the expression for the MRT
using the implicit function theorem
Good 1 - Good 2 Space
Two "Goods" (e.g. fish and coconuts)
A bundle is some quantity of each good
Can plot this in a graph with \(x_1\) on the horizontal axis and \(x_2\) on the vertical axis
Good 1 - Good 2 Space
What tradeoff is represented by moving
from bundle A to bundle B?
ANY SLOPE IN GOOD 1 - GOOD 2 SPACE
IS MEASURED IN
UNITS OF GOOD 2 PER UNIT OF GOOD 1
ANY SLOPE IN GOOD 1 - GOOD 2 SPACE
IS MEASURED IN
UNITS OF GOOD 2 PER UNIT OF GOOD 1
TW: HORRIBLE STROBE EFFECT!
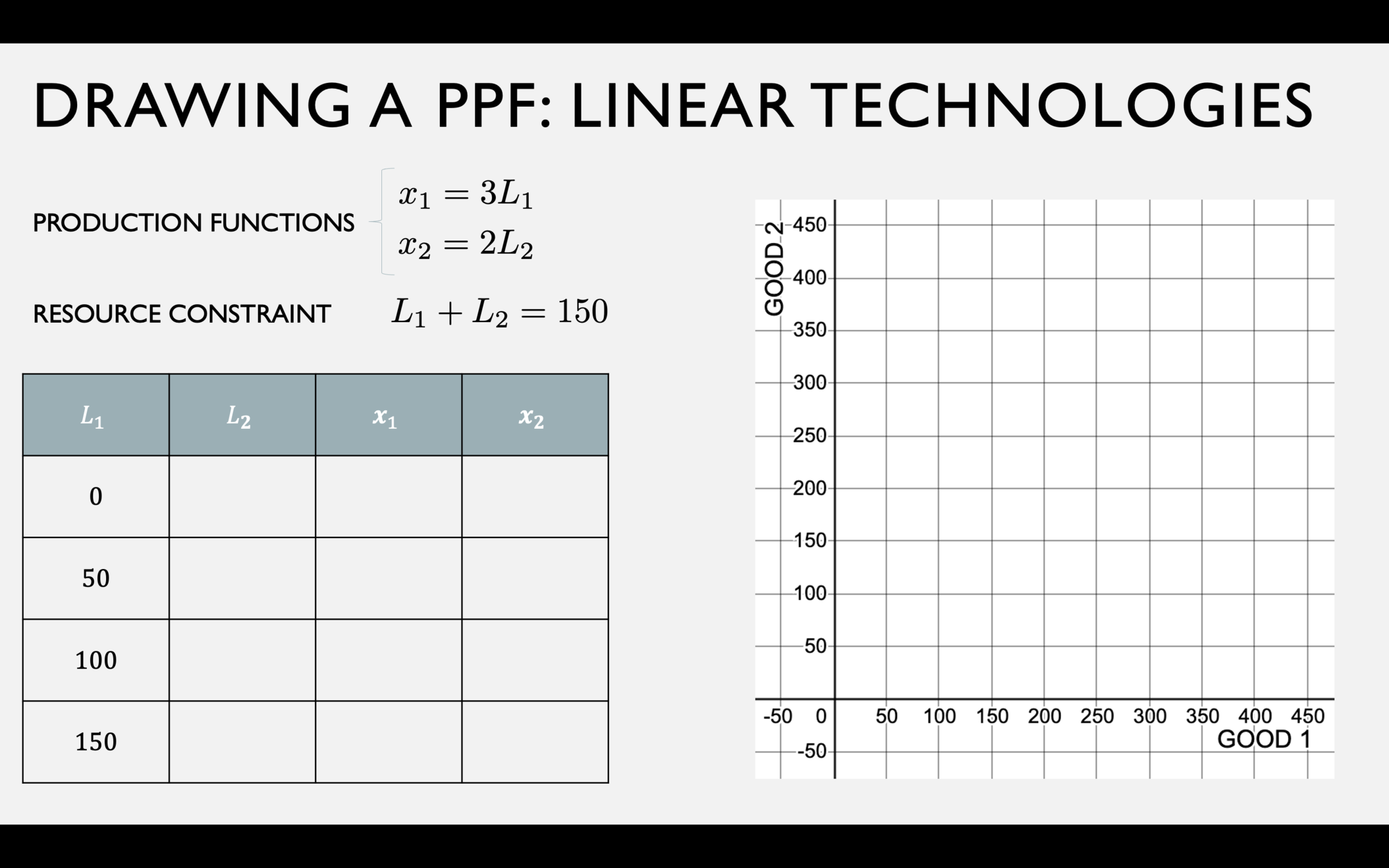
PPF


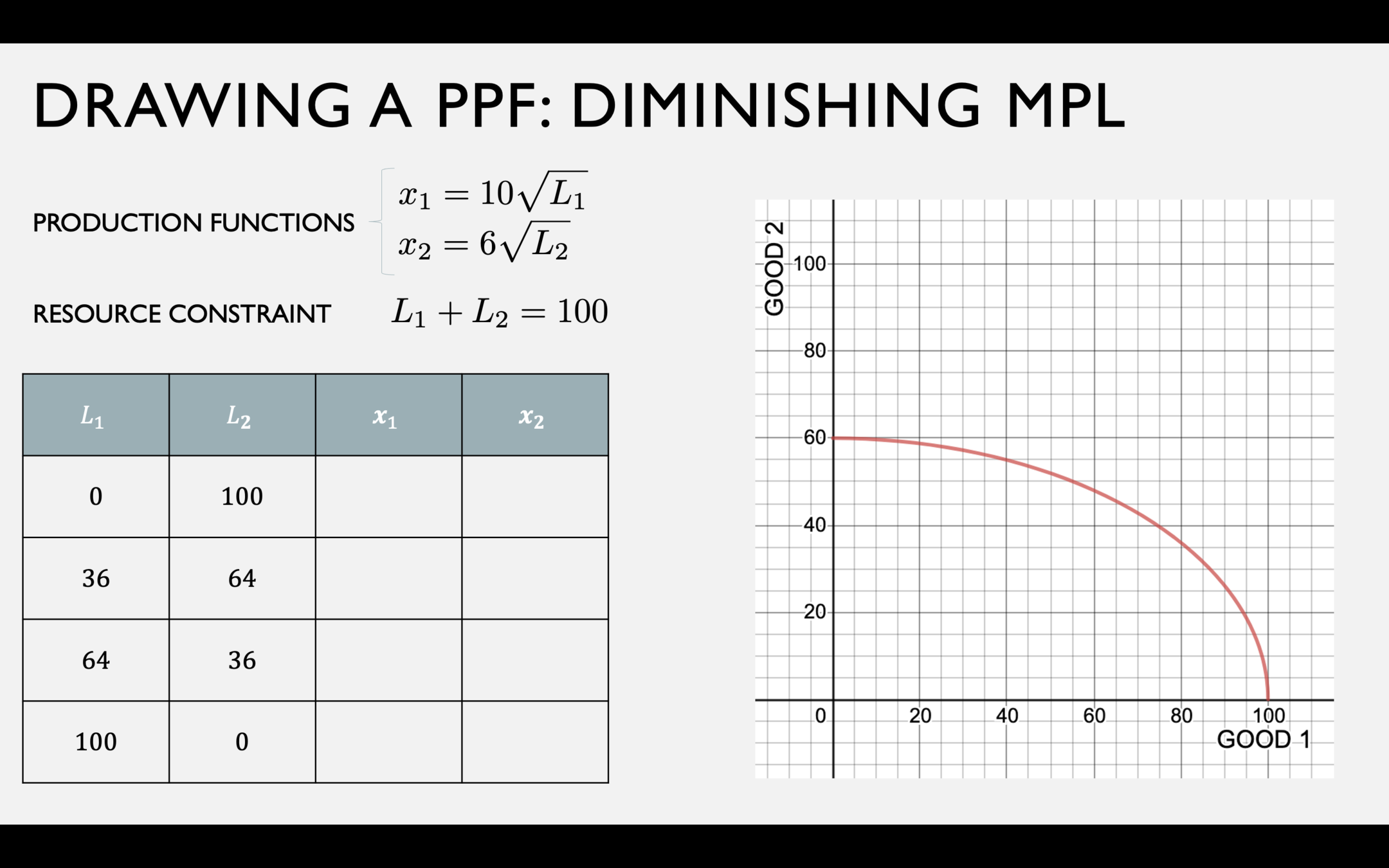
PPF


Part 2: The MRT
Mathematical Aside
Suppose you have some function
The rate at which \(y\) changes
due to a change in \(x\) is given by the
derivative of this function
The rate at which \(x\) changes
due to a change in \(y\) is given by the derivative of the inverse function
Now consider the inverse of that function
(measured in units of y per units of x)
(measured in units of y per units of x)
(measured in units of x per units of y)
Mathematical Aside
Suppose the distance in miles \((m)\) you travel from home,
as a function of the number of hours driven \((h\)),
is given by the function
How many additional miles do you go in each hour?
How long does it take you to drive an additional mile?
The number of hours it takes you to drive \(m\) miles is given by the inverse of the that function
Mathematical Aside
Suppose the amount of fish \((x_1)\) you can produce using \(L_1\) hours of labor is given by
How many additional fish do you catch in the \(L_1^\text{th}\) hour?
How many additional hours does it take to catch the \(x_1^\text{th}\) fish?
The number of hours it takes you to get \(x_1\) fish is given by the inverse of the that function
Mathematical Aside
Slope of the PPF:
Marginal Rate of Transformation (MRT)
Rate at which one good may be “transformed" into another
...by reallocating resources from one to the other.
Opportunity cost of producing an additional unit of good 1,
in terms of good 2
Note: we will generally treat this as a positive number
(the magnitude of the slope)

This is just a level set of the function \(f(x_1,x_2) = {1 \over 3}x_1 + {1 \over 2}x_2\)
By the implicit function theorem:
Suppose we're allocating 100 units of labor to fish (good 1),
and 50 of labor to coconuts (good 2).
Now suppose we shift
one unit of labor
from coconuts to fish.
How many fish do we gain?
100
98
300
303
How many coconuts do we lose?
Relationship between MPL's and MRT
Fish production function
Coconut production function
Resource Constraint
PPF

This is just a level set of the function \(f(x_1,x_2) = \)
By the implicit function theorem:
Total labor required to produce the bundle \((x_1,x_2)\)
\(L_1(x_1) + L_2(x_2)\)
\({1 \over 3}x_1 + {1 \over 2}x_2\)
Recall: \(MP_{L1} = {dx_1 \over dL_1}, MP_{L2} = {dx_2 \over dL_2}\)

This is a level set of the function \(f(x_1,x_2) = {1 \over 100}x_1^2 + {1 \over 36}x_2^2\)
By the implicit function theorem:

Could you do this using the MPL method?
Remember: we need to express this in terms of \(x_1\) and \(x_2\)!
Important Notes
The MRT is the slope of the PPF at some output combination \((x_1,x_2)\)
You should therefore write it in terms of \(x_1\) and \(x_2\), not \(L_1\) and \(L_2\).
You can use two methods to find the MRT:
the ratio of the MPL's, or the implicit function theorem.
CHECK YOUR UNDERSTANDING
Chuck has \(\overline L = 8\) total hours of labor,
and the production functions
\(x_1 = 2 \sqrt{L_1}\) and \(x_2 = 4\sqrt{L_2}\).
What is his MRT if he spends
half his time producing each good?
pollev.com/chrismakler

Charlene has the PPF given by
\(2x_1^3 + 3x_2^4 = 1072\)
What is her MRT if she produces the output combination \((8,2)\)?
Chuck has \(\overline L = 8\) total hours of labor,
and the production functions
\(x_1 = 2 \sqrt{L_1}\) and \(x_2 = 4\sqrt{L_2}\).
What is his MRT if he spends
half his time producing each good?
Charlene has the PPF given by
\(2x_1^3 + 3x_2^4 = 1072\)
What is her MRT if she produces the output combination \((8,2)\)?
If \(L_1 = L_2\) then this is just 2!
Everything is given in terms of L,
so let's use the \(MP_L\) formula:
Since \(x_1^2 = 64\) and \(x_2^3 = 8\), this is 4.
We have the PPF in terms of \(x_1\) and \(x_2\),
so let's use the implicit function theorem:
- Resource constraints + production functions = production possibilities
- The MRT (slope of PPF) is the opportunity cost of producing good 1
(in terms of good 2) - If there is only one input (labor), the MRT is the ratio of the MPL's
- In general, best way to find the MRT is by using the implicit function theorem
- Homework due Saturday night; includes a more complicated PPF than you've seen!
- Next topic: preferences over bundles
Key Takeaways
Econ 50 | Lecture 04 (Spring 2024 - live portion)
By Chris Makler
Econ 50 | Lecture 04 (Spring 2024 - live portion)
Resource Constraints and Production Possibilities
- 806



