Welcome &
Math Review
Christopher Makler
Stanford University Department of Economics
Econ 50: Lecture 1
Today's Agenda
Part 1: Course Overview
Part 2: Math Review
Who is the Econ 50 teaching team?
Why is this class important?
What is this course about?
When will we study each topic?
How do we all succeed?
Multivariable Functions
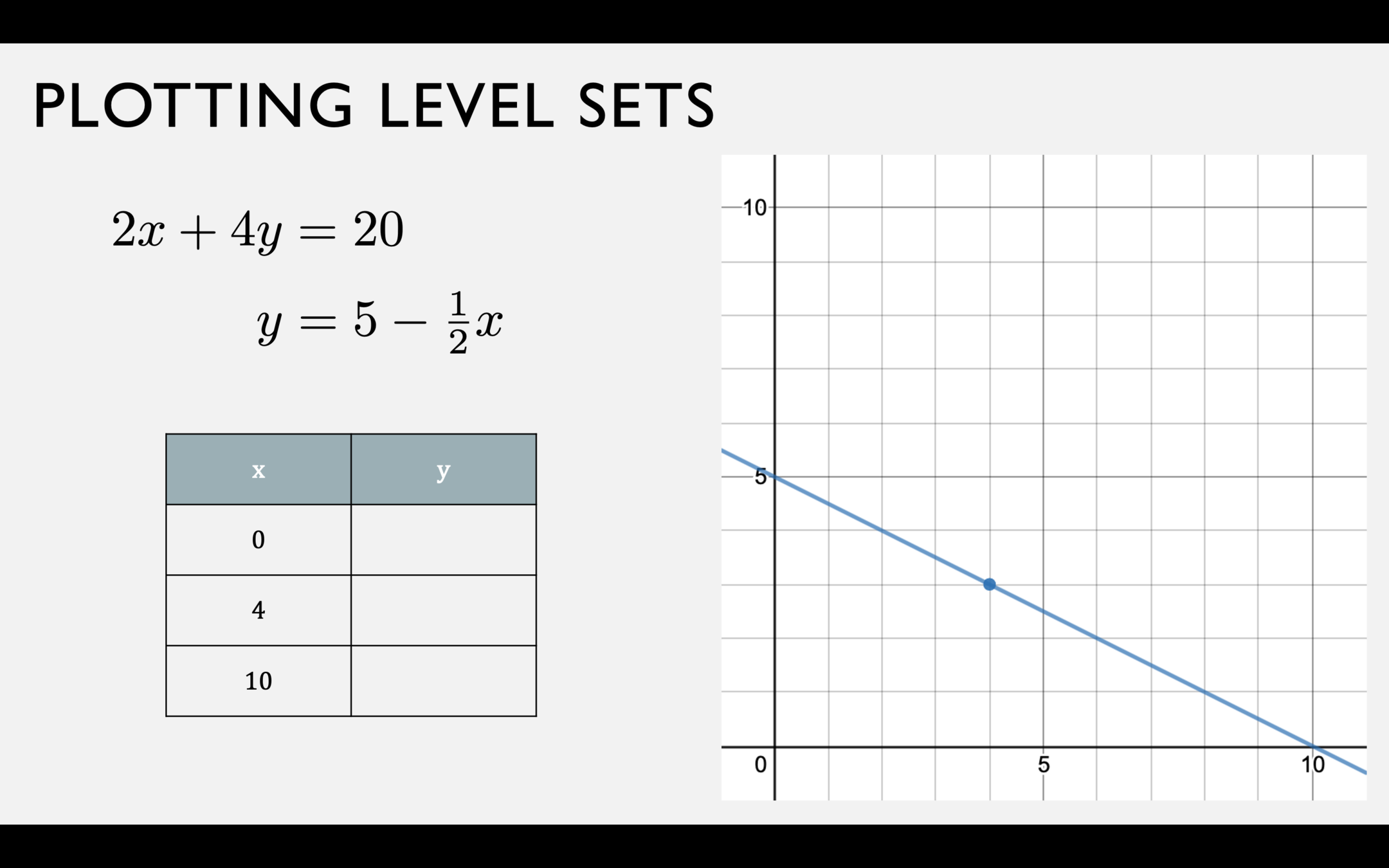
Level Sets
Partial Derivatives
The Chain Rule
Implicit Differentiation
Who
Chris Makler
- B.A.: Humanities, Yale
- Ph.D.: Economics, Penn
(search & matching theory)
- 10 years in the education technology industry
- Teaching Econ 50 & 51 since 2015
- Office: Landau Econ Building, Room 144
Welcome to Econ 50!
Frank Wolak
Director of Undergraduate Studies
wolak@stanford.edu
Welcome to the Econ Major!
Laura Quirarte
Undergraduate Student Service Officer
lauraq@stanford.edu
TA Intros
Alex
Bing
Yunus
Michelle
Econ Department Peer Advising
Other Resources
VPTL Peer Tutoring
Let's get to know you!
pollev.com/chrismakler
Why are you here?
"Individual consumer and firm behavior
under perfect competition.
The role of markets and prices in a decentralized economy.
Monopoly in partial equilibrium.
Economic tools developed from multivariable calculus using partial differentiation
and techniques for constrained and unconstrained optimization."
It's probably not the sexiness of the course description:
Econ 50 unlocks Econ 51/52, plus...
- History of Financial Crises (Econ 110)
- Money and Banking (Econ 111)
- Decision Modeling and Information (Econ 137)
- Environmental Economics and Policy (Econ 155)
- Economic, Legal, & Political Analysis of Climate-Change Policy (Econ 159)
- Microeconomics (PublPol 301A/IPS204A)
- Economic Analysis (MS&E 241)
- Climate Policy Analysis (MS&E 294)
- Energy Policy Analysis (MS&E 295)
- British Economic Policy since World War II (OSPOxfrd 45)
- Poverty and Policies in Developing Economies (PublPol 184)
Add 102A and you unlock...
Add 102B and you unlock...
- Economics of Health and Medical Care (Econ 126, BioMed 156/256, HRP 256)
- Finance for Non-MBA's (Econ 135, MS&E 245G)
- Behavioral Economics (Econ 178)
- Economics of Health Improvement in Developing Countries (Econ 127, Med 262)
- Economics of Education (Econ 146)
- Economic Policy Analysis (Econ 150, PubPol 104/204)
So why is this course
a prerequisite
for so many others?
Ways to Think about Learning
Strategic:
"knowing when" - given an unstructured problem, which model/framework is most relevant?
Schematic:
Procedural:
Declarative:
"knowing why" - how do different concepts/models relate to one other?
"knowing how" - given a well-defined problem, ability to follow correct procedure to solve it
"knowing that" - facts and figures, vocabulary
Goals of the Course
Strategic:
Develop rigorous approach to economic modeling; understand how assumptions map into conclusions.
Schematic:
Procedural:
Declarative:
Understand the relationships between
words, math, and graphs.
Learn the techniques of
optimization, equilibrium, and comparative statics.
Know the definitions of key economic terms.
The overall goal of this course is to prepare you
for all the courses -- and jobs -- that build upon this material...
...by providing you with technical training to solve problems...
...and the ability to take an unstructured situation in the real world
and convert it into a structured, solvable problem.
It's not about the particular models
we're looking at in this class.
It's about learning how to use
the "building blocks" of economic models
to construct models of things you're interested in.
What
Three Fundamental Tools of Analysis
Optimization
Given a fixed set of circumstances (prices, technology, preferences), how do economic agents (consumers, firms) make choices?
Comparative Statics
How do changes in circumstances (changing prices, shifting technology, preferences, etc.) translate into changes in behavior?
Equilibrium
How do economic systems converge toward certain outcomes?
Consumer Theory
The Building Blocks of Economic Models
Lectures 2-8
Faced with a budget constraint,
how will a consumer choose
to allocate their income?
How does their optimal choice change when prices or income change?
Theory of the Firm
The Building Blocks of Economic Models
Lectures 9-11
How do firms choose how much to produce, and how to produce it?
How do competitive firms respond to changes in input and output prices?
Market Equilibrium
The Building Blocks of Economic Models
Lectures 12-13
How does a system converge
to an equilibrium?
Bring (many) consumers and producers together and analyze markets.
More Complicated Models
The Building Blocks of Economic Models
Lectures 14-18
How do taxes and subsidies affect markets?
How do competitive markets differ from situations where firms have market power?
How does the short run
differ from the long run?
Sketch of General Equilibrium theory
Textbooks and Other Resources
Textbook: Varian,
Intermediate Microeconomics:
A Modern Approach
(any edition is fine)
My own interactive lecture notes (linked in quizzes)
UCSD Videos ($10 for the year; link in syllabus)
When
Sunday
Reading and quiz for Monday's lecture
Wednesday
Lecture; do second half of problem set exercises
Thursday & Friday
Section; office hours
Weekly Rhythm (Suggested)
Tuesday
Reading and quiz for Wednesday's lecture
Monday
Lecture; do first half of problem set exercises
Saturday
Review material from the week
Do practice exam problems
Finish & hand in problem set
Weeks 1-4
Consumer Theory
Wed, November 16
Midterm 2
Weeks 9-10
Market Power; Long-Run Equilibrium
Quarter Rhythm
Weeks 5-8
Theory of the Firm; Short-Run Competitive Equilibrium
Mon, October 24
Midterm 1
Fri, December 16
Final Exam
8:30am
Thanksgiving Break
Missing Exams
-
Exams are worth 65% of your grade. Due to multiple honor code violations during COVID, we are not giving students exams to take in isolation: if you miss an exam, for whatever reason, you miss the exam. We are having 3 exams to make it so that missing one exam is less of a big deal.
-
If you take all 3 exams:
-
lower midterm score is 10% of your grade
-
higher midterm score is 20% of your grade
-
final exam is 35% of your grade
-
-
If you miss one of the midterms:
-
the remaining midterm counts is 25% of your grade
-
final exam is 40% of your grade
-
-
If you miss both midterms, you must withdraw from the class (second midterm is week 8)
-
If you take at least one midterm but miss the final: you will automatically get an Incomplete.
We will work to resolve Incompletes as quickly as possible.
Wed, November 16
Midterm 2
Mon, October 24
Midterm 1
Fri, December 16
Final Exam
8:30am
THESE ARE THE EXAM DATES.
DO NOT SCHEDULE VOLUNTARY TRAVEL THAT FORCES YOU TO MISS AN EXAM!!!
PUT THEM IN YOUR CALENDAR.
How
Please be fully present in lecture.
No phones.
No tablets.
No laptops.
I'm not a monster. There will be a break in the middle of each class to connect with your digital world.
Before Lecture
- Read the textbook and take online quizzes on the major points to be prepared for learning in lecture
Lecture
- Presents new ideas
- Illustrate those ideas with simple examples
After Lecture
- Exercises for each lecture are designed to help you understand nuance
- More complex examples and applications than in lectures; work on connecting the dots
After Each Unit
- Exam questions will ask you to apply concepts from lecture to new situations you haven't seen before.
Grading Policy
-
This course is not graded on a curve.
If everyone gets an A, everyone gets an A; if everyone gets a B, everyone gets a B.
Grade cutoffs are given on the syllabus (90-100 = A, 80-89 = A-, etc.) -
Reading quizzes: 5% of your grade. One for each lecture; lowest 4 dropped.
-
In-class polls: 5% of your grade. Graded for completion, not correctness; so low stakes!
However, misrepresenting your presence will result in a grade of 0 for the quarter.
Please go to pollev.com/chrismakler
but do not yet answer the question.
The question is:
"What is 2 feet plus 2 inches, in inches?"
Grading Policy
-
This course is not graded on a curve.
If everyone gets an A, everyone gets an A; if everyone gets a B, everyone gets a B.
Grade cutoffs are given on the syllabus (90-100 = A, 80-89 = A-, etc.) -
Reading quizzes: 5% of your grade. One for each lecture; lowest 4 dropped.
-
In-class polls: 5% of your grade. Graded for completion, not correctness; so low stakes!
However, misrepresenting your presence will result in a grade of 0 for the quarter. -
Problem sets: 25% of your grade. One for each week, except Week 8.
-
Each exercise (including old exam questions) is worth 3 points.
-
You do not have to do them all. Recommend doing 4-5 problems.
-
Full credit (100 points total) for ~11 points per problem set.
-
Maximum 15 points per problem set.
-
-
Exams: 65% of your grade.
Course Web Sites
All content is posted/linked within Canvas.
Each week has its own module with everything you need to know about that week.
Please use Ed Discussions to ask questions (not email).
Please upload your homework to Gradescope by 8am the morning after it's due.
Advice for You from Former Students (from course evals)
"Be prepared for the psets to be fairly more difficult than the examples worked out during lecture.
Sometimes there might be a disconnect between lecture and psets, too."
| "Class is difficult, but there are so many resources available to help you. Make use of office hours." |
"It's a lot of work, but if you stay on top of it, you'll be fine.
Definitely recommend doing all the psets and as many past exam questions as you can.
Makler's exam kinda made me want to cry, but everyone walked out kinda wanting to cry, so it's okay, probably."
"Organized, streamlined, and despairingly efficient.
This class crunches through concepts and ideas faster than you can get a good grip of them.
Makler is very approachable with questions, however, even if he memes on us a lot."
"...If you can, take the course together with your friends; they may be a great resource in helping you
grasp the course concepts! If you decide to take ECON 50, I hope you have a great time
and that you find a close-knit community of fellow enthusiasts of Economics."
The Small Print
- Names and pronouns
- Students with documented disabilities
- Stanford University Honor Code
- Econ Department syllabus
- Humor gone wrong
Office Hours
- Come to office hours!
- Try your hand at the homework before coming to office hours; don't just come and do the homework in front of me. Then come with points of confusion and we'll talk through it.
- This might sound intimidating, but...
10 Minute Break
Math Review
Multivariable Functions
Level Sets
Partial Derivatives
Chain Rule
Implicit Differentiation
Multivariable Functions
x
f()
z = f(x,y)
y
z
[INDEPENDENT VARIABLES]
[DEPENDENT VARIABLE]
\text{Level set for }z=\{(x,y)|f(x,y)=z\}
\displaystyle{{df \over dx} = \lim_{\Delta x \rightarrow 0} {f(x + \Delta x) - f(x) \over \Delta x}}
\displaystyle{{\partial f \over \partial x} = \lim_{\Delta x \rightarrow 0} {f(x + \Delta x, y) - f(x, y) \over \Delta x}}
\displaystyle{{\partial f \over \partial y} = \lim_{\Delta y \rightarrow 0} {f(x, y + \Delta y) - f(x, y) \over \Delta y}}
Univariate Chain Rule
\text{Example: }h(x)=(3x + 2)^2
h(x)=f(g(x))
{dh \over dx} = {df \over dg} \times {dg \over dx}
f(g)=g^2
g(x)=3x+2
Multivariable Chain Rule
\text{Example: }h(x,y)=(3x+y)^2
h(x,y)=f(g(x,y))
{\partial h \over \partial x} = {df \over dg} \times {\partial g \over \partial x}
f(g)=g^2
g(x)=3x+y
Total Derivative Along a Path
\text{How does }f(x,y)\text{ change along a path?}
\Delta f \approx
\displaystyle{{\partial f \over \partial x} \times \Delta x}
\displaystyle{{\partial f \over \partial y} \times \Delta y}
+
\text{Suppose the path is defined by some function }y(x):
\Delta f \approx
\displaystyle{{\partial f \over \partial x} \times \Delta x}
\displaystyle{{\partial f \over \partial y}}
+
\displaystyle{\times {dy \over dx}}
\displaystyle{\times \Delta x}
\displaystyle{\Delta f \over \Delta x} \approx
\displaystyle{{\partial f \over \partial x}}
\displaystyle{{\partial f \over \partial y}}
+
\displaystyle{\times {dy \over dx}}
Total Derivative Along a Path
\displaystyle{\Delta f \over \Delta x}\ \ \ \ \ \ \approx
\displaystyle{{\partial f \over \partial x}}
\displaystyle{{\partial f \over \partial y}}
+
\displaystyle{\times\ \ \ \ \ \ {dy \over dx}}
The total change in the height of the function due to a small increase in \(x\)
The amount \(f\) changes due to the increase in \(x\)
[indirect effect through \(y\)]
The amount \(f\) changes due to an increase in \(y\)
The amount \(y\) changes due to an increase in \(x\)
[direct effect from \(x\)]
y(x)=4-0.4x
Derivative Along a Level Set
f(x,y)=z
Take total derivative of both sides with respect to x:
Solve for \(dy/dx\):
\displaystyle{{\partial f \over \partial x}}
\displaystyle{{\partial f \over \partial y}}
+
\displaystyle{\times \ \ {dy \over dx}}
=
0
\displaystyle{{dy \over dx}}
= -
\displaystyle{{\partial f \over \partial x}}
\displaystyle{{\partial f \over \partial y}}
IMPLICIT FUNCTION THEOREM
Econ 50 | Spring 22 | Lecture 1
By Chris Makler
Econ 50 | Spring 22 | Lecture 1
Fall 2021 Math Review
