Game Theory II:
Dynamic Games
Christopher Makler
Stanford University Department of Economics
Econ 51: Lecture 10
Big Ideas
Today: extend notion of best-response (Nash) equilibrium to the class of dynamic games with complete & perfect information.
As we saw with Stackelberg vs. Cournot, the same actions can result in different equilibria if games are played sequentially vs. simultaneously.
As we saw with the model of collusion in cartels,
being involved in an ongoing relationship allows cooperation
of a sort that is impossible in a "one-shot" game.
Big Ideas
Today: extend notion of best-response (Nash) equilibrium to the class of dynamic games with complete & perfect information.
"dynamic"
takes place over time;
not simultaneous/one-shot
"complete information"
all players know all relevant aspects of the game (especially payoffs)
"perfect information"
all players observe all moves
The Extensive Form
Extensive Form
Nodes:
Branches:
Initial node: where the game begins
Decision nodes: where a player makes a choice; specifies player
Terminal nodes: where the game ends; specifies outcome
Individual actions taken by players; try to use unique names for the same action (e.g. "left") taken at different times in the game
Information sets:
Sets of decision nodes at which the decider and branches are the same, and the decider doesn't know for sure where they are.
A "tree" representation of a game.
Normal-Form vs. Extensive-Form Representations
The extensive-form representation
of a game specifies:
The normal-form representation
of a game specifies:
The strategies available to each player
The player's payoffs for each combination of strategies
The players in the game
When each player moves
The actions available to each player each time it's their move
The players in the game
The player's payoffs for each combination of actions
Strategies and Strategy Spaces
A strategy is a complete, contingent plan of action for a player in a game.
This means that every player
must specify what action to take
at every decision node in the game tree!
A strategy space is the set of all strategies available to a player.
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
Consider the following game.
Player 1 starts.
She chooses X or Y.
Player 2 observes player 1's choice.
If player 1 chose X, player 2 chooses A or B.
If player 1 chose Y, player 2 chooses C or D.
After player 2 makes his choice, the payoffs to each player are realized.
"Play X."
"Play Y."
What is player 1's strategy space?
What is player 2's strategy space?
"Play A after X, and C after Y."
"Play A after X, and D after Y."
"Play B after X, and C after Y."
"Play B after X, and D after Y."
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
X
Y
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
What is player 1's strategy space?
What is player 2's strategy space?
AC
AD
BC
BD
1
2
X
Y
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
AC
AD
BC
BD
We can create the normal-form representation of this game.
3
2
1
0
2
0
1
3
3
2
1
3
2
1
0
0
1
2
X
Y
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
AC
AD
BC
BD
We can create the normal-form representation of this game.
3
2
1
0
2
0
1
3
3
2
1
3
2
1
0
0
What are the Nash equilibria of this normal-form game?
Do any of the Nash equilibria not make sense?
1
2
X
Y
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
AC
AD
BC
BD
3
2
1
0
2
0
1
3
3
2
1
3
2
1
0
0
Think about this: after player 1 makes her move, we are in one of two subgames.
What should player 2 do in each subgame?
1
2
X
Y
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
AC
AD
BC
BD
Think about this: after player 1 makes her move, we are in one of two subgames.
3
2
1
0
2
0
1
3
3
2
1
3
2
1
0
0
What should player 2 do in each subgame?
Anticipating how player 2 will react, therefore, what will player 1 choose?
1
2
X
Y
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
AC
AD
BC
BD
Think about the other Nash equilibrium.
3
2
1
0
2
0
1
3
3
2
1
3
2
1
0
0
This is better for player 2.
It's kind of like player 2 is threatening to play D if player 1 chooses Y.
But this threat is not credible.
Definition: Subgame Perfect Nash Equilibrium
In an extensive-form game of complete and perfect information,
a subgame in consists of a decision node and all subsequent nodes.
A Nash equilibrium is subgame perfect if the players' strategies
constitute a Nash equilibrium in every subgame.
(We call such an equilibrium a Subgame Perfect Nash Equilibrium, or SPNE.)
Informally: a SPNE doesn't involve any non-credible threats or promises.
Another Example: Entry Deterrence
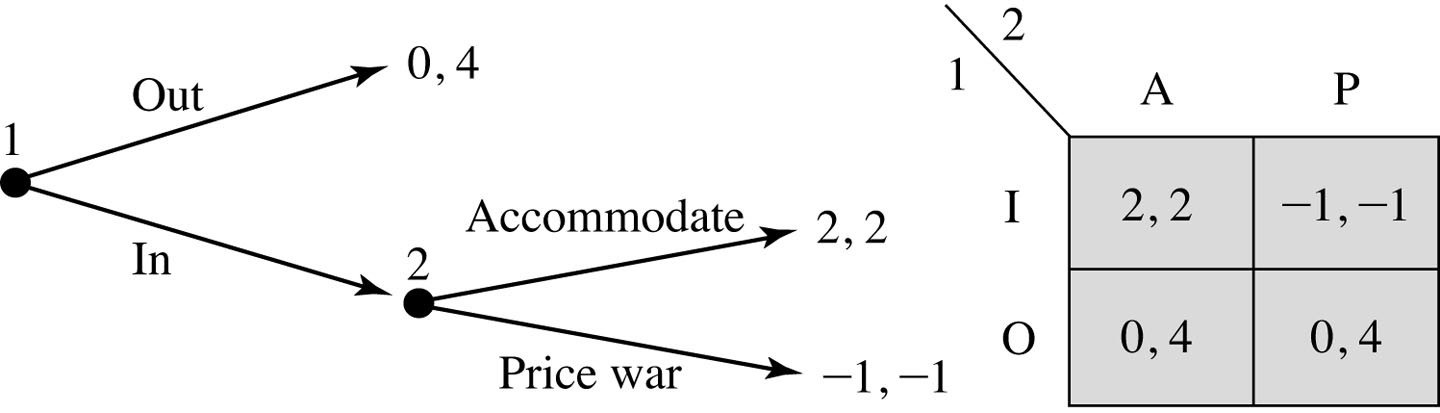
pollev.com/chrismakler
How many subgames does this game have?
What is player 1's
strategy space?
What is player 2's
strategy space?
Backward Induction
The process of starting at the terminal nodes and working backwards to determine what each player will do.
You still have to specify complete, contingent plans of action (i.e. strategies)!
Repeated Games
Key Insight
- In a repeated game, you can sustain behavior which would not be a Nash equilibrium in a one-shot game.
- The mechanism you employ needs to be a credible threat or promise about future behavior.
- "Credible" = cannot involve a strategy which is not subgame perfect: when you get to that point in the game, it has to be an equilibrium from then on
Infinitely Repeated Games
V(\pi_0,\pi_1,\pi_2, \cdots) = \pi_0 + {\pi_1 \over 1 + r} + {\pi_2 \over (1 + r)^2} + \cdots
Recall: when we looked at collusion,
we said a stream of payments had a present value of
This is a special case of a general formulation used in game theory called exponential discounting
V(\pi_0,\pi_1,\pi_2, \cdots) = \pi_0 + \delta \pi_1 + \delta^2 \pi_2 + \cdots
where \(\delta < 1\) is called the "discount factor"
x + {x \over r}
Value of getting payoff \(x\) forever, starting now:
Value of getting payoff \(z\) forever, starting next period:
Value of getting payoff \(y\) now and then payoff \(z\) forever after:
{z \over r}
y + {z \over r}
(for \(\delta = {1 \over 1 + r}\))
{x \over 1 - \delta}
{\delta z \over 1 - \delta}
y + {\delta z \over 1 - \delta}
(for general \(\delta\))
Strategy in an Infinitely Repeated Game
- Must specify what to do in each period,
as a function of all previously taken actions. - We often group action histories to make strategies simpler:
- Grim trigger: "If anyone has ever played 'cheat'"
- Tit-for-tat: "If the other player played 'cheat' last period"
- Limited punishment: "If the other player played 'cheat' in any of the last 3 periods"
Infinitely Repeated Prisoners' Dilemma
1
2
Cooperate
Defect
Cooperate
Defect
2
2
,
3
0
,
1
1
,
0
3
,
Suppose the following prisoner's dilemma is repeated indefinitely,
with future payoffs discounted at rate \(\delta < 1\).
Consider the grim trigger strategy:
If you ever defect, I will defect for all eternity."
For what values of \(\delta\) would that constitute a SPNE?
Finitely Repeated Games
Recall: Coordination
1
2
Top
Bottom
Left
Right
3
1
,
0
0
,
1
3
,
0
0
,
1
2
3
1
,
0
0
,
1
3
,
0
0
,
Top
Middle
Left
Center
Bottom
Right
0
0
,
0
1
,
0
0
,
5
0
,
4
4
,
What are the Nash Equilibria of this game?
Suppose this game is repeated twice,
with no discounting (so payoffs are
just the sum of the two periods).
Can (Bottom, Right) be played in the first period in a SPNE?
Conclusions
- New refinement of Nash equilibrium: subgame perfection
- When you arrive at any node of a game, must be an equilibrium from then on
- Strategies must specify what each player does at every possible node in a game, even if that node is never reached
- In games that take place over time:
- some strategies which are Nash equilibria of the normal-form game are not subgame perfect (involve non-credible threats or promises)
- some strategies which are not Nash equilibria of a simultaneous game may be sustainable if the game is repeated
Econ 51 | 10 | Game Theory II: Dynamic Games
By Chris Makler
