Dynamic Games and Subgame Perfection
Christopher Makler
Stanford University Department of Economics
Econ 51: Lecture 10
Golden Balls
Split
Split
1
2
Steal
Steal
1
1
2
0
0
2
0
0
Golden Balls
Split
Split
1
2
Steal
Steal
1
1
2
0
0
2
0
0
Big Ideas
Credibility: can you credibly threaten some retaliation, or promise
some reward, to get the other player to do something you want?
Finite vs. Infinite Time Horizon: Does the game end?
Subgames: games will have more than one move; we can break them
up and examine subgames which are like games-within-games.
What's wrong with Nash Equilibrium?
Today's Agenda
Part 1: Discrete Strategies
Part 2: Continuous Strategies
Review: Extensive Form Games
Backward Induction
Strategies in Extensive Form Games
Subgame Perfect Nash Equilibrium
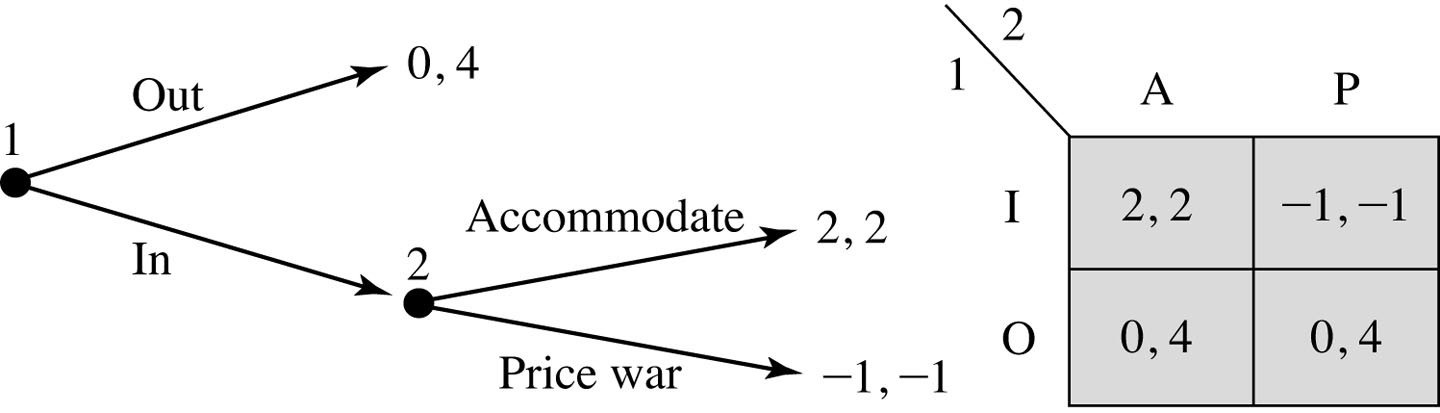
Example: Entry Deterrence
Example: Ultimatum Game
Example: Stackelberg Duopoly
Review: Extensive Form Games
Normal-Form vs. Extensive-Form Representations
The extensive-form representation
of a game specifies:
The normal-form representation
of a game specifies:
The strategies available to each player
The player's payoffs for each combination of strategies
The players in the game
When each player moves
The actions available to each player each time it's their move
The players in the game
The player's payoffs for each combination of actions
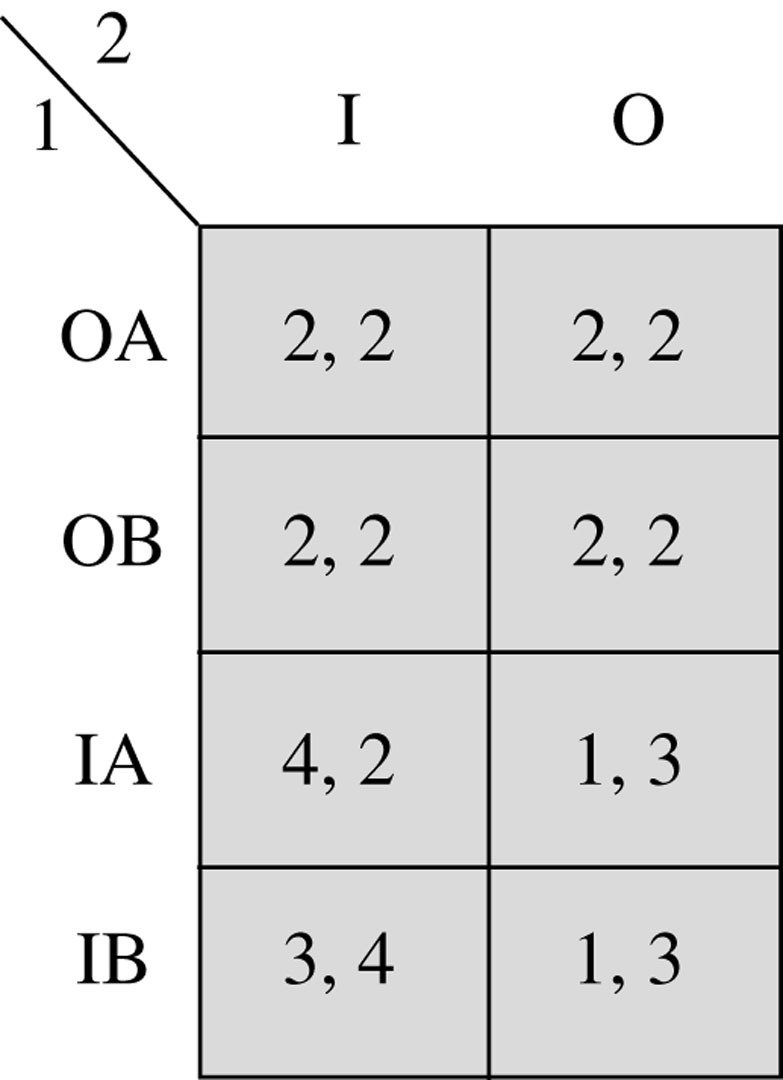
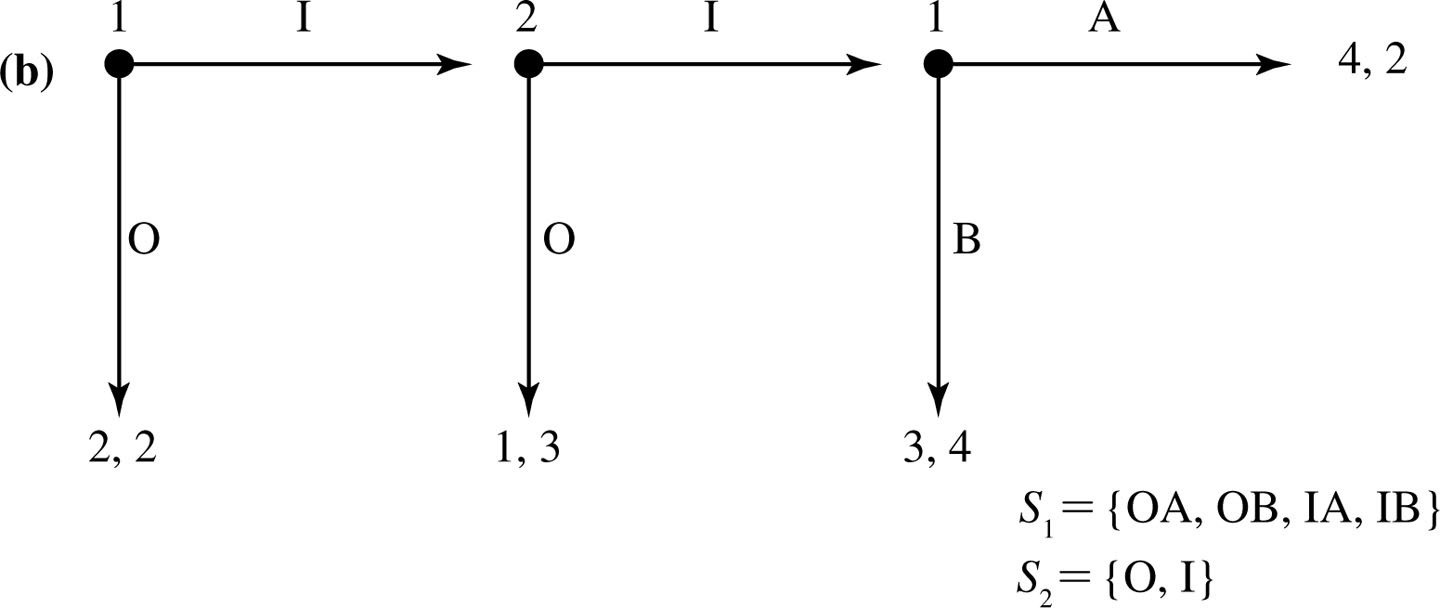
Circle the best responses. What's wrong?
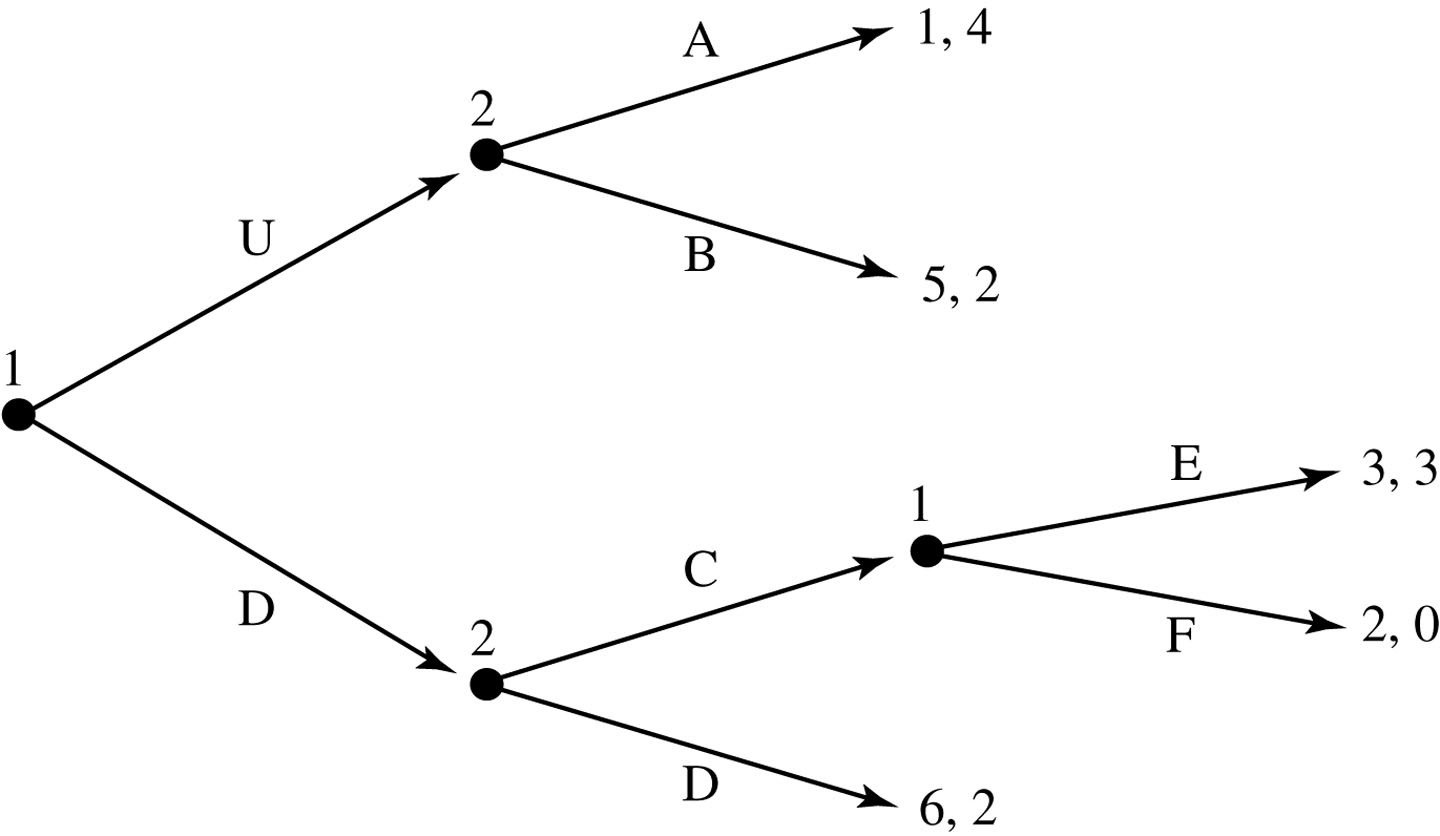
One way to solve this game: backwards induction.
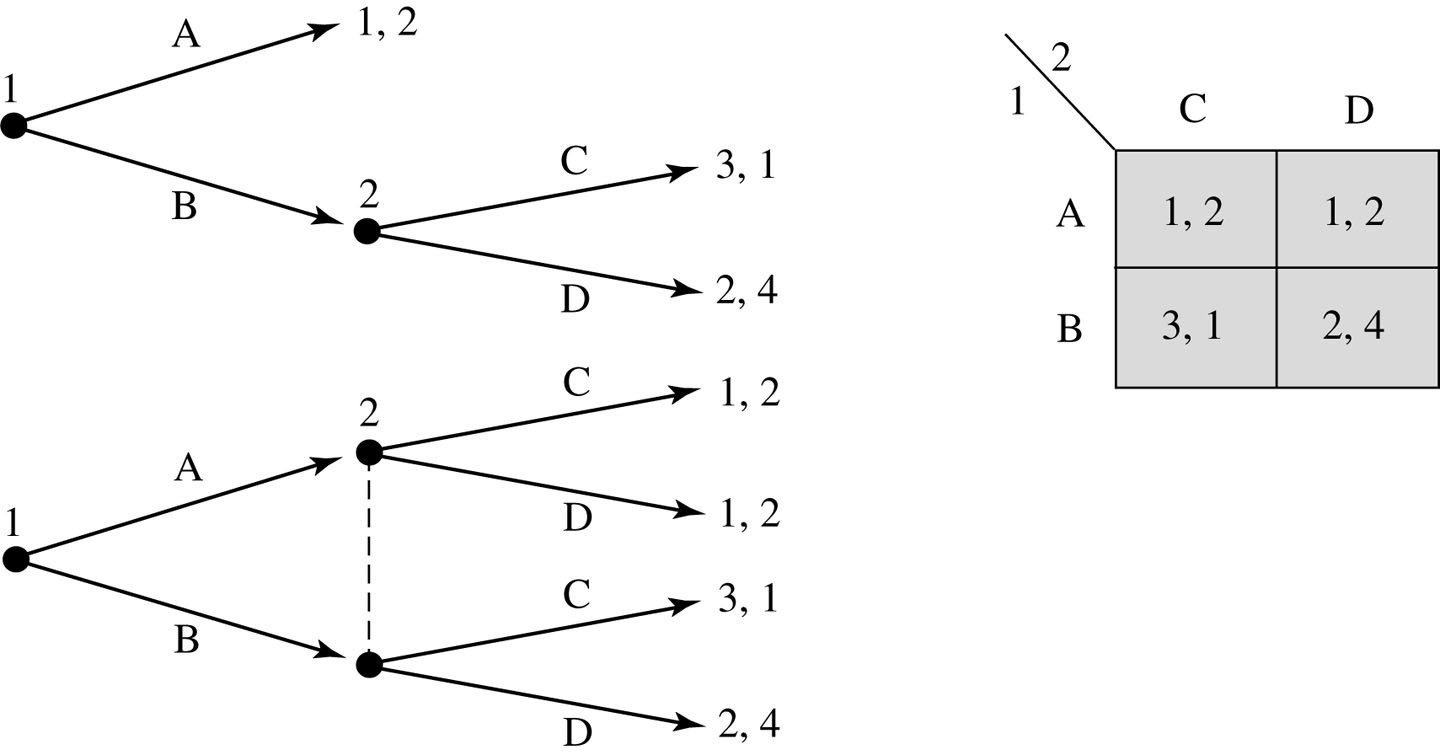
Backwards induction is a method of determining the outcome(s) of a game by starting at the end and working backwards.
Finite games: start from terminal nodes
Infinite games: a bit more complicated
Subgame Perfect Nash Equilibrium
1
2
X
Y
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
Create the normal-form representation of this game. What are the Nash Equilibria?
Definition: Subgame Perfect Nash Equilibrium
In an extensive-form game of complete and perfect information,
a subgame in consists of a decision node and all subsequent nodes.
A Nash equilibrium is subgame perfect if the players' strategies
constitute a Nash equilibrium in every subgame.
(We call such an equilibrium a Subgame Perfect Nash Equilibrium, or SPNE.)
Informally: a SPNE doesn't involve any non-credible threats or promises.
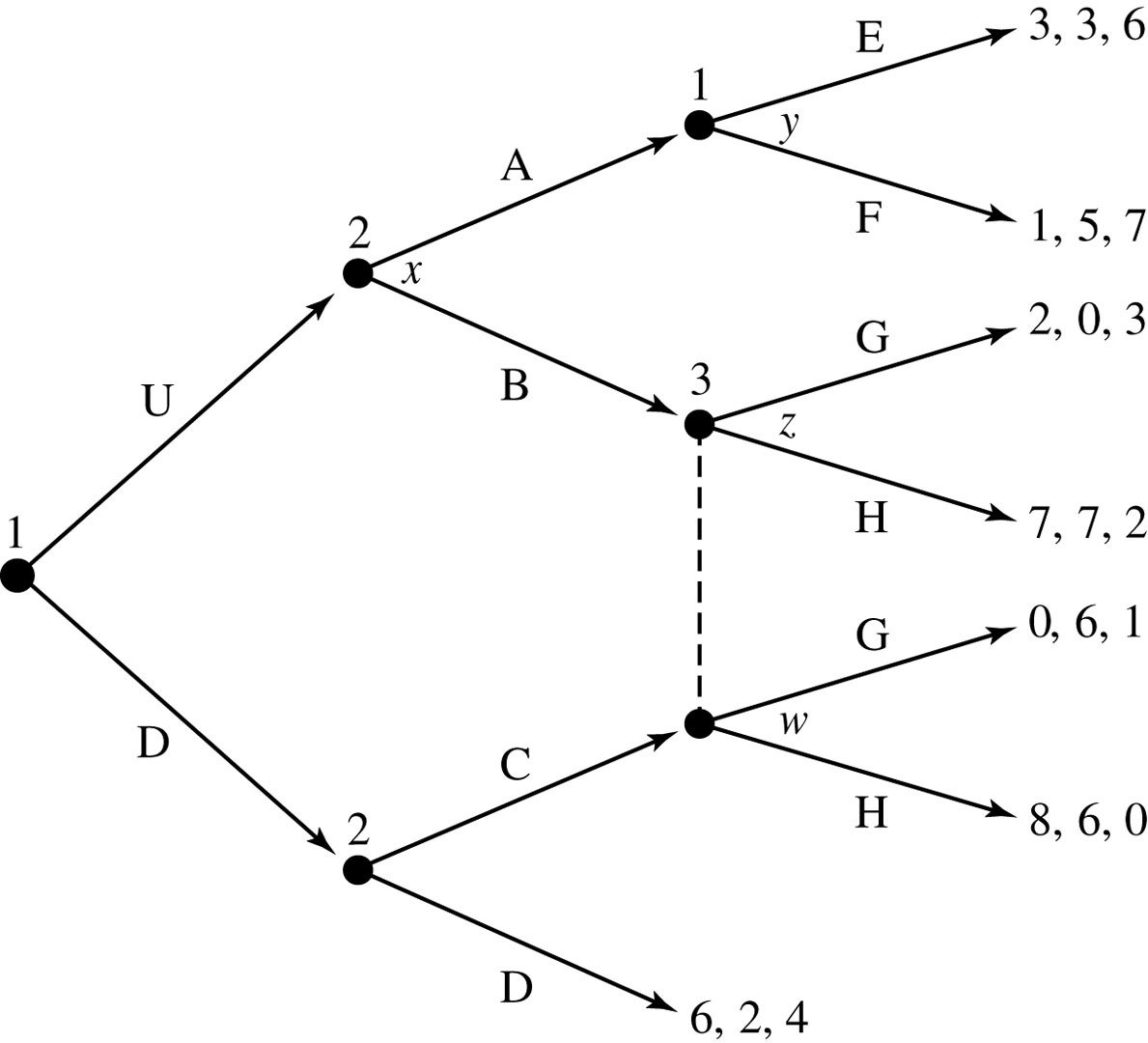
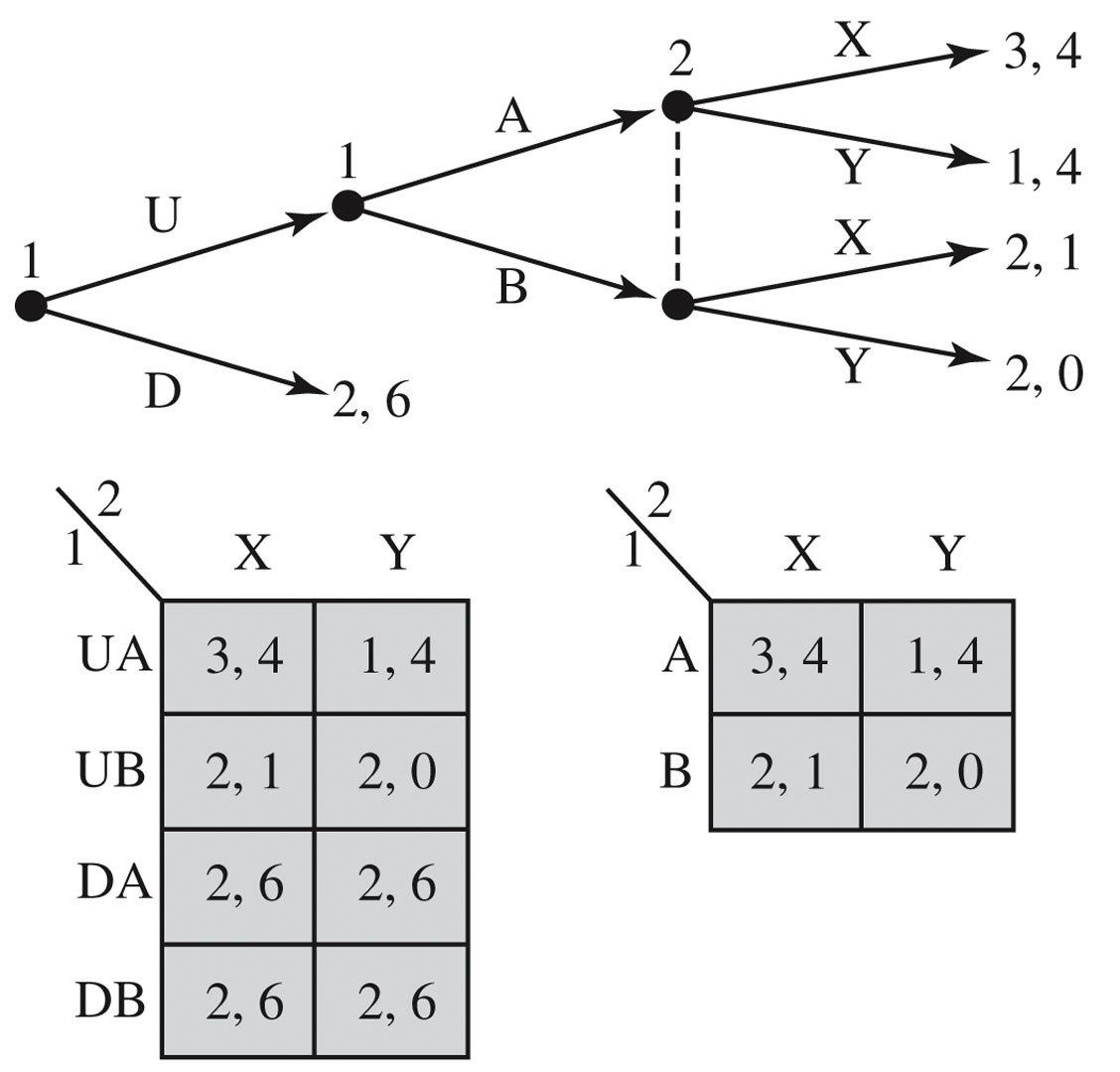
A Subgame Perfect Nash Equilibrium must specify a NE in every subgame!
Continuous Strategies
How do we represent a continuous strategy in an extensive-form game?
(For example, the quantity chosen by a firm in a Cournot-like game?)
Player 1: Offers a split of $100 to player 2.
Player 2: Accepts or rejects the offer:
if accepts, split as player 1 said
if rejects, nobody gets any
Example: Ultimatum Game
Players: Two firms, Firm 1 and Firm 2
Payoffs:
Market price is determined by total output produced
Profit to Firm 2:
\pi_2(q_1,q_2) = P(q_1,q_2)q_2 - c_2(q_2)
Profit to Firm 1:
\pi_1(q_1,q_2) = P(q_1,q_2)q_1 - c_1(q_1)
P(q_1,q_2) = 14 - (q_1 + q_2)
c_1(q_1) = 2q_1
c_2(q_2) = 2q_2
\text{Market Demand: }
\text{Firm 1's Costs: }
\text{Firm 2's Costs: }
New twist:
Firm 1 chooses \(q_1\) first;
Firm 2 observes \(q_1\) and chooses \(q_2\)
What are the strategy spaces?
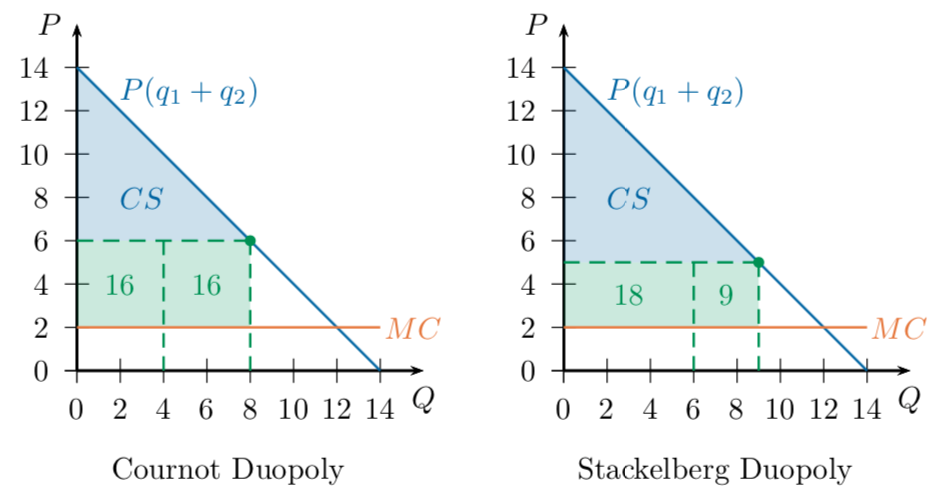
Example: Stackelberg Duopoly
Profit to Firm 2:
\pi_2(q_1,q_2) = P(q_1,q_2)q_2 - c_2(q_2)
Profit to Firm 1:
\pi_1(q_1,q_2) = P(q_1,q_2)q_1 - c_1(q_1)
P(q_1,q_2) = 14 - (q_1 + q_2)
c_1(q_1) = 2q_1
c_2(q_2) = 2q_2
\text{Market Demand: }
\text{Firm 1's Costs: }
\text{Firm 2's Costs: }
Comparing Outcomes
P = 8, Q = 6
CS = 32
\pi_1 = \pi_2 = 16
P = 5, Q = 9
CS = 40.5
\pi_1 = 18, \pi_2 = 9
Econ 51 | Spring 22 | Dynamic Games and Subgame Perfection
By Chris Makler
Econ 51 | Spring 22 | Dynamic Games and Subgame Perfection
Sequential and Repeated Games of Perfect Information
