Signaling and Lemons
To navigate: press "N" to move forward and "P" to move back.
To see an outline, press "ESC". Topics are arranged in columns.
Today's Agenda
Part 1: Job Market Signaling
Part 2: The Market for "Lemons"
Big Idea
One agent has information about the game that the other agent lacks.
The central problem here is how to credibly signal information;
absent that ability, there can be an adverse selection problem.
Job Market Signaling
Job Market Signaling (Spence, 1973)
There are two types of workers: "high-ability" and "low-ability."
High-ability workers
are worth \(y_H\) to a firm
Low-ability workers
are worth \(y_L\) to a firm
Assume both firms and high-ability workers would be better off if firms could observe their ability.
Need some mechanism to create a separating equilibrium.

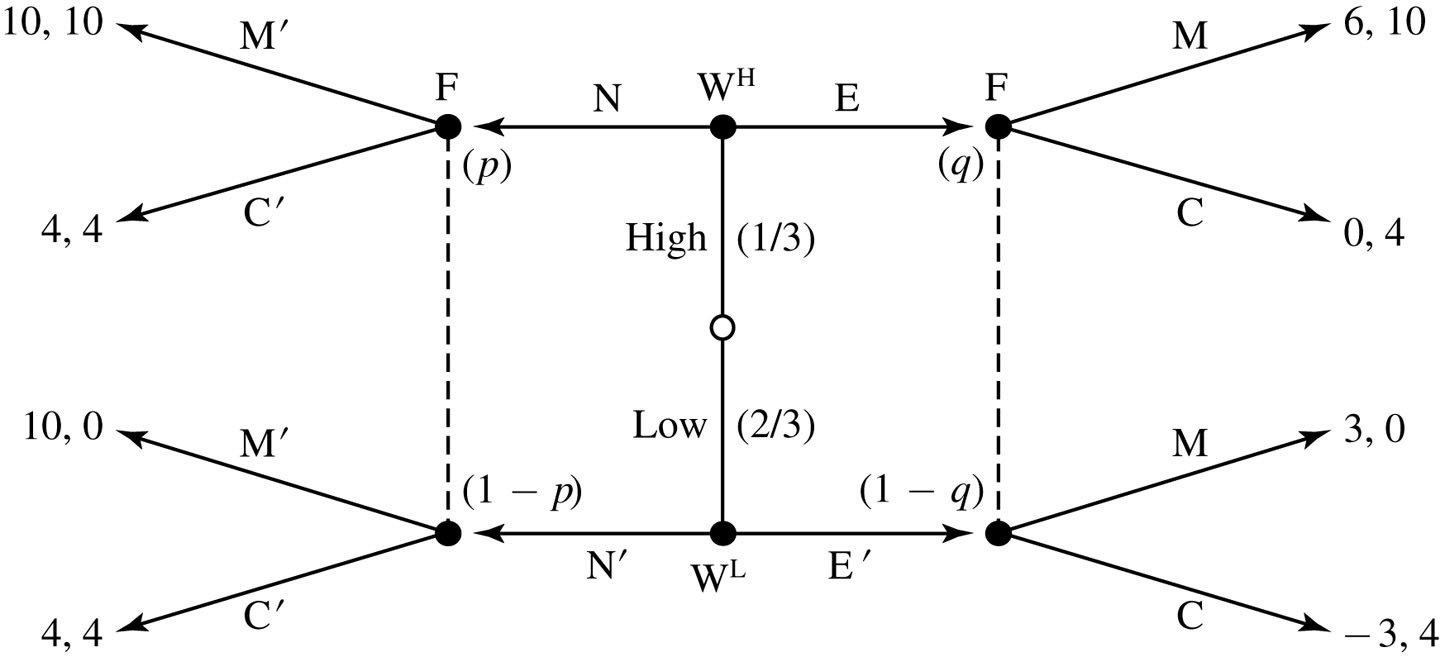
Workers are of two types: 1/3 are high ability and 2/3 are low ability.
They can choose to get an education (E) or not (N)
The high type incurs a cost of education of 4; the low type incurs a cost of 7.
Firms observe the education -- but not the type of the worker
-- and choose to put them into a management job or a clerical job.
A high-ability worker in a management job is worth 10 to the firm;
a low-ability worker in a management job is worth 0 to the firm.
Either type is worth 4 in a clerical job.
The management job is worth 10 to either type of worker;
a clerical job is worth 4 to either type of worker.
Is there a separating equilibrium?
Is there a pooling equilibrium?
The Market for Lemons
The Market for Lemons (Akerlof, QJE 1970)
There are two types of used cars: "lemons" and "plums."
Assume there are equal numbers of each car.
"Plums" are worth
$2000 to a seller
and $2400 to a buyer.
"Lemons" are worth
$1000 to a seller
and $1200 to a buyer.
If the quality of a car is observable to a buyer, what will happen?
If the quality of a car is not observable to a buyer, and all cars are on the market, what is the expected value to a buyer from buying a random car?
If that is the most buyers are willing to spend, which cars will be offered for sale?
Both types will be sold.
$1800
Only lemons!


How can we solve this problem?
Convert to a separating equilibrium in which sellers
credibly reveal the type of car they're selling.
Suppose the seller could pay $100 to get their car quality certified.
Assume that if the car is certified, it's sold for $50 less than the buyer value: \(p_P = 2350, p_L = 1150\). If a car isn't certified, its price is \(p\).
(buyer pays $2350; seller gets $2250)
(buyer pays $p;
seller gets $p)
(buyer pays $1150; seller gets $1050)
(buyer pays $p;
seller gets $p)
Could \(p\) be high enough to get sellers of plums to not certify their cars?
No.
Is it ever worth it for sellers of lemons to certify their cars?
No.

The market for lemons: separating equilibria
Without certification possibility
With $100 certification
Sellers of plums don't put their cars on the market; sellers of lemons do.
Buyers believe any car for sale is a lemon
Price of any car is $1150;
only lemons sell.
Sellers of plums pay to get their car certified; sellers of lemons don't.
Buyers believe any car that isn't certified is a lemon.
Price of a certified-plum car is $2150, price of a lemon is $1150. All cars sell.
Copy of Econ 51 | 17 | Signaling and Lemons
By Chris Makler
Copy of Econ 51 | 17 | Signaling and Lemons
Signaling and Lemons
- 696



