Production and Cost in the Short Run
To navigate: press "N" to move forward and "P" to move back.
To see an outline, press "ESC". Topics are arranged in columns.
Today's Agenda
Part 1: Total and Unit Cost Curves
Part 2: Relationship of Production to Cost
Expansion paths and total cost in the SR
Fixed and variable costs
Average costs
Marginal cost
Relationship between Average & Marginal
Production and Cost with One Input
Returns to Scale with Two Inputs
Economies and Diseconomies of scale
Producer Theory
L∗(w,r,y)
L^*(w,r,y)
K∗(w,r,y)
K^*(w,r,y)
Exogenous Variables
Endogenous Variables
technology, f()
level of output, y
factors used
total cost, c(y)
Cost Minimization
Production Set
Choice
Rule
factor prices (w, r)
y∗(w,r,p)
y^*(w,r,p)
optimal level of output, y*
Profit Maximization
output prices
Total Revenue R(y)
Total Cost, c(y)
Last Time
Today
Wednesday
Example
f(L,K)=L41K41
f(L,K) = L^\frac{1}{4}K^\frac{1}{4}
We found before that
L∗(y)=wry2
L^*(y) = \sqrt{\frac{r}{w}}y^2
K∗(y)=rwy2
K^*(y) = \sqrt{\frac{w}{r}}y^2
c(y)=wL∗(y)+rK∗(y)
c(y) = wL^*(y) + rK^*(y)
=wwry2+rrwy2
=w\sqrt{\frac{r}{w}}y^2 + r\sqrt{\frac{w}{r}}y^2
=2wry2
=2\sqrt{wr}y^2
=wry2+wry2
=\sqrt{wr}y^2 + \sqrt{wr}y^2
The Firm in the Short Run
In the "short run" at least one input is fixed.
We'll use the metaphor that that input is capital (K).
Short-Run Costs
L∗(w∣y,K)
L^*(w|y,\overline{K})
Exogenous Variables
Endogenous Variables
technology, f()
level of output, y
fixed inputs
prices of variable inputs
Optimal Choice of Inputs
Production Set
Choice
Rule
cs(y∣K,w)
c_s(y|\overline{K},w)
FOR VARIABLE INPUT(S)
COST FUNCTION
CONDITIONAL DEMAND
Simplifying Assumption: If there are only two inputs,
there there's no "optimal choice" to be made:
there's only one choice of labor if y and capital are both fixed.
Conditional Demand
in the Short Run
If there's only one variable input,
it's perfectly inelastic -- there's only one choice!
Our continuing example
f(L,K)=L41K41
f(L,K) = L^\frac{1}{4}K^\frac{1}{4}
If K is fixed at K, then
L∗(y)=Ky4
L^*(y) = \frac{y^4}{\overline K}
y=L41K41
y = L^\frac{1}{4}\overline K^\frac{1}{4}
Solve for L to get
pollev.com/chrismakler
Short-Run Total Cost of y Units
cs(y,K)=wL(y,K)+rK
c_s(y,\overline{K}) = wL(y,\overline{K}) + r\overline{K}
Variable cost
"The total cost of producing y units in the short run
is the variable cost of the required amount of the input that can be varied,
plus the fixed cost of the input that is fixed in the short run."
Fixed cost
Rejoining our friend
f(L,K)=L41K41
f(L,K) = L^\frac{1}{4}K^\frac{1}{4}
We found before that
c(y)=wL∗(y)+rK
c(y) = wL^*(y) + r\overline K
L∗(y)=Ky4
L^*(y) = \frac{y^4}{\overline K}
c(y)=Kwy4+rK
c(y) = \frac{wy^4}{\overline K} + r\overline K
Therefore SR total costs are
pollev.com/chrismakler
Relationship between
Short-Run and Long-Run Costs
cs(y,K)=Cost if capital is fixed at K
c_s(y,\overline{K}) = \text{Cost if capital is fixed at }\overline{K}
cs(y,K∗(y))=Cost if capital is fixed at optimal K for producing y
c_s(y,K^*(y)) = \text{Cost if capital is fixed at optimal }K \text{ for producing }y
What conclusions can we draw from this?
cs(y,K)≥c(y)
c_s(y,\overline{K}) \ge c(y)
=c(y) – i.e., the long-run total cost of y
= c(y) \text{ -- i.e., the long-run total cost of }y
c(y) is the lower envelope of the family of cs(y) curves
c(y) \text{ is the lower envelope of the family of }c_s(y)\text{ curves}
Ongoing Mathematical Example: f(L,K)=L41K41
\text{Ongoing Mathematical Example: }f(L,K) = L^\frac{1}{4} K^\frac{1}{4}
c(w,r,y)=2wry2
c(w,r,y) = 2\sqrt{wr}y^2
cs(w,r,y)=wKy4+rK
c_s(w,r,y) = w\frac{y^4}{\overline{K}} + r\overline{K}
Long-run and Short-Run Total Cost Functions:
\text{Long-run and Short-Run Total Cost Functions: }
Now let’s fix w=r=10 and K=25:
\text{Now let's fix }w=r=10\text{ and }\overline K = 25:
c(y)=20y2
c(y) = 20y^2
cs(y)=250+0.4y4
c_s(y) = 250+0.4y^4
LONG RUN
SHORT RUN
Fixed and Variable Costs
Fixed and Variable costs
cs(y,K)=wL(y,K)+rK
c_s(y,\overline{K}) = wL(y,\overline{K}) + r\overline{K}
Cost of variable inputs
Cost of fixed inputs
c(y)=cv(y)+F
c(y) = c_v(y) + F
From input decision ("Cost Minimization" chapter):
When thinking about output ("Cost Curves" chapter):
Fixed Costs (F): All economic costs that don't vary with output.
Variable Costs (VC): All economic costs that vary with output
Opp. costs, sunk costs, "quasi-fixed" costs
Ongoing Mathematical Example: f(L,K)=L41K41
\text{Ongoing Mathematical Example: }f(L,K) = L^\frac{1}{4} K^\frac{1}{4}
c(y)=20y2
c(y) = 20y^2
cs(y)=250+0.4y4
c_s(y) = 250+0.4y^4
LONG RUN
SHORT RUN
F
F
cv(y)
c_v(y)
Average Costs
Total Cost (TC):c(y)=cv(y)+F
\text{Total Cost (TC)}: c(y) = c_v(y) + F
Average Cost (AC):yc(y)=ycv(y)+yF
\text{Average Cost (AC)}: \frac{c(y)}{y} = \frac{c_v(y)}{y} + \frac{F}{y}
Fixed Costs (F)
Variable Costs (VC)
Average Fixed Costs (AFC)
Average Variable Costs (VC)
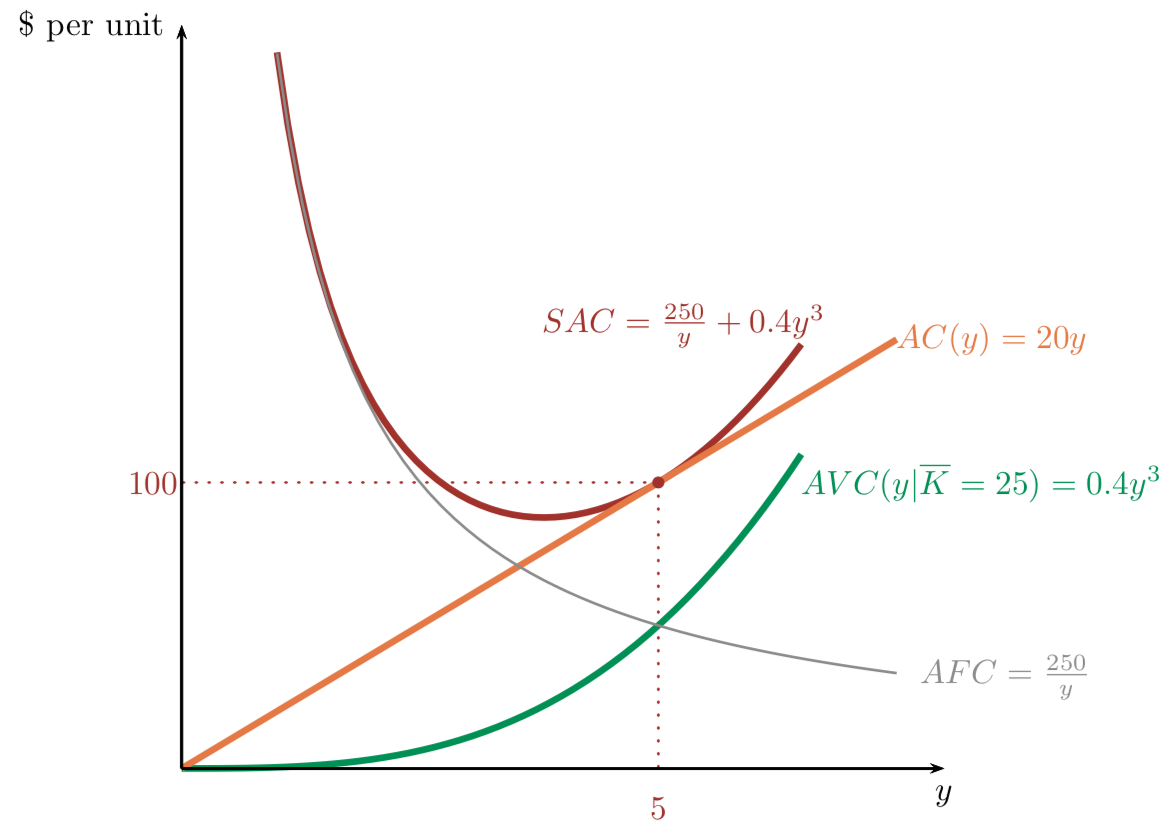
Average fixed, variable, and total costs
Ongoing Mathematical Example: f(L,K)=L41K41
\text{Ongoing Mathematical Example: }f(L,K) = L^\frac{1}{4} K^\frac{1}{4}
c(y)=20y2
c(y) = 20y^2
cs(y)=250+0.4y4
c_s(y) = 250+0.4y^4
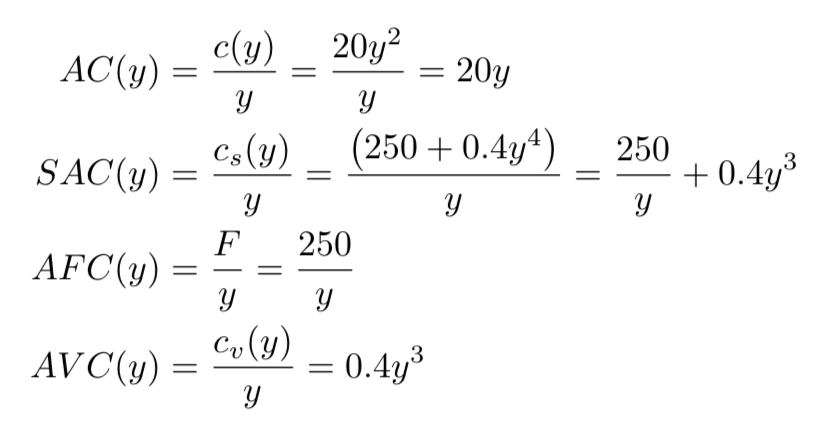
LONG RUN
SHORT RUN
Comparing Total and Average Costs
Fixed costs are constant;
average fixed costs start at infinity and decrease
Variable costs start from zero and increase;
so do average variable costs.
Short-run total costs start at F and increase by VC;
SAC start out like AFC (since AVC = 0)
and end up like AVC (as AFC approaches 0).
Long-run total costs start from zero and increase;
so do long-run average total costs. This is because we're assuming there are no other fixed costs (e.g. opp. costs)
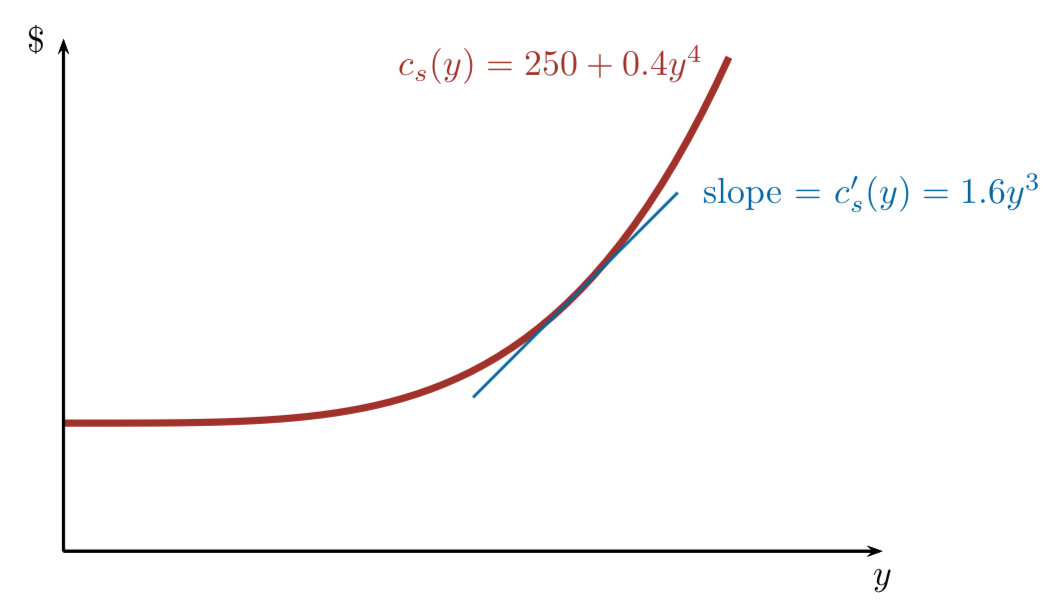
Marginal Costs
Total Cost (TC):c(y)=cv(y)+F
\text{Total Cost (TC)}: c(y) = c_v(y) + F
Marginal Cost (MC):c′(y)=cv′(y)+0
\text{Marginal Cost (MC)}: c'(y) = c_v'(y) + 0
Fixed Costs (F)
Variable Costs (VC)
(Marginal cost = marginal variable cost)
Ongoing Mathematical Example: f(L,K)=L41K41
\text{Ongoing Mathematical Example: }f(L,K) = L^\frac{1}{4} K^\frac{1}{4}
c(y)=20y2
c(y) = 20y^2
cs(y)=250+0.4y4
c_s(y) = 250+0.4y^4
LONG RUN
SHORT RUN
LMC(y)=c′(y)=40y
LMC(y) = c'(y) = 40y
SMC(y)=cs′(y)=1.6y3
SMC(y) = c'_s(y) = 1.6y^3
pollev.com/chrismakler
Relationship between Average and Marginal Costs
Marginal cost tends to "pull" average cost toward it:
MC>AC⇒AC increasing
MC > AC \Rightarrow AC \text{ increasing}
MC=AC⇒AC constant
MC = AC \Rightarrow AC \text{ constant}
MC<AC⇒AC decreasing
MC < AC \Rightarrow AC \text{ decreasing}
Marginal grade = grade on last test, average grade = GPA
Ongoing Mathematical Example: f(L,K)=L41K41
\text{Ongoing Mathematical Example: }f(L,K) = L^\frac{1}{4} K^\frac{1}{4}
cs(y)=250+0.4y4
c_s(y) = 250+0.4y^4
SHORT RUN
SMC(y)=cs′(y)=1.6y3
SMC(y) = c'_s(y) = 1.6y^3
SAC(y)=ycs(y)=y250+0.4y3
SAC(y) = \frac{c_s(y)}{y} = \frac{250}{y} + 0.4y^3
Production and Cost with One Input
The Curvature of the Production Function affects the Curvature of the Total Cost Curve.
Decreasing marginal returns => increasing marginal cost
Constant marginal returns => constant marginal cost
Increasing marginal returns => decreasing marginal cost
How does this work with more than one input?
Think returns to scale.
Returns to a Single Input
- Increasing marginal product: MPL is increasing in L
- Constant marginal product: MPL is constant in L
- Diminishing marginal product: MPL is decreasing in L
Returns to Scale (Scaling all inputs.)
- Increasing returns to scale: doubling all inputs more than doubles output.
- Constant returns to scale: doubling all inputs exactly doubles output.
- Decreasing returns to scale: doubling all inputs less than doubles output.
How do the attributes of the production function
(diminishing marginal product, returns to scale)
affect average costs?
Intuitively: if you have diminishing productivity, you'll have increasing marginal costs and eventually increasing average costs.
Relationship between Production Function and the Curvature of Long-Run and Short-Run Costs
- If the production function has diminishing MPL, the short-run cost curve will get steeper as you produce more output (have increasing marginal costs)
- If the production function has decreasing returns to scale, the long-run cost curve will get steeper as you produce more output.
- What about for constant returns to scale? Increasing returns to scale?
Economies and Diseconomies of Scale
Returns to Scale
Has to do with the production function
Economies of Scale
Has to do with cost curves
Increasing Returns to Scale:
double input => more than double output
Decreasing Returns to Scale:
double input => less than double output
Always deals with the long run
Can occur in both the long run and short run
Economies of Scale:
increasing output lowers average costs
Diseconomies of Scale:
increasing output raises average costs
In the short run, the cost of producing y units of output is the sum of the variable cost wL(y) and the fixed cost rK.
Unit costs (average costs and marginal costs) are direct derivations from the total cost functions.
The curvature of cost curves is related to the nature of the production function: diseconomies of scale and rising marginal costs come from diminishing marginal returns to inputs.
Conclusion and Next Steps
Next: profit maximization, output supply, and input demands for competitive firms.
Production and Cost in the Short Run To navigate: press "N" to move forward and "P" to move back. To see an outline, press "ESC". Topics are arranged in columns.
Econ 50 | Production and Cost in the Short Run
By Chris Makler
Econ 50 | Production and Cost in the Short Run
Having derived the total cost of producing y units in the short run and long run, we take a closer look at total cost (fixed and variable) and unit cost curves (average and marginal). We then examine the relationship between the nature of production processes and their associated cost curves.
- 1,481
