Information and the Principal-Agent Model
To navigate: press "N" to move forward and "P" to move back.
To see an outline, press "ESC". Topics are arranged in columns.
Today's Agenda
Part 1: Discrete Strategies
Part 2: The Principal-Agent Model
Unit Motivation: Mechanism Design
Incomplete Information: Role of "Nature"
Evaluating Probabilistic Payoffs
Bayesian Normal Form
Baseline: Observable Effort
Unobservable Effort
Continuous Effort Choice
Big Idea
Everything we've done in Econ 50 and 51 has been talking about how
individual agents behave, taking the mechanism of their interactions as given.
For the rest of the course we will endogenize the mechanism:
what if one of the agents sets the rules of the game?
Mechanism Design
Game
Players
Strategies
Payoffs
Mechanism
Players with Hidden Information
Actions
Outcomes
Given this game,
what outcome do we predict will happen?
Given a desired outcome,
what game can we design to achieve it?
"Reverse Game Theory"
The designer is interested in the outcome
but lacks complete information
Selling train tickets to people with different valuations
Auctioning off a painting to people with different (private) valuations
Splitting rent / choosing rooms in an apartment
Hiring an employee/contractor whose effort you can't observe
Selling a car whose type (quality) isn't observable
Fundamental Questions
If people have hidden information,
(there's an adverse selection problem)
what mechanism can a designer establish
to get them to reveal that information?
If people can take hidden actions,
(there's a moral hazard problem)
what mechanism can a designer establish
to get them to choose the action the designer wants them to take?
Incomplete Information and the Role of “Nature"
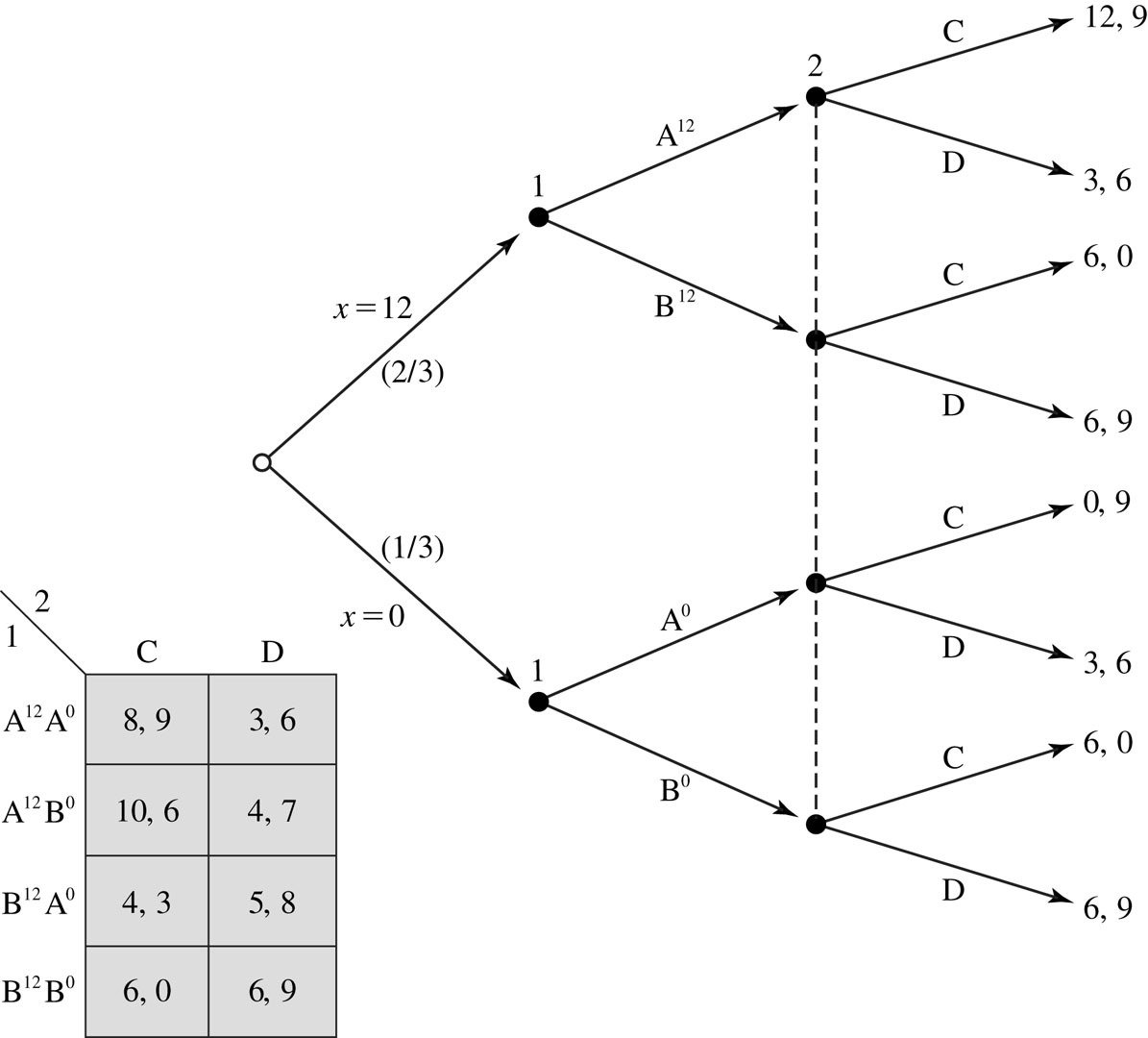
Example
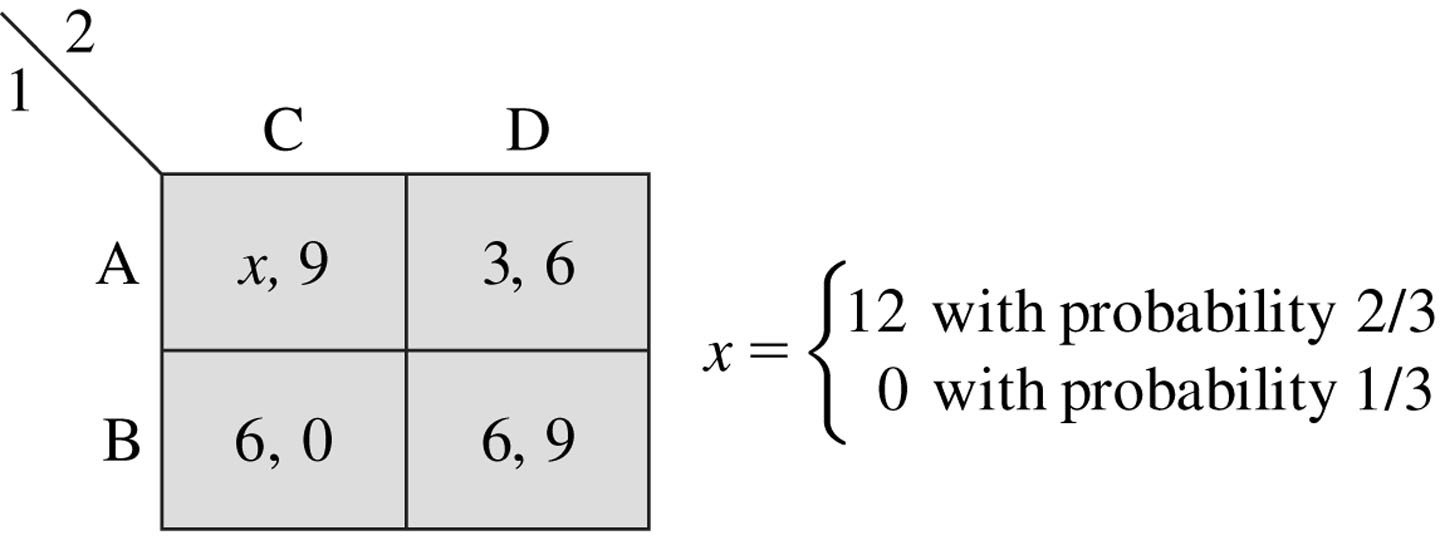
Consider the following game:
Player 1 knows the value of \(x\).
Player 2 knows that \(x\) is 12 with probability \(\frac{2}{3}\)
and 0 with probability \(\frac{1}{3}\)
Principal-Agent Model
Principal: Someone who needs someone else to do something
Agent: The person who needs to do the thing
CEO / sales rep
Professor / student
Landowner / farmer
The principal's payoff depends on the actions of the agent
Can they incentivize the agent to do what they want?
The principal is an employer. The agent is a sales rep.
The agent can choose to put in effort or to shirk.
If they put in effort, they'll make a sale with 80% probability.
If they shirk, they'll make a sale with 50% probability.
Putting in effort costs the agent \(c\).
The principal cannot observe the amount of effort,
but can only observe whether the sale was made (payoff \(r_H\)) or not (payoff \(r_L\)).
Approach: set a base salary \(S\) plus a bonus \(B\) if a sale is made.
\(S - c\) , \(r_L - S\)
Nature
0.2
0.8
Principal
Principal
No sale
Sale
Nature
No sale
Sale
Agent
Effort
Shirk
0.5
0.5
\(S\) ,
\(r_L - S\)
\(S + B - c\) , \(r_H - S - B\)
\(S + B\) , \(r_H - S - B\)
Incentive compatibility constraint:
Bonus must be enough to encourage effort.
Participation constraint:
Value of the contract must be better than outside options.
Example (Burkey Academy Video)
If project is successful, worth \(Q_H = 400\) to principal;
if unsuccessful, worth \(Q_L = 100\).
If agent exerts effort \((c = 1)\), project is successful w/prob \(p_E = \frac{2}{3}\);
if not \((c = 0)\), successful with probability \(p_N = \frac{1}{3}\)
Agent can reject the deal and get \(\underline u = 10\)
Payoffs
U_p(Q,w) = Q - w
U_a(w,c) = \sqrt{w} - c
Principal chooses a wage structure \(w\)
Example (Burkey Academy Video)
If project is successful, worth \(Q_H = 400\) to principal;
if unsuccessful, worth \(Q_L = 100\).
If agent exerts effort \((c = 1)\), project is successful w/prob \(p_E = \frac{2}{3}\);
if not \((c = 0)\), successful with probability \(p_N = \frac{1}{3}\)
Agent can reject the deal and get \(\underline u = 10\)
Payoffs
U_p(Q,w) = Q - w
U_a(w,c) = \sqrt{w} - c
Principal chooses a wage structure \(w\)
Baseline Model: Observable Effort
Contract specifies an effort level and a wage as long as that effort is given (and zero otherwise).
What wage would the principal set?
What would their expected payoff be?
| Principal | Agent | |
|---|---|---|
| Effort | ||
| No Effort | ||
| Reject |
Example (Burkey Academy Video)
If project is successful, worth \(Q_H = 400\) to principal;
if unsuccessful, worth \(Q_L = 100\).
If agent exerts effort \((c = 1)\), project is successful w/prob \(p_E = \frac{2}{3}\);
if not \((c = 0)\), successful with probability \(p_N = \frac{1}{3}\)
Agent can reject the deal and get \(\underline u = 10\)
Payoffs
U_p(Q,w) = Q - w
U_a(w,c) = \sqrt{w} - c
Principal chooses a wage structure \(w\)
Hidden Effort
Wage structure depends on success:
\(w_H\) if project successful, \(w_L\) if not.
What\((w_H,w_L)\) encourages high effort (incentive compatible) and no rejection (participation)?
| Principal | Agent | |
|---|---|---|
| Effort | ||
| No Effort | ||
| Reject |
Continuous Effort Choice
Project pays \(y = 6\) if unsuccessful, \(y = 18\) if successful.
As usual, the principal can set wage based on success, but not effort.
Probability of success = effort of agent: Pr{18} = e, Pr{6} = 1 - e
Suppose the agent can choose a level of effort e, between 0 and 1.
Cost of effort is \(c(e) = 8e^2\). Both are risk neutral, so their payoffs are
U_a(e)=\mathbb{E}[w|e]-c(e)
=ew_H + (1-e)w_L -8e^2
Finally, the agent has an outside option which pays them \(\underline u = 6.5\).
What is the profit-maximizing contract for the principal?
How much effort will the agent put in as a function of \(w_H\) and \(w_L\)?
(bear in mind that they can reject the contract as well)
U_p(e)=\mathbb{E}[(y-w)|e]
=e(18 - w_H) + (1-e)(6 - w_L)
Conclusions and Next Steps
Today we introduced two new concepts: a mechanism and asymmetric information.
Next time, we introduce strategic interaction
by looking at the mechanism of an auction
and the equilibrium strategies of bidders.
A contract is one example of a mechanism
which can encourage high effort
even when effort is unobservable.
Econ 51 | 19 | Principal-Agent Problem
By Chris Makler
Econ 51 | 19 | Principal-Agent Problem
Random events, incomplete information, and the principal-agent problem
