Computing Bottom SCCs Symbolically Using Transition Guided Reduction

Nikola Beneš, Luboš Brim, Samuel Pastva, and David Šafránek

bottom strongly connected components

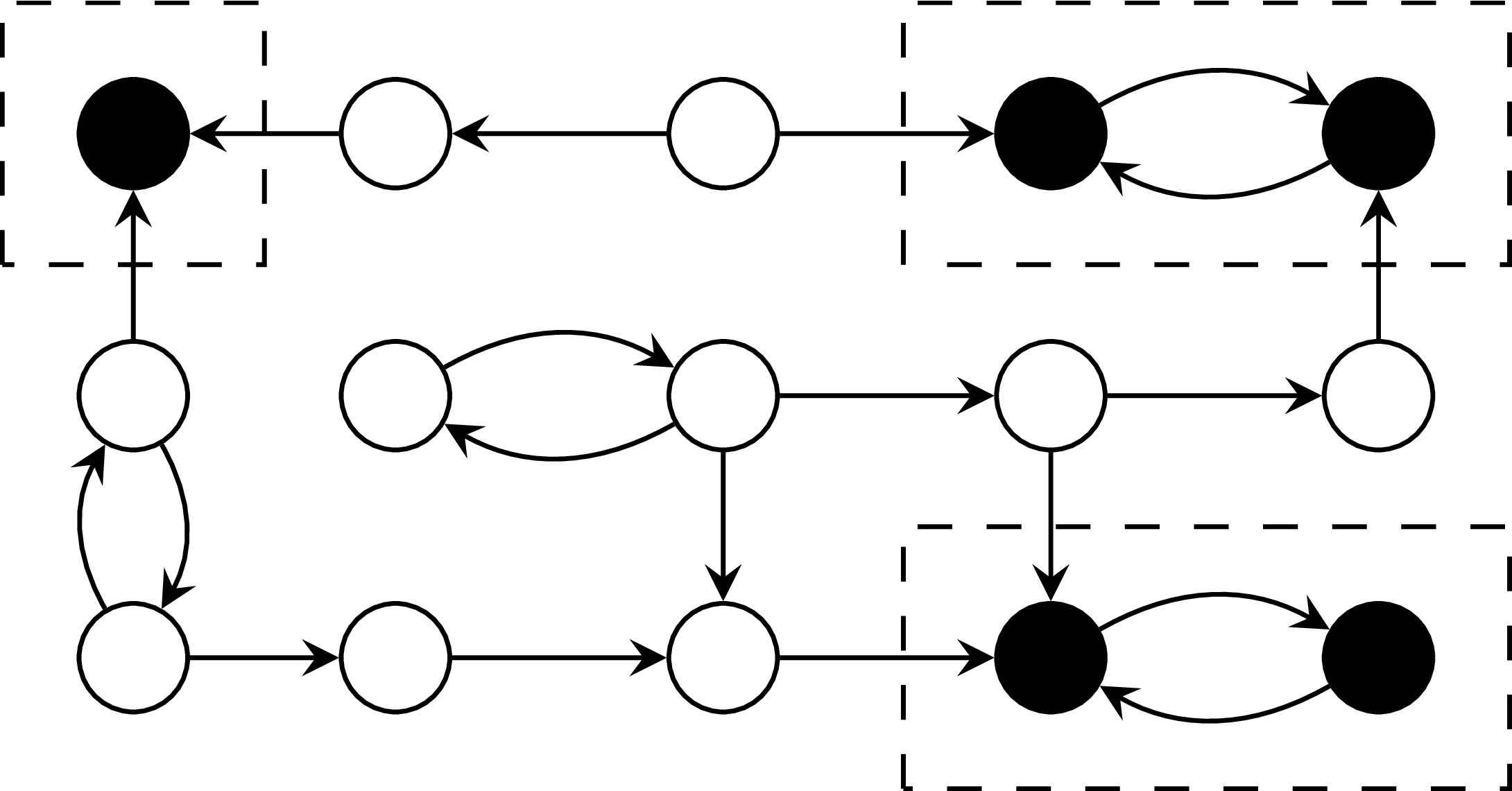
bottom SCC Algorithms

  • Explicit graphs: Tarjan, Kosaraju, or any other linear SCC decomposition is asymptotically optimal.
  • Symbolic graphs: Xie-Beerel is quadratic when computing general SCCs, but linear for just bottom SCCs.

"Optimal" Symbolic Algorithm

Graph
Pivot Vertex ⇒

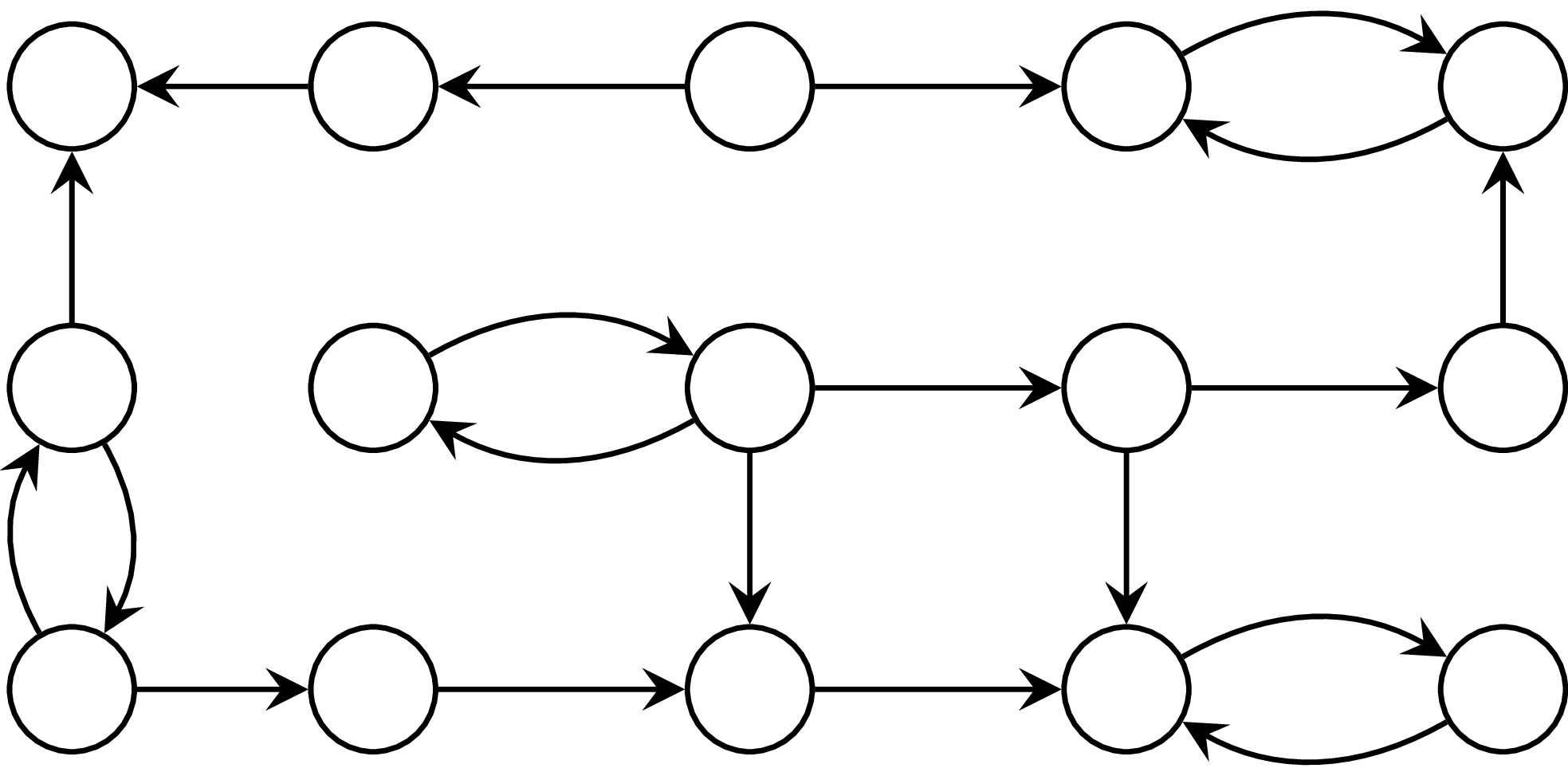
"Optimal" Symbolic Algorithm

Backward set (B) ⇒ 
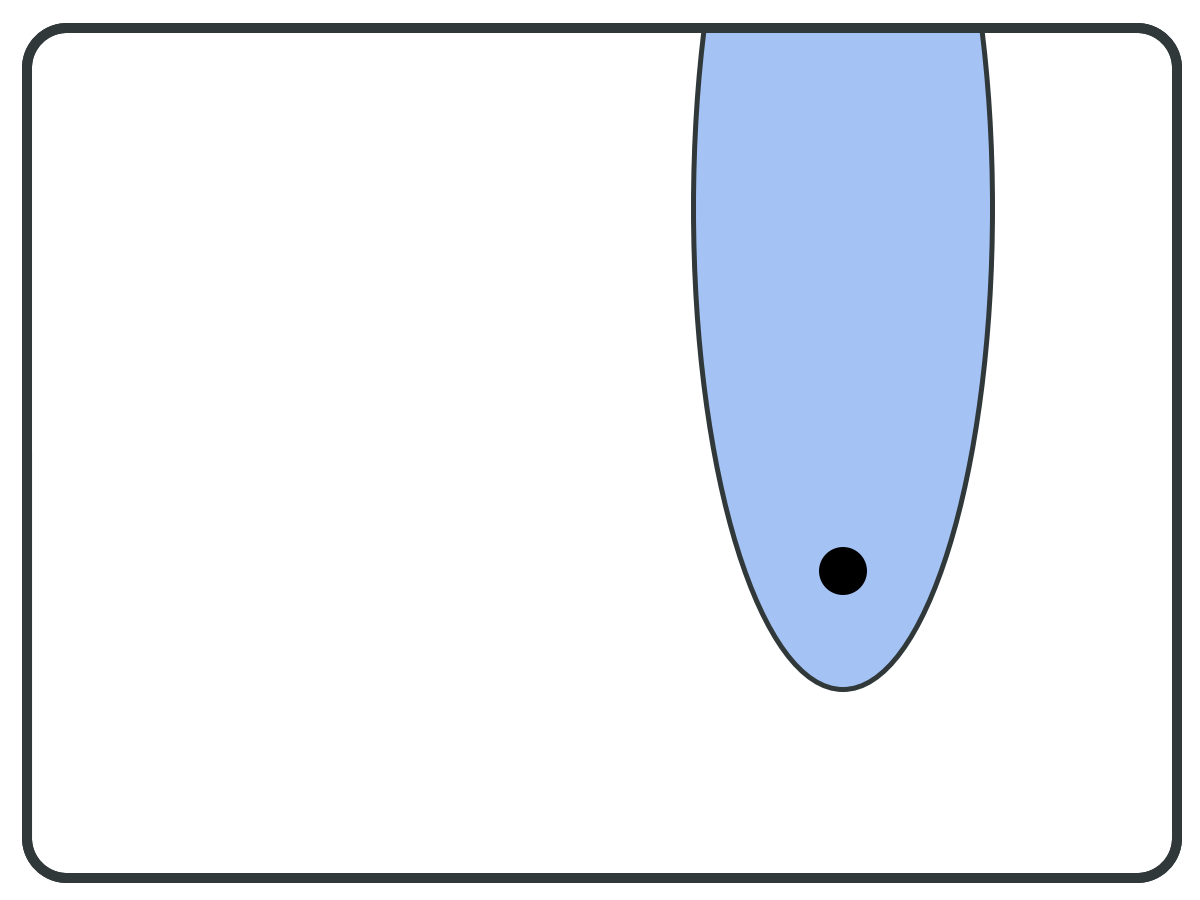
Pivot Vertex ⇒ 
Graph

"Optimal" Symbolic Algorithm

Backward set (B) ⇒ 
Graph
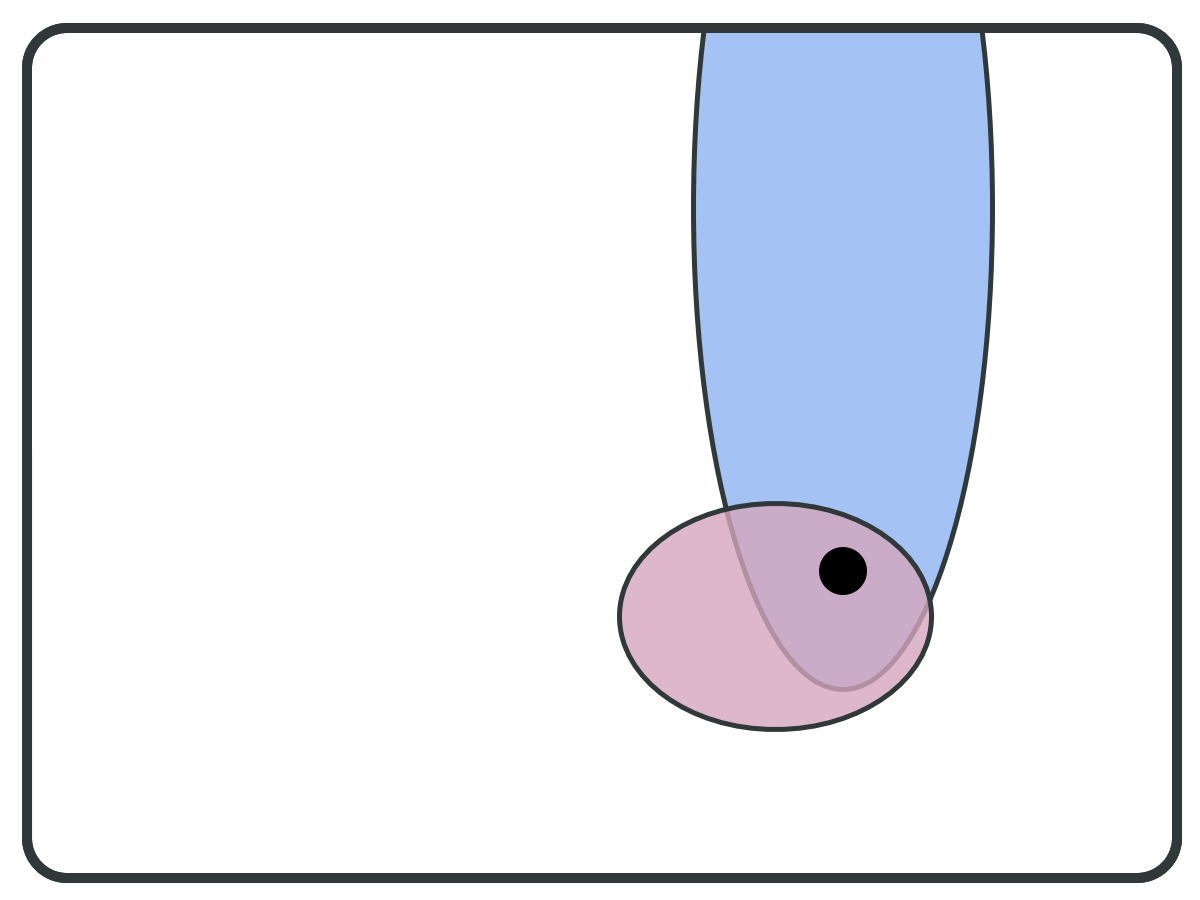
Forward set (F) ⇒

"Optimal" Symbolic Algorithm

Backward set (B) ⇒ 
Graph
Forward set (F) ⇒ 
Not a bottom SCC

"Optimal" Symbolic Algorithm

Graph

×

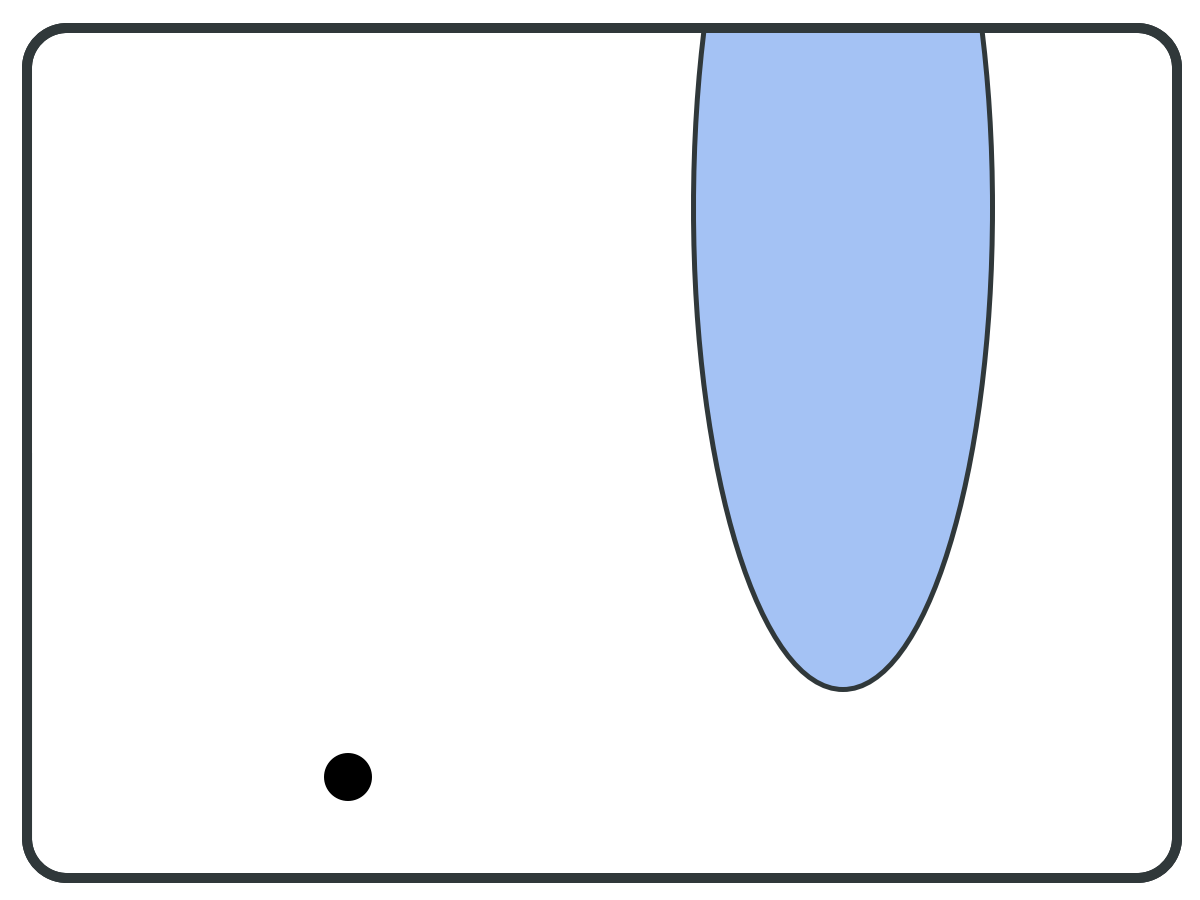
⇐ Pivot Vertex

Large SCC are sometimes small

Graph
10^30
10^10
0.000000000000000001%
⇐

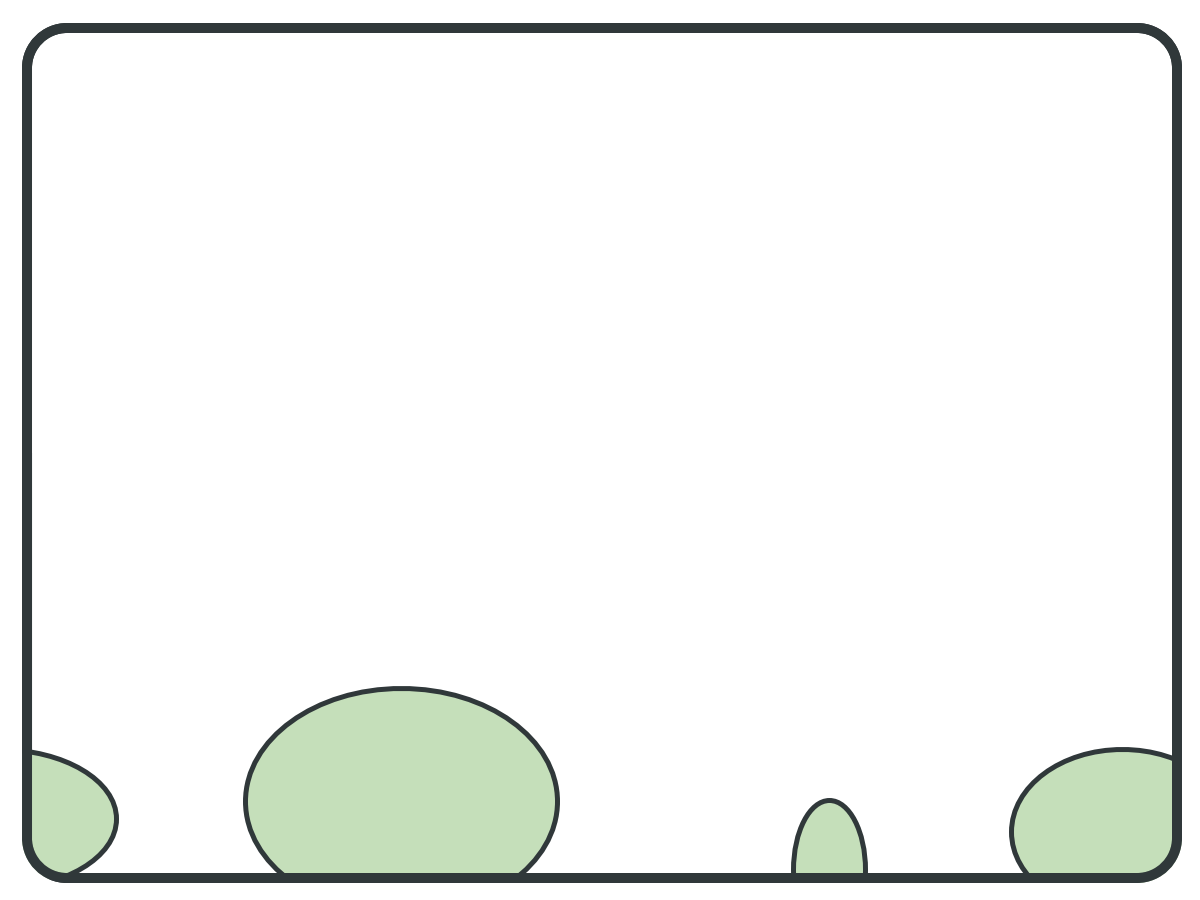
Poor Pivot Selection

Graph

×

×

×

×

×

×

×

×

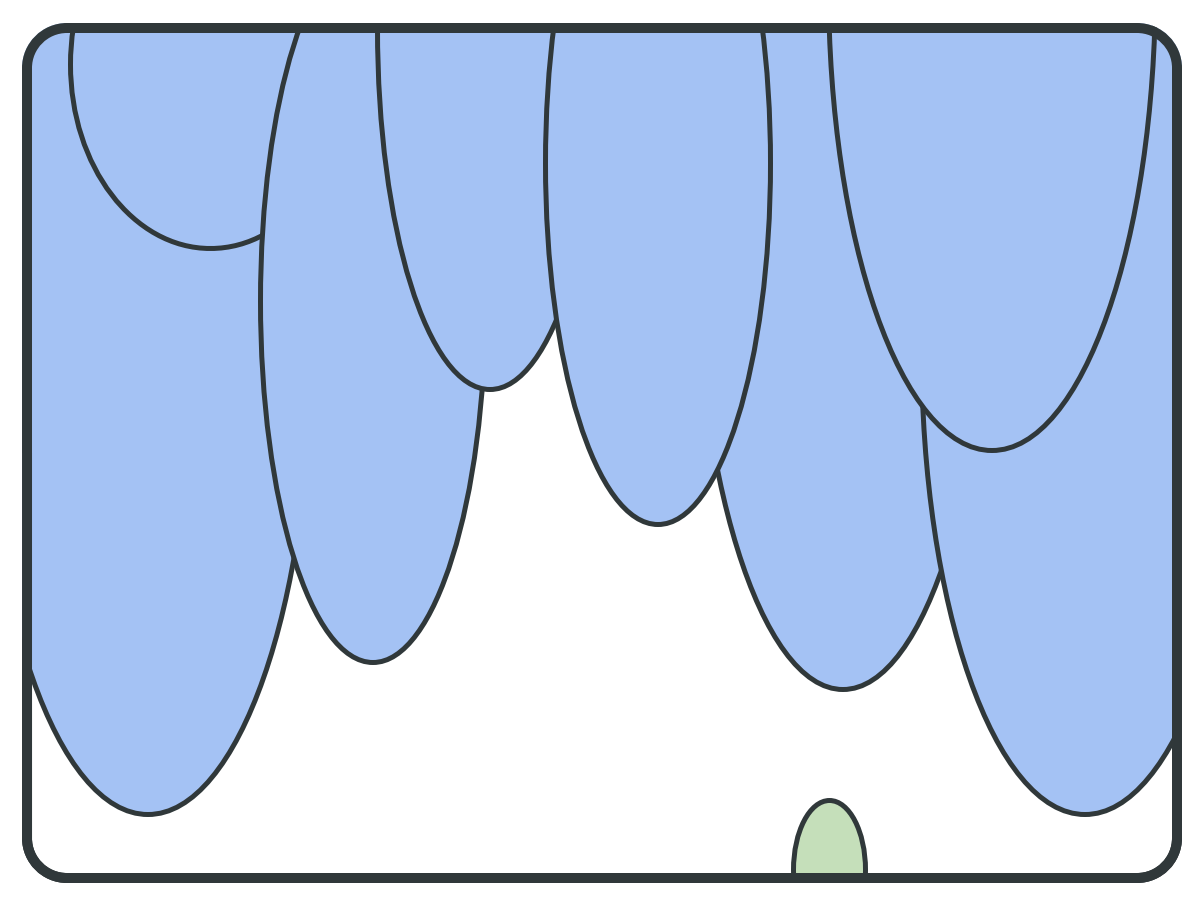
BASIN DIAMETER

Graph
y
x
x << y

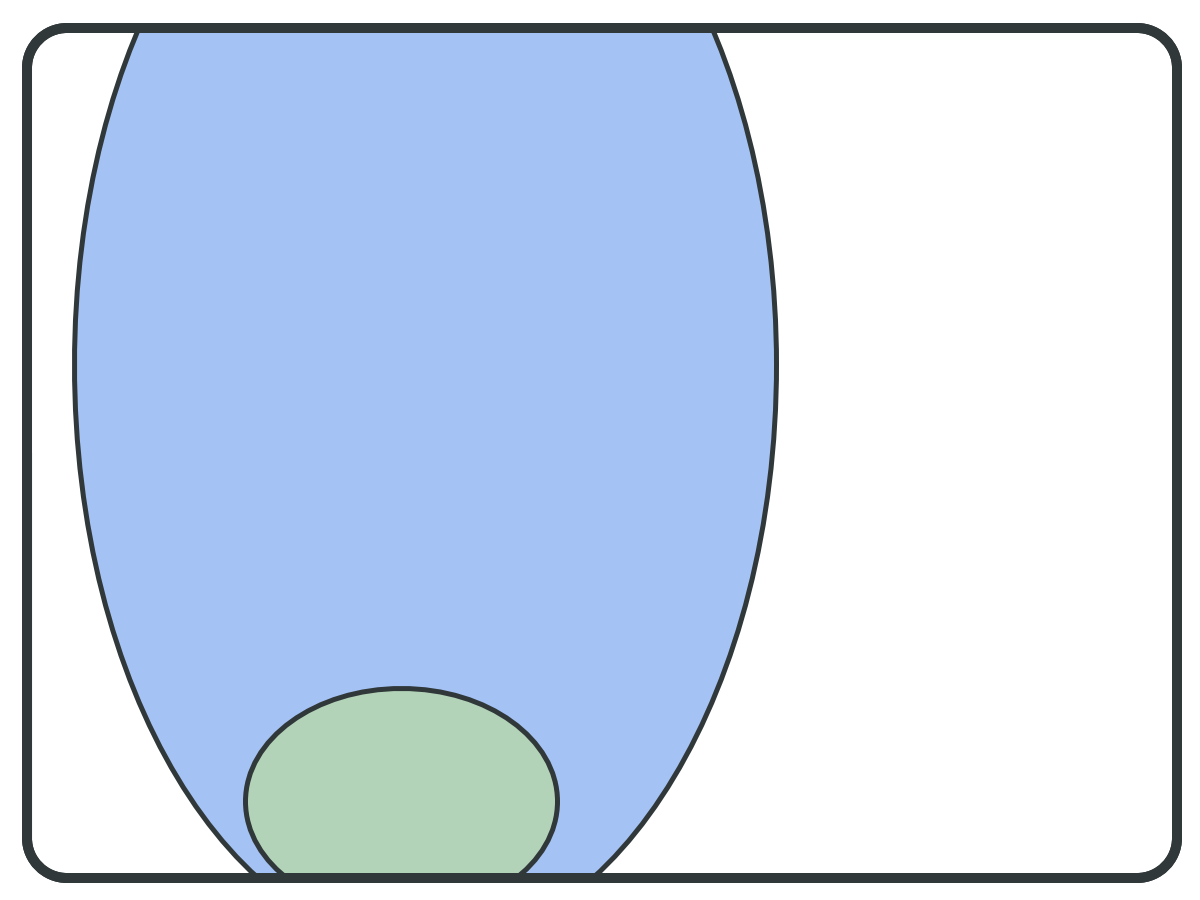
Interleaved Transition Guided Reduction (ITGR)

ITGR: Goal

Graph

×

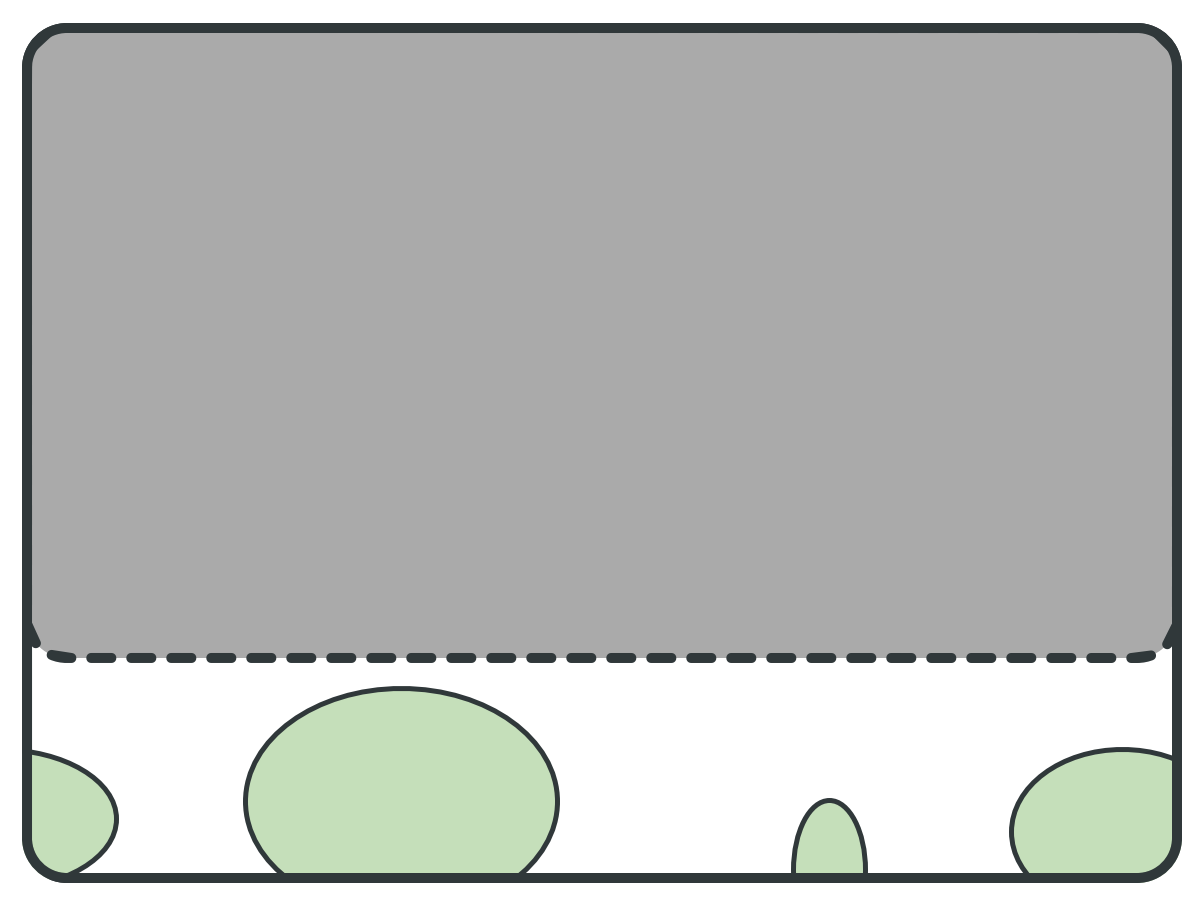
ITGR: Goal

Graph
⇐ Pivot  Set

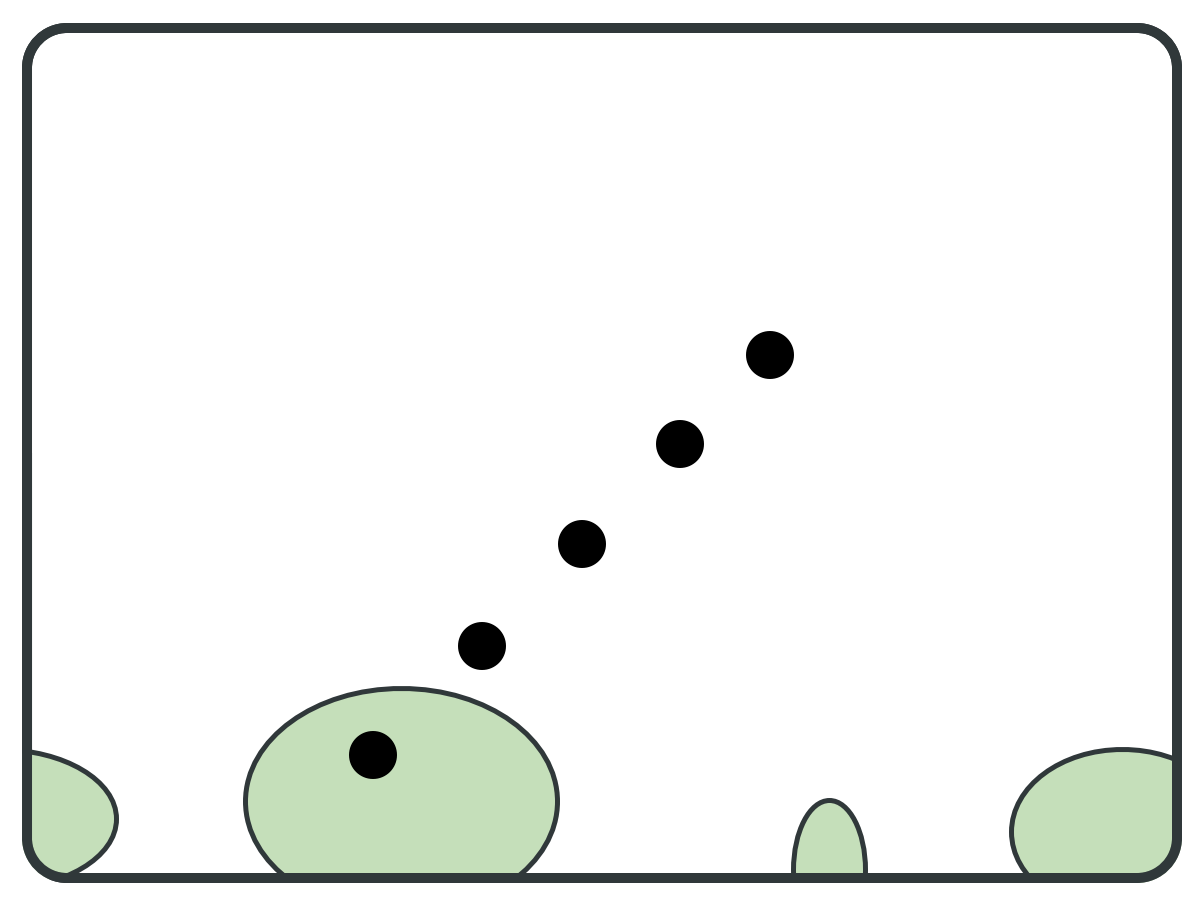
ITGR: Goal

Graph
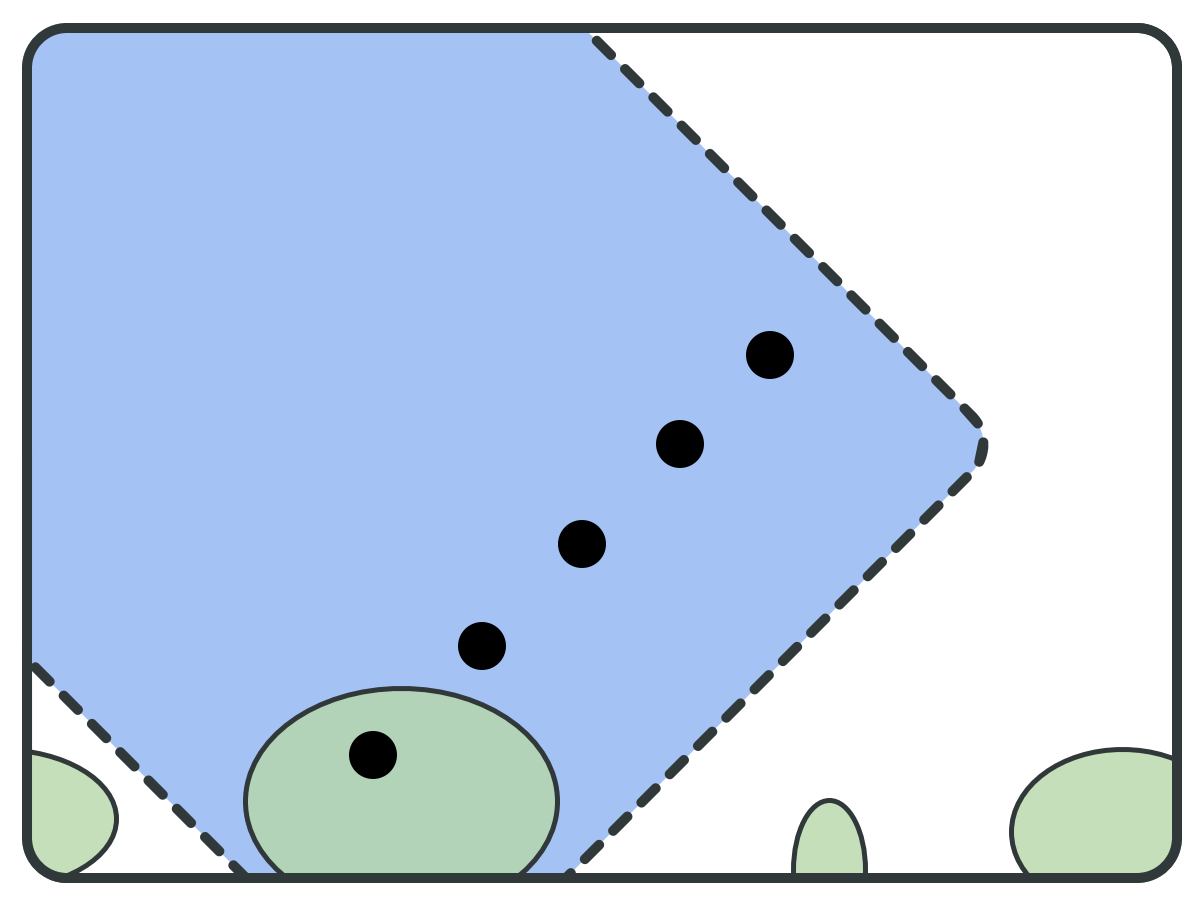
Backward set (B)

ITGR: Goal

Graph
Backward set (B) 
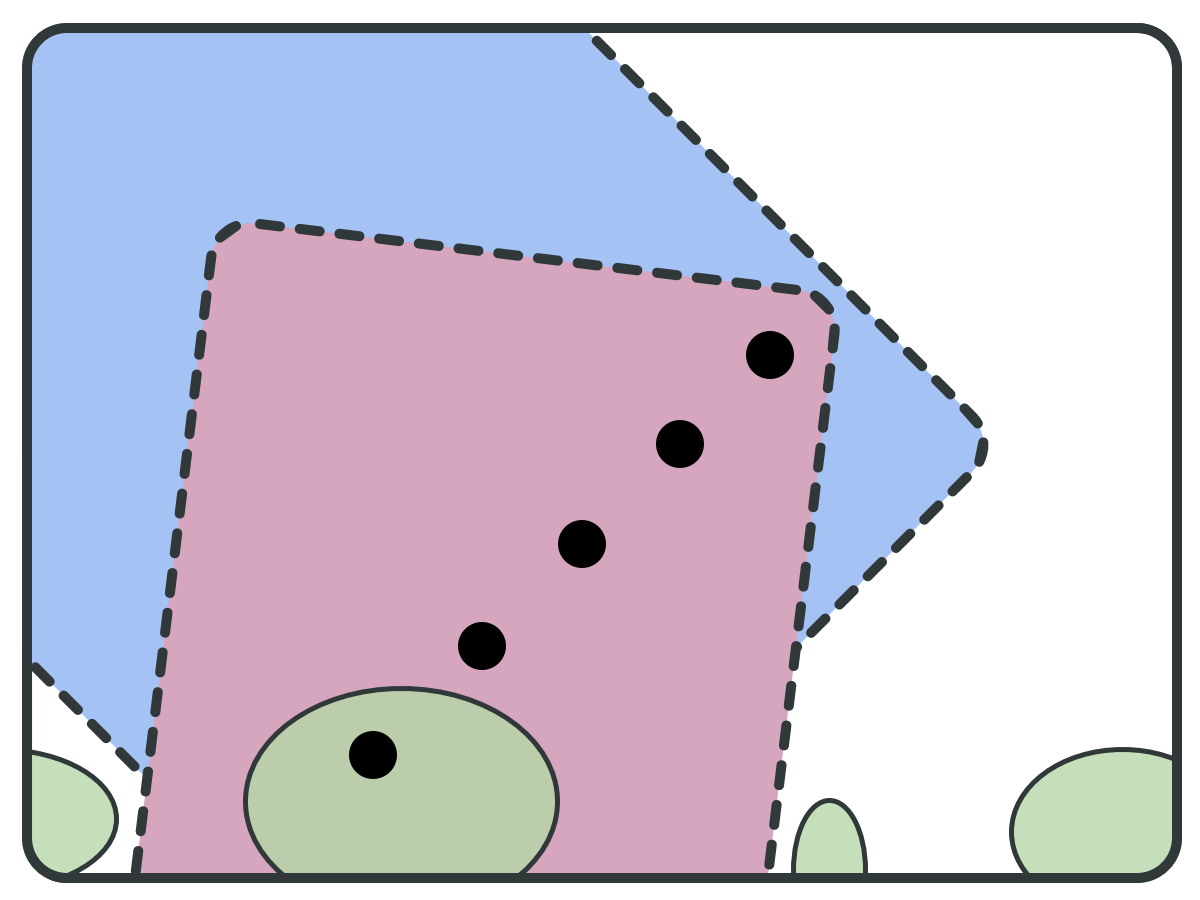
Forward Set 
(F)

ITGR: Goal

Graph
Backward set (B) 
Forward Set 
(F)

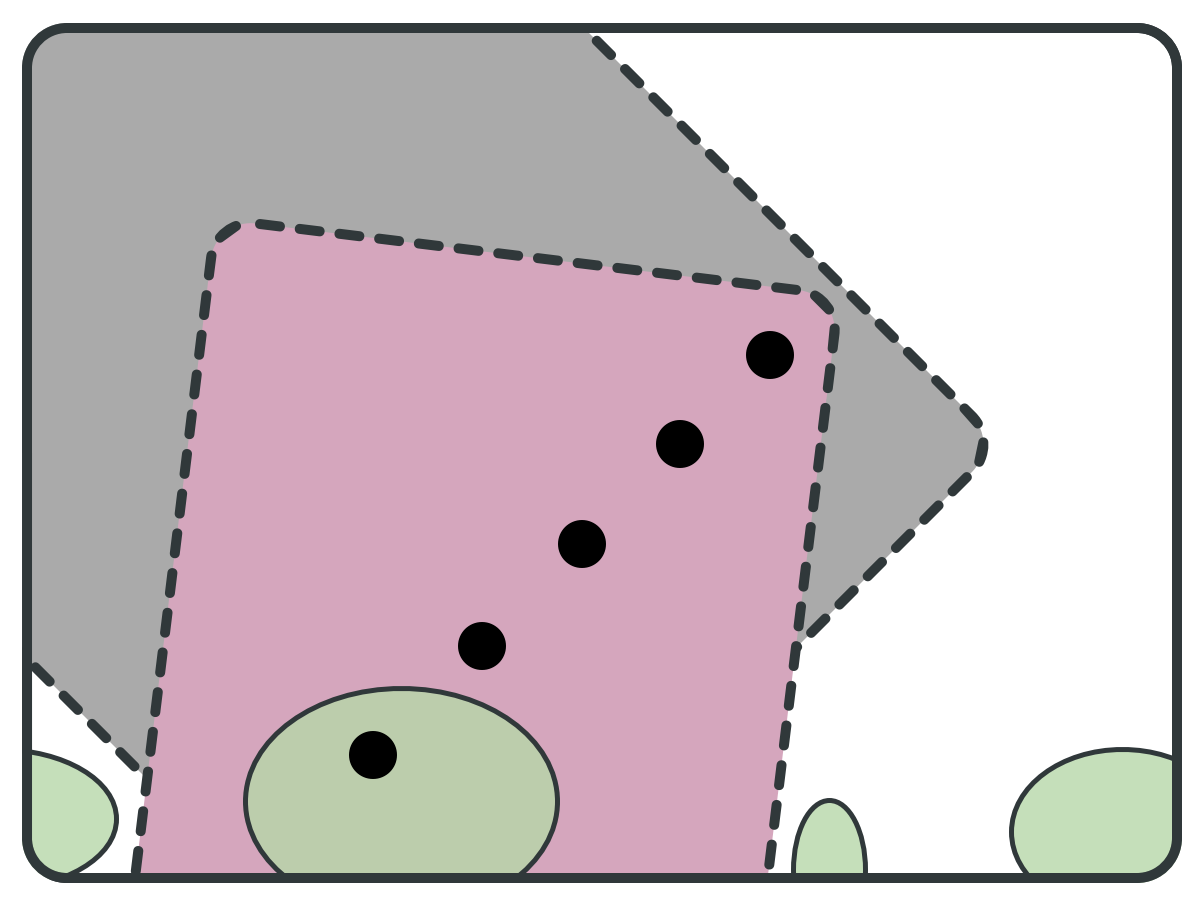
ITGR: Goal

Graph
Backward set (B) 
Forward Set 
(F)

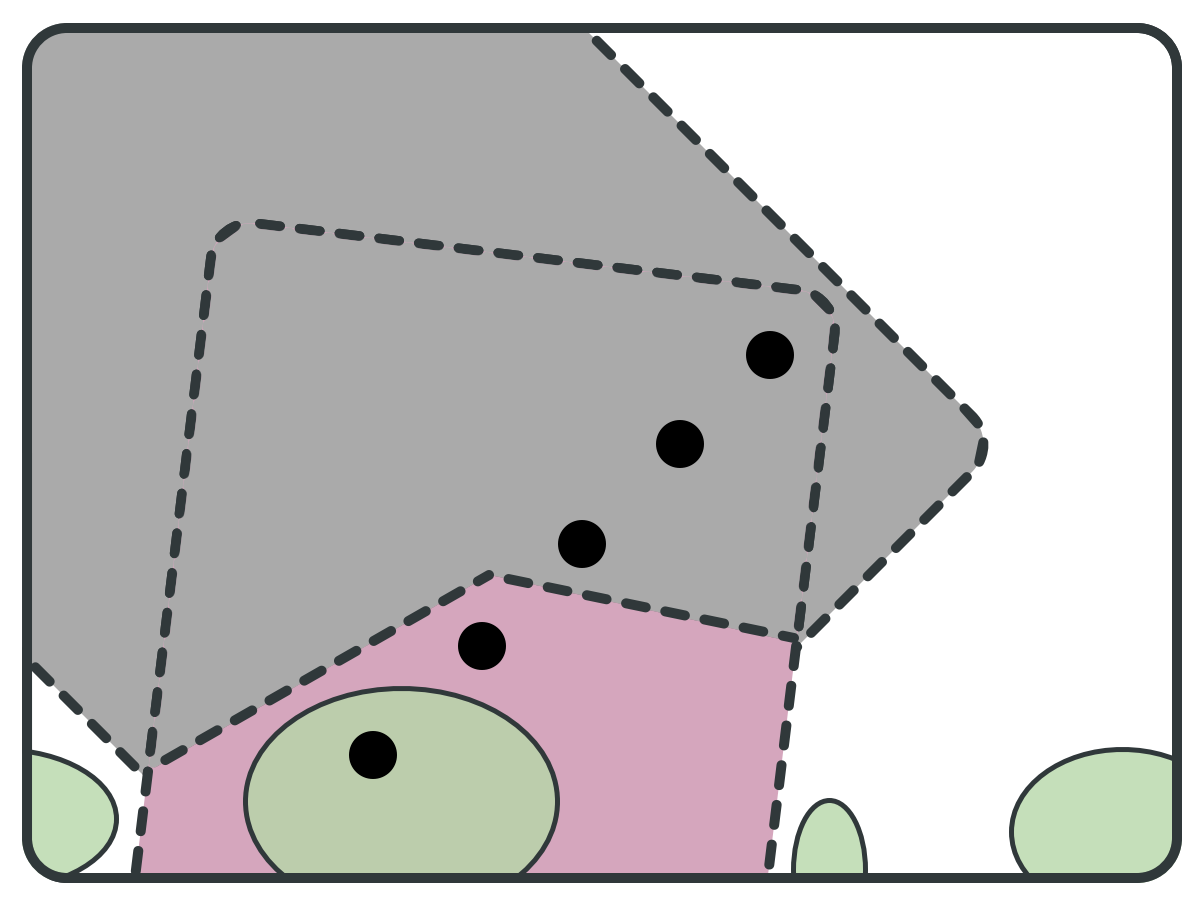
Is it any good?

ITGR: EVALUATION

125 real models, 200 randomly generated

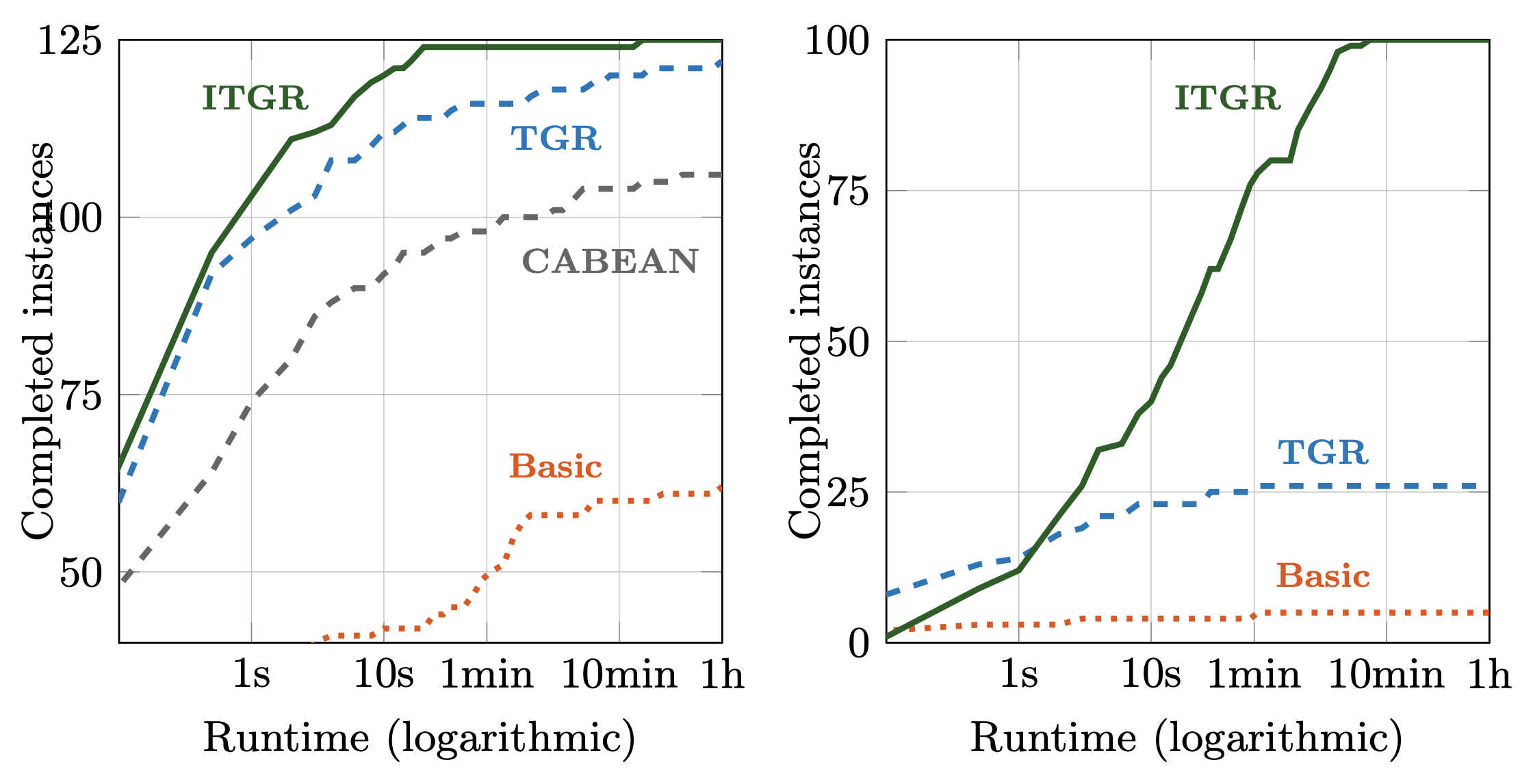
CAV '21 5min

By Samuel Pastva

CAV '21 5min

  • 136

More from Samuel Pastva