Symbolic Encoding of Boolean Networks
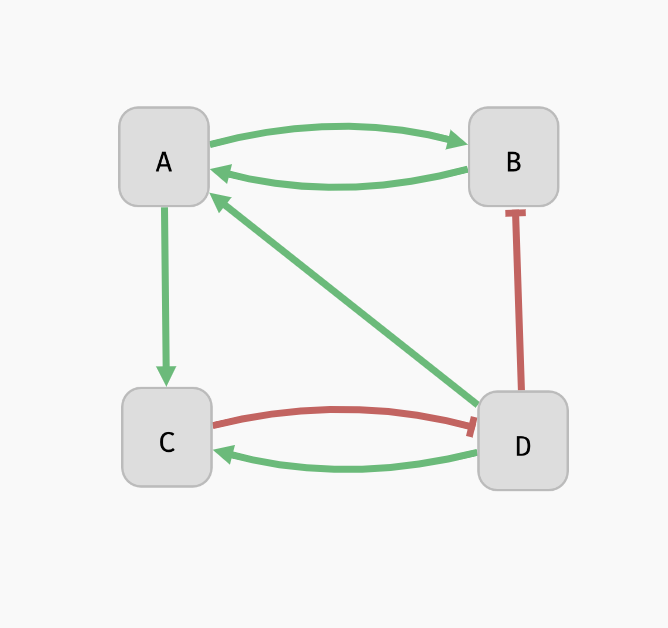
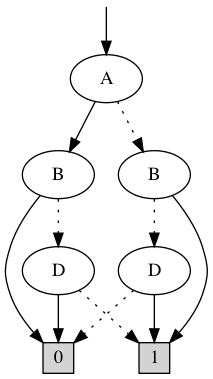
A' = B | D B = A | !D C = A & D D = !C
One attractor...
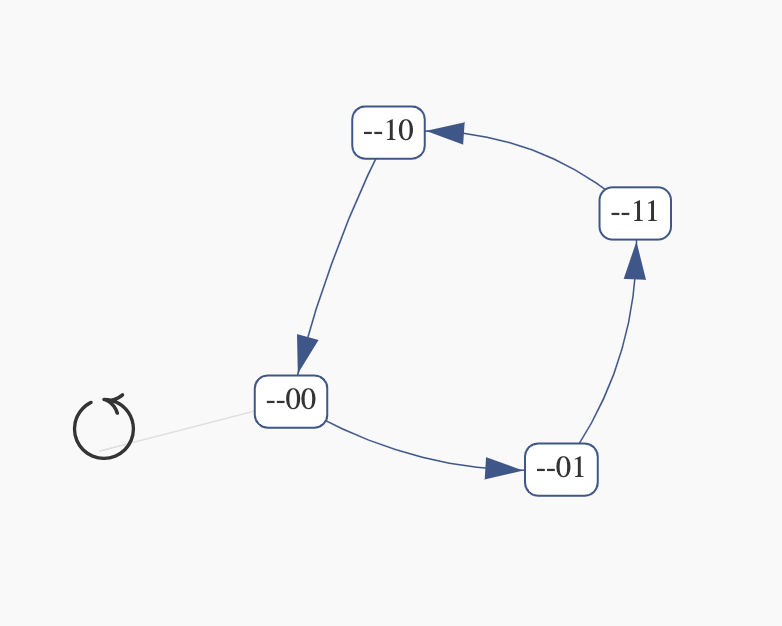
.... as a BDD
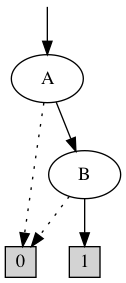
Update function BDD
f_A = B | D ... (f_A = 1 <=> A = 0) | (f_A = 0 <=> A = 1)
"The set of states where applying f_A will change the value of A"
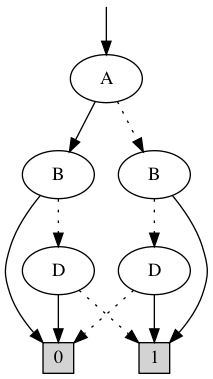
Applying update BDD
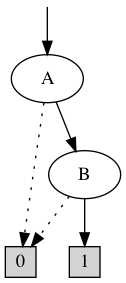
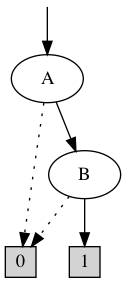
∧
= ∅
"A cannot be updated in the attractor"
... but C can.
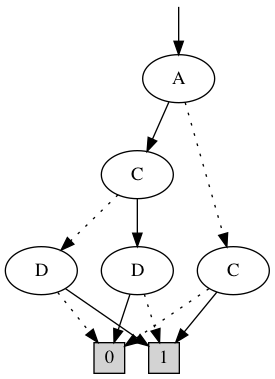
C' = A & D
∧
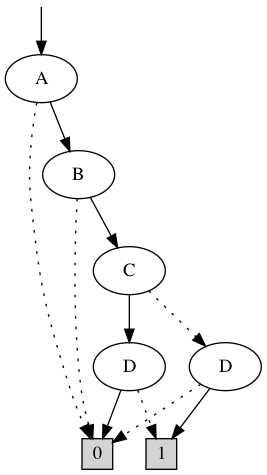
=
We have a set of states that *can* perform a transition. How do we compute the actual successors?
"bit flip C"
operation
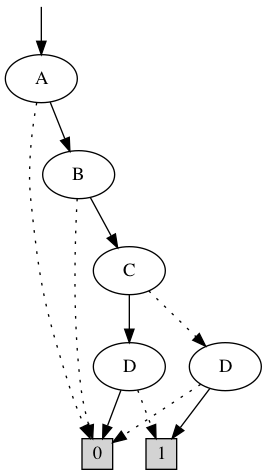
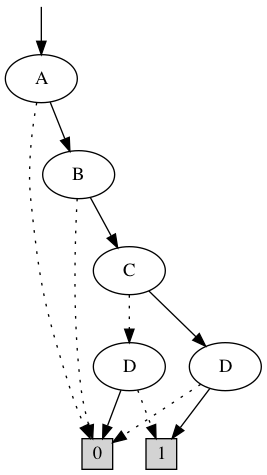
Does this add anything new to the attractor? (It shouldn't...)
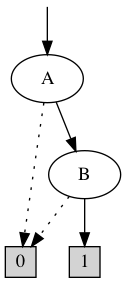
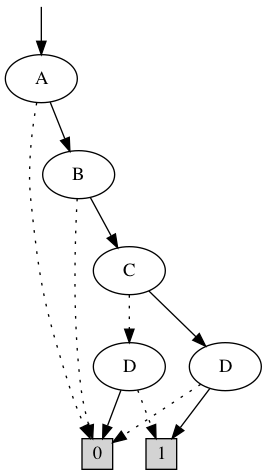

∨
=
What about parameters?

A' = B | D
B = A | !D
C =
(K => (A & D)) & (!K => (A | D))
D = !C
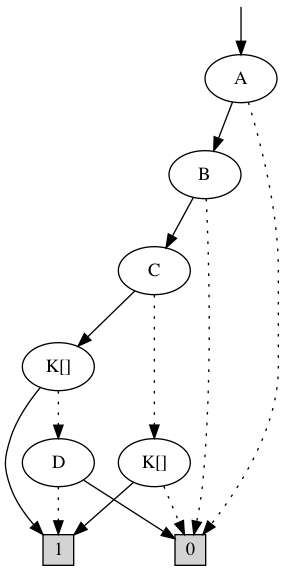
There is a K in the BDD now.

Writing K everywhere becomes boring very quickly....

A' = B | D B = A | !D C = f(A, D) D = !C
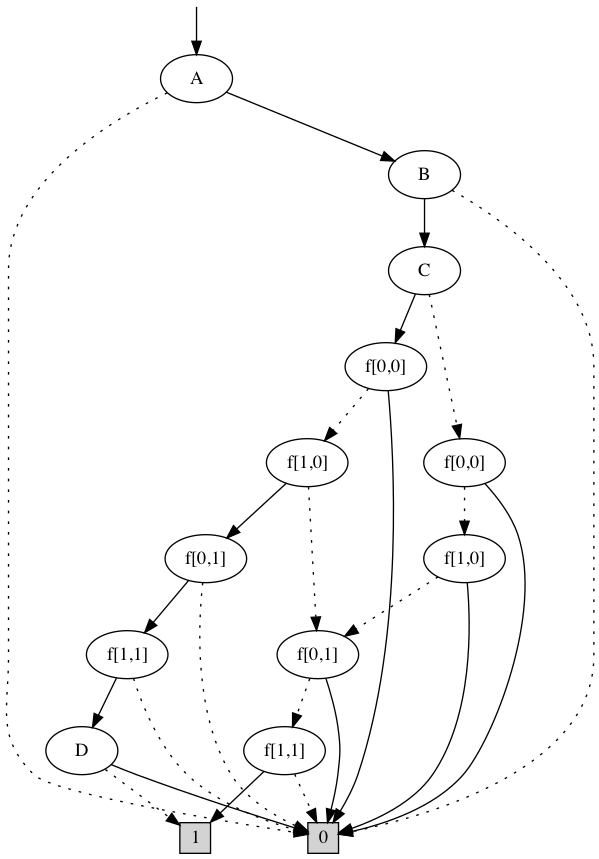
Now we have 4 parameters in the BDD: A | B | F(A, B) --------------- 1 | 1 | f[1,1] 1 | 0 | f[1,0] 0 | 1 | f[0,1] 0 | 0 | f[0,0]
(for binary functions this is pretty useless, but with more arguments, there isn't a much better option)
Update functions work exactly the same way, except they contain parameters:
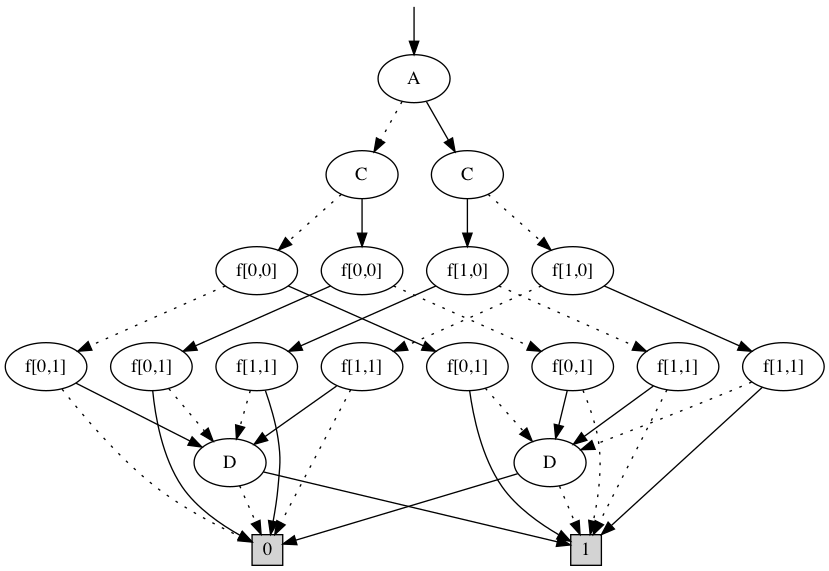
C' = f(A, D)
And now for something completely different...
Symbolic Attractor Detection
A lot of *large* sets have a very compact BDD, and a lot of *small* sets have ugly exponential BDDs.
Solving a "bigger", more general problem symbolically may be easier than computing it exactly.
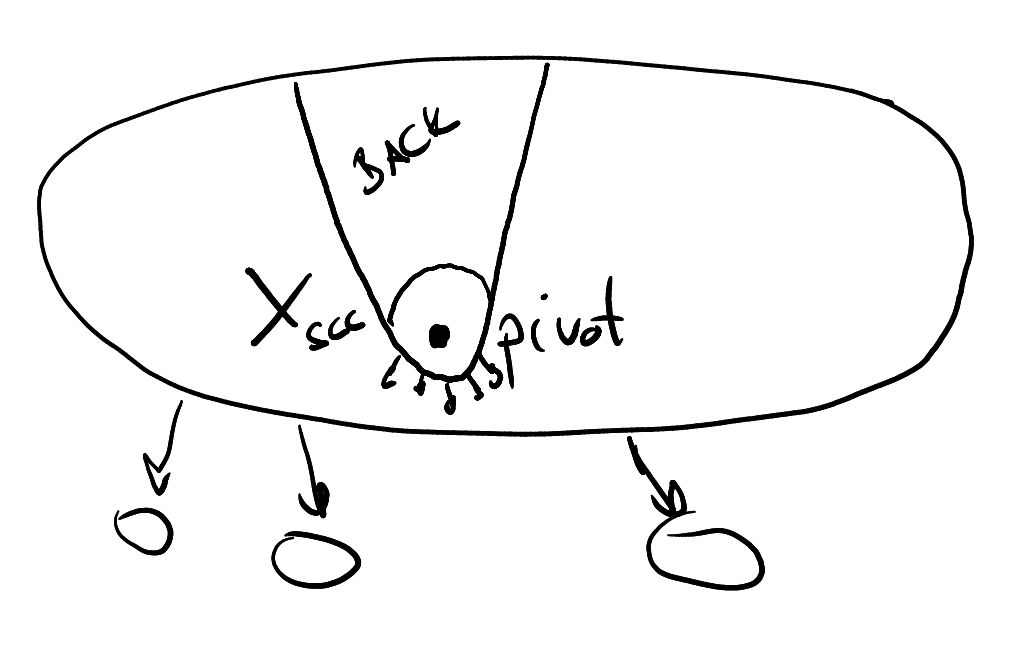
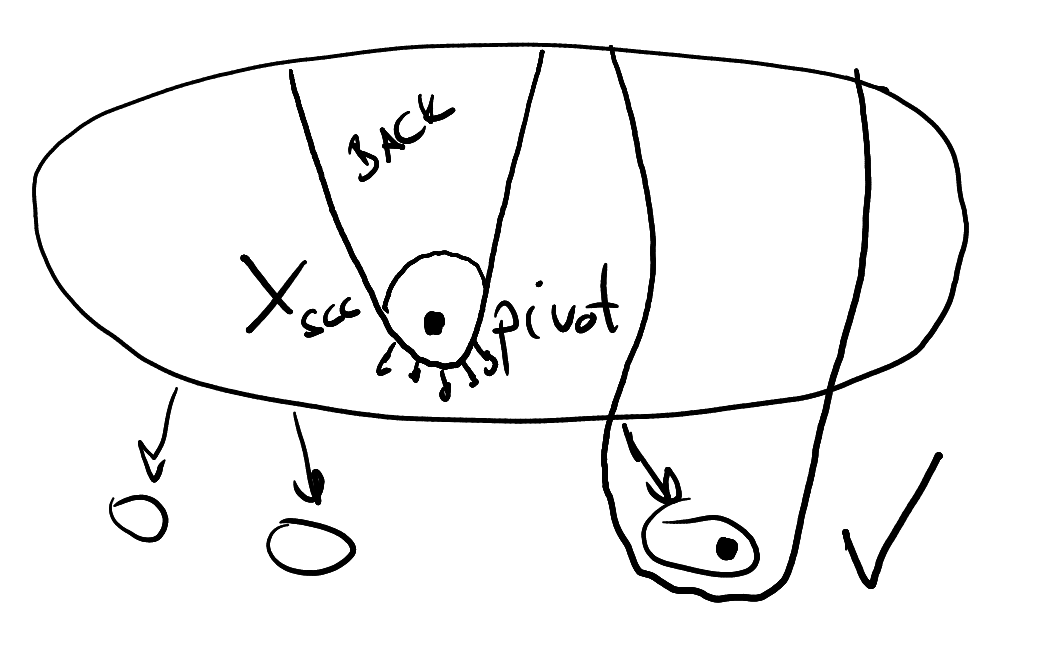
Symbolic Encoding of Boolean Networks
By Samuel Pastva
Symbolic Encoding of Boolean Networks
- 150



