High-dimensional estimation - Lasso
Study Group on Learning Theory
Daniel Yukimura

Chapter 8: Sparse methods
\bullet \hspace{2mm} \text{Standard supervised learning has excess risk:}\\ R(\hat{\theta}) - R^* \sim \dfrac{d}{n}, \hspace{2mm} n^{-\frac{2}{d+2}}, \dots
dimensionality
problem
\text{\textbf{Variable Selection:}}
Features
select relevant features
Inference
\text{8.2 - Variable selection by } \ell_0 \text{ penalty}
\bullet \hspace{2mm} \ell_0 = \text{``number of nonzero entries"}
\bullet \hspace{2mm} \text{Excess risk:} \hspace{2mm} R(\hat{\theta})-R^* \sim \dfrac{\sigma^2 k \log(d)}{n}
\bullet \hspace{2mm} \text{No assumption over the design matrix } \Phi
\bullet \hspace{2mm} \text{ Algorithms may take exponential time on } d
\text{8.3 - Variable selection by } \ell_1 \text{ penalty}
Lasso - Least absolute shrinkage and selection operator
\min\limits_{\theta} \hspace{1mm} \frac{1}{2 n} \| y - \Phi \theta \|_2^2 + \lambda \|\theta\|_1 \hspace{6mm} \footnotesize{(L)}
\bullet \hspace{2mm} \|\cdot\|_1 \text{ promotes sparsity.}
\bullet \hspace{2mm} \text{Convex problem with tractable algorithms.}
\bullet \hspace{2mm} \text{Requires assumptions on } \Phi \text{ to obtain fast rates.}
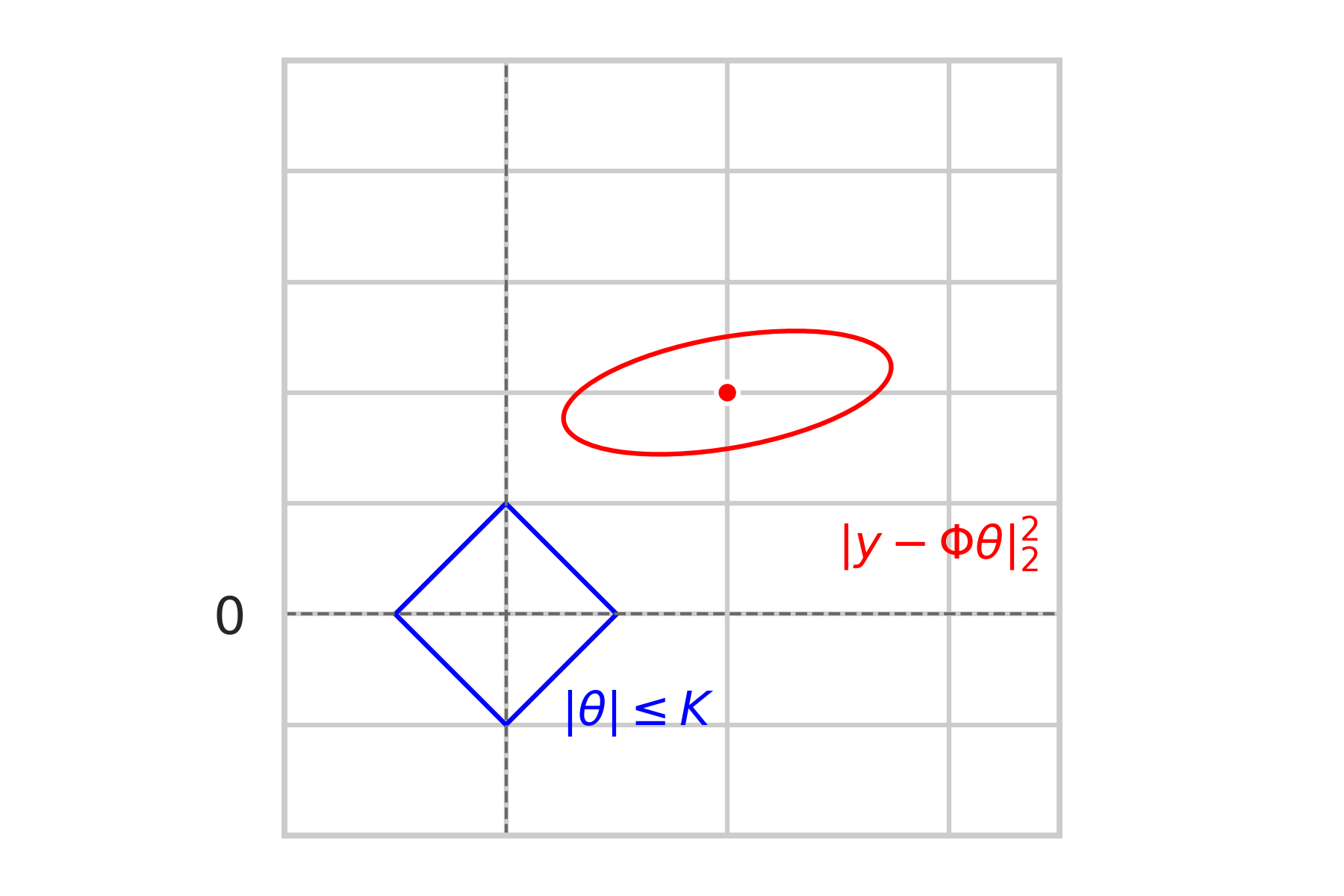
\textbf{Sparcity-inducing effect}
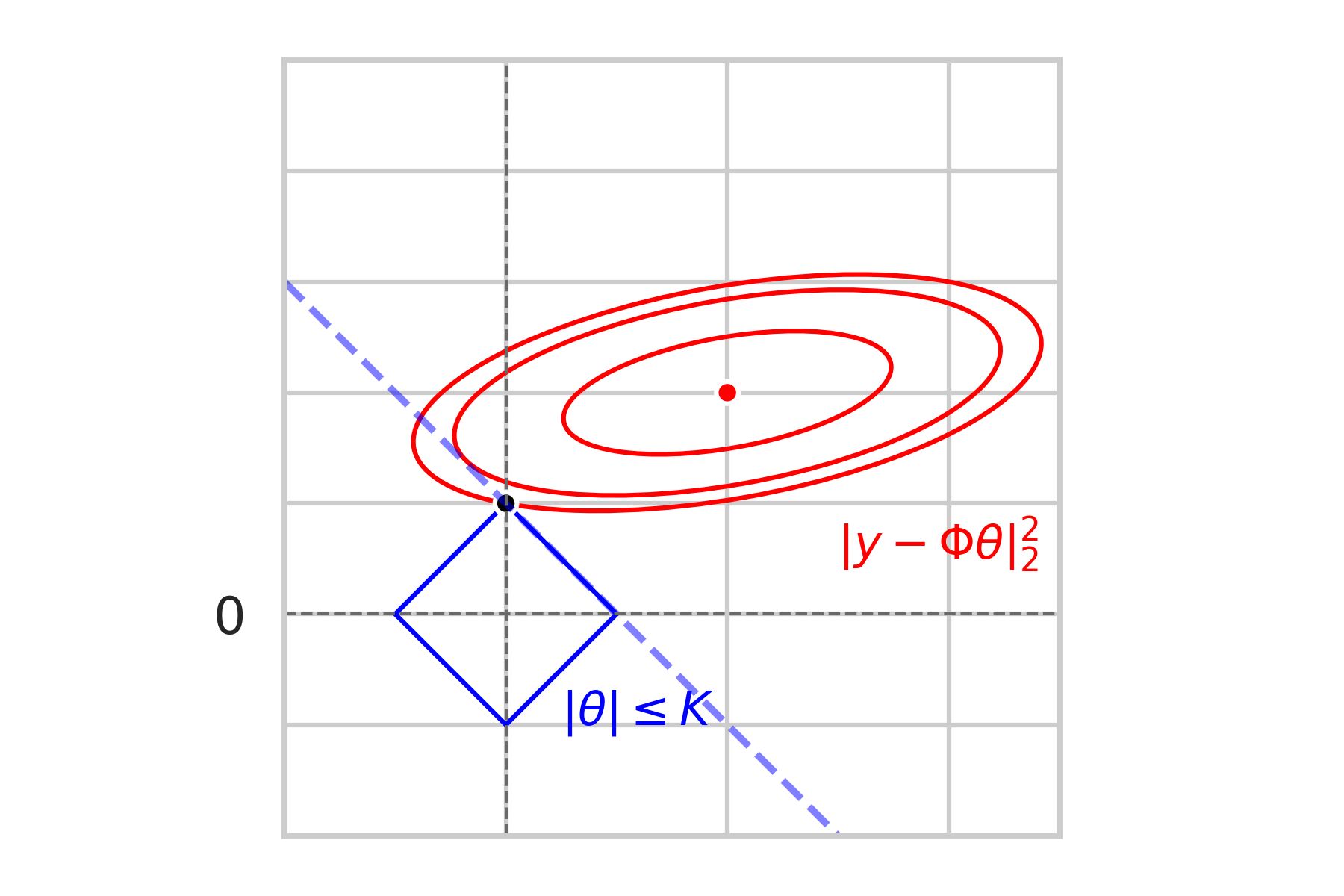
\text{Geometric Intuition:}
\min\limits_{\|\theta\|_1\leq K} \|y - \Phi\theta\|_2^2
\text{Constrained problem:}
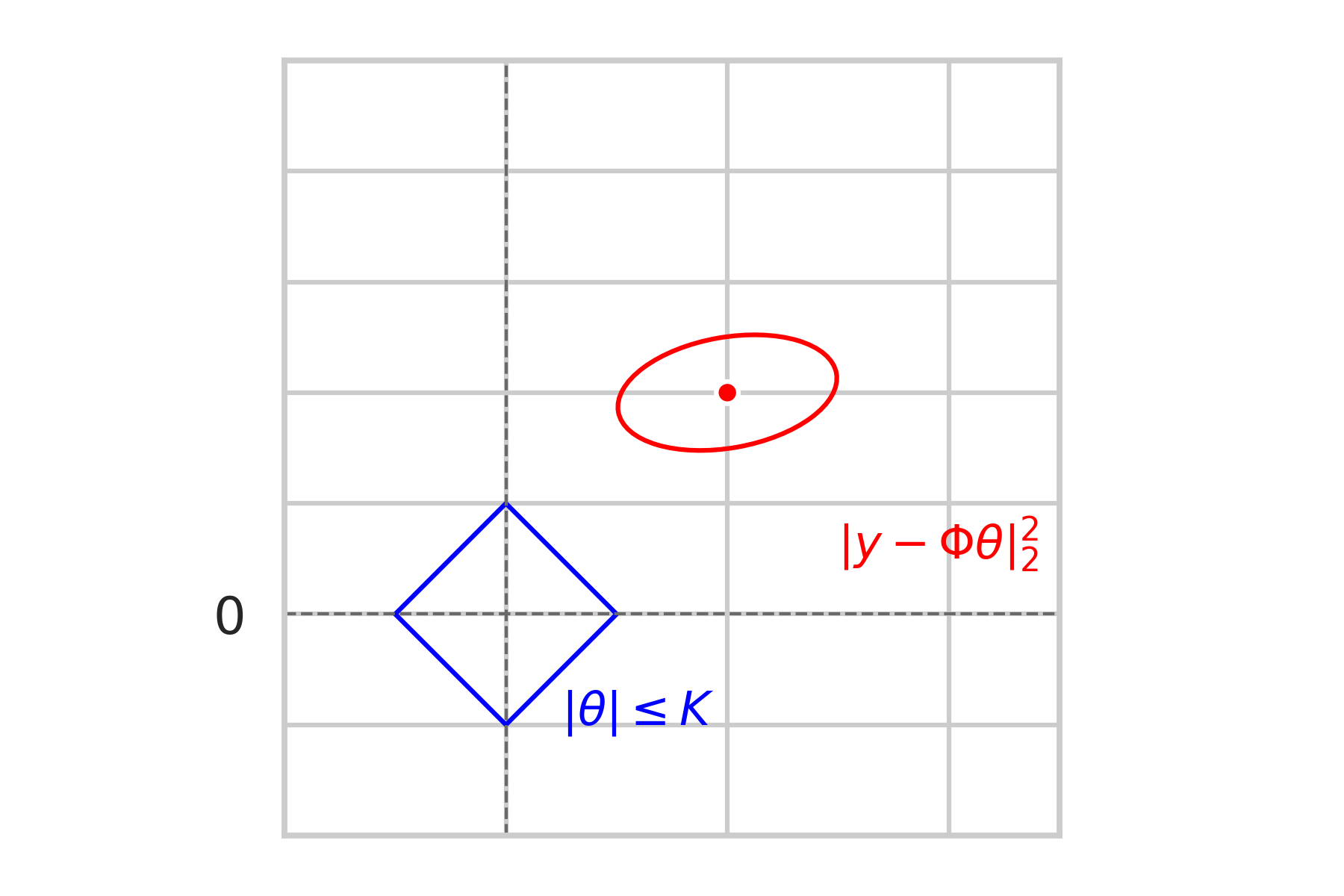
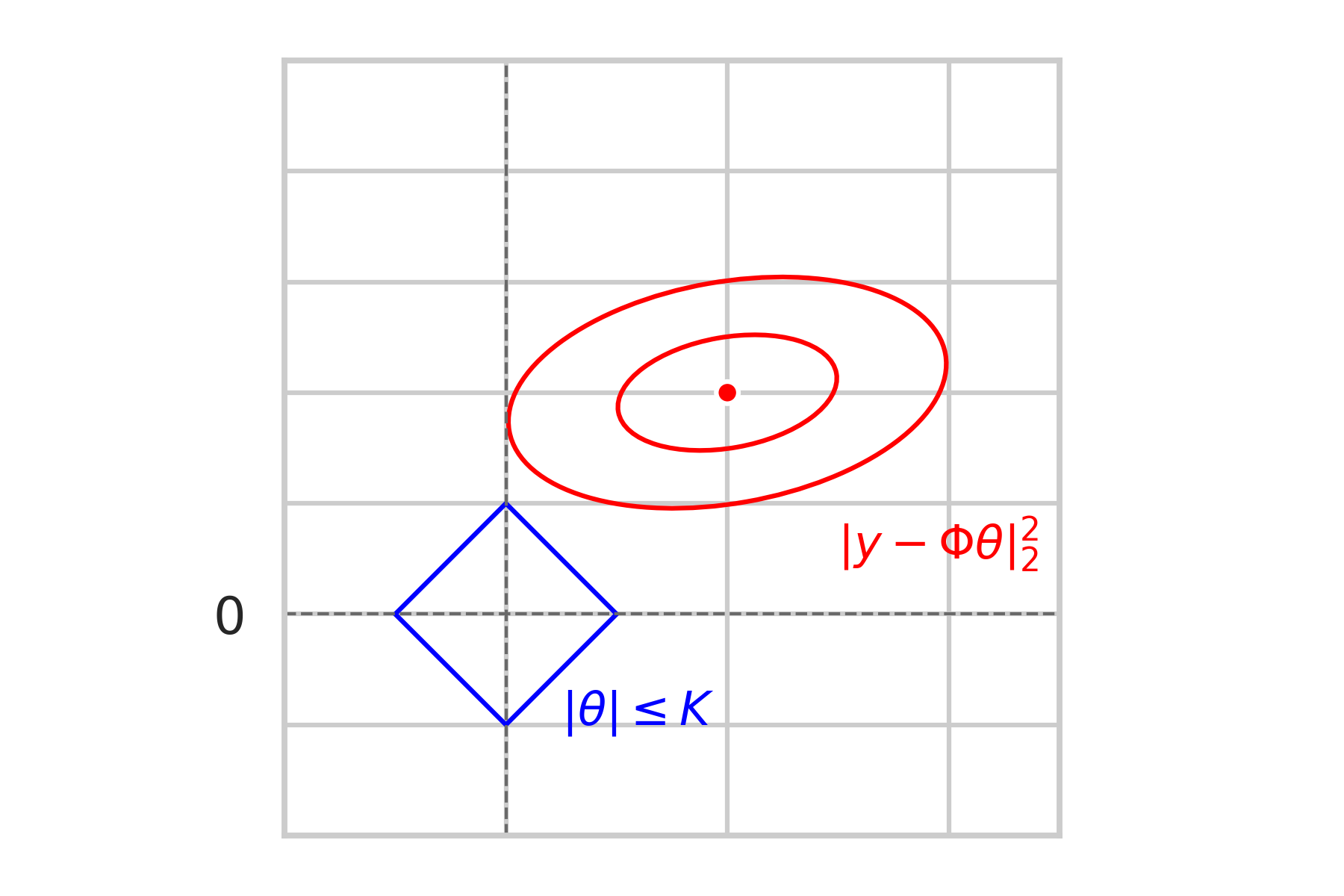
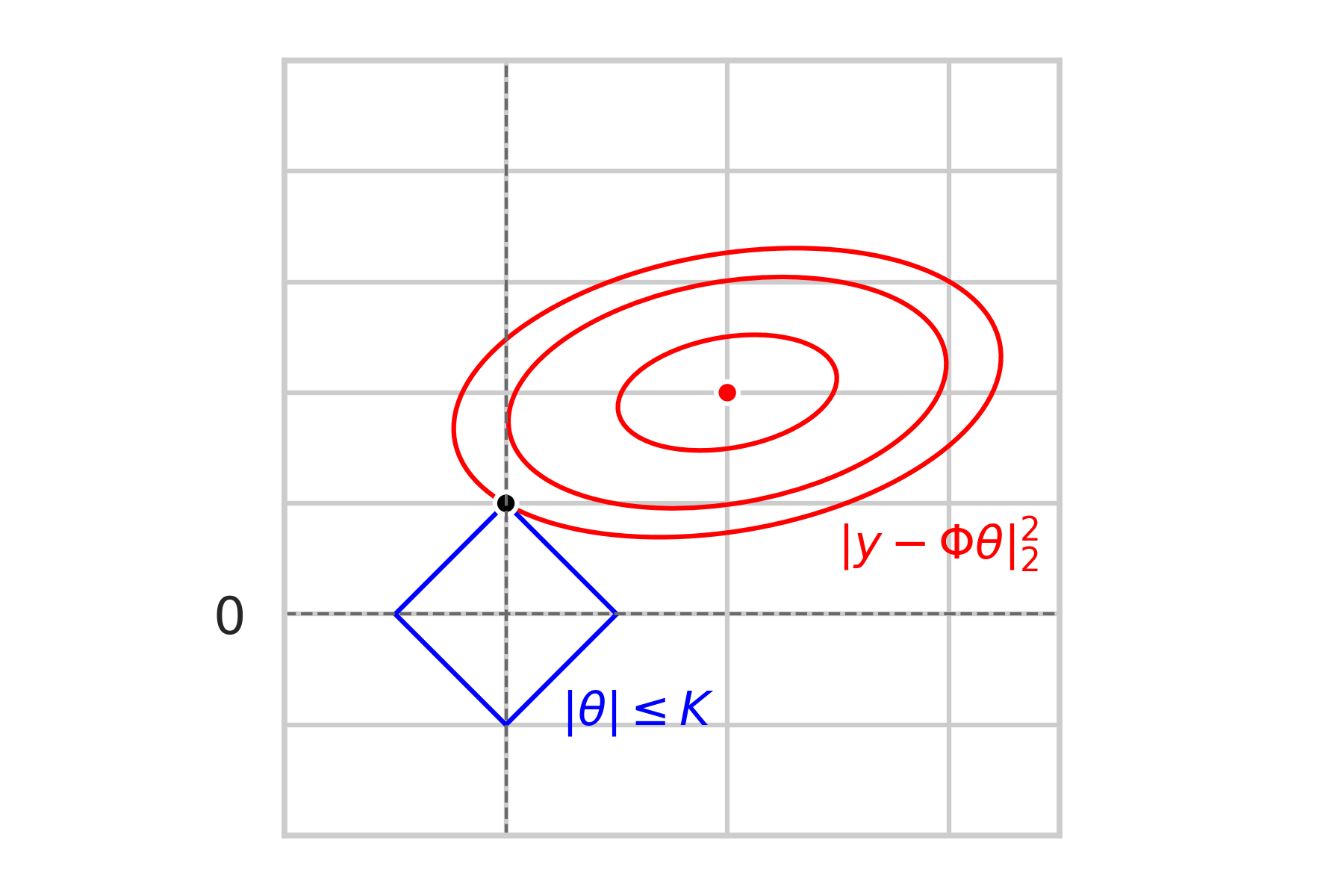
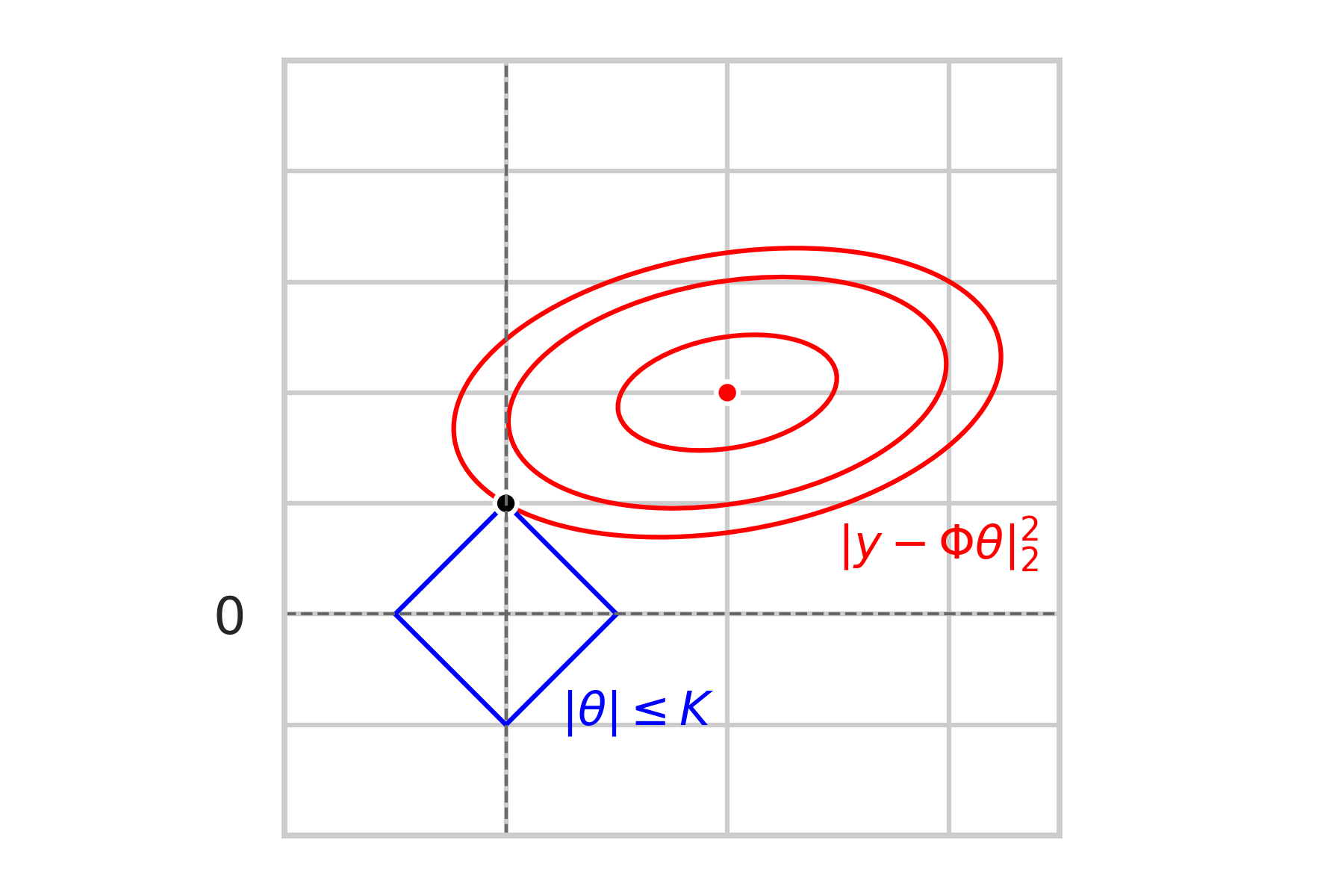
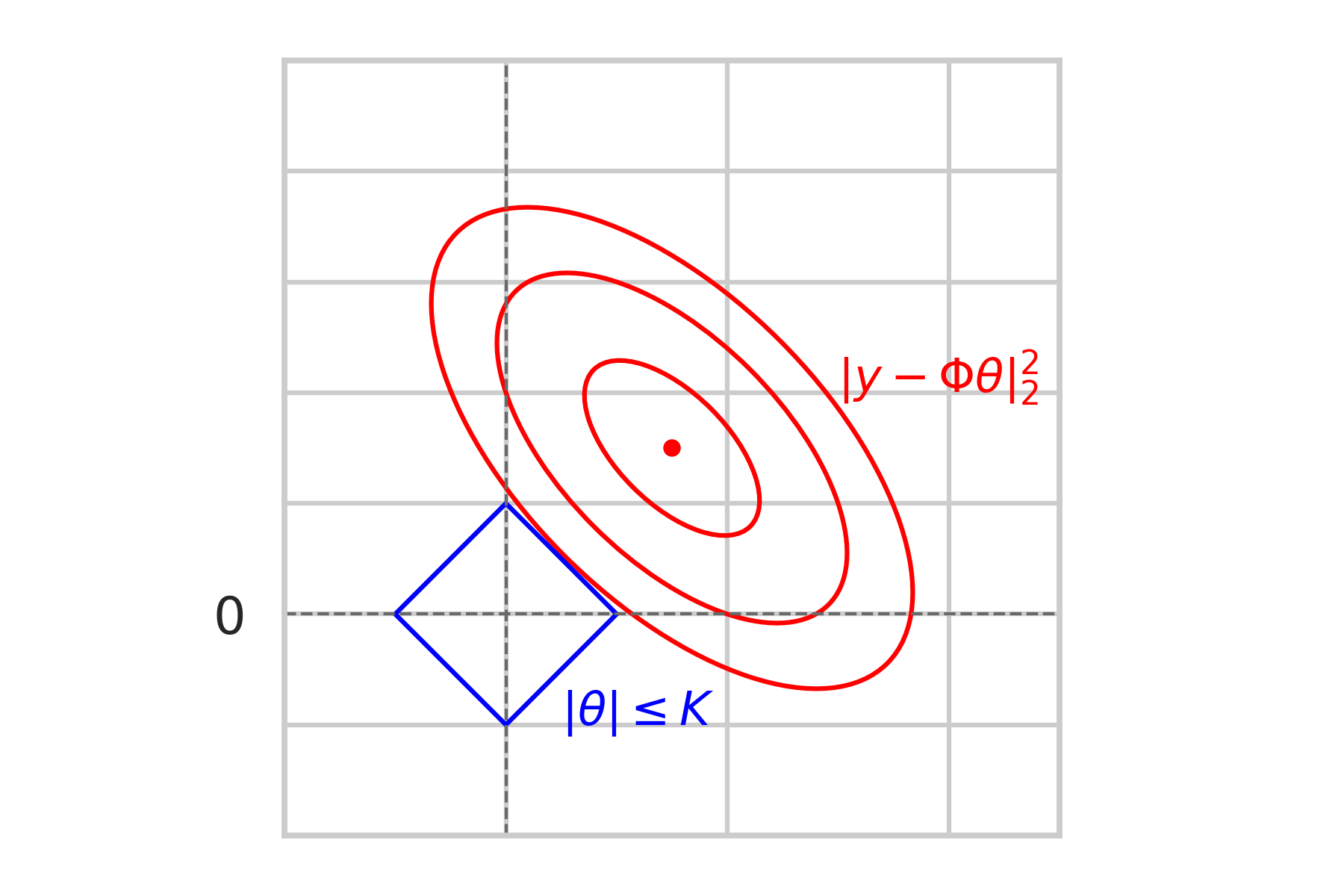
non-sparse
sparse
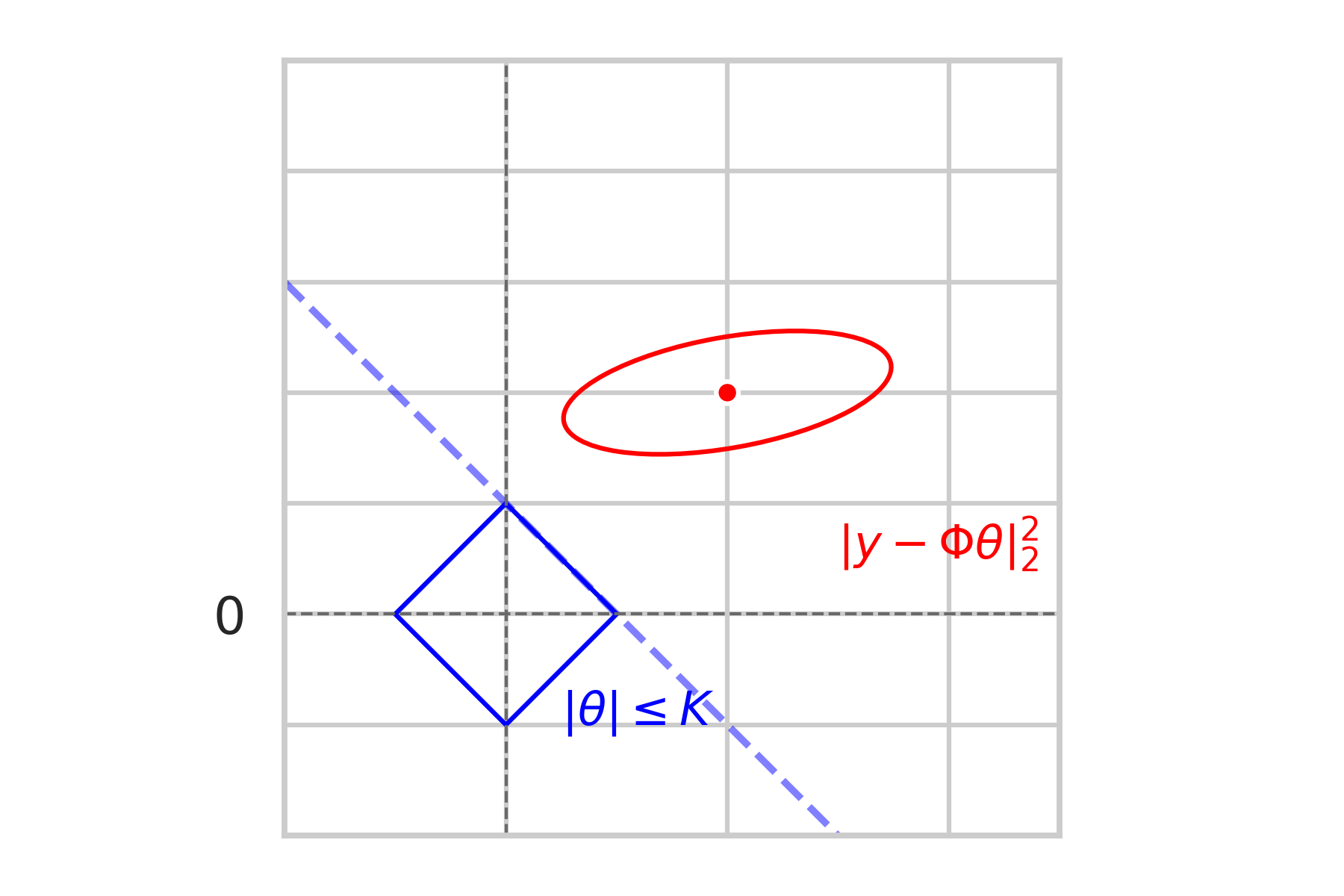
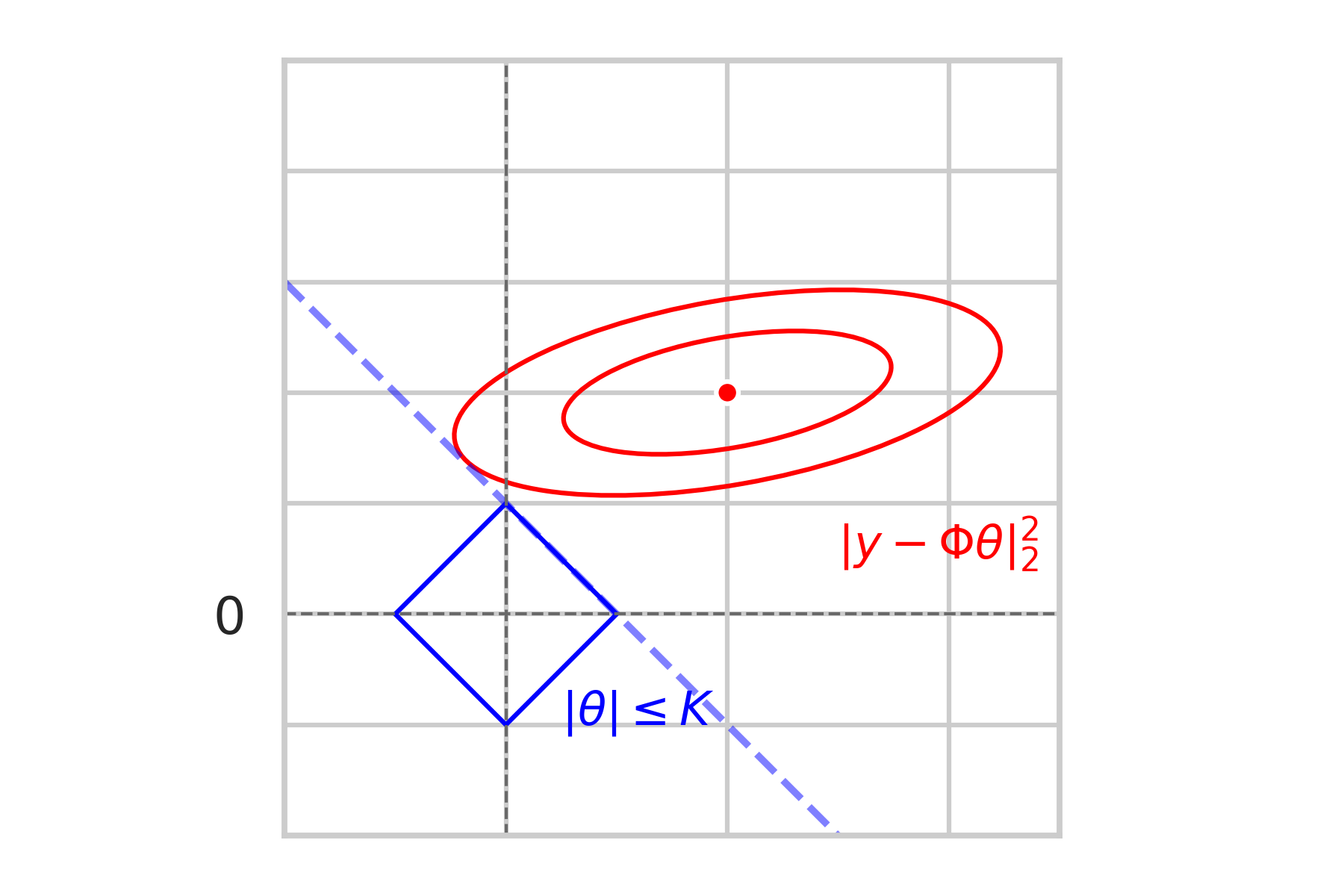
\mathcal{L} = \text{``Extended line from } F \text{ "}
\mathbb{P} \left[\hat \theta \in F\right] \leq \mathbb{P} \left[\hat \theta \in \mathcal{L} \setminus F \right]
F = \text{``nearest face"}
= \mathbb{P} \left[\hat \theta \text{ is a corner} \right]
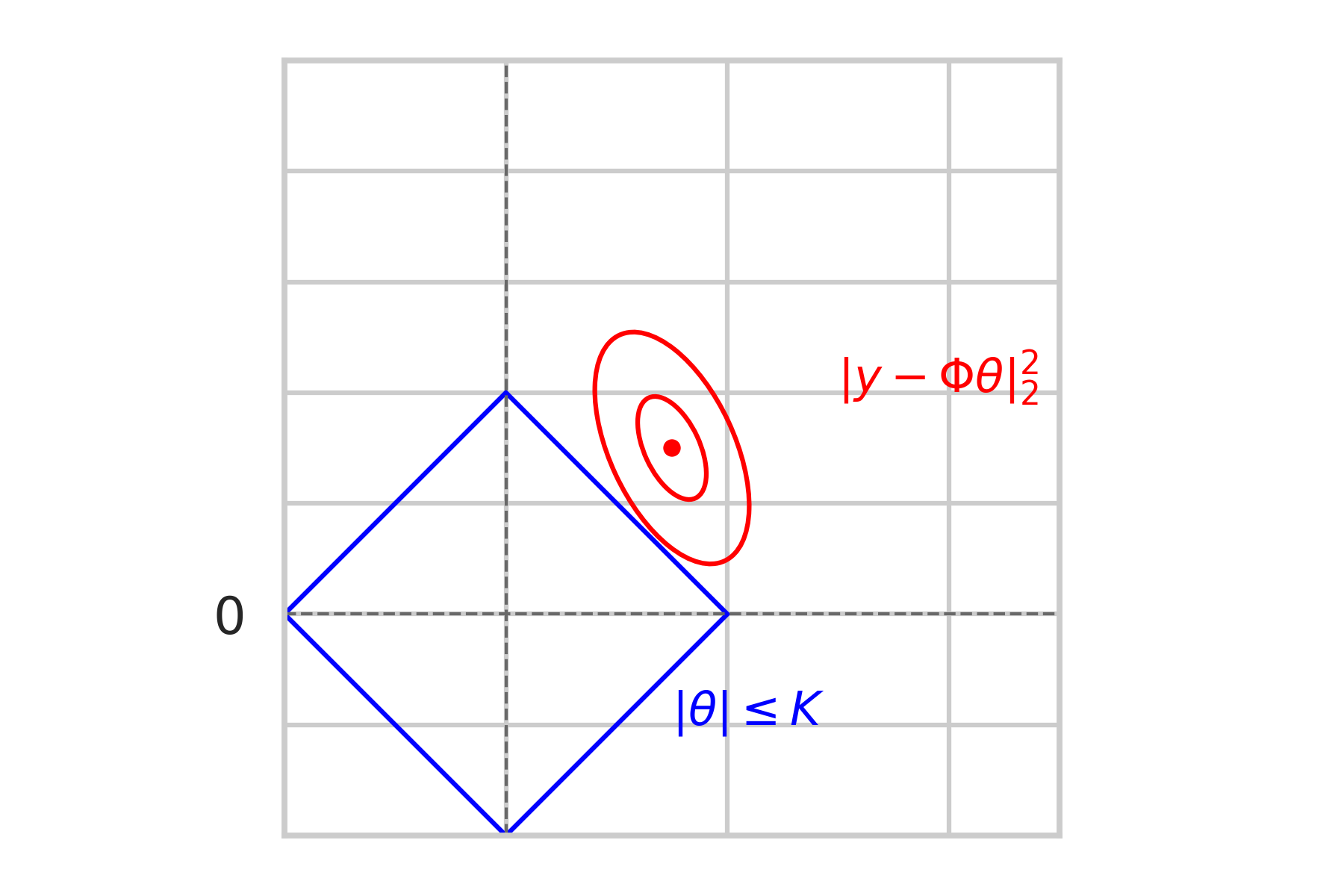
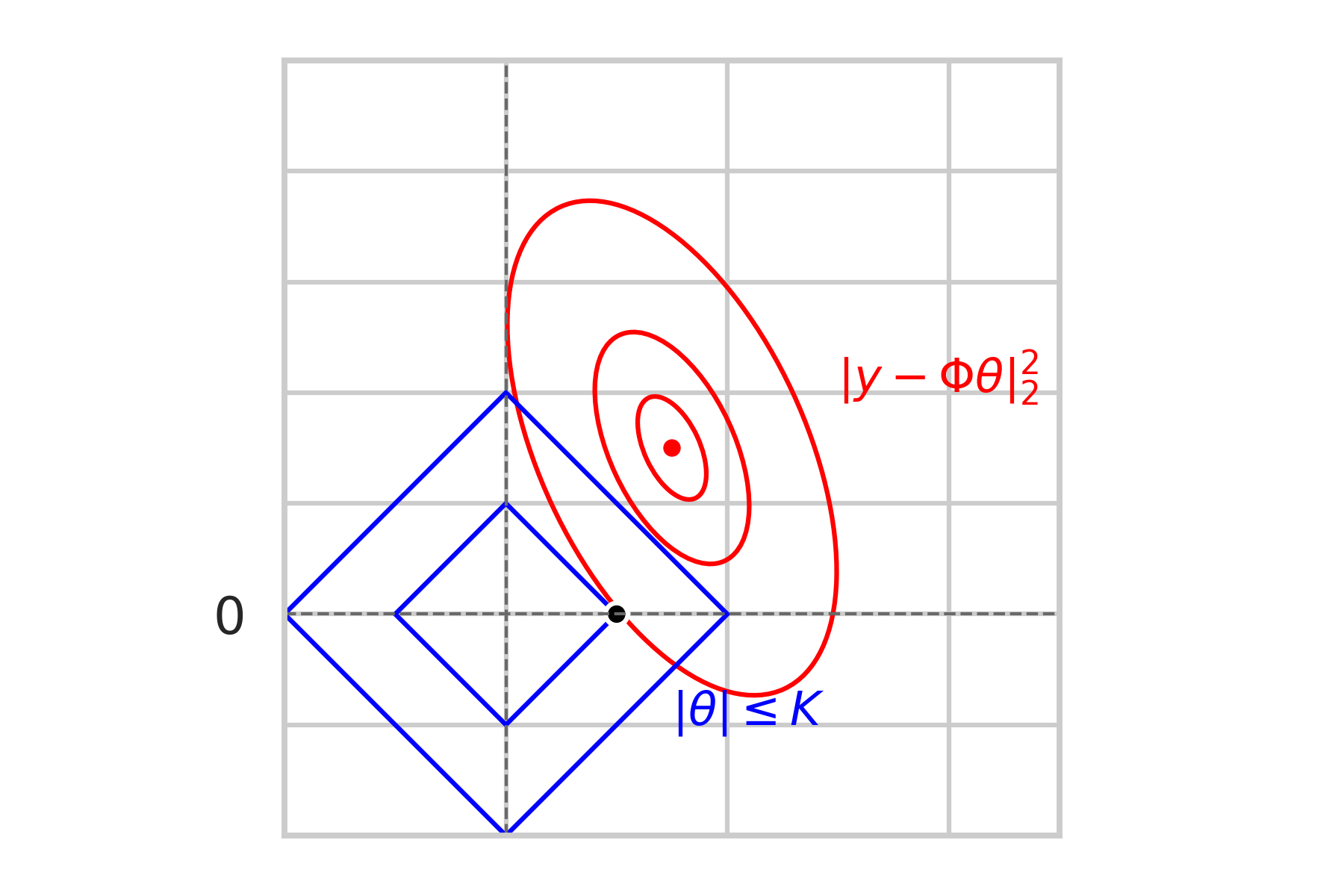
\bullet \hspace{2mm} \text{We could also adjust } K
\textbf{Sparcity-inducing effect}
\text{One-dimensional problem:}
\min\limits_{\theta\in \mathbb{R}} \hspace{1mm} \frac{1}{2} ( y - \theta )^2 + \lambda |\theta|
=: F(\theta)
\bullet \hspace{2mm} F \text{ is strongly convex } \Rightarrow \text{ unique minimizer}
\theta_\lambda^*(y) \text{ min. } F \hspace{2mm} \Leftrightarrow \hspace{2mm}\partial_{-}F(\theta^*) \leq 0 \leq \partial_{+} F(\theta^*)
\partial_{-}F(0) = -\lambda - y \leq 0\\
\partial_{+}F(0) = \hspace{3mm} \lambda - y \geq 0
\partial F(\theta) = (\theta - y) + \lambda \frac{\theta}{|\theta|}
\bullet \hspace{2mm} \theta^* = 0 \hspace{2mm}?
F(\theta) = \frac{1}{2} ( y - \theta )^2 + \lambda |\theta|
\text{Finding } \theta^* =\theta_\lambda^*(y):
\Rightarrow
\Leftrightarrow
\lambda \geq |y|
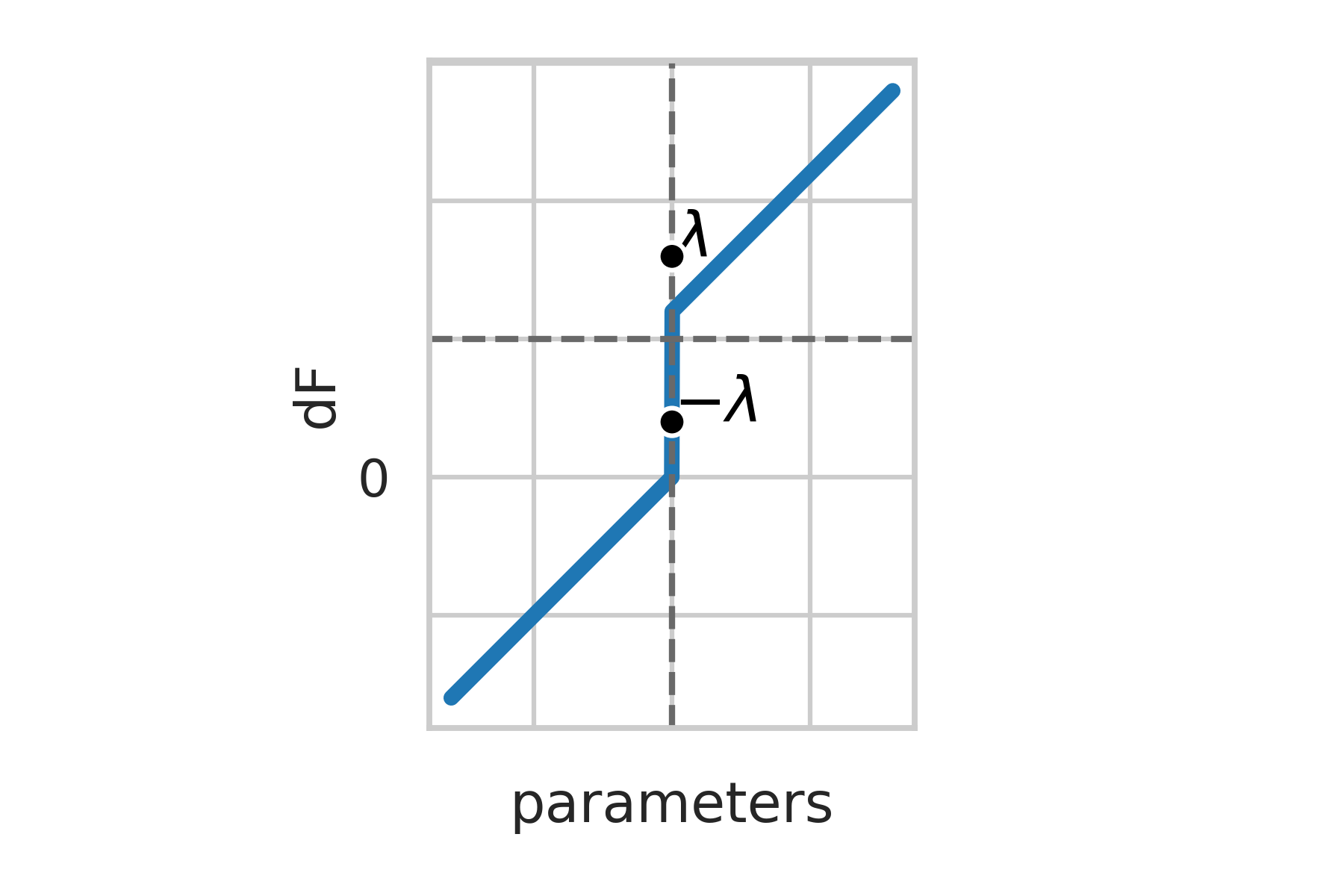
\bullet \hspace{2mm} \theta^* \neq 0
\partial F(\theta^*) = \theta^* - (y - \lambda \text{sign}(\theta^*))
= 0
\Rightarrow
\theta^* = y - \lambda \text{sign}(\theta^*)
\Rightarrow
\theta^* = (y - \lambda), \hspace{2mm} \text{if } \hspace{2mm} y > \lambda
= (y + \lambda), \hspace{2mm} \text{if } \hspace{2mm} y < -\lambda
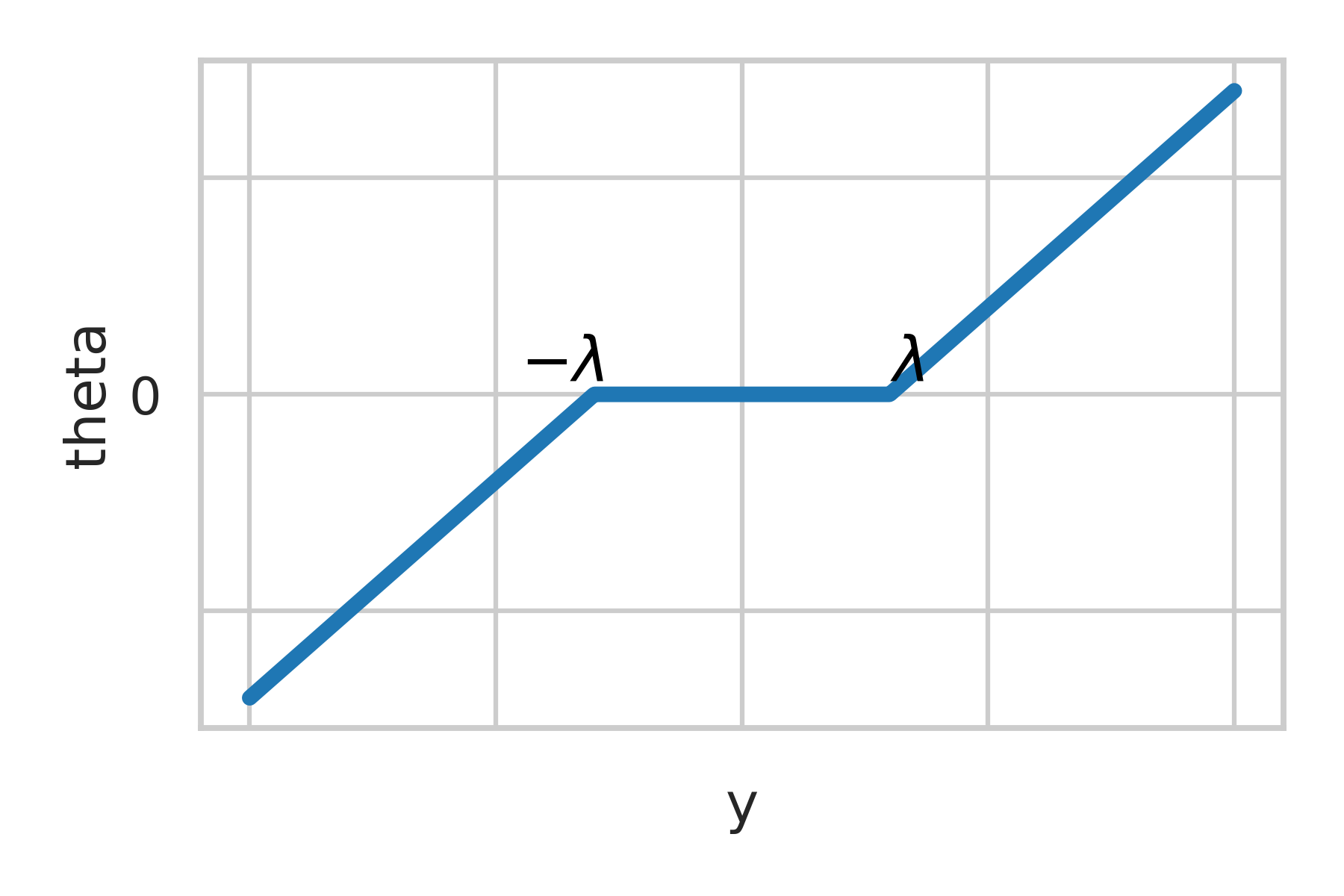
\Rightarrow
Shrinking effect
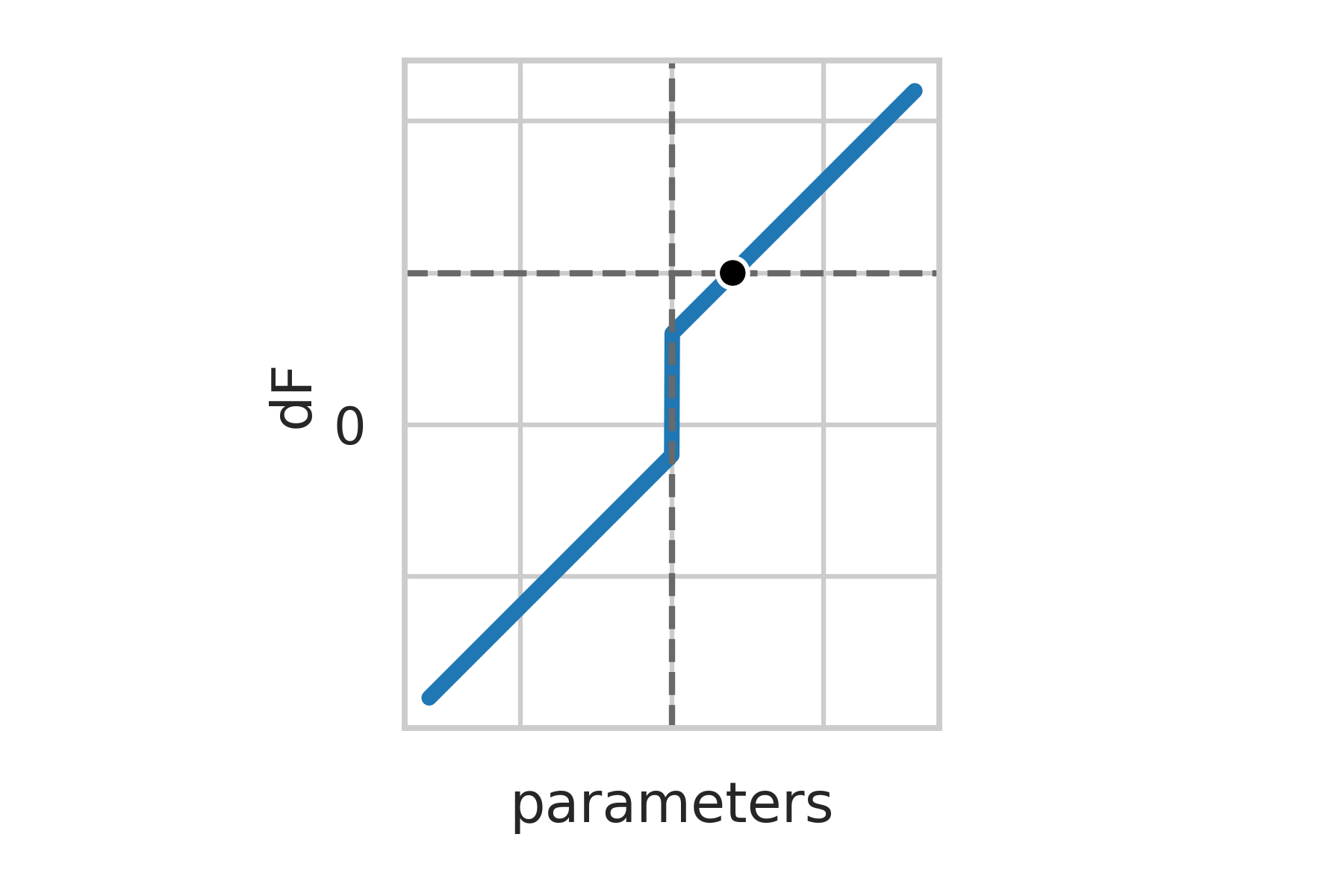
\text{Optimality conditions:}
H(\theta) = F(\theta) + \lambda \|\theta\|_1
\partial H(\theta, \Delta) = \lim\limits_{\varepsilon\rightarrow 0} \frac{1}{\varepsilon} [ H(\theta+\varepsilon \Delta) - H(\theta) ]
= F'(\theta)^T \Delta + \lambda \sum\limits_{j, \theta_j\neq 0} \text{sign}(\theta_j)\Delta_j + \lambda\sum\limits_{j, \theta_j= 0} |\Delta_j|
F'(\theta)_j + \lambda\text{sign}(\theta_j) = 0 \hspace{3mm} \forall j \in [d] \text{ s.t. } \theta_j\neq 0
|F'(\theta)_j| \leq \lambda \hspace{3mm} \forall j \in [d] \text{ s.t. } \theta_j = 0
8.3.2 Slow rates
\Omega: \mathbb{R}^d \rightarrow \mathbb{R} \hspace{2mm} \text{ - norm}
\Omega^*(z) = \sup\limits_{\Omega(\theta) \leq 1} z^T \theta \hspace{2mm} \text{ - dual norm}
\hat{\theta} \text{ minimizer for }
\frac{1}{2 n} \| y - \Phi \theta \|_2^2 + \lambda \Omega(\theta)
\bar R = \frac{1}{n} \left\|\Phi (\hat{\theta} - \theta^*)\right\|_2^2 \hspace{3mm}\text{(excess risk)}
\text{Lemma 8.4}
\text{(a) } \Omega^*(\Phi^T \varepsilon) \leq \frac{n\lambda}{2} \hspace{2mm} \Rightarrow \hspace{2mm} \Omega(\hat{\theta}) \leq 3 \Omega(\theta^*) \text{ and }
\bar R \leq 3 \lambda \Omega(\theta^*)
\text{(b) In general } \bar R \leq \frac{4}{n}\|\varepsilon\|_2^2 + 4 \lambda \Omega(\theta^*)
\text{Proof:}
\| y - \Phi \hat\theta \|_2^2 \leq \| y - \Phi \theta^* \|_2^2 + 2 n \lambda \Omega(\theta^*) - 2 n \lambda \Omega(\hat\theta)
\|\varepsilon\|_2^2 - 2 \varepsilon^T \Phi (\hat\theta - \theta^*) + \|\Phi(\hat\theta - \theta^*)\|_2^2
=
\|\Phi(\hat\theta - \theta^*)\|_2^2 \leq 2 \varepsilon^T \Phi (\hat\theta - \theta^*) + 2 n \lambda \Omega(\theta^*) - 2 n \lambda \Omega(\hat\theta)
\Rightarrow
\text{(a) If } \Omega^*(\Phi^T \varepsilon) \leq \frac{n\lambda}{2}
n \bar R \leq 2 \varepsilon^T \Phi (\hat\theta - \theta^*) + 2 n \lambda \Omega(\theta^*) - 2 n \lambda \Omega(\hat\theta)
\times \frac{\Omega(\hat\theta - \theta^*)}{\Omega(\hat\theta - \theta^*)}
\leq \Omega^* (\Phi^T \varepsilon) \Omega(\hat\theta - \theta^*) \leq \frac{n\lambda}{2} \Omega(\hat\theta - \theta^*)
\leq n \lambda \Omega(\hat\theta - \theta^*) + 2 n \lambda \Omega(\theta^*) - 2 n \lambda \Omega(\hat\theta)
\leq 3 n \lambda \Omega(\theta^*) - n \lambda \Omega(\hat\theta)
\|\Phi(\hat\theta - \theta^*)\|_2^2 \leq 2 \|\varepsilon\|_2 \|\Phi (\hat\theta - \theta^*)\|_2 + 2 n \lambda \Omega(\theta^*)
\text{(b) For the general case}
\|\Phi(\hat\theta - \theta^*)\|_2^2 \leq \frac{1}{2} \|\Phi(\hat\theta - \theta^*)\|_2^2 + 2 \|\varepsilon\|_2^2 + 2 n \lambda \Omega(\theta^*)
\Rightarrow
2 a b \leq \frac{a^2}{2} + 2 b^2
\text{Proposition 8.3 (Lasso - slow rate)}
\text{Assume } y = \Phi \theta^* + \varepsilon, \text{ with } \varepsilon \in \mathbb{R}^n \sim \mathcal{N}(0, \sigma^2 I)
\text{Then for } \lambda = 4\sigma \sqrt{ \frac{\log (d n)}{n} } \sqrt{\|\hat\Sigma\|_{\infty}}
\mathbb{E} [ \bar R ] \leq 28 \sigma \sqrt{ \frac{\log (d n)}{n} } \sqrt{\|\hat\Sigma\|_{\infty}} \|\theta^*\|_1 + \frac{24}{n} \sigma^2
\text{Proof:}
\mathbb{P} \left( \|\Phi^T \varepsilon \|_\infty > \frac{n \lambda}{2} \right) \leq \sum\limits_{j=1}^d \mathbb{P} \left( |\Phi^T \varepsilon |_j > \frac{n \lambda}{2} \right)
\leq 2 d \exp{(-\frac{n \lambda^2}{8\sigma \|\hat \Sigma\|_\infty})} =: \delta
\bullet \hspace{2mm} \bar R\leq 3 \lambda \|\theta^*\|_1, \text{ with probability } 1 -\delta
= \mathcal{A}
\mathbb{E} [\bar R] \leq 3\lambda \|\theta^*\|_1 + \mathbb{E}[ 1_\mathcal{A} \bar R ]
\leq 3\lambda \|\theta^*\|_1 + \mathbb{E}\left[ 1_\mathcal{A} \left(\frac{4}{n}\|\varepsilon\|_2^2 + 4 \lambda \|\theta^*\|_1\right) \right]
\leq 7\lambda \|\theta^*\|_1 + \frac{4}{n} \mathbb{P}(\mathcal{A})^{\frac{1}{2}} \left(\mathbb{E}\left[ \|\varepsilon\|_2^4 \right]\right)^{\frac{1}{2}}
\text{Since }\varepsilon \text{ is Gaussian, then } \left(\mathbb{E}\left[ \|\varepsilon\|_2^4 \right]\right)^{\frac{1}{2}} \leq 3 n \sigma^2
\mathbb{E} [\bar R] \leq 7\lambda \|\theta^*\|_1 + 24 d \sigma^2 \exp{\left( -\frac{n \lambda^2}{16 \sigma^2 \|\hat\Sigma\|_\infty} \right)}
\text{From our choice of }\lambda: \frac{n \lambda^2}{16 \sigma^2 \|\hat\Sigma\|_\infty} = \log(d n)
\mathbb{E} [\bar R] \leq 7\lambda \|\theta^*\|_1 + 24 \frac{\sigma^2}{n}
\leq 28 \sigma \sqrt{ \frac{\log (d n)}{n} } \sqrt{\|\hat\Sigma\|_{\infty}} \|\theta^*\|_1 + 24 \frac{\sigma^2}{n}
8.3.3 Fast rates
\text{Lemma 8.5:}
\Delta := \hat \theta - \theta^*
A := \text{supp}(\theta*) = \{j: \theta^*_j \neq 0\}
\|\Phi^T \varepsilon\|_\infty \leq \frac{n\lambda}{2} \hspace{2mm} \Rightarrow \hspace{2mm} \|\Delta_{A^C}\|_1 \leq 3 \|\Delta_{A}\|_1 \text{ and }
\bar R \leq 3 \lambda \|\Delta_A\|_1
\text{Proof:}
\|\Phi\Delta\|_2^2 \leq 2 \varepsilon^T \Phi \Delta + 2 n \lambda \|\theta^*\|_1 - 2 n \lambda \|\hat\theta\|_1
\leq n \lambda \|\Delta\|_1 + 2 n \lambda ( \|\theta^*\|_1 - \|\hat\theta\|_1)
\|\theta^*\|_1 - \|\hat\theta\|_1 = \|\theta^*_A\|_1 - \|\theta^* + \Delta\|_1
= \|\theta^*_A\|_1 - \|(\theta^* + \Delta)_A\|_1 - \|\Delta_{A^C}\|_1
\leq \|\Delta_A\|_1 - \|\Delta_{A^C}\|_1
\Rightarrow
\bar R \leq \lambda \|\Delta\|_1 + 2 \lambda ( \|\Delta_A\|_1 - \|\Delta_{A^C}\|_1)
\leq 3\lambda \|\Delta_A\|_1 - \lambda \|\Delta_{A^C}\|_1
\text{Assumption for fast rate:}
\frac{1}{n}\|\Phi\Delta\|_2^2 \geq \kappa \|\Delta_A\|_2^2
\text{for all }\Delta \text{ such that } \|\Delta_{A^C}\|_1 \leq 3 \|\Delta_A\|_1
(8.5)
\text{Proposition 8.4 (Lasso - Fast rate)}
\text{Assume } y = \Phi \theta^* + \varepsilon, \text{ with } \varepsilon \in \mathbb{R}^n \sim \mathcal{N}(0, \sigma^2 I)
\text{Then for } \lambda = 4\sigma \sqrt{ \frac{\log (d n)}{n} } \sqrt{\|\hat\Sigma\|_{\infty}}
\mathbb{E} [ \bar R ] \leq \dfrac{144 |A| \sigma^2 \|\hat\Sigma\|_\infty}{\kappa} \dfrac{\log(d n)}{n} + \dfrac{24}{n} \sigma^2
\text{and assuming (8.5)}
+ \dfrac{32}{d n^2} \|\theta^*\|_1 \sigma \sqrt{ \dfrac{\log(d n)}{n} \|\hat\Sigma\|_\infty }
\text{Proof:}
\|\Delta_A\|_1 \leq |A|^{\frac{1}{2}} \|\Delta_A\|_2 \leq \frac{1}{\sqrt{n\kappa}}|A|^{\frac{1}{2}} \|\Phi \Delta\|_2
\text{When } \|\Phi^T \varepsilon\|_\infty \leq \frac{n\lambda}{2}
\leq \frac{1}{\sqrt{n\kappa}}|A|^{\frac{1}{2}} \sqrt{ 3 n \lambda \|\Delta_A\|_1 }
\Rightarrow
\|\Delta_A\|_1 \leq \frac{3 \lambda |A|}{\kappa}
\bar R \leq 3\lambda \|\Delta_A\|_1 \leq \frac{9 |A| \lambda^2}{\kappa}
(8.5)
\text{Lemma 8.5:}
\Rightarrow
\text{Lemma 8.5:}
\mathbb{E} [\bar R] \leq \dfrac{9 |A| \lambda^2}{\kappa} + \mathbb{E}\left[ 1_\mathcal{A} \left(\frac{4}{n}\|\varepsilon\|_2^2 + 4 \lambda \|\theta^*\|_1\right) \right]
\leq \frac{24 \sigma^2}{n}
\leq \dfrac{9 |A| \lambda^2}{\kappa} + \dfrac{24 \sigma^2}{n} + 4 \mathbb{P}(\mathcal{A}) \lambda \|\theta^*\|_1
\leq \dfrac{9 |A| \lambda^2}{\kappa} + \dfrac{24 \sigma^2}{n} + 8 d \lambda \|\theta^*\|_1\exp{\left( -\frac{n \lambda^2}{8 \sigma^2 \|\hat\Sigma\|_\infty} \right)}
\leq \dfrac{9 |A| \lambda^2}{\kappa} + \dfrac{24 \sigma^2}{n} + \dfrac{8 \lambda \|\theta^*\|_1}{d n^2}
= 2 \log{(d n)}
8.3.4 Zoo of conditions
\text{Restricted eigenvalue property (REP):}
\inf\limits_{|A|\leq k} \inf\limits_{\|\Delta_{A^C}\|_1 \leq \|\Delta_A\|_1} \dfrac{\|\Phi \Delta\|_2^2}{n \|\Delta_A\|_2^2} \geq \kappa > 0
\bullet \hspace{2mm} \text{equivalent to assumption (8.5).}
\text{Mutual incoherence condition:}
\sup\limits_{i\neq j} |\hat\Sigma_{i,j}| \leq \frac{1}{14 k} \min\limits_{j\in [d]} \hat\Sigma_{j,j}
\bullet \hspace{2mm} \text{Simpler to check, but weaker than REP}
\text{Restricted isometry property}
\text{All eigenvalues of submatrices of }\hat\Sigma\text{ of size less than }2 k,
\text{are between }1-\delta\text{ and }\delta.
\text{Theorem 8.1 (Gaussian design)}
\text{If }\varphi(x)\text{ is Gaussian with zero mean and covariance }\Sigma.
\text{Then, with prob. greater than } \left( 1 - \frac{e^{-\frac{n}{32}}}{1 - e^{-\frac{n}{32}}} \right) \text{ REP holds}
\text{with }\kappa = \frac{c_1}{2} \lambda_{\min}(\Sigma)\text{ as soon as}
\dfrac{k \log(d)}{n} \leq \dfrac{c_1}{8 c_2} \dfrac{\lambda_{\min} (\Sigma)}{\|\Sigma\|_\infty}, \hspace{4mm}\text{ with }c_1 = \frac{1}{8}\text{ and }c_2 = 50.
\text{Algorithms}
\text{Iterative hard-thresholding:}
\theta_t = \argmin\limits_{\theta\in \mathbb{R}^d} F(\theta_{t-1}) + F'(\theta_{t-1})^T (\theta - \theta_{t-1}) + \frac{L}{2}\|\theta - \theta_{t-1}\|_2^2 + \lambda\|\theta\|_1
\text{with } L = \lambda_{\max} \left( \frac{1}{n} \Phi^T\Phi \right)
\Rightarrow
(\theta_t)_j = \max\{ |(\eta_t)_j| - \lambda, 0 \} \text{sign}((\eta_t)_j)
\eta_t = \theta_{t-1} - \frac{1}{L} F'(\theta_{t-1})
\text{Proximal method recursion:}
\eta\text{-trick:}
|\theta_j| = \inf\limits_{\eta_j>0} \frac{\theta_j^2}{2 \eta_j} + \frac{\eta_j}{2}
\text{Approximate }\|\cdot\|_1 \text{using}
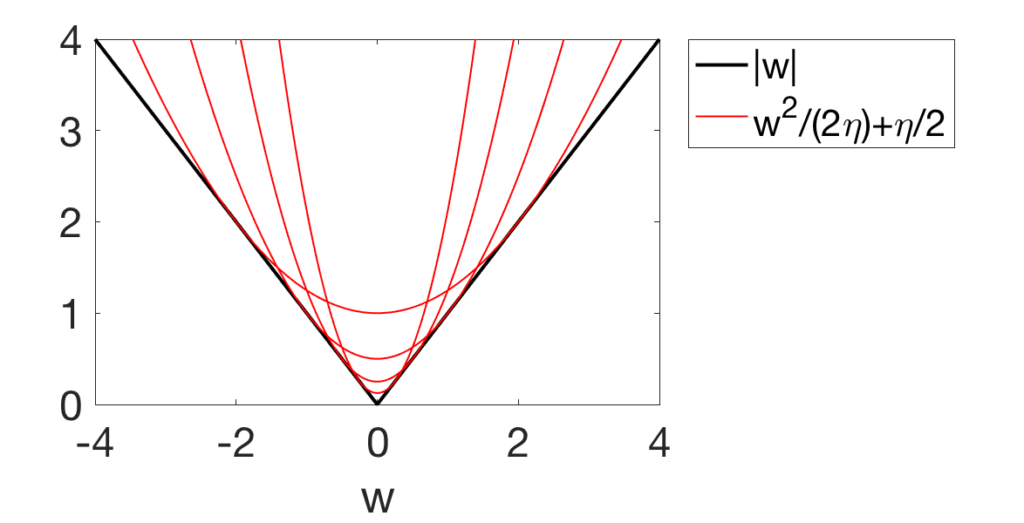
\text{(L)} = \inf\limits_{\eta\in\mathbb{R}^d_{+}} \inf\limits_{\theta\in\mathbb{R}^d} \frac{1}{2 n} \|y - \Phi\theta\|_2^2 +
\frac{\lambda}{2} \sum\limits_{j=1}^d \frac{\theta_j^2}{2 \eta_j} + \frac{\lambda}{2} \sum\limits_{j=1}^d \eta_j
\bullet \hspace{2mm} \text{alternated optimization}
Copy of ERM part 2
By Daniel Yukimura
Copy of ERM part 2
- 357



