Aspirin
and
Potential Outcomes
ICS212
Three slides based on Rubin Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies
How would you read each of the expressions in this image from one of the first readings of the semester?
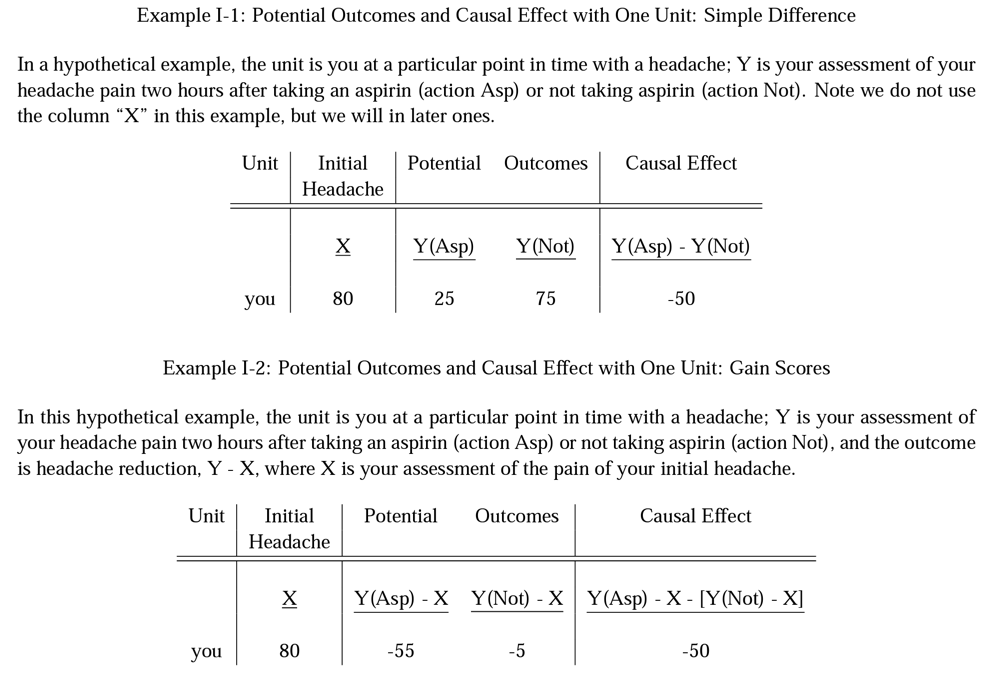
Y(Asp) is how my head feels two hours after taking an aspirin. Y(Not) is how my head feels two hours after not taking an aspirin.
The causal effect is the difference between how I feel two hours after taking an aspirin and two hours after not taking an aspirin.
The outcome is how my head feels two hours after taking an aspirin as compared to how it felt before I took the aspirin.
The causal effect is the difference between the change in my headache after an aspirin and the change in my headache after no aspirin.
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin. P 4
ICS212 Fall 2022

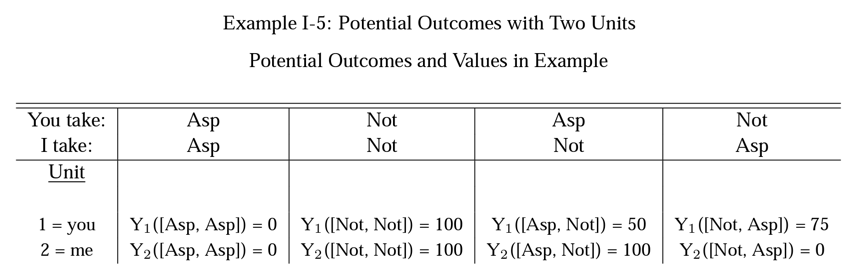
This table represents an experiment in which you and I both have headaches. Explain what the selected part of the table means.
The column Asp Not corresponds to you taking an aspirin and me not taking an aspirin.
The subscripts 1 and 2 refer to your and my, respectively, outcomes - how our heads feel at the end of two hours.
In the square brackets we have the treatments - you took an aspirin and I did not.
The numbers indicate the "value" of each of our headaches.
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin. P 6
ICS212 Fall 2022

This table represents an experiment in which you and I both have headaches. How does the information in the green box indicate that SUTVA is violated?
The treatment effect for you when I take an aspirin is = Y1([Asp,Asp]) - Y1([Not,Asp]) = 0 - 75 = -75
But the treatment effect for you when I do not take an aspirin is
= Y1([Asp,Not]) - Y1([Not,Not]) = 50 - 100 = -50
The causal effect for you depends in some way on whether I get treatment or control. That violates first part of SUTVA.

Make up a story that might explain this peculiar situation.
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin. P 6
ICS212 Fall 2022

Aspirin
By Dan Ryan
Aspirin
Three slides based on Rubin Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies
- 304



