Logo, course, and module name: INF1339 Computational Thinking session on "Logic"

Logic

NOTES from google drive

Logic II

Logo, course, and module name: INF313 Computational Reasoning session called "Logic"

STOP+THINK.
How many rows in the truth table for this expression? 

VW!XY || !VWZ || VWYZ || VW!XYZ

Solution

5031

STOP+THINK.
How many rows in the truth table for this expression? 

VW!XY || !VWZ || VWYZ || VW!XYZ

Count the variables: V, W, X, Y, and Z - five total.
Therefore we need 25=32 rows.

Back

Motivation

you want to build a number displaying machine

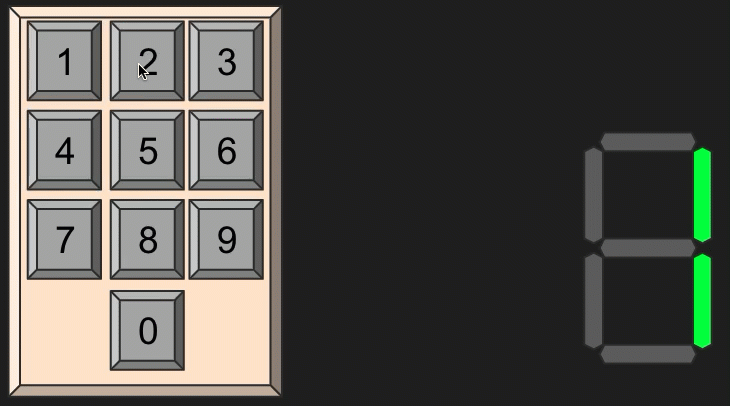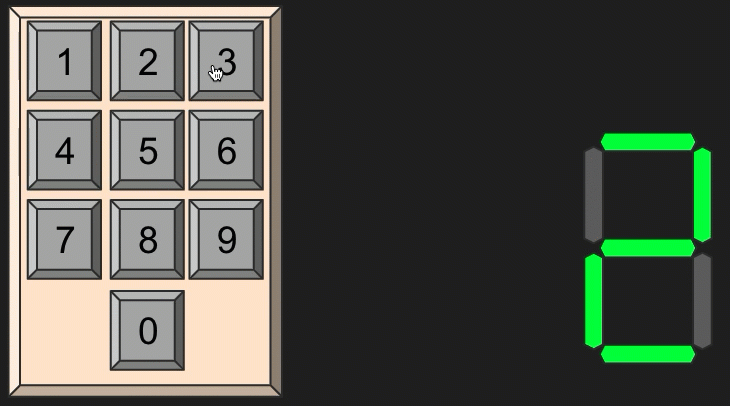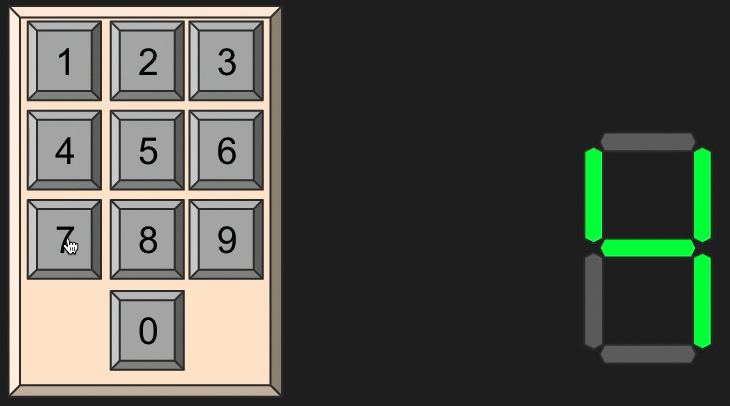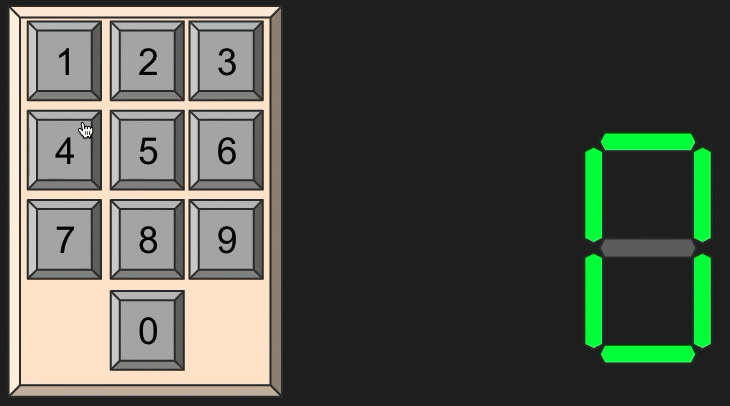
Tutorial

Prep

  • y = f(x)
  • CSS classes
  • another page element property (classname)
  • JavaScript "switch" 

We have set up a shell with some HTML, CSS, and JS. Here's what happened behind the scenes:

Create 10 buttons in the <div> each of which sends a single digit to a function called "display(x)"

Create a <div> ("division") element to contain our button pad

Add <br /> ("line break") tags to create "line breaks" so we see three buttons per line

Create a table in HTML with 5 rows and 3 columns that we can use for the seven segment display.

Give the seven table cells that will be part of the 7 segment display the ids A through G.

Give the table cells A, G, and D the class "horizontal" and cells B, C, E, F the class "vertical" so that we can use CSS to style them

Instructions 1

Create the classes vertical and horizontal in CSS

.vertical {
           width: 20;
           height: 60;
           background-color: red;
}

.horizontal

{
           width: 60;
           height: 20;
           background-color: red;
}

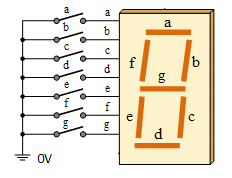
off on on off off off off

on off on on off on on

on on on on on on on

Think Slowly
Start Simply

Can we design a digital electronic machine to do this?

Imperfect Analogy

ANALOG - CONTINUOUS

DIGITAL - DISCRETE

ANALOG - CONTINUOUS

DIGITAL - DISCRETE

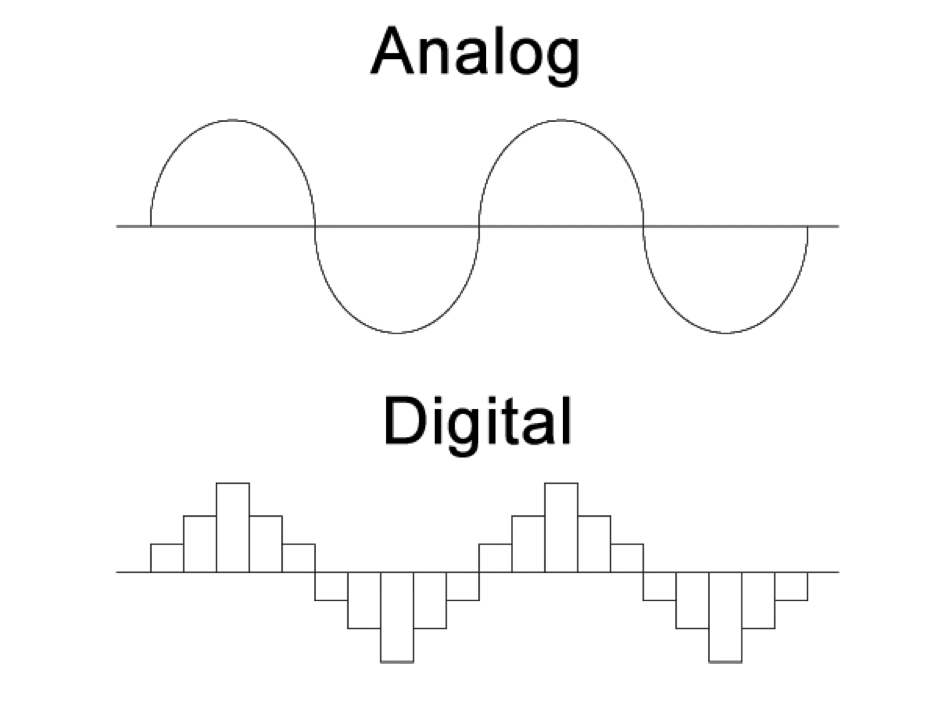
analog

digital

input 

output 

4 input bits

4 input bits

5 output bits

push button switches

Tools We Already Have

  • Binary output from each key

?

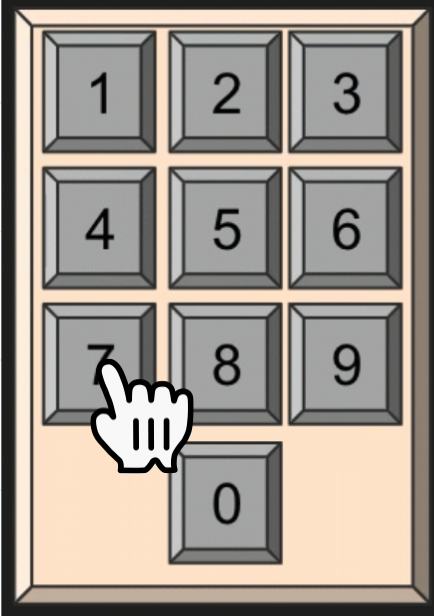
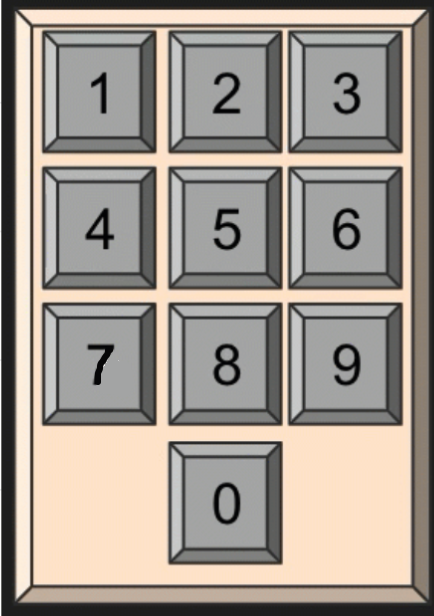
Agenda

  • Logic
  • Circuits

Review

Review

Statement: sentence that can be true or false

Logical operators: and/or/not

Logical variables: letters that stand for statements

Logical expression: combination of logical variables and operators

Truth table: table showing all possible "inputs" and corresponding outputs for a logical expression

Logical values: true/false

Four "laws"

  DeMorgan's (2)

  Distributive

  Double negation

Alternative notations

LOGIC 101

My name is Dan.

My name is Dan.

value = TRUE

value = FALSE

A = it is sunny out

A?

A = it is sunny out

A?

A is a logical variable. A name that stands for a statement or condition that can be true or false.

A LOGICAL VARIABLE CAN TAKE ON ONE OF TWO LOGICAL VALUES

TRUE

FALSE

1

0

LOGICAL VARIABLES can be combined

with LOGICAL OPERATORS

such as AND, OR, and NOT

to form LOGICAL EXPRESSIONS

which also can only be TRUE or FALSE

LOGICAL EXPRESSIONS

for example

A = "my name is Dan."

B = "I am in Toronto."

C = "I am a dog."

D = A and B
E = A and C
F = A or B
G = not C
H = B and not C
I = not A or not C

TRUE

TRUE

TRUE

TRUE

TRUE

FALSE

LOGICAL OPERATORS

  • "Binary" Operators (connecting two values)
    • AND
    • OR
  • "Unary" Operator (works on just one value)
    • NOT

Alternative Notations

A and B also written   AB,   A∧B,   A·B

A or B also written   A+B,   A∨B

not A also written   ~A,   !A,   ¬A,   Ā

Definitions I

W is true if both A, B are true

W is true when A is false, false when A is true

W = A or B

W = A and B

W is true if either or both A,B truee

W = not A

Boolean Algebra: the "math" of logic

  • akin to multiplication
  • AB, A∧B, A·B
  • 1 or TRUE is identity
    • X AND TRUE = X
    • X·1=X for any X

Only two "numbers": 0 and 1

Three "operations":

AND

  • akin to addition
  • A+B, A∨B
  • 0 or FALSE is identity element
    • X or FALSE = X
    • X+0=X
  • akin to negation
  • ~A, !A, ¬A, Ā
  • not 0 = 1, not 1 = 0

OR

NOT

Boolean Algebra: the "math" of logic

AND takes precendence over OR

AB + C

means "A and B ... or C"

not "A and ... B or C"

but use parentheses to say otherwise

A(B + C)

means "A and ... B or C"

Boolean Algebra: the "math" of logic

AND "distributes" over OR

A(B + C) = AB + AC

Boolean Algebra: the "math" of logic

common vars can be "factored out: of ORs

AB + AC = A(B + C)

Boolean Algebra: the "math" of logic

Since 1/0 are exhaustive

A + !A = TRUE

Since 1/0 are mutually exclusive

A · !A = FALSE

Boolean Algebra: the "math" of logic

Summary so far

A + !A = TRUE

A · !A = FALSE

AB + AC = A(B + C)

A(B + C) = AB + AC

X·1 = X for any X

X+0 = X for any X

TRUTH TABLES

A logical expression is DEFINED by its truth table which shows its value for every possible combination of inputs

TRUTH TABLES

A truth table is simply a listing of all possible combinations for an expression along with the value of the expression for each combination.

Suppose an expression includes three variables A, B, and C.

A can be true or false

B can be true or false

C can be true or false

B can be true or false

C can be true or false

C can be true or false

C can be true or false

1

0

11

10

01

00

111

110

101

100

011

010

001

000

A

C

B

exp

TRUTH TABLES

A truth table is simply a listing of all possible combinations for an expression along with the value of the expression for each combination.

Suppose an expression includes three variables A, B, and C.

0          0          1

0          0          0

0          1          0

0          1          1

1          0          0

1          0          1

1          1          0

1          1          1

A

C

B

exp

"expression" - we'll put the value of the expression for each input combination here

TRUTH TABLES

A B A+B
1 1 1
1 0 1
0 1 1
0 0 0

row for each

input combination

row for each

input combination

column
for each

variable

column
for "output"

TRUTH TABLES

A B A+B
1 1 1
1 0 1
0 1 1
0 0 0

all the 1's for the first varible

{

all the 0's for the first varible

{

A B C
1 1 1
1 1 0
1 0 1
1 0 0
0 1 1
0 1 0
0 0 1
0 0 0
A B C D
1 1 1 1
1 1 1 0
1 1 0 1
1 1 0 0
1 0 1 1
1 0 1 0
1 0 0 1
1 0 0 0
0 1 1 1
0 1 1 0
0 1 0 1
0 1 0 0
0 0 1 1
0 0 1 0
0 0 0 1
0 0 0 0
A
1
0
A B
1 1
1 0
0 1
0 0
A B C
1 1 1
1 1 0
1 0 1
1 0 0
0 1 1
0 1 0
0 0 1
0 0 0
A B C D
1 1 1 1
1 1 1 0
1 1 0 1
1 1 0 0
1 0 1 1
1 0 1 0
1 0 0 1
1 0 0 0
0 1 1 1
0 1 1 0
0 1 0 1
0 1 0 0
0 0 1 1
0 0 1 0
0 0 0 1
0 0 0 0

Definitions II

A B AB
1 1 1
1 0 0
0 1 0
0 0 0

AND

A B A+B
1 1 1
1 0 1
0 1 1
0 0 0

OR

A !A
1 0
0 1

NOT

Example: Build Truth Table for !A + B

A

B

1

1

0

0

1

0

1

0

!A

!A+B

1

B

1

0

1

0

0

0

1

1

0

1

1

A B C !A!B + BC
1 1 1
1 1 0
1 0 1
1 0 0
0 1 1
0 1 0
0 0 1
0 0 0

Build Truth Table for !A!B + BC

1

A B C !A!B + BC
1 1 1 1
1 1 0
1 0 1
1 0 0
0 1 1 1
0 1 0
0 0 1 1
0 0 0 1

Build Truth Table for !A!B + BC

1

2

3

A B C !A!B + BC
1 1 1 1 1
1 1 0
1 0 1
1 0 0
0 1 1 1 1
0 1 0
0 0 1 1 1
0 0 0 1 1

Build Truth Table for !A!B + BC

1

2

3

4

Example: Build Truth Table for !A!B + BC

A

B

C

1

1

1

1

0

0

0

0

1

1

1

1

0

0

0

0

1

1

1

1

0

0

0

0

!A

!B

!A·!B

B·C

!A!B+BC

1

1

1

1

1

1

1

1

0

0

0

0

1

1

1

1

0

0

0

0

1

1

1

1

0

0

0

0

Boolean Algebra: the "math" of logic

AND "distributes" over OR

A(B + C) = AB + AC

A B C A and B+C AB + AC
1 1 1 1 1 1 1 1 1
1 1 0 1 1 1 1 1
1 0 1 1 1 1 1 1
1 0 0 1 0
0 1 1 1
0 1 0 1
0 0 1 1
0 0 0 0

Laws

  • DeMorgan
    • !(AB) = !A+!B
    • !(A+B) = !A!B
  • Distributive
    • A(B+C) = AB + AC
  • Double negation
    • !!A = A

Boolean Algebra: the "math" of logic

Summary so far

A + !A = TRUE

A · !A = FALSE

AB + AC = A(B + C)

A(B + C) = AB + AC

X·1 = X for any X

X+0 = X for any X

!(A+B) = !A!B

!(A · B) = !A + !B

}

}

}

}

identity elements

distributive property

mutual exclusive + exhaustive

definition of NOT

DeMorgan's Laws

Boolean Algebra: the "math" of logic

Truth table for expression can be written as

"or of ands"

where the ands are the inputs of each row a 1 in the last column

A B C EXP
1 1 1 1
1 1 0 0
1 0 1 0
1 0 0 1
0 1 1 0
0 1 0 0
0 0 1 1
0 0 0 1

1

1

1

1

1

1

0

0

0

1

1

1

0

0

0

0

Boolean Algebra: the "math" of logic

A B C EXP
1 1 1 1
1 1 0 0
1 0 1 0
1 0 0 1
0 1 1 0
0 1 0 0
0 0 1 1
0 0 0 1

1

1

1

1

+

+

+

B

A

C

1

1

1

A

!C

!B

1

0

0

C

!A

!B

1

0

0

!C

!A

!B

0

0

0

Boolean Algebra: the "math" of logic

And, finally:

Truth table for an expression can be written as an "or of ands" where the ands are the inputs of each line of the truth table that yields a 1

A B C EXP
1 1 1 1
1 1 0 0
1 0 1 0
1 0 0 1
0 1 1 0
0 1 0 0
0 0 1 1
0 0 0 1

1

1

1

1

1

1

1

1

0

0

1

0

0

0

0

0

+

+

+

+

+

+

B

A

C

A

!C

!B

C

!A

!B

!C

!A

!B

Logic and Circuits

  • logical values and electricity

  • AND, OR

  • Basic Logic Gates

  • Simple expressions and circuits

Logic 2 Storyboard

Black Boxes
for logic

Gates
controlling switches

Electricity
switches as logic

Electricity
what is a volt?

Review

Truth Tables
stepwise refinement

logic circuits

Circuit Cost
 

Expression

Equivalence
 

Logic Reduction
 

Best Solutions?
 

Electricity

but first...


"potential" (energy)

but first...

1 kg

1 m


"potential" (energy)

but first...

1 kg

1 m

9.8 joules

Electrical Potential Energy VOLTS

positive and negative electric charges are attracted to one another

-

+

potential (volts)

Electrical Potential Energy VOLTS

separating positive and negative charges increases potential

-

+

potential (volts)

Volt

+

-

3V

Logical Values + Electricity

+3 or +5 volts

0 volts

1

0

true

false

+

-

3V

Logical Operators + Switches

Logical Values + Switches

+3-5 volts

+3-5 volts

logical 0

logical 1

OPEN SWITCH

CLOSED SWITCH

For what it's worth: the usual value of digital "1" is +3-5 volts DC

AND, OR

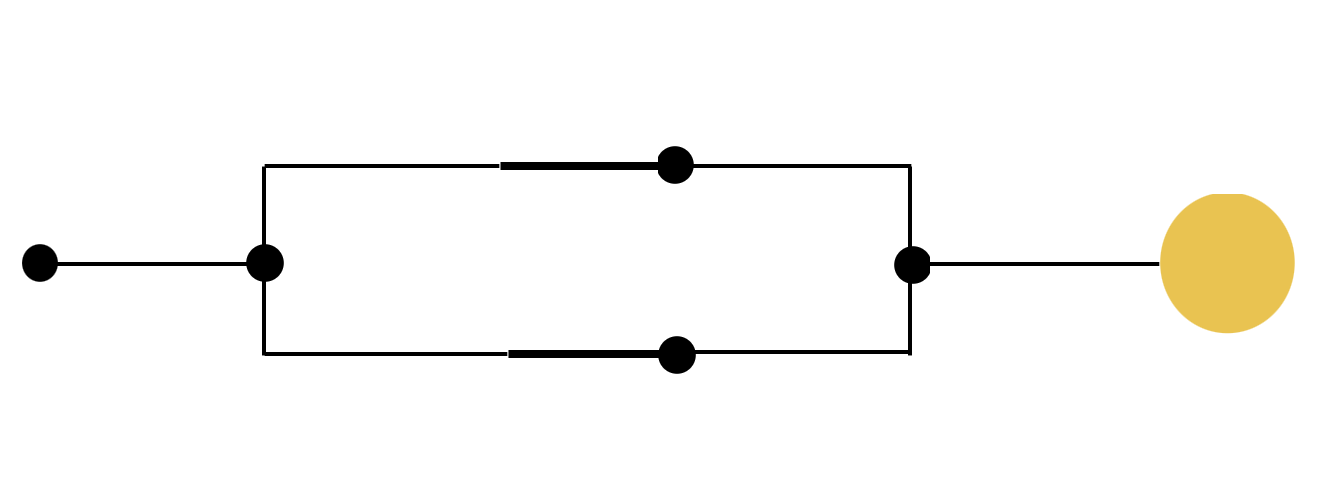
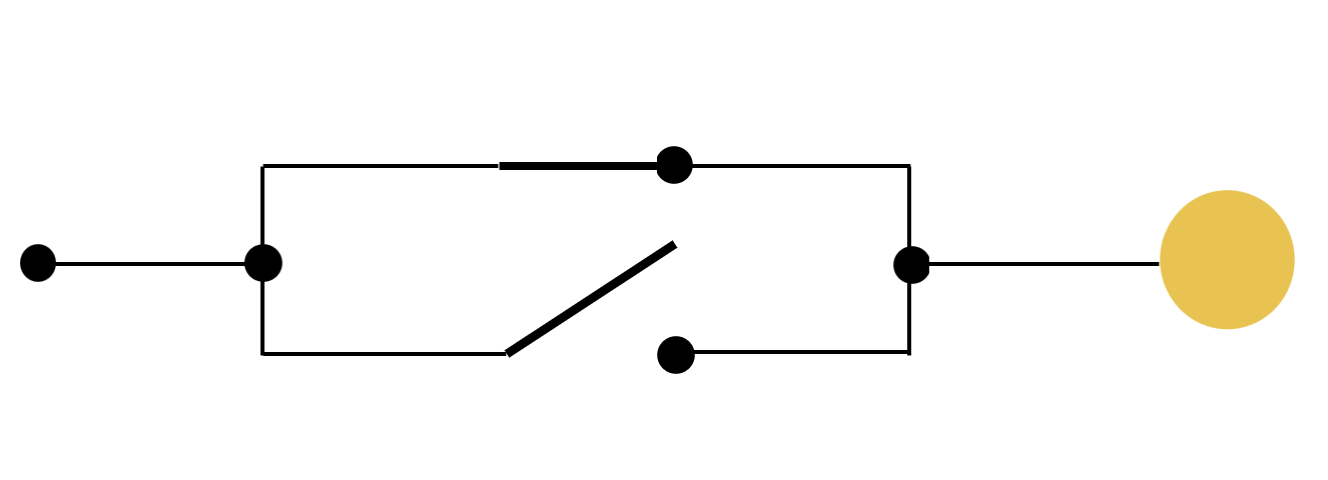
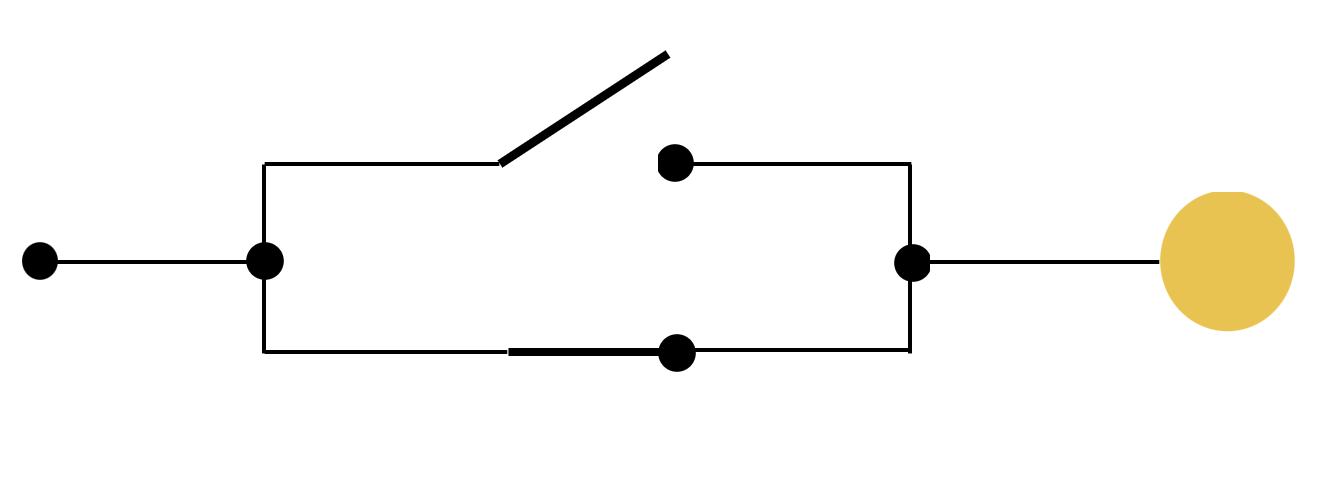
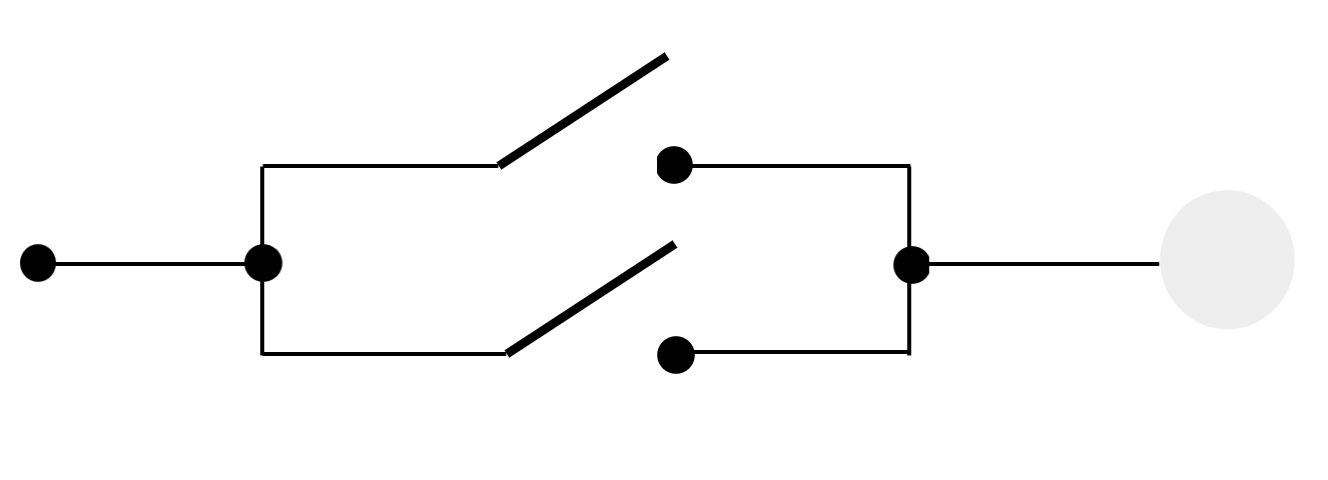
A and B

+

-

3V

A or B

Logical Operators + Switches

+

-

3V

A

B

A

B

AND as black box

A

B

3V

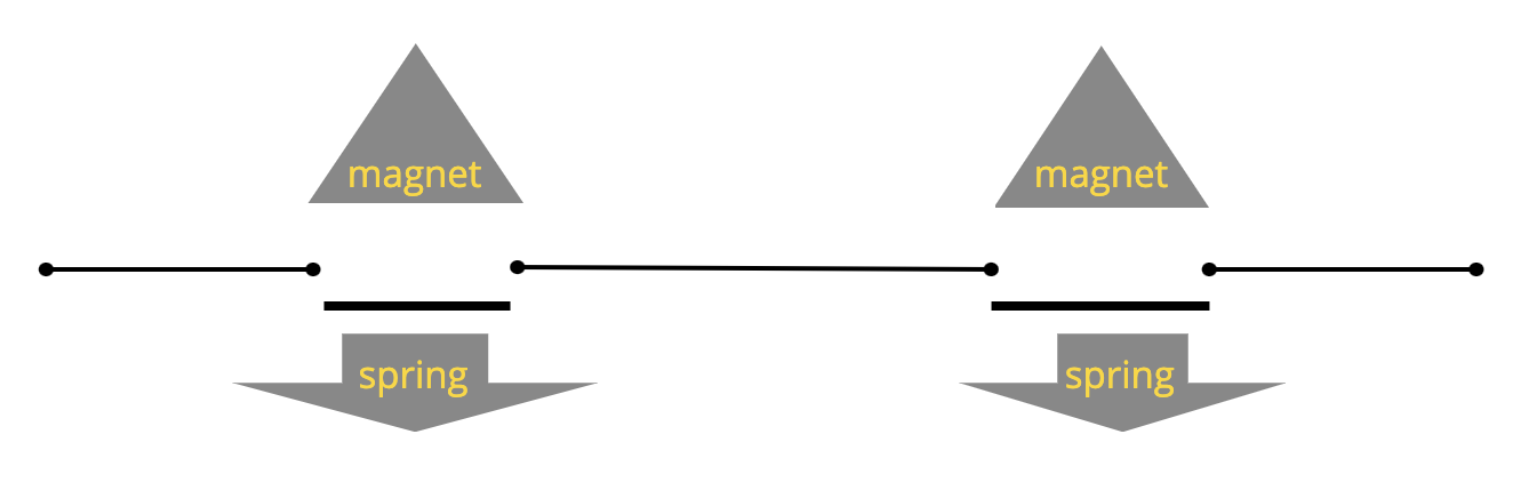
AND

magnet

spring

magnet

spring

A

B

3V

output

AND

magnet

spring

magnet

spring

A

B

3V

AND

+

-

3V

magnet

spring

magnet

spring

A

B

AND

+

-

3V

magnet

spring

magnet

spring

A

B

AND

3V

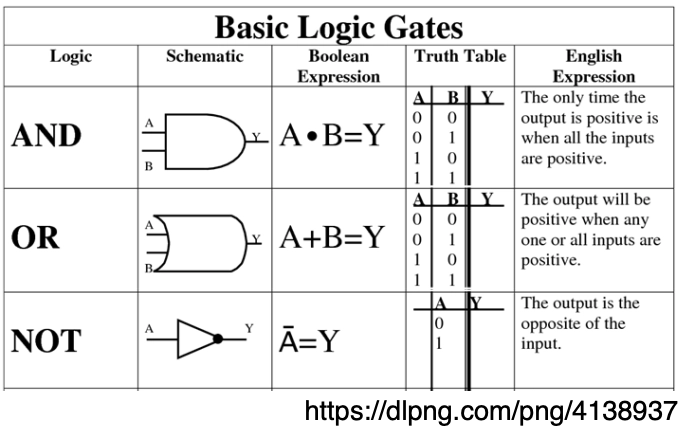
A

B

Y

A

B

Y

A

B

Y

A

B

Y

A

B

Y

OR

A

B

Y

OR

A

B

Y

OR

A

B

Y

OR

A

B

Y

OR

A

B

C

D

What is the output if the inputs are TFTF?

A

B

C

D

AB + CD

A

B

C

D

AB + CD

A

B

C

D

AB + CD

A

B

C

D

A

B

C

D

AB + CD

Simple expressions + circuits

AB + BC

A

B

C

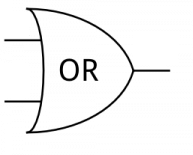
Simplifying Logic Expression = Simplifying Logic Circuits

AB + BC=B(A+C)

A

B

C

Simple expressions + circuits

C

B

A

B

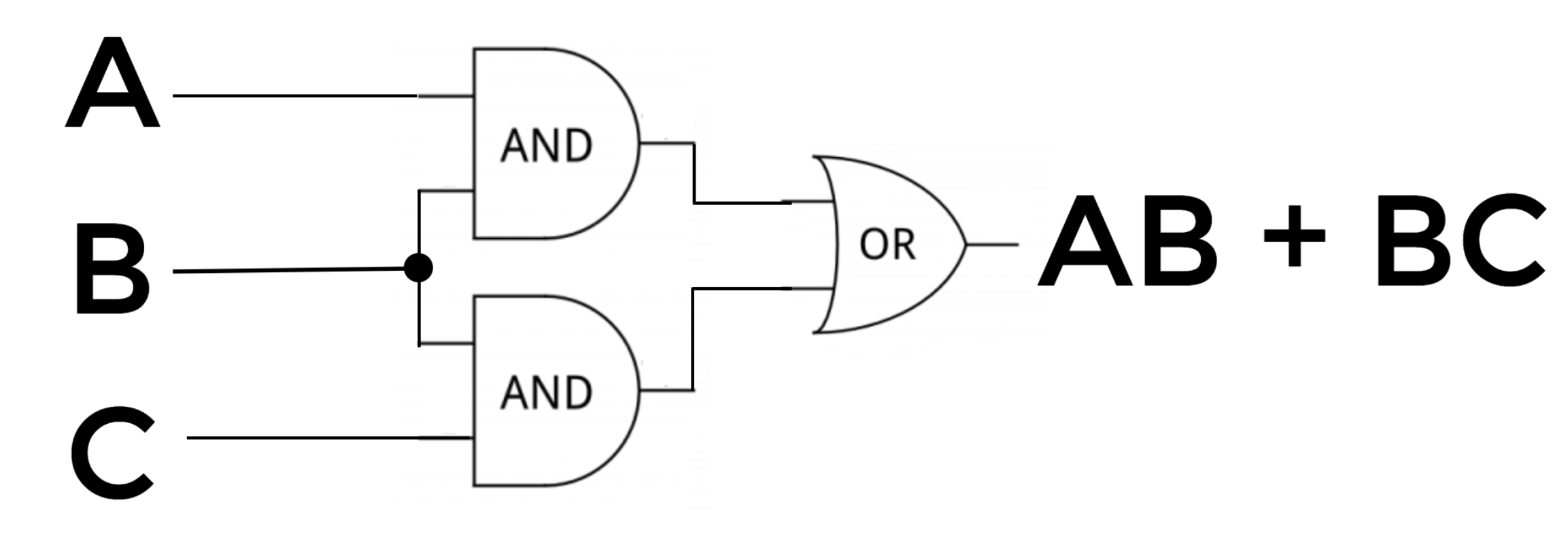
C

C

C

1

0

1

1

1

1

0

0

Simplifying Logic Expression = Simplifying Logic Circuits

AB + BC=B(A+C)

B

A

C

33% savings!

A

B

C

Simplifying Logic Expression = Simplifying Logic Circuits

AB + BC=B(A+C)

A B C AB + BC B and A+C
1 1 1  1 1  1 1  1   1
1 1 0  1 1  0 1  1   1
1 0 1  0 0  0 0  0   1
1 0 0  0 0  0 0  0   1
0 1 1  0 1  1 1  1   1
0 1 0  0 0  0 1  0   0
0 0 1  0 0  0 0  0   1
0 0 0  0 0  0 0  0   0

SKIP

Simple expressions + circuits

A
 

B
 

C

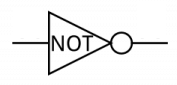
!A!B + BC

Pause

Binary
Arithmetic

1 Bit Addition

 1
+0
01

 0
+1
01

 0
+0
00

 1
+1
10

  A
 +B
 WX

1 Bit Addition

 1
+0
01

 0
+1
01

 0
+0
00

 1
+1
10

  A
 +B
 WX
A + B = W X
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

1 Bit Addition as black box with two inputs and two outputs 

  A
 +B
 WX
A + B = W X
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

A

B

W 

X 

1 Bit Addition

 1
+0
01

 0
+1
01

 0
+0
00

 1
+1
10

  A
 +B
 WX
A + B = W X
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

looks like
A and B

1 Bit Addition

A + B = W X
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

looks like
A and B

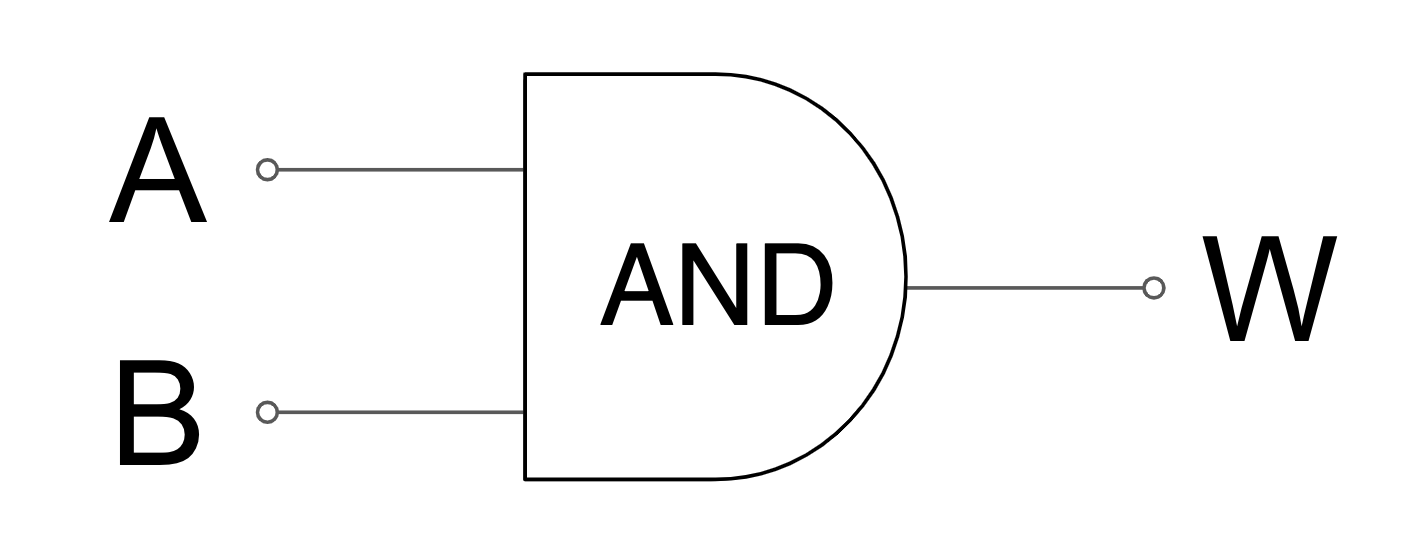
1 Bit Addition

A + B = W X
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

what
about
this?

Introducing XOR

"exclusive or"

XOR

exclusive or

aka

or but not and

A B A XOR B
1 1 0
1 0 1
0 1 1
0 0 0

BinaryArithmetic

 1
+0
01

 0
+1
01

 0
+0
00

 1
+1
10

  A
 +B
 WX
A + B = W X
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

looks like
A XOR B

BinaryArithmetic

A + B = W X
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

looks like
A XOR B

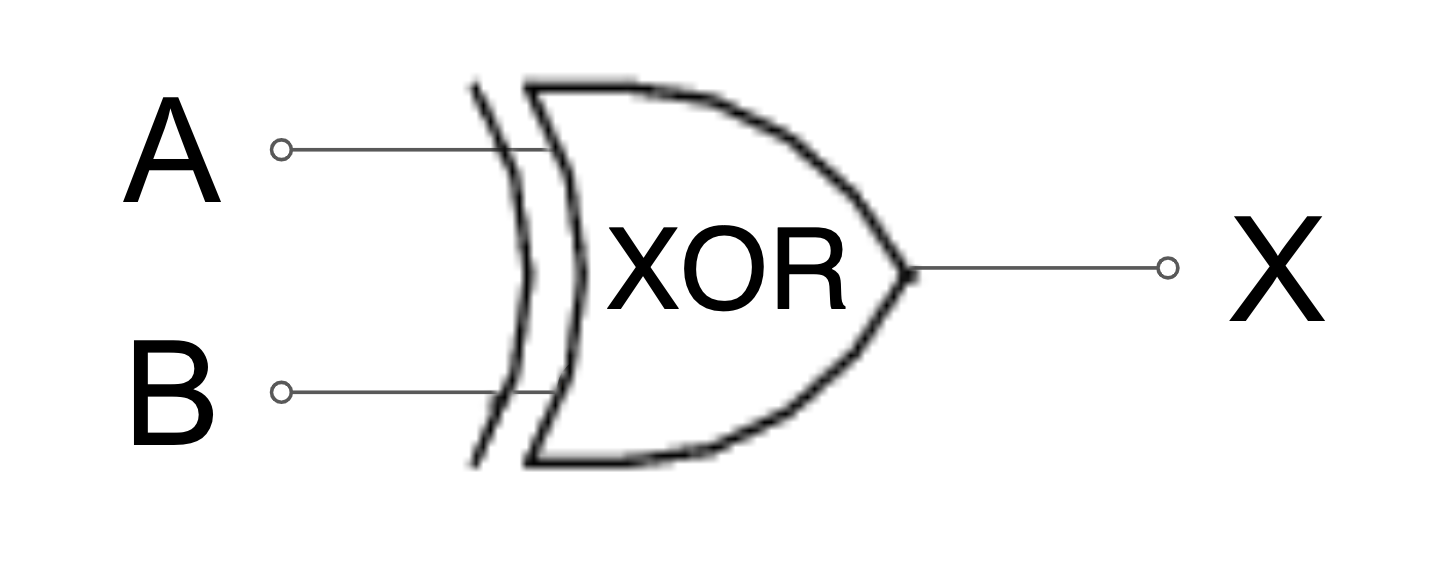
1 Bit Addition with Carry

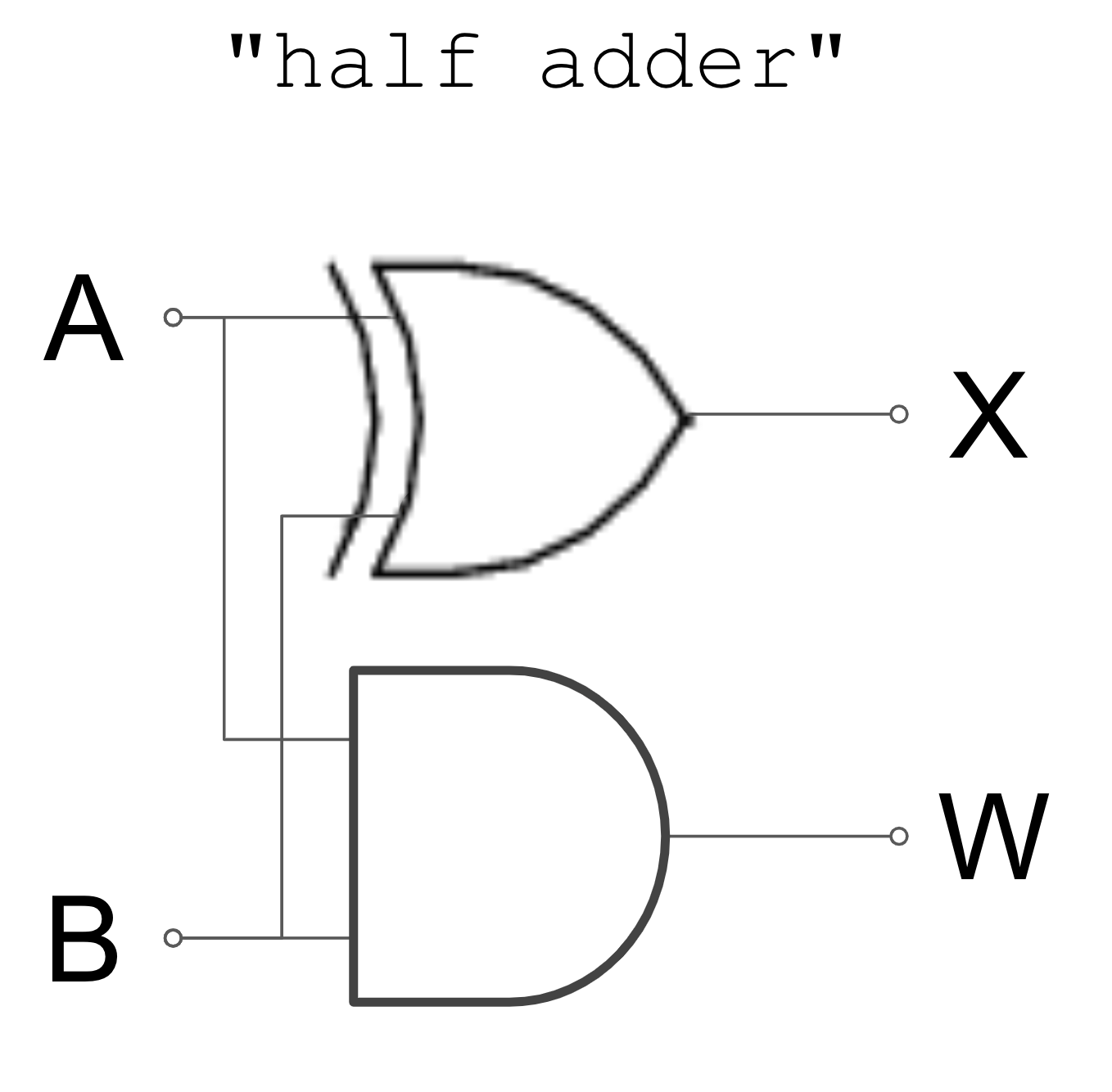
STOP+TRY: build the half adder circuit. Use switches for inputs and bulbs for outputs.

What
about
this?

ab
+cd
wxy

Jump to Logic Reduction

STOP+THINK
What would the truth table look like?

ab
+cd
wxy

ab
+cd
wxy

A B C D W X Y
1 1 1 1 1 1 0
1 1 1
1 1 1
1 1
1 1 1
1 1
1 1
1
0 1 1 1
0 1 1
0 1 1
0 1
0 1 1
0 1
0 1
0

11

+11

110

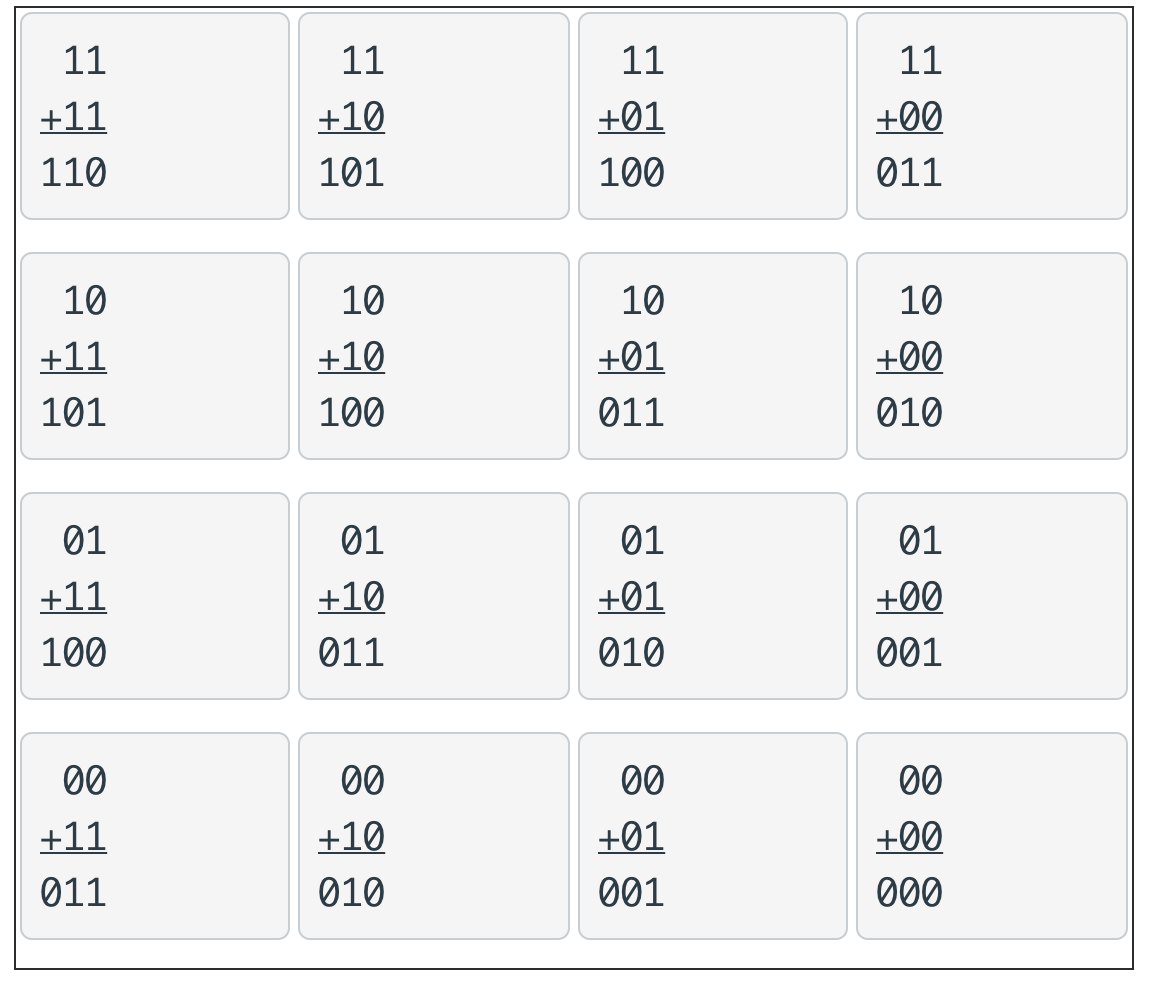
A B C D W X Y
1 1 1 1 1 1 0
1 1 1 0 1 0 1
1 1 0 1 1 0 0
1 1 0 0 0 1 1
1 0 1 1 1 0 1
1 0 1 0 1 0 0
1 0 0 1 0 1 1
1 0 0 0 0 1 0
0 1 1 1 1 0 0
0 1 1 0 0 1 1
0 1 0 1 0 1 0
0 1 0 0 0 0 1
0 0 1 1 0 1 1
0 0 1 0 0 1 0
0 0 0 1 0 0 1
0 0 0 0 0 0 0

When is W true?

ABCD

or

ABC!D

or

AB!CD

or

A!BCD

or

A!BC!D

or

!ABCD

 

A B C D W X Y
1 1 1 1 1 1 0
1 1 1 0 1 0 1
1 1 0 1 1 0 0
1 1 0 0 0 1 1
1 0 1 1 1 0 1
1 0 1 0 1 0 0
1 0 0 1 0 1 1
1 0 0 0 0 1 0
0 1 1 1 1 0 0
0 1 1 0 0 1 1
0 1 0 1 0 1 0
0 1 0 0 0 0 1
0 0 1 1 0 1 1
0 0 1 0 0 1 0
0 0 0 1 0 0 1
0 0 0 0 0 0 0
A B C D W X Y
1 1 1 1 1 1 0
1 1 1 0 1 0 1
1 1 0 1 1 0 0
1 1 0 0 0 1 1
1 0 1 1 1 0 1
1 0 1 0 1 0 0
1 0 0 1 0 1 1
1 0 0 0 0 0 1
0 1 1 1 1 0 0
0 1 1 0 0 1 1
0 1 0 1 0 1 0
0 1 0 0 0 0 1
0 0 1 1 0 1 1
0 0 1 0 0 1 0
0 0 0 1 0 0 1
0 0 0 0 0 0 0

W=ABCD+ABC!D+AB!CD+A!BCD+!ABCD+A!BC!D

We could just build this as a circuit but it would be...complicated.

A B C D W X Y
1 1 1 1 1 1 0
1 1 1 0 1 0 1
1 1 0 1 1 0 0
1 1 0 0 0 1 1
1 0 1 1 1 0 1
1 0 1 0 1 0 0
1 0 0 1 0 1 1
1 0 0 0 0 0 1
0 1 1 1 1 0 0
0 1 1 0 0 1 1
0 1 0 1 0 1 0
0 1 0 0 0 0 1
0 0 1 1 0 1 1
0 0 1 0 0 1 0
0 0 0 1 0 0 1
0 0 0 0 0 0 0

W=ABCD+ABC!D+AB!CD+A!BCD+!ABCD

We wonder if there is a simpler but equivalent version of this expression.

A B C D W X Y
1 1 1 1 1 1 0
1 1 1 0 1 0 1
1 1 0 1 1 0 0
1 1 0 0 0 1 1
1 0 1 1 1 0 1
1 0 1 0 1 0 0
1 0 0 1 0 1 1
1 0 0 0 0 0 1
0 1 1 1 1 0 0
0 1 1 0 0 1 1
0 1 0 1 0 1 0
0 1 0 0 0 0 1
0 0 1 1 0 1 1
0 0 1 0 0 1 0
0 0 0 1 0 0 1
0 0 0 0 0 0 0

W=ABCD+ABC!D+AB!CD+A!BCD+!ABCD

Equivalent means it would have the same truth table.

A B C D W X Y
1 1 1 1 1 1 0
1 1 1 0 1 0 1
1 1 0 1 1 0 0
1 1 0 0 0 1 1
1 0 1 1 1 0 1
1 0 1 0 1 0 0
1 0 0 1 0 1 1
1 0 0 0 0 0 1
0 1 1 1 1 0 0
0 1 1 0 0 1 1
0 1 0 1 0 1 0
0 1 0 0 0 0 1
0 0 1 1 0 1 1
0 0 1 0 0 1 0
0 0 0 1 0 0 1
0 0 0 0 0 0 0

W=ABCD+ABC!D+AB!CD+A!BCD+!ABCD

Simpler means fewer terms and fewer operators.

e.g.

P=ABCD + ABC!D + AB!C + A!B

P=ABC(D+!D) + AB!C + A!B 

P=ABC(TRUE) + AB!C + A!B 

P=ABC + AB!C + A!B 

P=AB(C+!C) + A!B 

P=AB + A!B 

P=A(B+!B)

P=A 

A B C D ABCD ABC!D AB!C A!B P
1 1 1 1 1 1
1 1 1 0 1 1
1 1 0 1 1 1
1 1 0 0 1 1
1 0 1 1 1 1
1 0 1 0 1 1
1 0 0 1 1 1
1 0 0 0 1 1
0 1 1 1
0 1 1 0
0 1 0 1
0 1 0 0
0 0 1 1
0 0 1 0
0 0 0 1
0 0 0 0

Pause

Logic Reduction

AB + A!B = A(B+!B) = A and TRUE = A

 

A may be a compound expression:

PQR + PQ!R = (PQ)(R+!R) = PQ

P=ABCD + ABC!D + AB!C + A!B

ABC(D+!D)

ABC

AB(C+!C)

AB

A(B+!B) 

A

change A

ABCD

A!BCD

ABC!D

AB!CD

!ABCD

change C

change B

change D

A B C D   Y
1 1 1 1   1
1 1 1 0   1
1 1 0 1   1
1 1 0 0   1
1 0 1 1   1
1 0 1 0   0
1 0 0 1   0
1 0 0 0   0
0 1 1 1   1
0 1 1 0   0
0 1 0 1   0
0 1 0 0   0
0 0 1 1   1
0 0 1 0   0
0 0 0 1   0
0 0 0 0   0

 

AB
CD
ABCD
ABC!D
AB!CD
AB!C!D
A!BCD
!ABCD
!A!BCD
ABC
AB!C
ACD
!ACD
CD
00 01 11 10
AB
00
!A!B!C!D
 
!A!B!CD
!A!BCD
!A!BC!D

01
!AB!C!D
 
!AB!CD
!ABCD
!ABC!D

11
AB!C!D
 
AB!CD
ABCD
ABC!D

10
A!B!C!D
 
​A!B!CD
​A!BCD
​A!BC!D

Karnaugh Map

CD
00 01 11 10
AB 00 !A!B!C!D
0		 !A!B!CD1 !A!BCD
3		 !A!BC!D
2
01 !AB!C!D
4		 !AB!CD
5		 !ABCD
7		 !ABC!D
6
11 AB!C!D
12		 AB!CD
13		 ABCD
15		 ABC!D
14
10 A!B!C!D
8		 ​A!B!CD
9		 ​A!BCD
11		 ​A!BC!D
10

Karnaugh Map

CD
00 01 11 10
AB 00
 
 
 
01
 
 
 
 
11 AB!C!D
1		 AB!CD
1		 ABCD
1		 ABC!D
1
10 A!B!C!D
1		 ​A!B!CD
1		 ​A!BCD
1		 ​A!BC!D
1

P=ABCD + ABC!D + AB!CD + A!BCD + AB!C!D +A!B!CD + A!B!C!D + A!BC!D

CD
00 01 11 10
AB 00
 
 
 
01
 
 
 
 
11 AB!C!D
1		 AB!CD
1		 ABCD
1		 ABC!D
1
10 A!B!C!D
1		 ​A!B!CD
1		 ​A!BCD
1		 ​A!BC!D
1

P=ABCD + ABC!D + AB!CD + A!BCD + AB!C!D +A!B!CD + A!B!C!D + A!BC!D

CD
00 01 11 10
AB 00
 
 
 
01
 
 
 
 
11 AB!C!D
1		 AB!CD
1		 ABCD
1		 ABC!D
1
10 A!B!C!D
1		 ​A!B!CD
1		 ​A!BCD
1		 ​A!BC!D
1

P=ABCD + ABC!D + AB!CD + A!BCD + AB!C!D +A!B!CD + A!B!C!D + A!BC!D

CD
00 01 11 10
AB 00





01







11
 		 1 1 1 1
10
 		 1 1 1 1

P=ABCD + ABC!D + AB!C + A!B

P=ABCD + ABC!D + AB!CD + AB!C!D + A!BCD + A!BC!D + A!B!CD + A!B!C!D

Finis

NOTE: X1=B, X3=A, X0=C, X2=D

C is 1 here

D is 1 here

A is 1 here

B is 1 here

KMaps & Race Conditions

A

C

B

D

  1      0  1     1   1    0    1

R=!ABC!D+A!B!C!D+A!B!CD+A!BC!D+A!BCD+AB!C!D+AB!CD+ABC~D

00 01 11 10
00
01 1
11 1 1 1
10 1 1 1 1

AB

CD

A!C

A!B

R=A!B + A!C + BC!D

BC!D

  1      0  1     1   1    0    0
  0      0  1     1   0    0    0
  0      0  1     1   1    0    1
  1      1  1         1    1    1

Race Conditions - the race is among these AND gates. Their inputs depend on A, B, C, and D but some might be delayed by NOT

  0         1         0         0

!A

  0         1         0         0

!B

  0         0         0         0

!C

  1         1         1         0

!D

  1         1         1         1

A

  1         0         1         1

B

  1         1         1         1

C

  0         0         0         0

D

R=A!B + A!C + BC!D

R=A!B + A!C + BC!D + A!D

Logic

By Dan Ryan

Logic

  • 554

More from Dan Ryan