Aprendendo dados tabulares com RBMs
Agenda
- Dados tabulares
- Métodos tradicionais
- Máquinas de Boltzmann restritas
- Filtragem colaborativa & RBMs
- Resultados
?
?
?
?
?
?
?
?
Taxonomia dos métodos
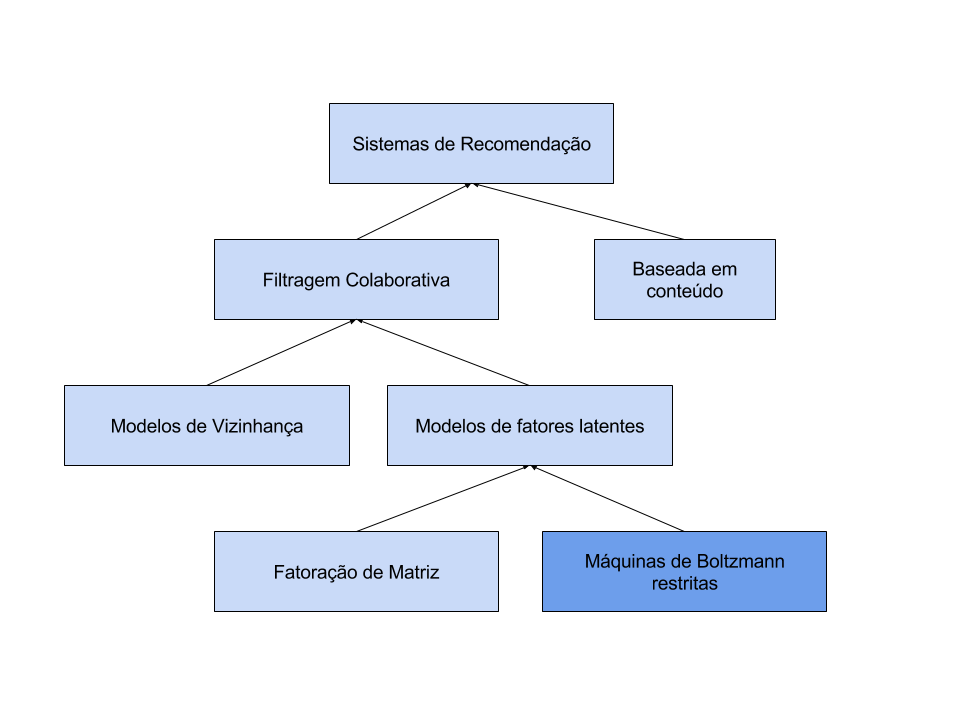
Modelos de Vizinhança
- Descobrir quais usuários compraram itens comuns
- Calcular a similaridade entre esses usuários
- Média de notas x similaridades
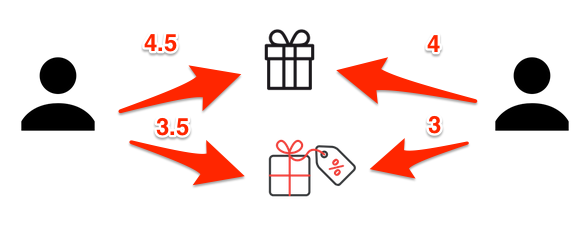
f(
)
f
é a função de similaridade
f(a, u, I) = \frac{\sum_{i \in I} (r_{a,i} - \overline{r_a}) (r_{u,i} - \overline{r_u})}{\sqrt{\sum_{i \in I} (r_{a,i} - \overline{r_a})^{2} \sum_{i \in I}(r_{u,i} - \overline{r_u})^{2}}}
Correlação de Pearson
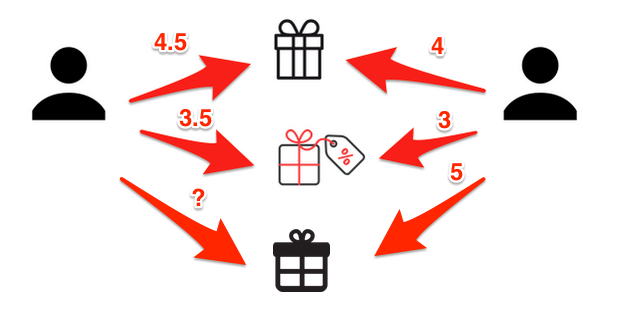
Predição
p_{a,i} = \overline{r_{a}} + \frac{\sum_{u \in K}(r_{u,i} - \overline{r_{u}}) \times w_{a,u}}{\sum_{u \in K} w_{a,u}}
Predição
Modelos de fatores latentes
- Fatores latentes
- Redução de dimensionalidade
- Fatoração de matriz ou RBM
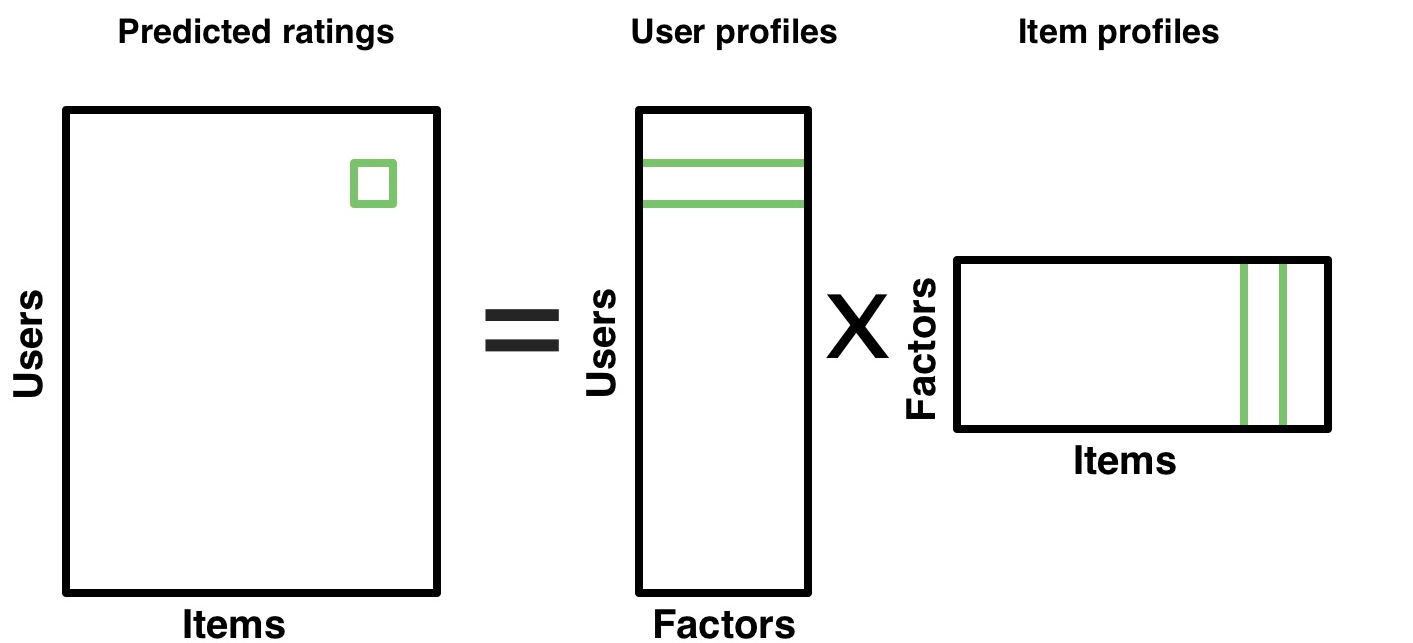
\overline{R}_{(u \times p)} = U_{(u \times k)}P_{(k \times p)}
Fatoração de Matriz
Aprendizado
\text{min} \sum_{i,j \in L}(r_{i,j} - u_{i}p_{j})^2
+ \lambda \left(\sum_{i} n_{u_i} \left \vert\vert u_i \right \vert\vert^2 + \sum_{j} n_{v_j} \vert\vert v_j \vert\vert^2 \right)
RBMs
O que faz?
Características
Treinamento

Dataset



Características
- Generativo
- Baseado em Energias
- Estocástico
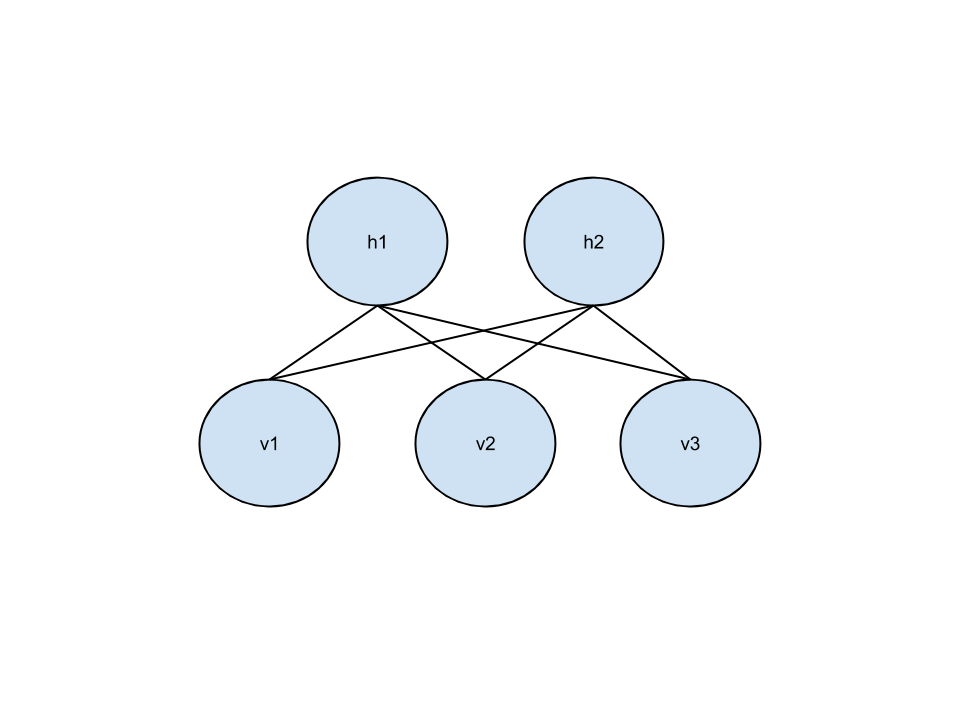
Visible
Hidden
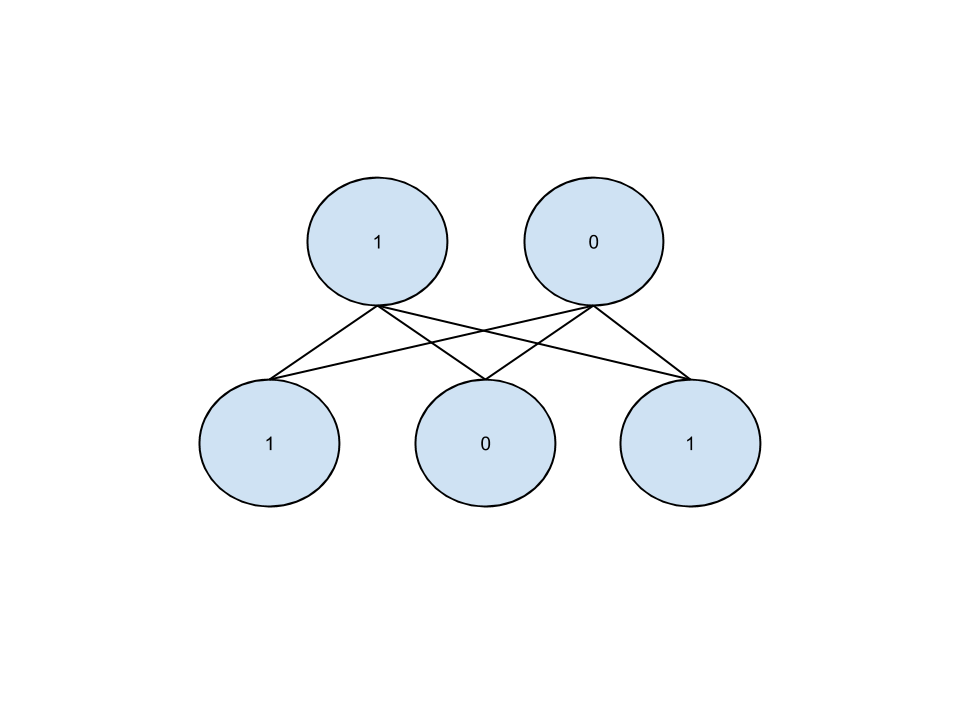
Energia
E(v, h) = -\sum \limits_{i} b_i v_i - \sum \limits_{j} c_j h_j - \sum \limits_{i} \sum \limits_{j} v_i w_{ij} h_j
Probabilidade de uma configuração
P(v, h) = \frac{e^{-E(v, h)}}{Z}
Probabilidade marginal de uma entrada
P(v) = \frac{1}{Z} \sum \limits_{h} e^{-E(v, h)}
Probabilidades condicionais
P(v|h) = \prod \limits_{i=1}^m P(v_i|h)
P(h|v) = \prod \limits_{j=1}^n P(h_j|v)
Aprendizado
\arg\min \limits_{W} \mathbb{E} \left[\sum \limits_{v \in V} - \log P(v)\right]
Derivada e correção
\frac{\partial \log P(v)}{w_{ij}} = \langle\ v_i h_j \rangle_{data} - \langle\ v_i h_j \rangle_{model}
\Delta w_{ij} = \epsilon(\langle\ v_i h_j \rangle_{data} - \langle\ v_i h_j \rangle_{model})

x = \{1, 0, 1\}
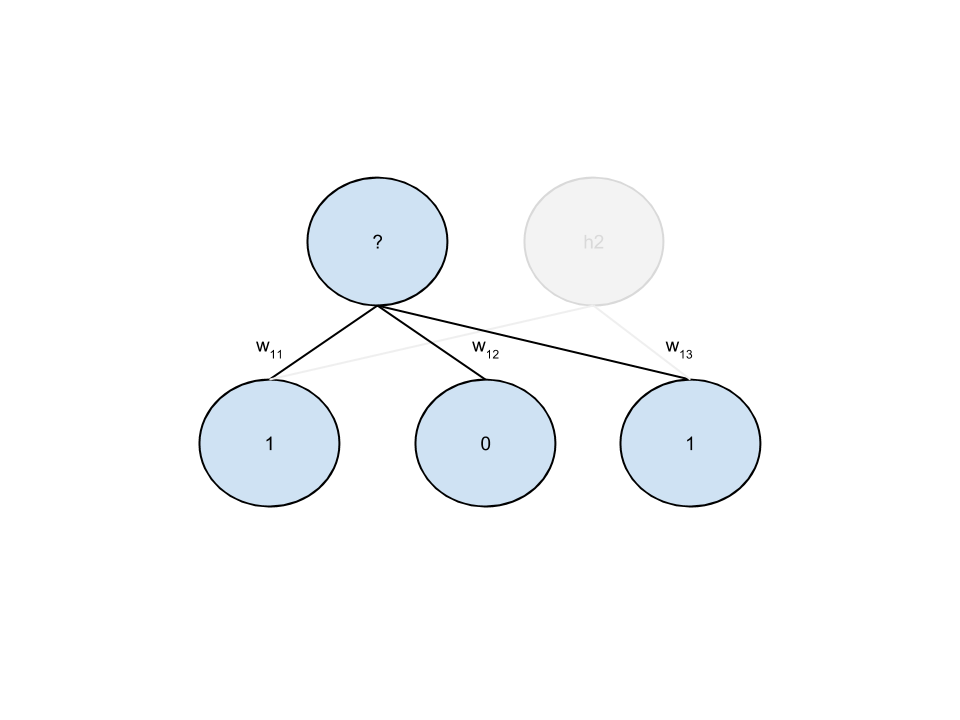
P(h_j=1|v) = \sigma \left(c_j + \sum_{i=1}^m w_{i,j} v_i \right)
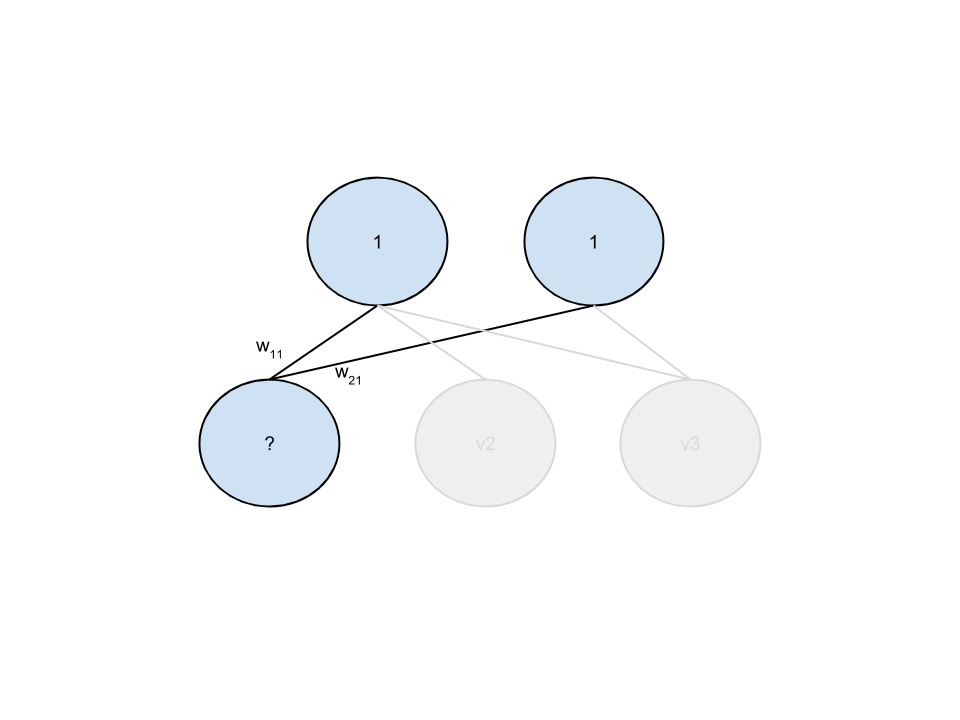
P(v_i=1|h) = \sigma \left(a_i + \sum_{j=1}^n w_{i,j} h_j \right)
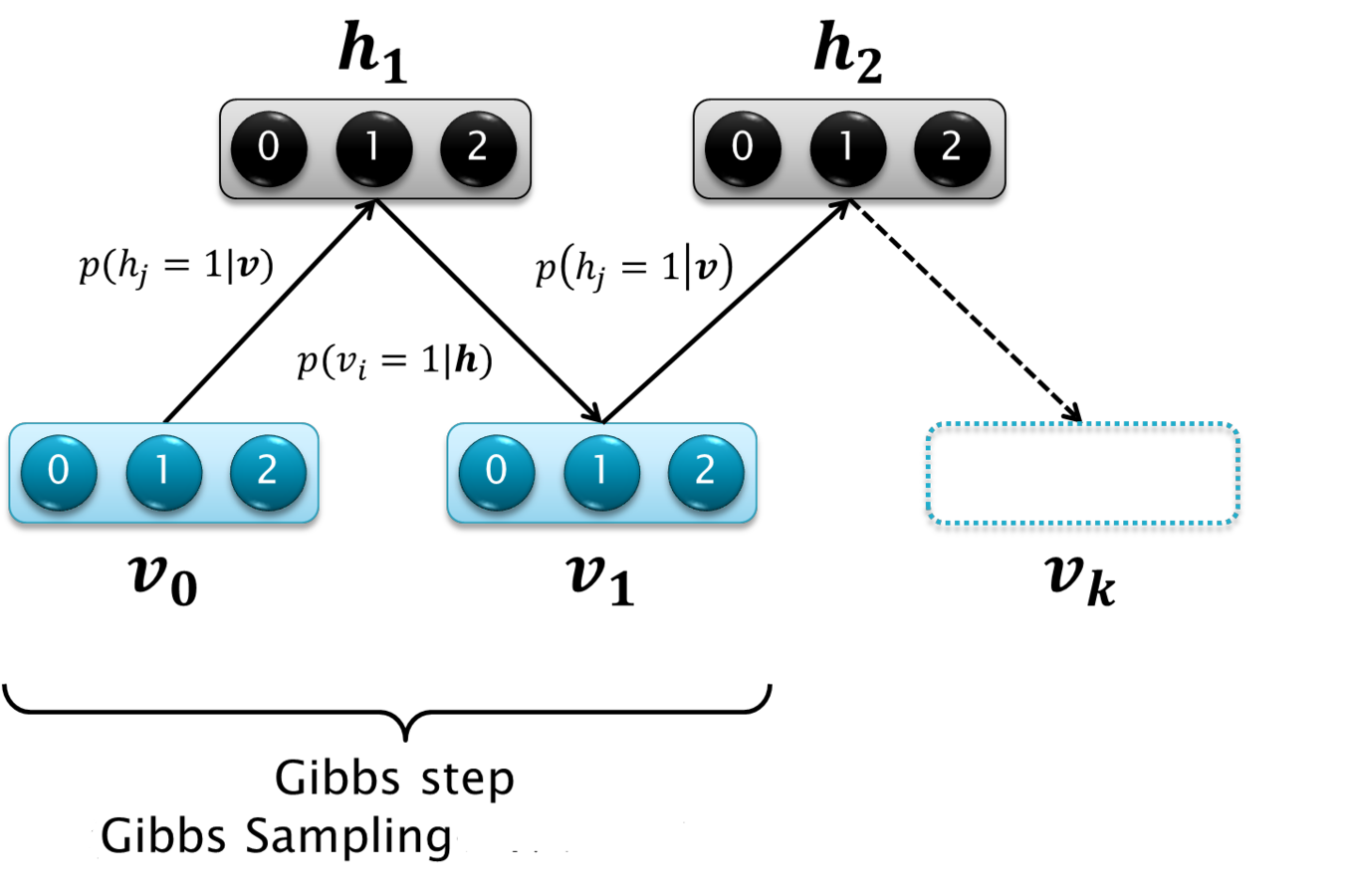
v_0 = \{1, 0, 1\}
v_1 = \{1, 1, 1\}
CD-k
k = passos de amostragem
FC & RBMs
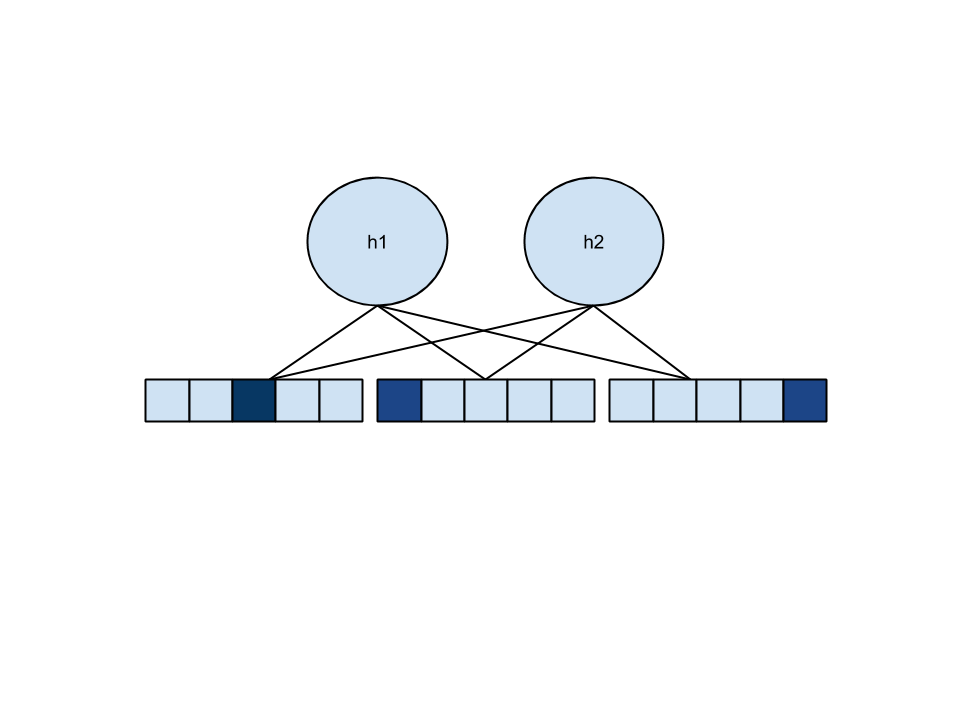
Item 1
Item 2
Item 3
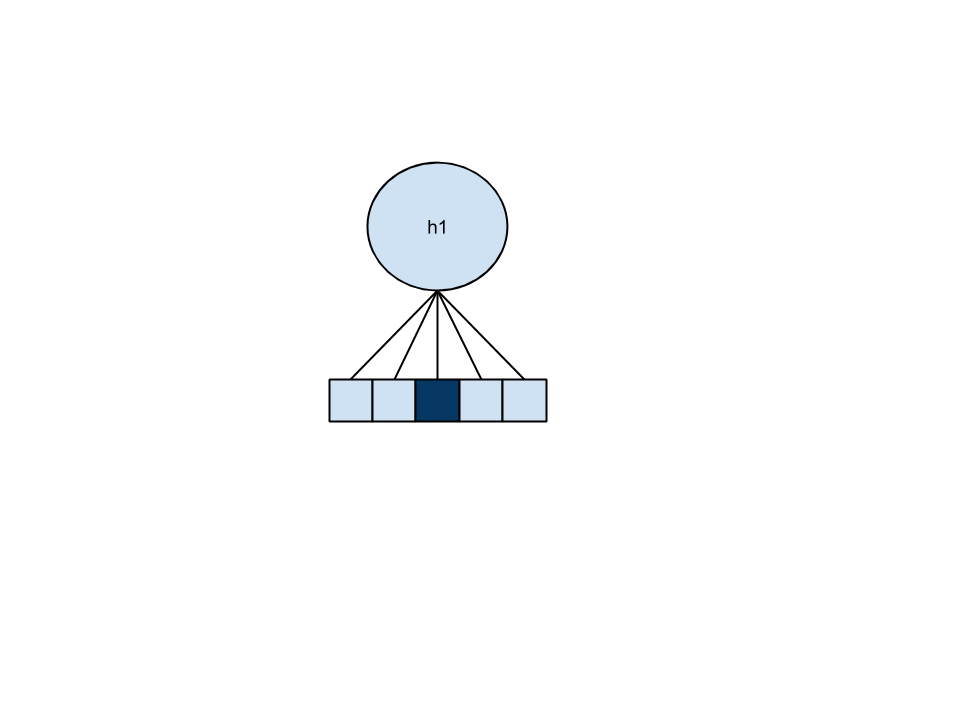
Em detalhe
- nós binários, um pra cada nota
- Um peso e um viés de entrada para cada nota de 1 a
k
k
Ativação de uma unidade visível
P(v_i^k = 1|h) = \frac{\exp(b_i^k + \Sigma_j W_{ij}^k h_j)} {\Sigma_{k=1}^K \exp(b_i^k + \Sigma_j W_{ij}^k h_j)}
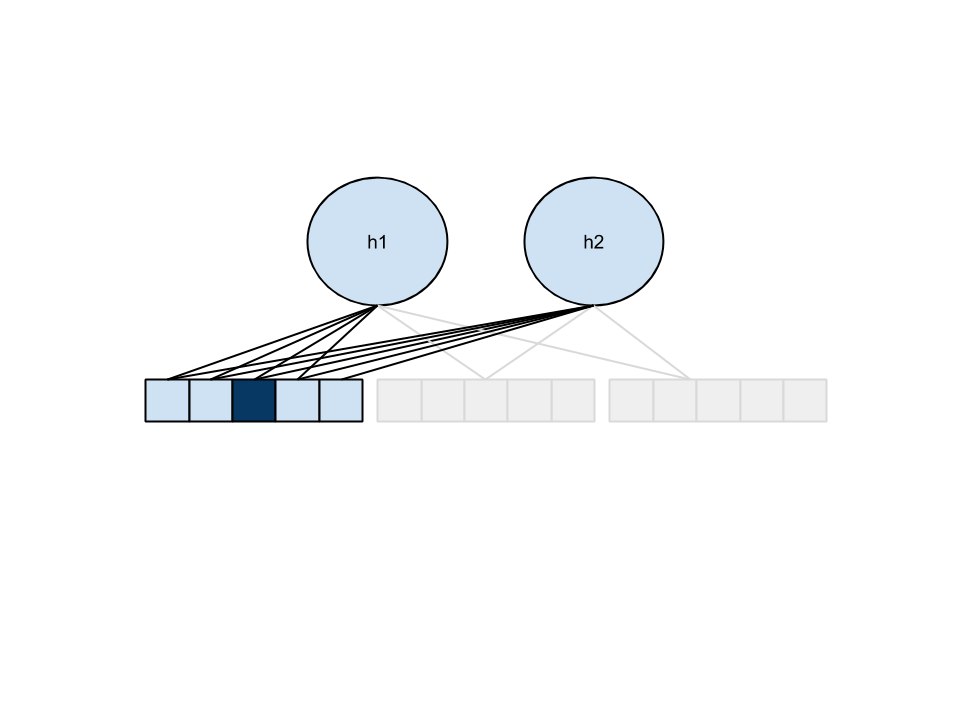
Predição
- Realizar uma etapa de amostragem e escolhe a maior ativação de uma unidade
- Obter energia dos 5 ratings possíveis, normalizar e usar o valor esperado como predição
Experimentos
U-RBM & I-RBM
Validação - H
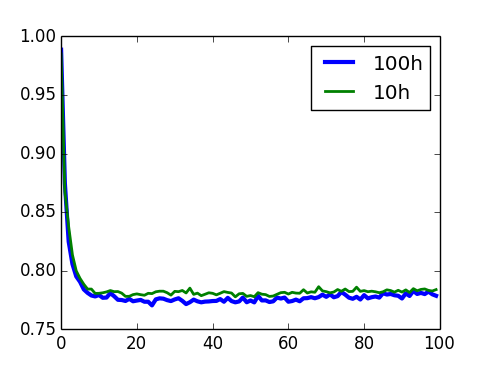
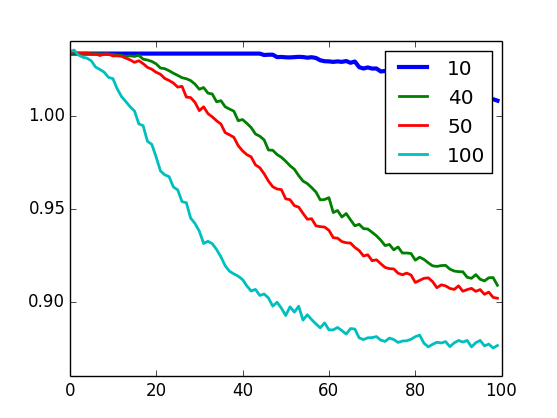
U-RBM
I-RBM
Validação - tx. aprendzado
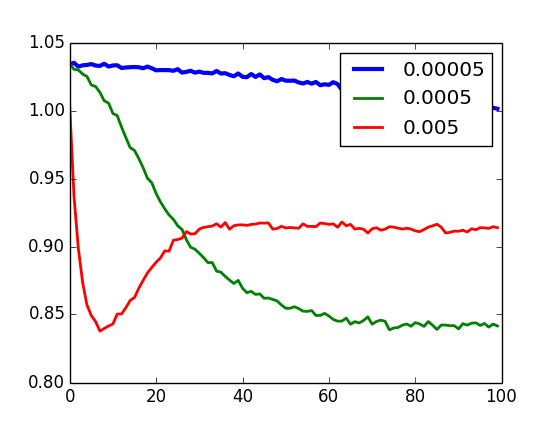
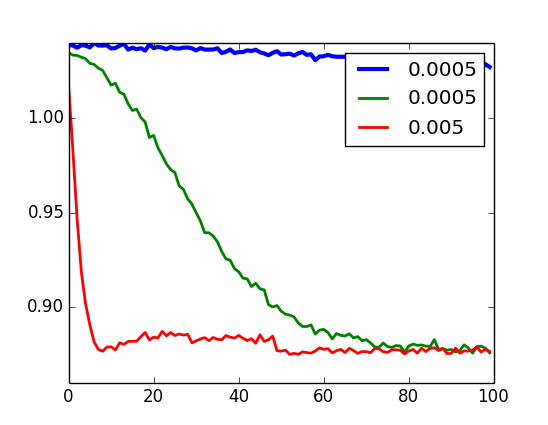
U-RBM
I-RBM
Validação - momentum
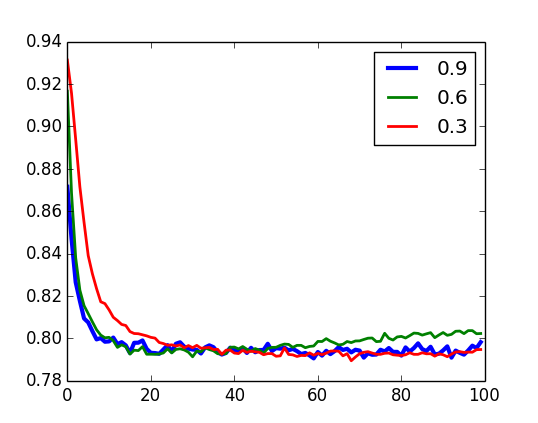
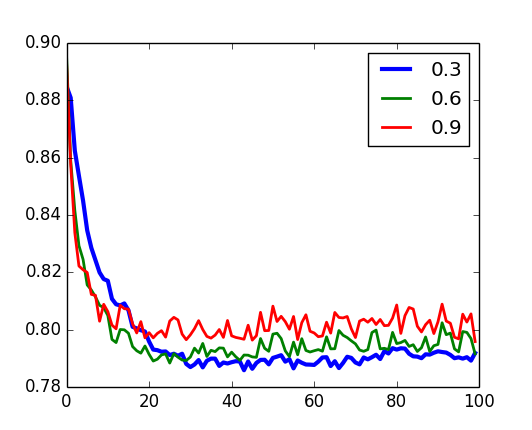
U-RBM
I-RBM
Validação - decaimento
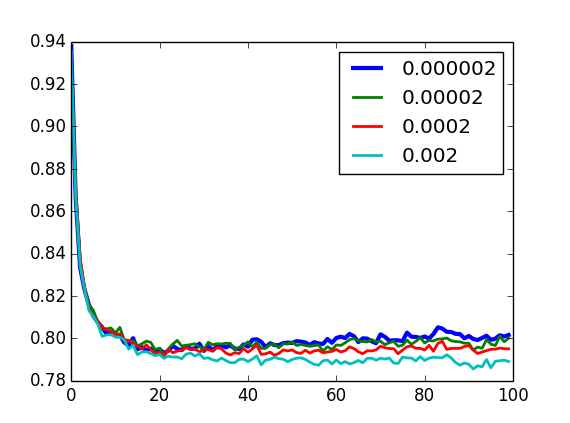
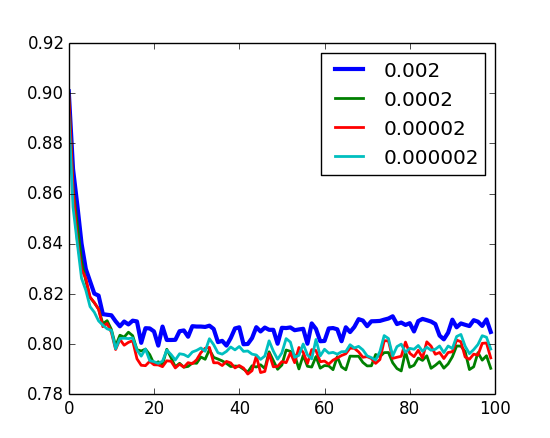
U-RBM
I-RBM
Referências
-
Ruslan Salakhutdinov, Andriy Mnih and Geoffrey Hinton. “Restricted Boltzmann machines for collaborative filtering”. In: In Machine Learning, Proceedings of the Twenty-fourth International Conference (ICML 2004). ACM. AAAI Press, 2007, pp. 791–798.
-
Geoffrey E. Hinton. “A Practical Guide to Training Restricted Boltzmann Machines”. In: Neural Networks: Tricks of the Trade - Second Edition. 2012, pp. 599–619. doi: 10.1007/978-3-642-35289-8_32. url: http: //dx.doi.org/10.1007/978-3-642-35289-8_32.
Fim
Perguntas?
fcruz@inf.puc-rio.br
Aprendendo dados tabulares com RBMs
By Felipe Cruz
Aprendendo dados tabulares com RBMs
RBMs & FC
- 707



