Recommendation Algorithms
Felipe Cruz
@felipejcruz
github.com/felipecruz
Problem
Algorithms
CF & RBMs
Motivation
relevance
efficiency
personalization
?
Problem
?
?
?
?
?
?
?
?
+
=
?
How many users?
How many products?
Recommendation is not only for "big data"
....
but "big data" implies more resources
Problem
AlgorithmsCF & RBMs
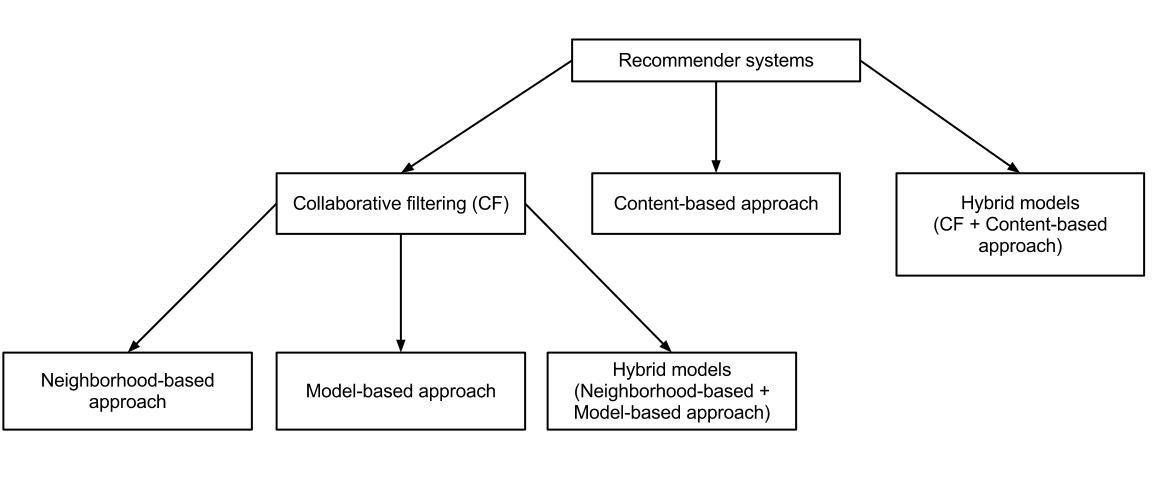
Recommender systems
Recommender systems
Collaborative Filtering
Similarity
(neighborhood based)
Training
For each user
Find users that purchased common items
Training
Training
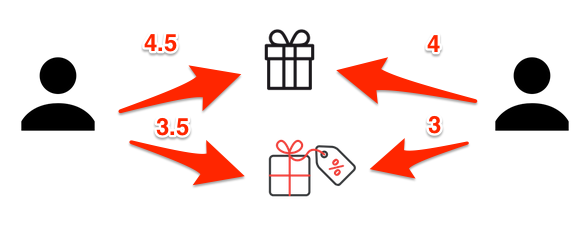
now we can measure similarity
f(
)
f
is the similarity function
f(a, u, I) = \frac{\sum_{i \in I} (r_{a,i} - \overline{r_a}) (r_{u,i} - \overline{r_u})}{\sqrt{\sum_{i \in I} (r_{a,i} - \overline{r_a})^{2} \sum_{i \in I}(r_{u,i} - \overline{r_u})^{2}}}
Pearson correlation
rating given by user a to item i less the average rating by user a
I = \{ \quad , \quad \}
\sum_{i \in I} (r_{a,i} - \overline{r_a})
(r_{u,i} - \overline{r_u})
\sum_{i \in I} (r_{a,i} - \overline{r_a})
(r_{u,i} - \overline{r_u})
[(4.5 - 4)(4 - 3.5)] + [(3.5 - 4)(3 - 3.5)]
[0.5 \times 0.5]+[-0.5 \times -0.5] = 0.5
\sqrt{\sum_{i \in I} (r_{a,i} - \overline{r_a})^2 \sum_{i \in I} (r_{u,i} - \overline{r_u})^2}
[(4.5 - 4)^2 + (3.5 - 4)^2] \times [(4 - 3.5)^2 + (3 - 3.5)^2]
[(0.5)^2 + (-0.5)^2] \times [(0.5)^2 + (-0.5)^2] = \sqrt{0.5^2} = 0.5
\frac{0.5}{0.5} = 1
Prediction ?
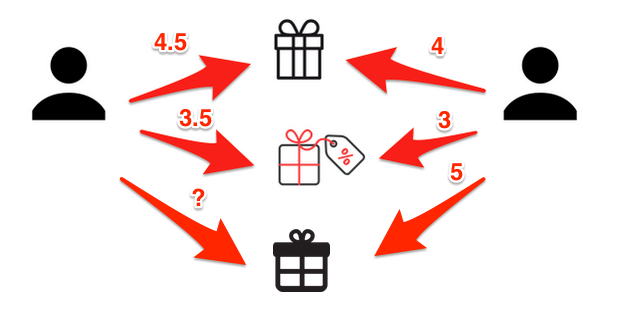
p_{a,i} = \overline{r_{a}} + \frac{\sum_{u \in K}(r_{u,i} - \overline{r_{u}}) \times w_{a,u}}{\sum_{u \in K} w_{a,u}}
Prediction
p_{a,i} = 4 + \frac{5 - 3.5 \times 1}{1} = 5.5
Prediction
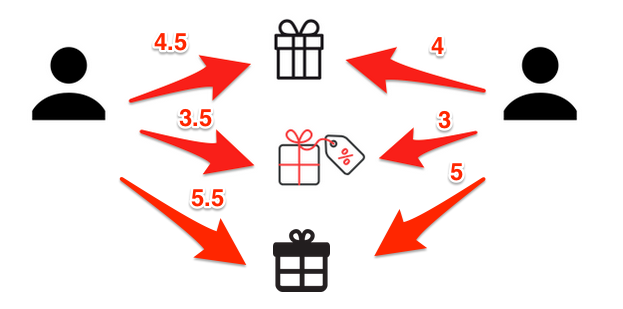
Template method - train
- for u in usuarios:
- similar = same_products(R, u)
- for s in similar:
- S[(u,s)] = similarity(u, s)
Other similarity measures
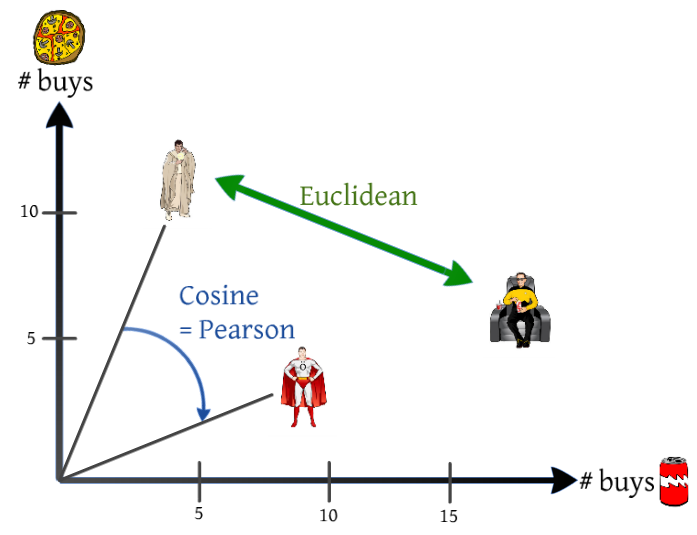
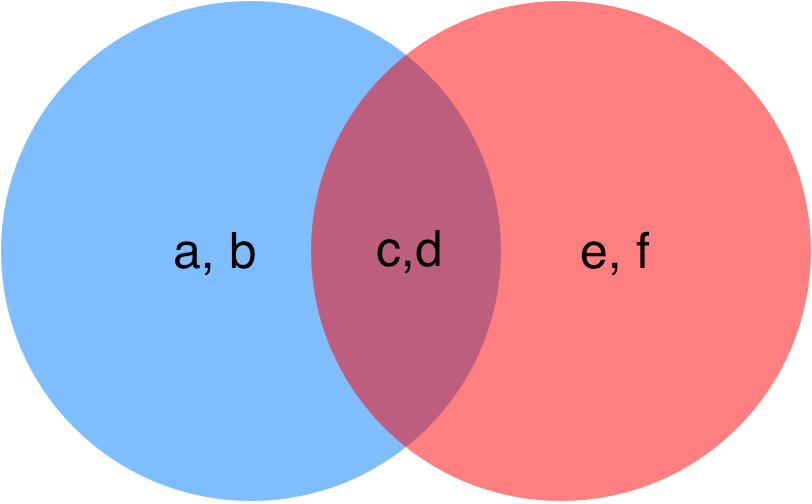
Jaccard
pausa...
Latent factor
(model based)
Capture implicit information
Capture implicity information
#comofaz
?
?
?
?
?
?
?
?
R_{ij} \in
(u \times p)
Let's give a name to that matrix
Model Based?
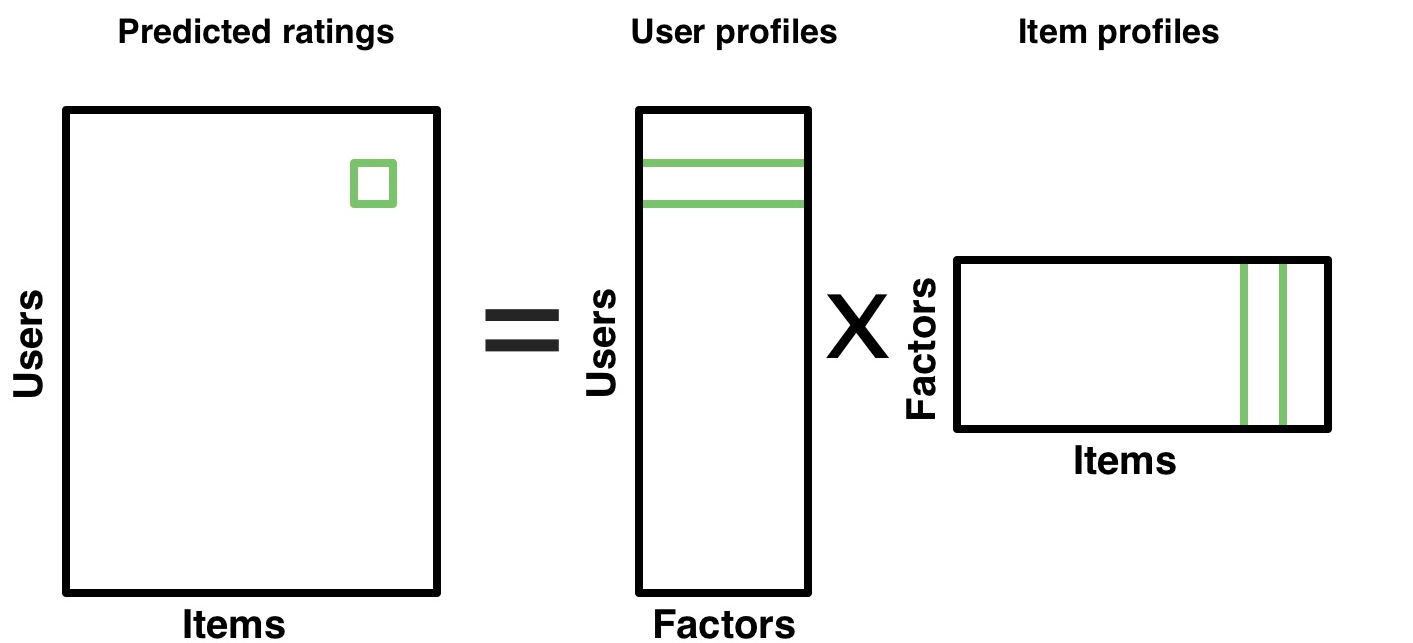
Model
\langle u_{i},p_{j} \rangle \approx R_{ij}
Matrix factorization
\overline{R}_{(u \times p)} = U_{(u \times k)}P_{(k \times p)}
\text{min} \sum_{i,j \in L}(r_{i,j} - u_{i}p_{j})^2
U,P
T
+ \lambda \left(\sum_{i} n_{u_i} \left \vert\vert u_i \right \vert\vert ^2 + \sum_{j} n_{v_j} \vert\vert v_j \vert\vert^2 \right)
Formal problem
\langle u_{i},p_{j} \rangle
\text{min} \sum_{i,j \in L}(r_{i,j} - u_{i}p_{j})^2
U,P
T
+ \lambda \left(\sum_{i} n_{u_i} \left \vert\vert u_i \right \vert\vert^2 + \sum_{j} n_{v_j} \vert\vert v_j \vert\vert^2 \right)
Formal problem
regularization to prevent overfit
\text{min} \sum_{i,j \in L}(r_{i,j} - u_{i}p_{j})^2
U,P
T
E =
\left( \begin{array}{cc}
2 & 4 \\
3 & 6 \end{array} \right)
-
\left( \begin{array}{cc}
\langle u_{1},p_{1} \rangle & \langle u_{1},p_{2} \rangle \\
\langle u_{2},p_{1} \rangle & \langle u_{2},p_{2} \rangle \end{array} \right)
Minimize the error
R_{ij}
\overline{R}_{ij}
ALS Algorithm
- Initialize U with random values
- Fix U, for each line in P we solve a least squares problem to find best values for P
- Fix P, for each line in P we solve a least squares problem to find best values for U
ALS
Fix here
Fix there
Fix here
Fix there
...
Finished!
Problem
AlgorithmsCF & RBMs
RBM
- Generative models
- Pattern recognition
- Efficient learning algorithm
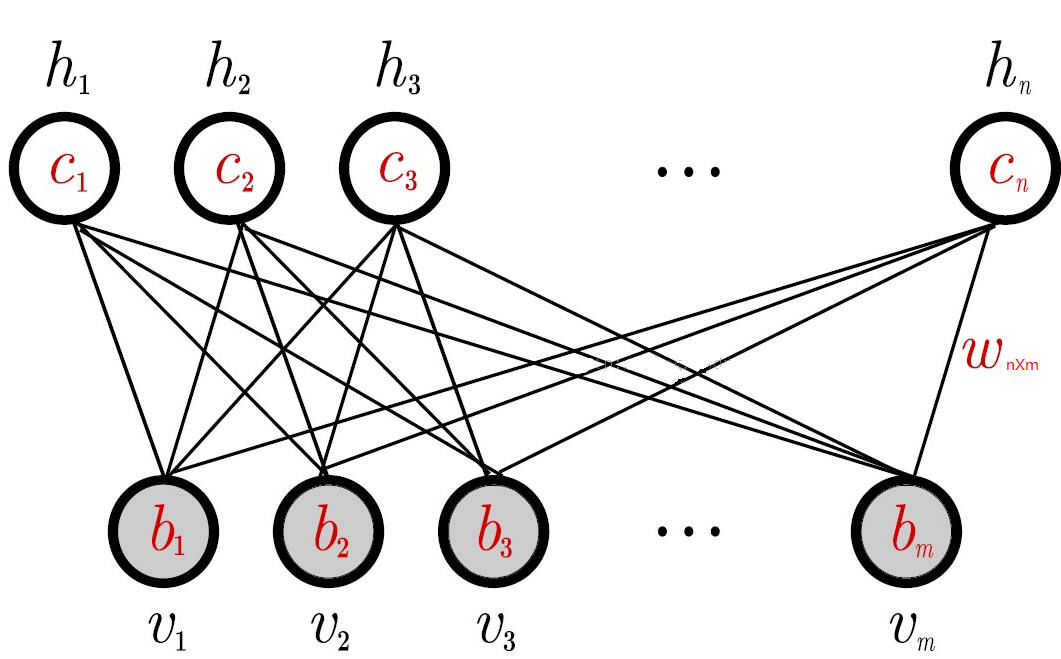
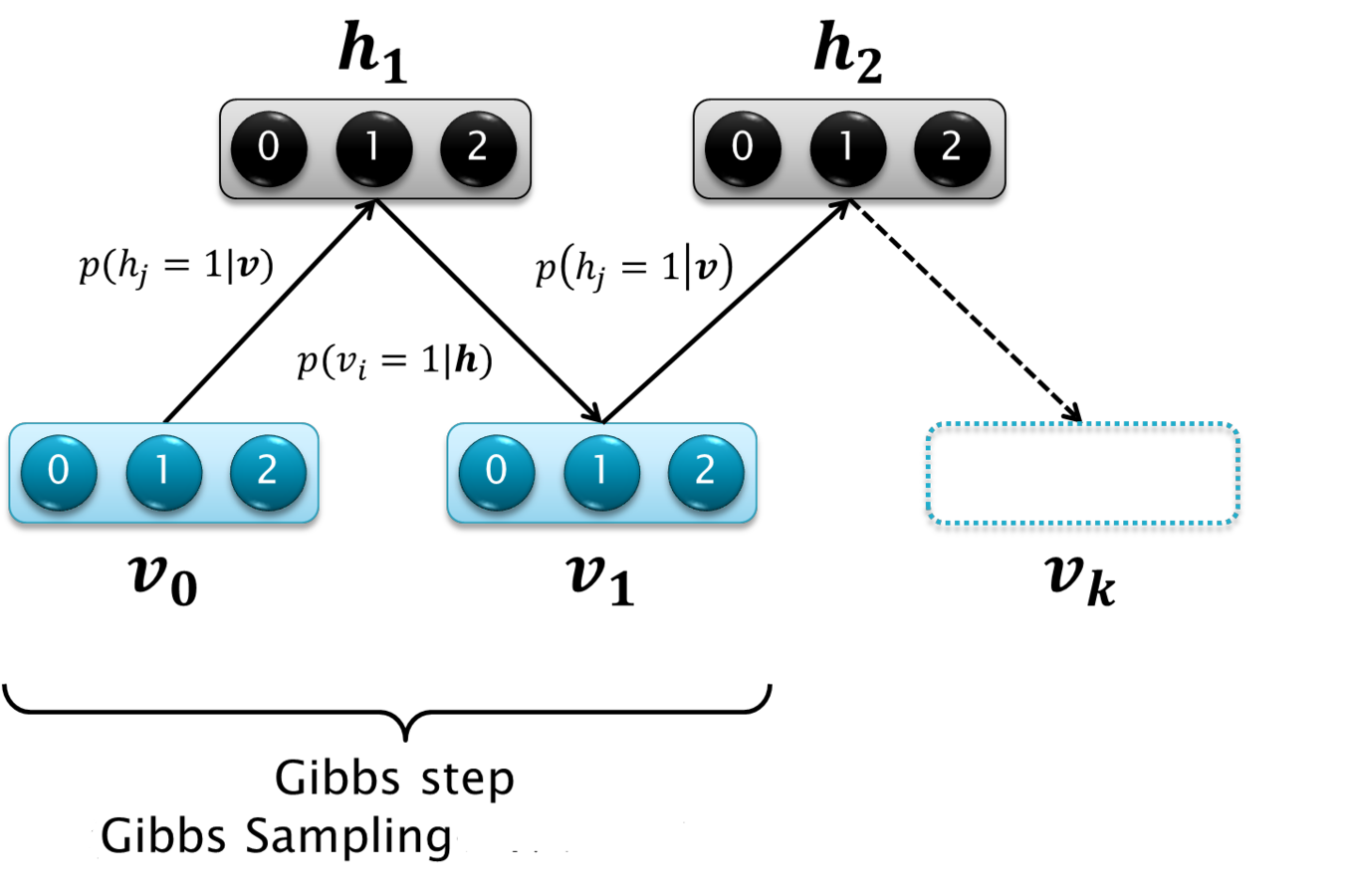
RBMs & CF
Model
- Each product is a binary feature
- 1 if purchased
- 0 if not purchased
It's also possible to use many other binary features
Prediction - input
profile = [0, 0, 0, 1, 0, 0, 0, 1]
(buzios e ilha grande)
Prediction - output
pred = [0, 1, 0, 1, 0, 0, 1, 1]
(buzios, ilha grande, angra, balneário camboriú)
RBM
ALS
In practice
- Works well with dataset samples
- Empty profiles return popular products
- Non deterministic output
- Can be used before a standard algorithm to filter (user, item) tuples for prediction
- Ensembles
http://www.slideshare.net/akyrola/largescale-recommendation-systems-on-just-a-pc
Questions?
@felipejcruz
github.com/felipecruz
Recommendation - Collaborative Filtering techniques
By Felipe Cruz
